- Social Sciences

Mathematics Improves Your Critical Thinking and Problem-Solving Abilities
- Author: Christopher Wanamaker

By studying math, you can become better at solving problems in everyday life.
Rido via Canva Pro
Advantages of Studying Math
Critical thinking, problem-solving, and mathematics are interconnected concepts that can play an important role in our daily lives. Critical thinking is analyzing, evaluating, and examining information to make informed decisions. Problem-solving involves utilizing critical thinking based on knowledge and information from your collective experiences to identify, analyze, and solve complex problems.
Mathematics provides a systematic and logical framework for problem-solving and critical thinking. The study of math helps to develop analytical skills, logical reasoning, and problem-solving abilities that can be applied to many areas of life . By using critical thinking skills to solve math problems, we can develop a deeper understanding of concepts, enhance our problem-solving skills, and improve our ability to make informed decisions in our personal and professional lives.
Several principles that govern how numbers are dealt with are rooted deep in mathematical axioms. These axioms include fundamental principles of logic and reason and form a framework that ensures that conclusions and results are consistent and can be interpreted universally. From this platform, we have discovered the techniques of inductive, deductive, and abductive reasoning, as well as the power of estimation to help hone our ability to learn and understand the world.

Ekaterina Bolovtsova via Pexels
What Is Inductive Reasoning?
Inductive reasoning is a type of reasoning that involves using specific observations or evidence to draw general conclusions or make predictions. It is often used in scientific research and empirical investigations, where data is collected through observation and experimentation. Inductive reasoning involves moving from specific examples to a generalization or hypothesis based on patterns or trends observed in a set of data (Bradford, 2023).
The strength of inductive reasoning lies in its ability to generate new knowledge and hypotheses, but it also comes with some limitations. Inductive reasoning is subject to bias, as the observations and data collected may not be representative of the entire population. Therefore, inductive reasoning often requires further testing and confirmation before a conclusion can be established with any level of certainty.
An example of inductive reasoning is concluding that a specific restaurant is making you sick because every time you eat there, you feel sick afterwards. Using inductive reasoning, you can draw a general conclusion that the food from this specific restaurant is causing your sickness. However, further investigation that rules out other potential causes would be needed to confirm your theory, as there may be other factors causing the sickness.
While the instances of getting sick are correlated in this example, they may not necessarily be directly related. For instance, there may be environmental factors or other things, such as a routine/habit that you partake in before or after eating at the restaurant, that is the real reason you are getting sick.
Correlation Does Not Equal Causation
We have to remember that correlation does not always equal causation. Just because you observe that two variables are correlated does not mean that one caused the other. For example, the average height of professional basketball player is 6’ 6” (Andy, 2022) whereas the average height of the general population in the USA is 5’ 9” (Martinez, 2022). Should we then conclude that playing basketball makes people taller? No, this is obviously incorrect. There are many other examples where data can be correlated (i.e. associated) but no direct relationship between the variables exists.
Falsification of Inductive Reasoning by Counterexamples
It is often the case that a conclusion formed by inductive reasoning is only good for a specific situation or a specific range of circumstance. When testing a conjecture to see if it is true, it is helpful to look for a counterexample that would disprove your hypothesis. If a counterexample is found, then your conclusion found by inductive reasoning is false. However, if a counterexample cannot be found, this does not mean that the conclusion is true.
For example, in mathematics the Riemann Hypothesis is one of the most famous and important unsolved problems. This hypothesis was first proposed by the German mathematician Bernhard Riemann in 1859 and is concerned with the distribution of prime numbers. Prime numbers are numbers that are only divisible by 1 and themselves. As of this writing, the hypothesis has not been proven or to be true or untrue even though mathematicians have been trying to solve the problem for decades. Since finding a proof is extremely difficult, most mathematicians have tried to falsify the hypothesis by finding a counterexample (Sarnak, 2005). Finding even just a single counterexample would prove the Riemann Hypothesis false.

Monstera via Pexels
What Is Deductive Reasoning?
Deductive reasoning is a type of logical disposition that uses general principles, assumptions, and ideas to reach a specific conclusion by using logical rules and inference techniques. This type of logic is most often used in mathematics and philosophy; however, it does have applications in science, legal proceedings, and everyday life as well. The goal of deductive reasoning is to establish the truth or legitimacy of a hypothesis (Bradford, 2023).
The strength of deductive reasoning lies in its ability to establish the validity of a conclusion, as long as the assumptions are true and the logical basis is solid. However, if your assumptions are flawed or false or your logical foundation is weak, then the conclusion would also be false. In the field of mathematics, written proofs are created by taking general principles and making a specific claim via the process of deductive reasoning.
An example of deductive reasoning is concluding that an apple is a fruit when you have made the assumption that all fruits have seeds and that apples have seeds. In this example, the first assumption establishes a general principle that all fruits have seeds. The second assumption identifies that apples have seeds. Using deductive reasoning, we can draw the specific conclusion that an apple is a fruit. This conclusion is valid, as it follows logically from the two assumptions. Of course, this is an overly simplified case.
Recommended

Wellington House: Britain's WW1 Propaganda Bureau
Utilizing deductive reasoning in ordinary life can make it easier to make decisions or solve problems. In many cases, we often naturally follow the logical steps of deductive reasoning without even thinking about it. For example, if you are trying to decide on whether or not to go on a vacation, we can conclude that we should go if the following 3 assumptions are true:
- I have extra money budgeted for vacations
- I can get the time off of work
- My family wants to go
By understanding how deductive reasoning works, we can be more deliberate about making decisions and solving problems in our lives.

Diego PH via UnSplash
What Is Abductive Reasoning?
A third type of reasoning is called abductive reasoning. Abductive reasoning is a method whereby a theory or hypothesis is formed from an incomplete set of data or circumstances. People that employ this method of reasoning are usually making an educated guess about a situation based on looking at the most likely solution to a problem (Bradford, 2023). Doctors often use abductive reasoning methods in their jobs to diagnose patients. For example, after reviewing symptoms, test results, environmental factors, etc, a doctor may diagnose a patient with the most likely ailment that fits the description.
Occam’s Razor is a kind of abductive reasoning which states that when there are multiple explanations for a problem, the simplest explanation is often most likely the to be true (Andersen-Wood, 2023). Occam’s Razor is a sort of test that scientists sometimes use to help them form a hypothesis to explain a phenomena when there are multiple potential explanations and limited data.
Using the Power of Estimation to Solve Problems
In many cases, solving a complex problem is extremely difficult or time consuming. This is why it is sometimes helpful to use estimation techniques to arrive at a “ball park” answer before you proceed down a specific path to find a solution. Estimation can be especially useful when precision is not required, when time is limited, or when you need to quickly check the reasonableness of an answer. In math, one of the easiest ways to estimate something is to round the numbers up or down before performing mathematical operations. This will give you an estimate of the answer that is obtained more quickly than by solving the problem directly.
Estimation can help you make sense of things in many every-day situations and can be used to form the basis of generalized conclusions. For example, when going on trip you can calculate the total cost of fuel by dividing the distance of your trip by the fuel consumption of your vehicle and then multiplying by the cost of fuel at each fill up. However, it would be much easier and faster to estimate the cost by using average or rounded numbers. This is because the total actual cost when planning a trip will vary depending on fuel prices at each fill-up as well as driving conditions, and driving behaviors. In this example, the estimated cost of fuel should give you a good starting point when planning a trip.
Conclusions
The ability to think critically about any topic is one aspect of what makes us fundamentally human. Moreover, utilizing critical thinking tools such as inductive & deductive reasoning as well as abductive reasoning and estimating techniques can help us to improve our problem solving abilities. The study of math can improve both our ability to problem solve as well as think critically because the foundations of math is rooted in pure logic, reason, and exactness. Therefore, it follows that practicing math can help a person become better at thinking critically about and solving the problems of everyday life.
References and Resources
Andersen-Wood, Frankie. “ What is Occam’s Razor? ” Conceptually . March 6, 2023. <https://conceptually.org/concepts/occams-razor>
Andy. “ The Average Height of NBA Players From 1952-2022 .” The Hoops Geek . July 4, 2022. <https://www.thehoopsgeek.com/average-nba-height/>
Bradford, Alina, & Weisberger, Mindy. “ Deductive Reasoning vs. Inductive Reasoning ” LiveScience . January 30, 2023. <https://www.livescience.com/21569-deduction-vs-induction.html>
Martinez, Kevin. “ The Average Heights of Men Around the World .” Healthline . March 4, 2022. <https://www.healthline.com/health/average-height-for-men>
Sarnak, Peter. “Problems of the Millennium: The Riemann Hypothesis (2004).” Princeton University & Courant Institute of Math. Sciences. April 18, 2005. <https://www.claymath.org/sites/default/files/sarnak_rh_0.pdf>
This content is accurate and true to the best of the author’s knowledge and is not meant to substitute for formal and individualized advice from a qualified professional.
© 2023 Christopher Wanamaker

How to Solve Basic Algebra Word Problems: 20 Example Problems With Solutions

How Critical Thinking Solves the Problem of Postmodern Biblical Interpretation

Creative Thinking and How to Solve Problems

Practical Applications of Mathematics in Everyday Life

The Importance of Mathematics Education in Global Society

Cat Mathematics: How Many Cats Fit Into the Trunk of a Honda Civic?
Check Out the New Website Shop!

Novels & Picture Books

Anchor Charts

- Critical Thinking
How To Encourage Critical Thinking in Math
By Mary Montero
Share This Post:
- Facebook Share
- Twitter Share
- Pinterest Share
- Email Share

Critical thinking is more than just a buzzword… It’s an essential skill that helps students develop problem-solving abilities and make logical connections between different concepts. By encouraging critical thinking in math, students learn to approach problems more thoughtfully, they learn to analyze and evaluate math concepts, identify patterns and relationships, and explore different strategies for finding the solution. Critical thinking also involves a great deal of persistence. Those are critical life skills!
When you think about it, students are typically asked to solve math problems and find the answer. Showing their work is frequently stressed too, which is important, but not the end. Instead, students need to be able to look at math in different ways in order to truly grasp a complete understanding of math concepts. Mathematics requires logical reasoning, problem-solving, and abstract thinking.

What Does Critical Thinking in Math Look Like?
When I think about critical thinking in math, I focus on:
- Solving problems through logical thinking . Students learn how to break down complex problems, analyze the different parts, and understand how they fit together logically.
- Identifying patterns and making connections. Students learn how to identify patterns across different math concepts, make connections between seemingly unrelated topics, and develop a more in-depth understanding of how math works.
- Evaluating and comparing solutions. Students learn to evaluate which solution is best for a given problem and identify any flaws in their reasoning or others’ reasoning when looking at different solutions
Mathematician Posters
These FREE Marvelous Mathematician posters have been a staple in my classroom for the last 8+ years! I first started using a version from MissMathDork and adapted them for my classroom over the years.

I print, laminate, and add magnetic stickers on the back. At the beginning of the year, I only put one or two up at a time depending on our area of focus. Now, they are all hanging on my board, and I’ll pull out different ones depending on our area of focus. They are so empowering to my mathematicians and help them stay on track!
A Marvelous Mathematician:
- knows that quicker doesn’t mean better
- looks for patterns
- knows mistakes happen and keeps going
- makes sense of the most important details
- embraces challenges and works through frustrations
- uses proper math vocabulary to explain their thinking
- shows their work and models their thinking
- discusses solutions and evaluates reasonableness
- gives context by labeling answers
- applies mathematical knowledge to similar situations
- checks for errors (computational and conceptual)
Critical Thinking Math Activities
Here are a few of my favorite critical thinking activities.
Square Of Numbers
I love to incorporate challenge problems (use Nrich and Openmiddle to get started) because they teach my students so much more than how to solve a math problem. They learn important lessons in teamwork, persistence, resiliency, and growth mindset. We talk about strategies for tackling difficult problems and the importance of not giving up when things get hard.
This square of numbers challenge was a hit!
ALL kids need to feel and learn to embrace challenge. Oftentimes, kids I see have rarely faced an academic challenge. Things have just come easy to them, so when it doesn’t, they can lack strategies that will help them. In fact, they will often give up before they even get started.
I tell them it’s my job to make sure I’m helping them stretch and grow their brain by giving them challenges. They don’t love it at first, but they eventually do!
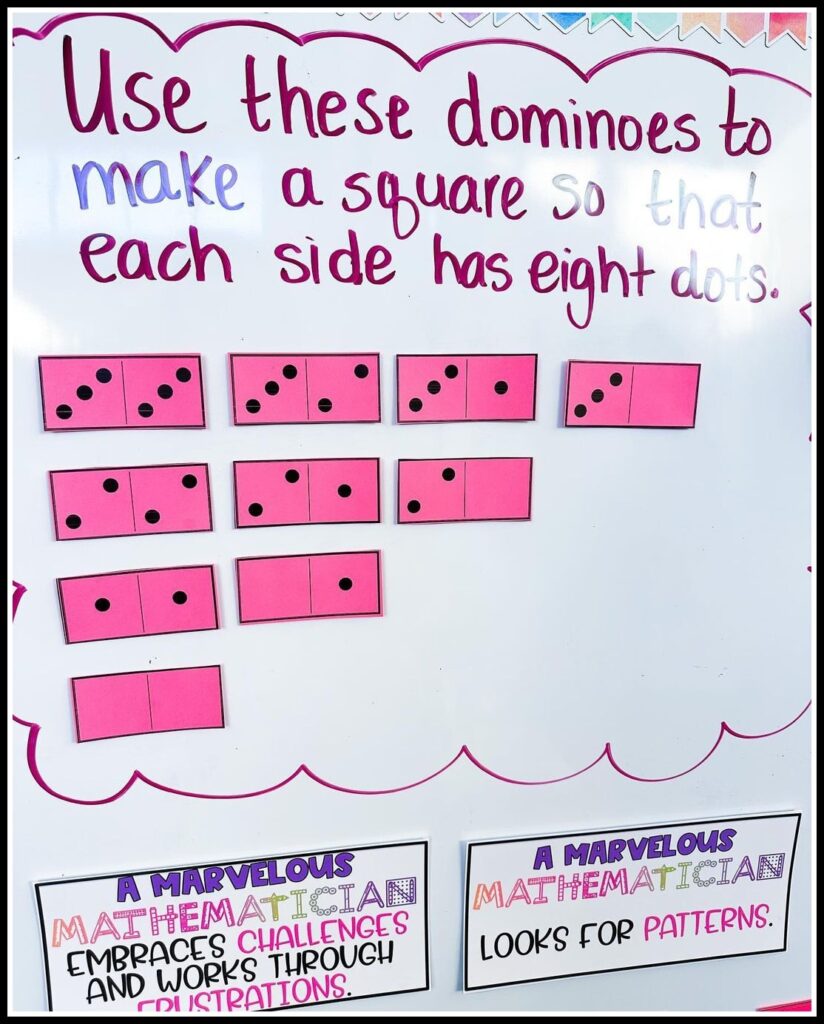
This domino challenge was another one from Nrich . I’m always on the hunt for problems like this!! How would you guide students toward an answer??
Fifteen Cards
This is a well-loved math puzzle with my students, and it’s amazing for encouraging students to consider all options when solving a math problem.

We have number cards 1-15 (one of each number) and only seven are laid out. With the given clues, students need to figure out which seven cards should be put out and in what order. My students love these, and after they’ve done a few, they enjoy creating their own, too! Use products, differences, and quotients to increase the challenge.
This is also adapted from Nrich, which is an AMAZING resource for math enrichment!
This is one of my favorite fraction lessons that I’ve done for years! Huge shout out to Meg from The Teacher Studio for this one. I give each child a slip of paper with this figure and they have to silently write their answer and justification. Then I tally up the answers and have students take a side and DEBATE with their reasoning! It’s an AMAZING conversation, and I highly recommend trying it with your students.
Sometimes we leave it hanging overnight and work on visual models to make some proofs.

Logic Puzzles
Logic puzzles are always a hit too! You can enrich and extend your math lessons with these ‘Math Mystery’ logic puzzles that are the perfect challenge for 4th, 5th, and 6th grades. The puzzles are skills-based, so they integrate well with almost ANY math lesson. You can use them to supplement instruction or challenge your fast-finishers and gifted students… all while encouraging critical thinking about important math skills!

Three levels are included, so they’re perfect to use for differentiation.
- Introductory logic puzzles are great for beginners (4th grade and up!)
- Advanced logic puzzles are great for students needing an extra challenge
- Extra Advanced logic puzzles are perfect for expert solvers… we dare you to figure these puzzles out!
Do you have a group of students who are ready for more of a fraction challenge? My well-loved fraction puzzlers are absolutely perfect for fraction enrichment. They’ll motivate your students to excel at even the most challenging tasks!

Math Projects
Math projects are another way to differentiation while building critical thinking skills. Math projects hold so much learning power with their real-world connections, differentiation options, collaborative learning opportunities, and numerous avenues for cross curricular learning too.
If you’re new to math projects, I shared my best tips and tricks for using math projects in this blog post . They’re perfect for cumulative review, seasonal practice, centers, early finisher work, and more.

I use both concept-based math projects to focus on specific standards and seasonal math projects that integrate several skills.

Error Analysis
Finally, error analysis is always a challenging way to encourage critical thinking. When we use error analysis, we encourage students to analyze their own mistakes to prevent making the same mistakes in the future.
For my gifted students, I use error analysis tasks as an assessment when they have shown mastery of a unit during other tasks. For students in the regular classroom needing enrichment, I usually have them complete the tasks in a center or with a partner.
For students needing extra support, we complete error analysis in small groups. We go step-by-step through the concept and they are always able to eventually identify what the error is. It is so empowering to students when they finally figure out the error AND it helps prevent them from making the same error in the future!
My FREE addition error analysis is a good place to start, no matter the grade level. I show them the process of walking through the problem and how best to complete an error analysis task.
When you’re ready for more, this bundle of error analysis tasks contains more than 240 tasks to engage and enrich your students in critical thinking practice.

If you want to dig even deeper, visit this conceptual vs computational error analysis post to learn more about using error analysis in the classroom.

Related Critical Thinking Posts
- How to Increase Critical Thinking and Creativity in Your “Spare” Time
- More Tips to Increase Critical Thinking
Critical thinking is essential for students to develop a deeper understanding of math concepts, problem-solving skills, and a stronger ability to reason logically. When you learn how to encourage critical thinking in math, you’re setting your students up for success not only in more advanced math subjects they’ll encounter, but also in life.
How do you integrate critical thinking in your classroom? Come share your ideas with us in our FREE Inspired In Upper Elementary Facebook group .

Mary Montero
I’m so glad you are here. I’m a current gifted and talented teacher in a small town in Colorado, and I’ve been in education since 2009. My passion (other than my family and cookies) is for making teachers’ lives easier and classrooms more engaging.
You might also like…

Leave a Reply Cancel reply
Your email address will not be published. Required fields are marked *
One Comment
Mary Thankyou for your inspirational activities. I have just read and loved the morning talk activities. I do have meetings with my students but usually at end of day. What time do you

©2023 Teaching With a Mountain View . All Rights Reserved | Designed by Ashley Hughes
Username or Email Address
Remember Me
Lost your password?
Review Cart
No products in the cart.

Applying Algebraic Strategies to Make Gains in How You Think
Using mathematical inversion to improve critical thinking..
Posted August 31, 2023 | Reviewed by Lybi Ma
- Purposely playing devil's advocate can improve your critical thinking.
- Adopting the rule of five approach to lateral thinking provides good critical thinking practise.
- We need to overcome our own psychological predispositions to become good critical thinkers.
When it comes to critical thinking, we are at the mercy of our brain’s own psychological predispositions, which make us naturally poor at thinking impartially. Confirmation bias encourages us to favour patterns and discount new information; truth bias makes us assume everything is true; and the illusory truth effect makes us poor at indexing information, meaning we’ll start to believe something is true, even if we know that it is false.
What’s more, the more times we encounter information, the more we believe it, and even when we practice being sceptical, our brains assume the worst and make us overcompensate in our fact-checking, making it hard to identify what is and isn’t real. Add to these predispositions the influence of the opinions and values we already hold, and we’re a melting pot of ideas that totally prevent impartiality. We’re also susceptible to outside influence, and naturally seek out individuals or groups with ideas that complement our own; the beginnings of groupthink .
When it seems that even our brains are against us, our potential saviour comes in the form of critical thinking. Specifically focussed on improving our ability to think impartially, rationally, and analytically, and to slow down our thought processing to become more effective, critical thinking has a direct impact on our mental capability, particularly when it comes to external influence. It is, and should be, the first line of defence in identifying fake news and propaganda, helping prevent the development of extremist views, and ultimately fostering an improved understanding of the information we consume. It also helps reduce our susceptibility to coercion and manipulation.
A novel approach to critical thinking is to emulate the mathematical approach to equations, which utilise inversion to problem-solve. For mathematicians, it is second nature to invert an equation to make it easier to solve, aligning all information of one type, on one side of the equation. It’s what helps to calculate “x” and is a method of showing your working, which encourages slower more deliberate thinking.
While that makes sense for calculating x/y, the question is how can it apply to much more complex subjects? Subjects that are anything but linear, infinitely complex, and which can have any number of attributes and conflicting facts . Well, it’s not so much the pure mathematical approach that we need to apply, but the principle of what it is and what it represents.
Inversion thinking can be applied to any amount of information, and the purpose is to encourage us to deliberately approach information in a contrary way. By specifically imagining an alternative scenario, playing devil’s advocate, seeking out conflicting or alternative sources and viewpoints, and actively challenging our own, it makes us far better able to determine fact from fiction and recognise our own bias in how we process and rationalise information. Our goal with this form of critical thinking is not necessarily to reach an answer, but to be sure that we have considered something from multiple angles, and challenged our own perceptions about what is fact and what is fiction. The result should be better quality decision-making and more informed understanding, but this should not be the primary goal when practising critical thinking.
We encourage the rule of five as an approach to lateral reading, the perfect instigator of the inversion approach. Lateral reading encourages the breadth rather than depth of reading, promoting that you seek multiple resources, and filter common facts from opinions across multiple resources. In turn, the rule of five helps practise lateral thinking, by actively tasking you with finding:
- Two sources of information that you are comfortable or familiar with, preferably across two different mediums, for example, article and video
- Two sources of information that you are definitely not comfortable or familiar with, preferably ones that directly contradict or challenge your own viewpoints
- A source of information that has a very specific, niche, or strong opinion on the matter
The purpose of seeking out multiple sources of information is that it allows you to identify commonalities (points that persist in all formats); challenge your own bias by directly contradicting them; and help you to identify flaws in your own arguments or reasoning. It encourages you to actively practise critical thinking, in turn making you better at it, and it makes you less susceptible to exploitation, manipulation, and misinformation, all of which are rife in a society where we consume so much content.
Mathematical Teaching Strategies: Pathways to Critical Thinking and Metacognition. International Journal of Research in Education and Science.

The Open Minds Foundation is dedicated to undermining the effects of coercive control, through critical thinking education and training.
- Find a Therapist
- Find a Treatment Center
- Find a Psychiatrist
- Find a Support Group
- Find Online Therapy
- United States
- Brooklyn, NY
- Chicago, IL
- Houston, TX
- Los Angeles, CA
- New York, NY
- Portland, OR
- San Diego, CA
- San Francisco, CA
- Seattle, WA
- Washington, DC
- Asperger's
- Bipolar Disorder
- Chronic Pain
- Eating Disorders
- Passive Aggression
- Personality
- Goal Setting
- Positive Psychology
- Stopping Smoking
- Low Sexual Desire
- Relationships
- Child Development
- Self Tests NEW
- Therapy Center
- Diagnosis Dictionary
- Types of Therapy

At any moment, someone’s aggravating behavior or our own bad luck can set us off on an emotional spiral that threatens to derail our entire day. Here’s how we can face our triggers with less reactivity so that we can get on with our lives.
- Emotional Intelligence
- Gaslighting
- Affective Forecasting
- Neuroscience
An official website of the United States government
The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.
The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.
- Publications
- Account settings
Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .
- Advanced Search
- Journal List

Does mathematics training lead to better logical thinking and reasoning? A cross-sectional assessment from students to professors
Clio cresswell.
1 School of Mathematics and Statistics, The University of Sydney, Sydney, Australia
Craig P. Speelman
2 School of Arts and Humanities, Edith Cowan University, Joondalup, Australia
Associated Data
All relevant data are within the paper and its Supporting Information files.
Mathematics is often promoted as endowing those who study it with transferable skills such as an ability to think logically and critically or to have improved investigative skills, resourcefulness and creativity in problem solving. However, there is scant evidence to back up such claims. This project tested participants with increasing levels of mathematics training on 11 well-studied rational and logical reasoning tasks aggregated from various psychological studies. These tasks, that included the Cognitive Reflection Test and the Wason Selection Task, are of particular interest as they have typically and reliably eluded participants in all studies, and results have been uncorrelated with general intelligence, education levels and other demographic information. The results in this study revealed that in general the greater the mathematics training of the participant, the more tasks were completed correctly, and that performance on some tasks was also associated with performance on others not traditionally associated. A ceiling effect also emerged. The work is deconstructed from the viewpoint of adding to the platform from which to approach the greater, and more scientifically elusive, question: are any skills associated with mathematics training innate or do they arise from skills transfer?
Introduction
Mathematics is often promoted as endowing those who study it with a number of broad thinking skills such as: an ability to think logically, analytically, critically and abstractly; having capacity to weigh evidence with impartiality. This is a view of mathematics as providing transferable skills which can be found across educational institutions, governments and corporations worldwide. A view material to the place of mathematics in curricula.
Consider the UK government’s commissioned inquiry into mathematics education “Making Mathematics Count” ascertaining the justification that “mathematical training disciplines the mind, develops logical and critical reasoning, and develops analytical and problem-solving skills to a high degree” [ 1 p11]. The Australian Mathematical Sciences Institute very broadly states in its policy document “Vision for a Maths Nation” that “Not only is mathematics the enabling discipline, it has a vital productive role planning and protecting our well-being” (emphasis in original) [ 2 ]. In Canada, British Columbia’s New 2016 curriculum K-9 expressly mentions as part of its “Goals and Rationale”: “The Mathematics program of study is designed to develop deep mathematical understanding and fluency, logical reasoning, analytical thought, and creative thinking.” [ 3 ]. Universities, too, often make such specific claims with respect to their teaching programs. “Mathematics and statistics will help you to think logically and clearly, and apply a range of problem-solving strategies” is claimed by The School of Mathematical Sciences at Monash University, Australia [ 4 ]. The School of Mathematics and Statistics at The University of Sydney, Australia, directly attributes as part of particular course objectives and outcomes skills that include “enhance your problem-solving skills” as part of studies in first year [ 5 ], “develop logical thinking” as part of studies in second year, which was a statement drafted by the lead author in fact [ 6 ], and “be fluent in analysing and constructing logical arguments” as part of studies in third year [ 7 ]. The University of Cambridge’s Faculty of Mathematics, UK, provides a dedicated document “Transferable Skills in the Mathematical Tripos” as part of its undergraduate mathematics course information, which again lists “analytic ability; creativity; initiative; logical and methodical reasoning; persistence” [ 8 ].
In contrast, psychological research, which has been empirically investigating the concept of transferability of skills since the early 1900s, points quite oppositely to reasoning skills as being highly domain specific [ 9 ]. Therefore, support for claims that studying mathematics engenders more than specific mathematics knowledge is highly pertinent. And yet it is largely absent. The 2014 Centre for Curriculum Redesign (CCR) four part paper “Mathematics for the 21st Century: What Should Students Learn?” concludes in its fourth paper titled “Does mathematics education enhance higher-order thinking skills?” with a call to action “… there is not sufficient evidence to conclude that mathematics enhances higher order cognitive functions. The CCR calls for a much stronger cognitive psychology and neuroscience research base to be developed on the effects of studying mathematics” [ 10 ].
Inglis and Simpson [ 11 ], bringing up this very issue, examined the ability of first-year undergraduate students from a high-ranking UK university mathematics department, on the “Four Cards Problem” thinking task, also known as the Wason Selection Task. It is stated as follows.
Each of the following cards have a letter on one side and a number on the other.

Here is a rule: “if a card has a D on one side, then it has a 3 on the other”. Your task is to select all those cards, but only those cards, which you would have to turn over in order to find out whether the rule is true or false. Which cards would you select?
This task involves understanding conditional inference, namely understanding the rule “If P then Q” and with this, deducing the answer as “P and not Q” or “D and 7”. Such logical deduction indeed presents as a good candidate to test for a potential ability of the mathematically trained. This task has also been substantially investigated in the domain of the psychology of reasoning [ 12 p8] revealing across a wide range of publications that only around 10% of the general population reach the correct result. The predominant mistake being to pick “D and 3”; where in the original study by Wason [ 13 ] it is suggested that this was picked by 65% of people. This poor success rate along with a standard mistake has fuelled interest in the task as well as attempts to understand why it occurs. A prevailing theory being the so named matching bias effect; the effect of disproportionately concentrating on items specifically mentioned in the situation, as opposed to reasoning according to logical rules.
Inglis and Simpson’s results isolated mathematically trained individuals with respect to this task. The participants were under time constraint and 13% of the first-year undergraduate mathematics students sampled reached the correct response, compared to 4% of the non-mathematics (arts) students that was included. Of note also was the 24% of mathematics students as opposed to 45% of the non-mathematics students who chose the standard mistake. The study indeed unveiled that mathematically trained individuals were significantly less affected by the matching bias effect with this problem than the individuals without mathematics training. However, the achievement of the mathematically trained group was still far from masterful and the preponderance for a non-standard mistake compared with non-mathematically trained people is suggestive. Mathematical training appears to engender a different thinking style, but it remains unclear what the difference is.
Inglis, Simpson and colleagues proceeded to follow up their results with a number of studies concentrated on conditional inference in general [ 14 , 15 ]. A justification for this single investigatory pathway being that if transfer of knowledge is present, something subtle to test for in the first place, a key consideration should be the generalisation of learning rather than the application of skills learned in one context to another (where experimenter bias in the choice of contexts is more likely to be an issue). For this they typically used sixteen “if P then Q” comprehension tasks, where their samples across a number of studies have included 16-year-old pre-university mathematics students (from England and Cyprus), mathematics honours students in their first year of undergraduate university study, third year university mathematics students, and associated control groups. The studies have encompassed controls for general intelligence and thinking disposition prior to training, as well as follows ups of up to two years to address the issue of causation. The conclusive thinking pattern that has emerged is a tendency of the mathematical groups towards a greater likelihood of rejecting the invalid denial of the antecedent and affirmation of the consequent inferences. But with this, and this was validated by a second separate study, the English mathematics group actually became less likely to endorse the valid modus tollens inference. So again, mathematical training appears to engender a different thinking style, but there are subtleties and it remains unclear what the exact difference is.
This project was designed to broaden the search on the notion that mathematics training leads to increased reasoning skills. We focused on a range of reasoning problems considered in psychological research to be particularly insightful into decision making, critical thinking and logical deduction, with their distinction in that the general population generally struggles with answering them correctly. An Australian sample adds diversity to the current enquiries that have been European focussed. Furthermore, in an effort to identify the impact of mathematics training through a possible gradation effect, different levels of mathematically trained individuals were tested for performance.
Well-studied thinking tasks from a variety of psychological studies were chosen. Their descriptions, associated success rates and other pertinent details follows. They were all chosen as the correct answer is typically eluded for a standard mistake.
The three-item Cognitive Reflection Test (CRT) was used as introduced by Frederick [ 16 ]. This test was devised in line with the theory that there are two general types of cognitive activity: one that operates quickly and without reflection, and another that requires not only conscious thought and effort, but also an ability to reflect on one’s own cognition by including a step of suppression of the first to reach it. The three items in the test involve an incorrect “gut” response and further cognitive skill is deemed required to reach the correct answer (although see [ 17 ] for evidence that correct responses can result from “intuition”, which could be related to intelligence [ 18 ]).
In a lake, there is a patch of lily pads. Every day, the patch doubles in size. If it takes 48 days for the patch to cover the entire lake, how long would it take for the patch to cover half of the lake?
If it takes 5 machines 5 minutes to make 5 widgets, how long would it take 100 machines to make 100 widgets?
Bat and ball
A bat and a ball cost $1.10 in total. The bat costs a dollar more than the ball. How much does the ball cost?
The solutions are: 47 days for the Lily Pads problem, 5 minutes for the Widgets problem and 5 cents for the Bat and Ball problem. The considered intuitive, but wrong, answers are 24 days, 100 minutes and 10 cents, respectively. These wrong answers are attributed to participants becoming over focused on the numbers so as to ignore the exponential growth pattern in the Lily Pads problem, merely complete a pattern in numbers in the Widgets problem, and neglect the relationship “more than” in the Bat and Ball problem [ 19 ]. The original study by Frederick [ 16 ] provides a composite measure of the performance on these three items, with only 17% of those studied (n = 3428) reaching the perfect score. The CRT has since been studied extensively [ 19 – 21 ]. Research using the CRT tends not to report performance on the individual items of the test, but rather a composite measure of performance. Attridge and Inglis [ 22 ] used the CRT as a test for thinking disposition of mathematics students as one way to attempt to disentangle the issue of filtering according to prior thinking styles rather than transference of knowledge in successful problem solving. They repeat tested 16-year old pre-university mathematics students and English literature students without mathematics subjects at a one-year interval and found no difference between groups.
Three problems were included that test the ability to reason about probability. All three problems were originally discussed by Kahneman and Tversky [ 23 ], with the typically poor performance on these problems explained by participants relying not on probability knowledge, but a short-cut method of thinking known as the representativeness heuristic. In the late 1980s, Richard Nisbett and colleagues showed that graduate level training in statistics, while not revealing any improvement in logical reasoning, did correlate with higher-quality statistical answers [ 24 ]. Their studies lead in particular to the conclusion that comprehension of, what is known as the law of large numbers, did show improvement with training. The first of our next three problems targeted this law directly.
A certain town is served by two hospitals. In the larger hospital, about 45 babies are born each day, and in the smaller hospital, about 15 babies are born each day. As you know, about 50 percent of all babies are boys. However, the exact percentage varies from day to day. Sometimes it may be higher than 50 percent, sometimes lower. For a period of one year, each hospital recorded the number of days on which more than 60 percent of the babies born were boys. Which hospital do you think recorded more such days? (Circle one letter.)
- (a) the larger hospital
- (b) the smaller hospital
- (c) about the same (that is, within 5 percent of each other)
Kahneman and Tversky [ 23 ] reported that, of 50 participants, 12 chose (a), 10 chose (b), and 28 chose (c). The correct answer is (b), for the reason that small samples are more likely to exhibit extreme events than large samples from the same population. The larger the sample, the more likely it will exhibit characteristics of the parent population, such as the proportion of boys to girls. However, people tend to discount or be unaware of this feature of sampling statistics, which Kahneman and Tversky refer to as the law of large numbers. Instead, according to Kahneman and Tversky, people tend to adhere to a fallacious law of small numbers, where even small samples are expected to exhibit properties of the parent population, as illustrated by the proportion of participants choosing the answer (c) in their 1972 study. Such thinking reflects use of the representativeness heuristic, whereby someone will judge the likelihood of an uncertain event based on how similar it is to characteristics of the parent population of events.
Birth order
All families of six children in a city were surveyed. In 72 families the exact order of births of boys and girls was GBGBBG.
- (a) What is your estimate of the number of families surveyed in which the exact order of births was BGBBBB?
- (b) In the same survey set, which, if any, of the following two sequences would be more likely: BBBGGG or GBBGBG?
All of the events listed in the problem have an equal probability, so the correct answer to (a) is 72, and to (b) is “neither is more likely”. Kahneman and Tversky [ 23 ] reported that 75 of 92 participants judged the sequence in (a) as less likely than the given sequence. A similar number (unspecified by Kahneman and Tversky, but the statistical effect was reported to be of the same order as in (a)) reported that GBBGBG was the more likely sequence. Again, Kahneman and Tversky suggested that these results reflected use of the representativeness heuristic. In the context of this problem, the heuristic would have taken the following form: some birth orders appear less patterned than others, and less patterned is to be associated with the randomness of birth order, making them more likely.
Coin tosses
In a sequence of coin tosses (the coin is fair) which of the following outcomes would be most likely (circle one letter):
- (a) H T H T H T H T
- (b) H H H H T T T T
- (c) T T H H T T H H
- (d) H T T H T H H T
- (e) all of the above are equally likely
The correct answer in this problem is (e). Kahneman and Tversky [ 23 ] reported that participants tend to choose less patterned looking sequences (e.g., H T T H T H H T) as more likely than more systematic looking sequences (e.g., H T H T H T H T). This reasoning again reflects the representativeness heuristic.
Three further questions from the literature were included to test problem solving skill.
Two drivers
Two drivers set out on a 100-mile race that is marked off into two 50-mile sections. Driver A travels at exactly 50 miles per hour during the entire race. Driver B travels at exactly 45 mph during the first half of the race (up to the 50-mile marker) and travels at exactly 55 mph during the last half of the race (up to the finish line). Which of the two drivers would win the race? (Circle one letter.)
- (a) Driver A would win the race
- (b) Driver B would win the race
- (c) the two drivers would arrive at the same time (within a few seconds of one another)
This problem was developed by Pelham and Neter [ 25 ]. The correct answer is (a), which can be determined by calculations of driving times for each Driver, using time = distance/velocity. Pelham and Neter argue, however, that (c) is intuitively appealing, on the basis that both drivers appear to have the same overall average speed. Pelham and Neter reported that 67% of their sample gave this incorrect response to the problem, and a further 13% selected (b).
Petrol station
Imagine that you are driving along the road and you notice that your car is running low on petrol. You see two petrol stations next to each other, both advertising their petrol prices. Station A’s price is 65c/litre; Station B’s price is 60c/litre. Station A’s sign also announces: “5c/litre discount for cash!” Station B’s sign announces “5c/litre surcharge for credit cards.” All other factors being equal (for example, cleanliness of the stations, number of cars waiting at each etc), to which station would you choose to go, and why?
This problem was adapted from one described by Galotti [ 26 ], and is inspired by research reported by Thaler [ 27 ]. According to Thaler’s research, most people prefer Station A, even though both stations are offering the same deal: 60c/litre for cash, and 65c/litre for credit. Tversky and Kahneman [ 28 ] explain this preference by invoking the concept of framing effects. In the context of this problem, such an effect would involve viewing the outcomes as changes from some initial point. The initial point frames the problem, and provides a context for viewing the outcome. Thus, depending on the starting point, outcomes in this problem can be viewed as either a gain (in Station A, you gain a discount if you use cash) or a loss (in Station B, you are charged more (a loss) for using credit). Given that people are apparently more concerned about a loss than a gain [ 29 ], the loss associated with Station B makes it the less attractive option, and hence the preference for Station A. The correct answer, though, is that the stations are offering the same deal and so no station should be preferred.
And finally, a question described by Stanovich [ 30 , 31 ] as testing our predisposition for cognitive operations that require the least computational effort.
Jack looking at Anne
Jack is looking at Anne, but Anne is looking at George. Jack is married, but George is not. Is a married person looking at an unmarried person? (Circle one letter.)
- (c) Cannot be determined
Stanovich reported that over 80% of people choose the “lazy” answer (c). The correct answer is (a).
The above questions survey, in a clear problem solving setting, an ability to engage advanced cognitive processing in order to critically evaluate and possibly override initial gut reasoning, an ability to reason about probability within the framework of the law of large numbers and the relationship between randomness and patterning, an ability to isolate salient features of a problem and, with the last question in particular, an ability to map logical relations. It might be hypothesised that according to degrees of mathematical training, in line with the knowledge base provided and the claims of associated broad and enhanced problem-solving abilities in general, that participants with greater degrees of such training would outperform others on these questions. This hypothesis was investigated in this study. In addition, given that no previous study on this issue has examined the variety of problems used in this study, we also undertook an exploratory analysis to investigate whether there exist any associations between the problems in terms of their likelihood of correct solution. Similarities between problems might indicate which problem solving domains could be susceptible to the effects of mathematics training.
A questionnaire was constructed containing the problems described in the previous sections plus the Four Cards Problem as tested by Inglis and Simpson [ 11 ] for comparison. The order of the problems was as follows: 1) Lily Pads; 2) Hospitals; 3) Widgets; 4) Four Cards; 5) Bat and Ball; 6) Birth Order; 7) Petrol Station; 8) Coin Tosses; 9) Two Drivers; 10) Jack looking at Anne. It was administered to five groups distinctive in mathematics training levels chosen from a high-ranking Australian university, where the teaching year is separated into two teaching semesters and where being a successful university applicant requires having been highly ranked against peers in terms of intellectual achievement:
- Introductory—First year, second semester, university students with weak high school mathematical results, only enrolled in the current unit as a compulsory component for their chosen degree, a unit not enabling any future mathematical pathway, a typical student may be enrolled in a Biology or Geography major;
- Standard—First year, second semester, university students with fair to good high school mathematical results, enrolled in the current mathematics unit as a compulsory component for their chosen degree with the possibility of including some further mathematical units in their degree pathway, a typical student may be enrolled in an IT or Computer Science major;
- Advanced1—First year, second semester, university mathematics students with very strong interest as well as background in mathematics, all higher year mathematical units are included as possible future pathway, a typical student may be enrolled in a Mathematics or Physics major;
- Advanced2—Second year, second semester, university mathematics students with strong interest as well as background in mathematics, typically a direct follow on from the previously mentioned Advanced1 cohort;
- Academic—Research academics in the mathematical sciences.
Participants
123 first year university students volunteered during “help on demand” tutorial times containing up to 30 students. These are course allocated times that are supervised yet self-directed by students. This minimised disruption and discouraged coercion. 44 second year university students completed the questionnaire during a weekly one-hour time slot dedicated to putting the latest mathematical concepts to practice with the lecturer (whereby contrast to what occurs in tutorial times the lecturer does most of the work and all students enrolled are invited). All these university students completed the questionnaire in normal classroom conditions; they were not placed under strict examination conditions. The lead author walked around to prevent discussion and coercion and there was minimum disruption. 30 research academics responded to local advertising and answered the questionnaire in their workplace while supervised.
The questionnaires were voluntary, anonymous and confidential. Participants were free to withdraw from the study at any time and without any penalty. No participant took this option however. The questionnaires gathered demographic information which included age, level of education attained and current qualification pursued, name of last qualification and years since obtaining it, and an option to note current speciality for research academics. Each problem task was placed on a separate page. Participants were not placed under time constraint, but while supervised, were asked to write their start and finish times on the front page of the survey to note approximate completion times. Speed of completion was not incentivised. Participants were not allowed to use calculators. A final “Comments Page” gave the option for feedback including specifically if the participants had previously seen any of the questions. Questionnaires were administered in person and supervised to avoid collusion or consulting of external sources.
The responses were coded four ways: A) correct; B) standard error (the errors discussed above in The Study); C) other error; D) left blank.
The ethical aspects of the study were approved by the Human Research Ethics Committee of the University of Sydney, protocol number [2016/647].
The first analysis examined the total number of correct responses provided by the participants as a function of group. Scores ranged from 1 to 11 out of a total possible of 11 (Problem 6 had 2 parts) ( Fig 1 ). An ANOVA of this data indicated a significant effect of group (F(4, 192) = 20.426, p < .001, partial η 2 = .299). Pairwise comparisons using Tukey’s HSD test indicated that the Introductory group performed significantly worse than the Advanced1, Advanced2 and Academic groups. There were no significant differences between the Advanced1, Advanced2 and Academic groups.

Error bars are one standard error of the mean.
Overall solution time, while recorded manually and approximately, was positively correlated with group, such that the more training someone had received, the longer were these solution times (r(180) = 0.247, p = .001). However, as can be seen in Fig 2 , this relationship is not strong.

A series of chi-squared analyses, and their Bayesian equivalents, were performed on each problem, to determine whether the distribution of response types differed as a function of group. To minimise the number of cells in which expected values in some of these analyses were less than 5, the Standard Error, Other Error and Blank response categories were collapsed into one category (Incorrect Response). For three of the questions, the expected values of some cells did fall below 5, and this was due to most people getting the problem wrong (Four Cards), or most people correctly responding to the problem (Bat and Ball, Coin Tosses). In these cases, the pattern of results was so clear that a statistical analysis was barely required. Significant chi-squared results were examined further with pairwise posthoc comparisons (see Table 1 ).
| Introductory | Standard | Advanced1 | Advanced2 | Academic | |
|---|---|---|---|---|---|
| n | 62 | 27 | 34 | 44 | 30 |
| Mean Age (yrs) | 19.3 | 18.9 | 18.6 | 20.0 | 40.2 |
| Response Type | |||||
| d,e | d,e | a,b | a,b | ||
| Correct | 5% | 4% | 12% | 39% | 37% |
| Standard Error | 47% | 41% | 21% | 18% | 7% |
| Other Error | 45% | 52% | 65% | 43% | 57% |
| Blank | 3% | 4% | 3% | 0% | 0% |
| c,d | a | a | |||
| Correct | 55% | 78% | 85% | 82% | 100% |
| Standard Error | 29% | 11% | 3% | 9% | 0% |
| Other Error | 15% | 7% | 12% | 9% | 0% |
| Blank | 2% | 4% | 0% | 0% | 0% |
| c,d,e | a | a | a | ||
| Correct | 48% | 74% | 82% | 82% | 87% |
| Standard Error | 31% | 11% | 15% | 11% | 7% |
| Other Error | 18% | 15% | 3% | 7% | 7% |
| Blank | 3% | 0% | 0% | 0% | 0% |
| Correct | 60% | 89% | 100% | 93% | 90% |
| Standard Error | 31% | 11% | 0% | 5% | 7% |
| Other Error | 8% | 0% | 0% | 2% | 0% |
| Blank | 2% | 0% | 0% | 0% | 3% |
| Correct | 32% | 48% | 44% | 52% | 47% |
| Standard Error | 48% | 44% | 53% | 43% | 50% |
| Other Error | 18% | 7% | 3% | 5% | 3% |
| Blank | 2% | 0% | 0% | 0% | 0% |
| c,d,e | a | a | a | ||
| Correct | 35% | 52% | 71% | 66% | 83% |
| Standard Error | 35% | 22% | 18% | 9% | 13% |
| Other Error | 16% | 15% | 9% | 16% | 3% |
| Blank | 13% | 11% | 3% | 9% | 0% |
| d | a | ||||
| Correct | 53% | 63% | 88% | 82% | 93% |
| Standard Error | 34% | 19% | 9% | 14% | 3% |
| Other Error | 3% | 7% | 0% | 2% | 3% |
| Blank | 10% | 11% | 3% | 2% | 0% |
| Correct | 92% | 96% | 91% | 84% | 93% |
| Standard Error | 3% | 4% | 3% | 5% | 0% |
| Other Error | 3% | 0% | 6% | 11% | 7% |
| Blank | 2% | 0% | 0% | 0% | 0% |
| c,d,e | c,d,e | a,b | a,b | a,b | |
| Correct | 16% | 19% | 56% | 64% | 73% |
| Standard Error | 71% | 67% | 29% | 25% | 23% |
| Other Error | 11% | 15% | 15% | 11% | 3% |
| Blank | 2% | 0% | 0% | 0% | 0% |
| Correct | 50% | 56% | 59% | 55% | 73% |
| Standard Error | 27% | 22% | 18% | 25% | 3% |
| Other Error | 21% | 22% | 24% | 20% | 20% |
| Blank | 2% | 0% | 0% | 0% | 3% |
| d,e | a | a | |||
| Correct | 19% | 19% | 29% | 48% | 53% |
| Standard Error | 71% | 81% | 68% | 52% | 47% |
| Other Error | 6% | 0% | 3% | 0% | 0% |
| Blank | 3% | 0% | 0% | 0% | 0% |
Superscripts label the groups (e.g., Introductory = a). Within the table, these letters refer to which other group a particular group was significantly different to according to a series of pairwise post hoc chi squared analyses (Bonferroni corrected α = .005) (e.g., ‘d’ in the Introductory column indicates the Introductory and the Advanced2 (d) group were significantly different for a particular problem).
The three groups with the least amount of training in mathematics were far less likely than the other groups to give the correct solution (χ 2 (4) = 31.06, p < .001; BF 10 = 45,045) ( Table 1 ). People in the two most advanced groups (Advanced2 and Academic) were more likely to solve the card problem correctly, although it was still less than half of the people in these groups who did so. Further, these people were less likely to give the standard incorrect solution, so that most who were incorrect suggested some more cognitively elaborate answer, such as turning over all cards. The proportion of people in the Advanced2 and Academic groups (39 and 37%) who solved the problem correctly far exceeded the typical proportion observed with this problem (10%). Of note, also, is the relatively high proportion of those in the higher training groups who, when they made an error, did not make the standard error, a similar result to the one reported by Inglis and Simpson [ 11 ].
The cognitive reflection test
In the Lily Pads problem, although most people in the Standard, Advanced1, Advanced2 and Academic groups were likely to select the correct solution, it was also the case that the less training someone had received in mathematics, the more likely they were to select an incorrect solution (χ 2 (4) = 27.28, p < .001; BF 10 = 15,554), with the standard incorrect answer being the next most prevalent response for the two lower ability mathematics groups ( Table 1 ).
Performance on the Widgets problem was similar to performance on the Lily Pads problem in that most people in the Standard, Advanced1, Advanced2 and Academic groups were likely to select the correct solution, but that the less training someone had received in mathematics, the more likely they were to select an incorrect solution (χ 2 (4) = 23.76, p< .001; BF 10 = 516) ( Table 1 ). As with the Lily Pads and Widget problems, people in the Standard, Advanced1, Advanced2 and Academic groups were highly likely to solve the Bat and Ball problem (χ 2 (4) = 35.37, p < .001; BF 10 = 208,667). Errors were more likely from the least mathematically trained people (Introductory, Standard) than the other groups ( Table 1 ).
To compare performance on the CRT with previously published results, performance on the three problems (Lily Pads, Widgets, Bat and Ball) were combined. The number of people in each condition that solved 0, 1, 2, or 3 problems correctly is presented in Table 2 . The Introductory group were evenly distributed amongst the four categories, with 26% solving all three problems correctly. Around 70% of the rest of the groups solved all 3 problems correctly, which is vastly superior to the 17% reported by Frederick [ 16 ].
| Introductory | Standard | Advanced1 | Advanced2 | Academic | |
|---|---|---|---|---|---|
| N | 62 | 27 | 34 | 44 | 30 |
| Number correct | |||||
| 0 | 21% | 0% | 0% | 0% | 0% |
| 1 | 21% | 30% | 3% | 14% | 0% |
| 2 | 32% | 0% | 26% | 16% | 23% |
| 3 | 26% | 70% | 71% | 70% | 77% |
Responses to the Hospitals problem were almost universally split between correct and standard errors in the Standard, Advanced1, Advanced2 and Academic groups. Although this pattern of responses was also evident in the Introductory group, this group also exhibited more non-standard errors and non-responses than the other groups. However, the differences between the groups were not significant (χ 2 (4) = 4.93, p = .295; BF 10 = .068) ( Table 1 ). Nonetheless, the performance of all groups exceeds the 20% correct response rate reported by Kahneman and Tversky [ 23 ].
The two versions of the Birth Order problem showed similar results, with correct responses being more likely in the groups with more training (i.e., Advanced1, Advanced2 and Academic), and responses being shared amongst the various categories in the Introductory and Standard groups (χ a 2 (4) = 24.54, p < .001; BF 10 = 1,303; χ b 2 (4) = 25.77, p < .001; BF 10 = 2,970) ( Table 1 ). Nonetheless, performance on both versions of the problem in this study was significantly better than the 82% error rate reported by Kahneman and Tversky [ 23 ].
The Coin Tosses problem was performed well by all groups, with very few people in any condition committing errors. There were no obvious differences between the groups (χ 2 (4) = 3.70, p = .448; BF 10 = .160) ( Table 1 ). Kahneman and Tversky [ 23 ] reported that people tend to make errors on this type of problem by choosing less patterned looking sequences, but they did not report relative proportions of people making errors versus giving correct responses. Clearly the sample in this study did not perform like those in Kahneman and Tversky’s study.
Responses on the Two Drivers problem were clearly distinguished by a high chance of error in the Introductory and Standard groups (over 80%), and a fairly good chance of being correct in the Advanced1, Advanced2 and Academic groups (χ 2 (4) = 46.16, p < .001; BF 10 = 1.32 x 10 8 ) ( Table 1 ). Academics were the standout performers on this problem, although over a quarter of this group produced an incorrect response. Thus, the first two groups performed similarly to the participants in the Pelham and Neter [ 25 ] study, 80% of whom gave an incorrect response.
Responses on the Petrol Station problem were marked by good performance by the Academic group (73% providing a correct response), and just over half of each of the other groups correctly solving the problem. This difference was not significant (χ 2 (4) = 4.68, p = .322: BF 10 = .059) ( Table 1 ). Errors were fairly evenly balanced between standard and other, except for the Academic group, who were more likely to provide a creative answer if they made an error. Thaler [ 27 ] reported that most people get this problem wrong. In this study, however, on average, most people got this problem correct, although this average was boosted by the Academic group.
Responses on the Jack looking at Anne problem generally were standard errors, except for the Advanced2 and Academic groups, which were evenly split between standard errors and correct responses (χ 2 (4) = 18.03, p = .001; BF 10 = 46) ( Table 1 ). Thus, apart from these two groups, the error rate in this study was similar to that reported by Stanovich [ 30 ], where 80% of participants were incorrect.
A series of logistic regression analyses were performed in order to examine whether the likelihood of solving a particular problem correctly could be predicted on the basis of whether other problems were solved correctly. Each analysis involved selecting performance (correct or error) on one problem as the outcome variable, and performance on the other problems as predictor variables. Training (amount of training) was also included as a predictor variable in each analysis. A further logistic regression was performed with training as the outcome variable, and performance on all of the problems as predictor variables. The results of these analyses are summarised in Table 3 . There were three multi-variable relationships observed in these analyses, which can be interpreted as the likelihood of solving one problem in each group being associated with solving the others in the set. These sets were: (1) Lily Pads, Widgets and Petrol Station; (2) Hospitals, Four Cards and Two Drivers; (3) Birth Order and Coin Tosses. Training also featured in each of these sets, moderating the relationships as per the results presented above for each problem.
| Predictor Variables | ||||||||||||||
| P1 | P2 | P3 | P4 | P5 | P6a | P6b | P7 | P8 | P9 | P10 | Training | P | % | |
| Outcome Variables | ||||||||||||||
| P1 | - | ✓ | ✓ | ✓ | < .001 | 83.8 | ||||||||
| P2 | - | ✓ | .030 | 64.5 | ||||||||||
| P3 | ✓ | - | ✓ | < .001 | 80.2 | |||||||||
| P4 | ✓ | - | ✓ | ✓ | < .001 | 85.3 | ||||||||
| P5 | - | ✓ | < .001 | 83.8 | ||||||||||
| P6a | - | ✓ | < .001 | 78.2 | ||||||||||
| P6b | ✓ | - | ✓ | ✓ | < .001 | 79.2 | ||||||||
| P7 | ✓ | - | < .001 | 74.1 | ||||||||||
| P8 | ✓ | - | ✓ | .003 | 91.4 | |||||||||
| P9 | ✓ | - | ✓ | < .001 | 75.6 | |||||||||
| P10 | - | .001 | 74.1 | |||||||||||
| training | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | - | < .001 | - | |||||
P = Problem (1 = Four Cards; 2 = Lily Pads; 3 = Widgets; 4 = Bat & Ball; 5 = Hospitals; 6a = Birth Order (a); 6b = Birth Order (b); 7 = Coin Tosses; 8 = Two Drivers; 9 = Petrol Station; 10 = Jack looking at Anne).
training = Amount of training condition.
p = significance level of logistic regression model.
% = percentage of cases correctly classified by the logistic regression model.
✓ = significant predictor, α < .05.
* = logistic regression for the training outcome variable is multinomial, whereas all other logistic regressions are binomial.
The final “Comments Page” revealed the participants as overwhelmingly enjoying the questions. Any analysis of previous exposure to the tasks proved impossible as there was little to no alignment on participant’s degree of recall, if any, and even perceptions of what exposure entailed. For example, some participants confused being exposed to the particular tasks with being habitually exposed to puzzles, or even mathematics problems, more broadly.
In general, the amount of mathematics training a group had received predicted their performance on the overall set of problems. The greater the training, the more problems were answered correctly, and the slower the recorded response times. There was not an obvious difference between the Advanced1, Advanced2 and Academic groups on either of these measures, however there were clear differences between this group and the Introductory and Standard groups, with the former exhibiting clearly superior accuracy. While time records were taken approximately, so as to avoid adding time pressure as a variable, that the Advanced1, Advanced2 and Academic groups recorded more time in their consideration of the problems, may suggest a “pause and consider” approach to such problems is a characteristic of the advanced groups. This is in line with what was suggested by an eye-movement tracking study of mathematically trained students attempting the Four Cards Problem; where participants that had not chosen the standard error had spent longer considering the card linked to the matching bias effect [ 14 ]. It is important to note, however, that longer response times may reflect other cognitive processes than deliberation [ 32 ].
Performance on some problems was associated with performance on other problems. That is, if someone correctly answered a problem in one of these sets, they were also highly likely to correctly answer the other problems in the set. These sets were: (1) Lily Pads, Widgets and Petrol Station; (2) Hospitals, Four Cards and Two Drivers; (3) Birth Order and Coin Tosses. This is different with how these problems have been typically clustered a priori in the research literature: (I) Lily Pads, Widgets and Bat and Ball (CRT); (II) Hospitals and Two Drivers (explained below); (III) Hospitals, Birth Order and Coin Tosses (representativeness heuristic); (IV) Birth Order and Coin Tosses (probability theory). Consideration of these problem groupings follows.
Correctly answering all three problems in (I) entailed not being distracted by particular pieces of information in the problems so as to stay focused on uncovering the real underlying relationships. The Lily Pads and Widget problems can mislead if attention is over focused on the numbers, and conversely, the Petrol Station problem can mislead if there is too much focus on the idea of a discount. While the Lily Pads and Widget problems are traditionally paired with the Bat and Ball problem in the CRT, it may be that performance on the Bat and Ball problem did not appear as part of this set due to an added level of difficulty. With the problems in (I), avoiding being distracted by certain parts of the questions at the expense of others almost leads directly to the correct answer. However, with the Bat and Ball problem, further steps in mathematical reasoning still need to occur in answering which two numbers add together to give a result while also subtracting one from the other for another.
With the problems in (II) it is of interest that the Two Drivers problem was created specifically to be paired with the Hospitals problem to test for motivation in problem solving [ 23 ]. Within this framework further transparent versions of these problems were successfully devised to manipulate for difficulty. The Two Drivers problem was amended to have Driver B travelling at exactly 5 mph during the first half of the race and at exactly 95 mph during the last half of the race. The Hospitals problem was amended so the smaller hospital would have “only 2” babies born each day and where for a period of one year the hospitals recorded the number of days on which all of the babies born were boys. Could the association in (II) be pointing to how participants overcome initial fictitious mathematical rules? Maybe they reframe the question in simpler terms to see the pattern. The Four Cards Problem also elicited a high number of incorrect answers where, associated with mathematical training, the standard incorrect solution was avoided for more cognitively elaborate ones. Indeed, a gradation effect appeared across the groups where the standard error of the “D and 3” cards becomes “D only” ( Table 4 ). Adrian Simpson and Derrick Watson found a comparable result across their two groups [14 p61]. This could again be pointing to having avoided an initial fictitious rule of simply concentrating on items directly found in the question, participants then seek to reframe the question to unearth the logical rule to be deduced. An added level of difficulty with this question may be why participants become trapped in a false answer. The eye-movement tracking study mentioned above supports this theory.
| Introductory | Standard | Advanced1 | Advanced2 | Academic | |
|---|---|---|---|---|---|
| Errors Total N (%) | 59 (95%) | 26 (96%) | 30 (85%) | 27 (61%) | 19 (63%) |
| Standard Error | 49% | 42% | 23% | 30% | 11% |
| “D only” Error | 20% | 27% | 40% | 26% | 53% |
| Other Error | 31% | 31% | 37% | 44% | 37% |
The problems in (III) fit naturally together as part of basic probability theory, a topic participants would have assimilated, or not, as part of various education curricula. While the equal likelihood of all possible outcomes with respect to a coin toss may be culturally assimilated, the same may not be as straightforward for birth gender outcomes where such assumptions could be swayed by biological hypothesis or folk wisdom [ 33 ]. The gradation of the results in terms of mathematical training does not support this possibility.
The effect of training on performance accuracy was more obvious in some problems compared to others, and to some extent, this was related to the type of problem. For instance, most of the problems in which performance was related to training (Four Cards, CRT [Lily Pads, Widgets, Bat and Ball], Two Drivers, Jack looking at Anne) could be classed as relying on logical and/or critical thinking. The one exception was the Birth Order problems, which are probability related.
In contrast, two of the three problems in which training did not appear to have much impact on performance (Hospitals and Coin Tosses) require domain-specific knowledge. The Hospitals problem requires a degree of knowledge about sampling statistics. This is a topic of quite distinct flavour that not all mathematically trained individuals gain familiarity with. On the other hand, all groups having performed well on the Coin Tosses problem is in line with a level of familiarity with basic probability having been originally presented at high school. While the questioning of patterning as negatively correlated with randomness is similar to that appearing in the Birth Order question, in the Birth Order question this aspect is arguably more concealed. These results and problem grouping (III) could be pointing to an area for improvement in teaching where the small gap in knowledge required to go from answering the Coin Tosses problem correctly to achieving similarly with the Birth Order problem could be easily addressed. A more formal introduction to sampling statistics in mathematical training could potentially bridge this gap as well as further be extended towards improvement on the Hospitals problem.
The other problem where performance was unrelated to training, the Petrol Station problem, cannot be characterised similarly. It is more of a logical/critical thinking type problem, where there remains some suggestion that training may have impacted performance, as the Academic group seemed to perform better than the rest of the sample. An alternate interpretation of this result is therefore that this problem should not be isolated but grouped with the other problems where performance is affected by training.
Although several aspects of the data suggest mathematics training improves the chances that someone will solve problems of the sort examined here, differences in the performance of participants in the Advanced1, Advanced2 and Academic groups were not obvious. This is despite the fact that large differences exist in the amount of training in these three groups. The first two groups were undergraduate students and the Academic group all had PhDs and many were experienced academic staff. One interpretation of this result is current mathematics training can only take someone so far in terms of improving their abilities with these problems. There is a point of demarcation to consider in terms of mathematical knowledge between the Advanced1, Advanced2 and Academic groups as compared to the Introductory and Standard groups. In Australia students are able to drop mathematical study at ages 15–16 years, or choose between a number of increasingly involved levels of mathematics. For the university in this study, students are filtered upon entry into mathematics courses according to their current knowledge status. All our groups involved students who had opted for post-compulsory mathematics at high school. And since our testing occurred in second semester, some of the mathematical knowledge shortfalls that were there upon arrival were bridged in first semester. Students must pass a first semester course to be allowed entry into the second semester course. A breakdown of the mathematics background of each group is as follows:
- The Introductory group’s mathematics high school syllabus studied prior to first semester course entry covered: Functions, Trigonometric Functions, Calculus (Introduction to Differentiation, Applications of the Derivative, Antiderivatives, Areas and the Definite Integral), Financial Mathematics, Statistical Analysis. The Introductory group then explored concepts in mathematical modelling with emphasis on the importance of calculus in their first semester of mathematical studies.
- The Standard group’s mathematics high school syllabus studied prior to first semester course entry covered: Functions, Trigonometric Functions, Calculus (Rates of Change, Integration including the method of substitution, trigonometric identities and inverse trigonometric functions, Areas and Volumes of solids of revolution, some differential equations), Combinatorics, Proof (with particular focus on Proof by Mathematical Induction), Vectors (with application to projectile motion), Statistical Analysis. In first semester their mathematical studies then covered a number of topics the Advanced1 group studied prior to gaining entrance at university; further details on this are given below.
- The Advanced1 group’s mathematics high school syllabus studied prior to first semester course entry covered: the same course content the Standard group covered at high school plus extra topics on Proof (develop rigorous mathematical arguments and proofs, specifically in the context of number and algebra and further develop Proof by Mathematical Induction), Vectors (3 dimensional vectors, vector equations of lines), Complex Numbers, Calculus (Further Integration techniques with partial fractions and integration by parts), Mechanics (Application of Calculus to Mechanics with simple harmonic motion, modelling motion without and with resistance, projectiles and resisted motion). The Standard group cover these topics in their first semester university studies in mathematics with the exclusion of further concepts of Proof or Mechanics. In first semester the Advanced1 group have built on their knowledge with an emphasis on both theoretical and foundational aspects, as well as developing the skill of applying mathematical theory to solve practical problems. Theoretical topics include a host of theorems relevant to the study of Calculus.
In summary, at the point of our study, the Advanced1 group had more knowledge and practice on rigorous mathematical arguments and proofs in the context of number and algebra, and more in-depth experience with Proofs by Induction, but the bulk of extra knowledge rests with a much deeper knowledge of Calculus. They have had longer experience with a variety of integration techniques, and have worked with a variety of applications of calculus to solve practical problems, including a large section on mechanics at high school. In first semester at university there has been a greater focus on theoretical topics including a host of theorems and associated proofs relevant to the topics studied. As compared to the Introductory and Standard groups, the Advanced1 group have only widened the mathematics knowledge gap since their choice of post-compulsory mathematics at high school. The Advanced2 group come directly from an Advanced1 cohort. And the Academics group would have reached the Advanced1 group’s proficiency as part of their employment. So, are specific reasoning skills resulting from this level of abstract reasoning? Our findings suggest this should certainly be an area of investigation and links in interestingly with other research work. In studying one of the thinking tasks in particular (the Four Cards Problem) and its context of conditional inference more specifically, Inglis and Simpson [ 15 ] found a clear difference between undergraduates in mathematics and undergraduates in other university disciplines, yet also showed a lack of development over first-year university studies on conditional inference measures. A follow up study by Attridge and Inglis [ 22 ] then zeroed in on post-compulsory high school mathematical training and found that students with such training did develop their conditional reasoning to a greater extent than their control group over the course of a year, despite them having received no explicit tuition in conditional logic. The development though, whilst demonstrated as not being the result of a domain-general change in cognitive capacity or thinking disposition, and most likely associated with the domain-specific study of mathematics, revealed a complex pattern of endorsing more of some inferences and less of others. The study here focused on a much broader problem set associated with logical and critical thinking and it too is suggestive of a more complex picture in how mathematics training may be contributing to problem solving styles. A more intricate pattern to do with the impact of mathematical training on problem solving techniques is appearing as required for consideration.
There is also a final interpretation to consider: that people in the Advanced 1, Advanced2 and Academic groups did not gain anything from their mathematics training in terms of their ability to solve these problems. Instead, with studies denying any correlation of many of these problems with what is currently measured as intelligence [ 30 ], they might still be people of a particular intelligence or thinking disposition to start with, who have been able to use that intelligence to not only solve these problems, but also survive the challenges of their mathematics training.
That the CRT has been traditionally used as a measure of baseline thinking disposition and that performance has been found to be immutable across groups tested is of particular interest since our results show a clear possible training effect on these questions. CRT is tied with a willingness to engage in effortful thinking which presents as a suitable ability for training. It is beyond the scope of this study, but a thorough review of CRT testing is suggestive of a broader appreciation and better framework to understand thinking disposition, ability and potential ability.
Mathematical training appears associated with certain thinking skills, but there are clearly some subtleties that need to be extricated. The thinking tasks here add to the foundational results where the aim is for a firmer platform on which to eventually base more targeted and illustrative inquiry. If thinking skills can be fostered, could first year university mathematics teaching be improved so that all samples from that group reach the Advanced1 group level of reasoning? Do university mathematics courses become purely about domain-specific knowledge from this point on? Intensive training has been shown to impact the brain and cognition across a number of domains from music [ 34 ], to video gaming [ 35 ], to Braille reading [ 36 ]. The hypothesis that mathematics, with its highly specific practice, fits within this list remains legitimate, but simply unchartered. With our current level of understanding it is worth appreciating the careful wording of the NYU Courant Institute on ‘Why Study Math?’ where there is no assumption of causation: “Mathematicians need to have good reasoning ability in order to identify, analyze, and apply basic logical principles to technical problems.” [ 37 ].
Limitations
One possible limitation of the current study is that the problems may have been too easy for the more advanced people, and so we observed a ceiling effect (i.e., some people obtained 100% correct on all problems). This was most obvious in the Advanced1, Advanced2 and Academic groups. It is possible that participants in these groups had developed logical and critical thinking skills throughout their mathematical training that were sufficient to cope with most of the problems used in this study, and so this would support the contention that training in mathematics leads to the development of logical and critical thinking skills useful in a range of domains. Another interpretation is that participants in these groups already possessed the necessary thinking skills for solving the problems in this study, which is why they are able to cope with the material in the advanced units they were enrolled in, or complete a PhD in mathematics and hold down an academic position in a mathematics department. This would then suggest that training in mathematics had no effect on abstract thinking skills—people in this study possessed them to varying extents prior to their studies. This issue might be settled in a future study that used a greater number of problems of varying difficulties to maximise the chances of finding a difference between the three groups with the most amount of training. Alternatively, a longitudinal study that followed people through their mathematics training could determine whether their logical and critical thinking abilities changed throughout their course.
A further limitation of the study may be that several of the reasoning biases examined in this study were measured by only one problem each (i.e., Four Cards Problem, Two Drivers, Petrol Station, Jack looking at Anne). A more reliable measure of these biases could be achieved by including more problems that tap into these biases. This would, however, increase the time required of participants during data collection, and in the context of this study, would mean a different mode of testing would likely be required.
Broad sweeping intuitive claims of the transferable skills endowed by a study of mathematics require evidence. Our study uniquely covers a wide range of participants, from limited mathematics training through to research academics in the mathematical sciences. It furthermore considered performance on 11 well-studied thinking tasks that typically elude participants in psychological studies and on which results have been uncorrelated with general intelligence, education levels and other demographic information [ 15 , 16 , 30 ]. We identified different performances on these tasks with respect to different groups, based on level of mathematical training. This included the CRT which has developed into a method of measuring baseline thinking disposition. We identified different distributions of types of errors for the mathematically trained. We furthermore identified a performance threshold that exists in first year university for those with high level mathematics training. This study then provides insight into possible changes and adjustments to mathematics courses in order for them to fulfil their advertised goal of reaching improved rational and logical reasoning for a higher number of students.
It is central to any education program to have a clear grasp of the nature of what it delivers and how, but arguably especially so for the core discipline that is mathematics. In 2014 the Office of The Chief Scientist of Australia released a report “Australia’s STEM workforce: a survey of employers” where transferable skills attributed to mathematics were also ones that employers deemed as part of the most valuable [ 38 ]. A better understanding of what mathematics delivers in this space is an opportunity to truly capitalise on this historical culture-crossing subject.
Supporting information
Acknowledgments.
The authors would like to thank Jacqui Ramagge for her proof reading and input, as well as support towards data collection.
Funding Statement
The authors received no specific funding for this work.
Data Availability
- PLoS One. 2020; 15(7): e0236153.
Decision Letter 0
17 Mar 2020
PONE-D-20-01159
Does mathematics training lead to better logical thinking and reasoning? A cross-sectional assessment from students to professors
Dear Professor Speelman,
Thank you for submitting your manuscript to PLOS ONE. I have sent it to two expert reviewers and have received their comments back. As you can see at the bottom of this email, both reviewers are positive about your manuscript but raise some issues that you would need to address before the manuscript can be considered for publication. Notably, reviewer #1 points out that the manuscript should include a discussion on the reasons why individuals with math training may have improved reasoning skills (e.g., logical intuitions versus deliberate thinking). The reviewer also rightly mentions that your sample sizes are limited, notably for the most advanced groups. This should be discussed and acknowledged. Reviewer #2 has a number of conceptual and methodological points that you will also have to address. The reviewer provides very thorough comments and I will not reiterate the points here. However, note that both reviewers suggest that you need to improve the figures and I agree with them.
We would appreciate receiving your revised manuscript by May 01 2020 11:59PM. When you are ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.
If you would like to make changes to your financial disclosure, please include your updated statement in your cover letter.
To enhance the reproducibility of your results, we recommend that if applicable you deposit your laboratory protocols in protocols.io, where a protocol can be assigned its own identifier (DOI) such that it can be cited independently in the future. For instructions see: http://journals.plos.org/plosone/s/submission-guidelines#loc-laboratory-protocols
Please include the following items when submitting your revised manuscript:
- A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). This letter should be uploaded as separate file and labeled 'Response to Reviewers'.
- A marked-up copy of your manuscript that highlights changes made to the original version. This file should be uploaded as separate file and labeled 'Revised Manuscript with Track Changes'.
- An unmarked version of your revised paper without tracked changes. This file should be uploaded as separate file and labeled 'Manuscript'.
Please note while forming your response, if your article is accepted, you may have the opportunity to make the peer review history publicly available. The record will include editor decision letters (with reviews) and your responses to reviewer comments. If eligible, we will contact you to opt in or out.
We look forward to receiving your revised manuscript.
Kind regards,
Jérôme Prado
Academic Editor
Journal Requirements:
When submitting your revision, we need you to address these additional requirements:
1. Please ensure that your manuscript meets PLOS ONE's style requirements, including those for file naming. The PLOS ONE style templates can be found at http://www.plosone.org/attachments/PLOSOne_formatting_sample_main_body.pdf and http://www.plosone.org/attachments/PLOSOne_formatting_sample_title_authors_affiliations.pdf
2. Please include additional information regarding the survey or questionnaire used in the study and ensure that you have provided sufficient details that others could replicate the analyses. For instance, if you developed a questionnaire as part of this study and it is not under a copyright more restrictive than CC-BY, please include a copy, in both the original language and English, as Supporting Information. Please also let us know if it would be possible to provide the anonymized data points necessary to replicate the statistical analyses, for instance, as shown in fig 1 and 2. If so, please deposit those to a suitable data repository or include them in the Supporting Information files.
3. Thank you for stating the following financial disclosure:
"The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript."
- Please provide an amended Funding Statement that declares *all* the funding or sources of support received during this specific study (whether external or internal to your organization) as detailed online in our guide for authors at http://journals.plos.org/plosone/s/submit-now .
- Please state what role the funders took in the study. If any authors received a salary from any of your funders, please state which authors and which funder. If the funders had no role, please state: "The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript."
Please include your amended statements within your cover letter; we will change the online submission form on your behalf.
[Note: HTML markup is below. Please do not edit.]
Reviewers' comments:
Reviewer #1: I think this is a very good and interesting manuscript trying to answer an important research question. I propose some changes that I believe should be applied before publication.
1. Each reasoning bias is measured with only one problem. In reasoning research, it is rather common to measure each type of reasoning problem with a series of structurally equivalent reasoning problems, so the results will be independent of contexts effects and will be generalizable to that type of problem. Here, the authors only measured each reasoning bias with one single problem and this might be problematic (see, for example: Fiedler & Hertel, 1994). I think this can be addressed by simply discussing it in the limitation section.
2. This is rather a minor issue, but the discussion on the CRT problems is not up-to-date (page 7). Most recent experiments on dual process theory suggest that people who are able to correctly solve these reasoning problems (including the CRT) do so intuitively, and not because they engaged in careful deliberation (Bago & De Neys, 2019). Intelligence made people have better intuitive responses (Thompson, Pennycook, Trippas & Evans, 2018). Similarly, this problems persists in the discussion about reaction times (page 25). Longer reaction times does not necessarily mean that people engaged in deliberation (see: Evans, Kyle, Dillon & Rand, 2015). Response time might be driven by decision conflict or response rationalization. These issues could be clarified with some changes in the wording or some footnotes on page 7 and 25. Furthermore, it would be interesting to have a discussion on how mathematical education helps people overcome their biases. Is it because it creates better intuition, or helps people engage in deliberation? An interesting question this manuscript does not discuss. It’s on the authors whether or not they discuss this latter point now, but the changes on page 7 and 25 should be made.
3. A more serious problem is the rather small sample size (especially in the more advanced groups). This small sample size makes the appearance of both false negatives and false positives more likely. Perhaps, the authors could compute the Bayes Factors for the chi-square or logistic regression test, so we can actually see how strong the evidence is for or against the null. This is especially important as the authors run a great number of explorative analysis (Table 3), and some of those results might need to be interpreted with great caution (depending on the Bayes Factor).
The graphs are not looking good, they should comply with APA formatting. At the very least, the axis titles should be meaningful and measure units should be written there.
The presentation order of the problems is quite unusual; why isn’t it random? Why did the authors decide on this order?
Reviewer #2: The study reported in this paper compared five groups of participants with varying levels of mathematical expertise on a set of reasoning tasks. The study is interesting and informative. It extends the current literature on this topic (which is reviewed very nicely in the introduction). However, there are some issues with the current analysis and interpretation that should be resolved prior to publication. I have therefore recommended major revisions. My comments are organised in the order in which they came up in the paper and they explain my responses to the questions above.
1. Line 114 – “general population” a bit misleading – they were also students but from other disciplines.
2. Line 124 onwards reads:
“The ultimate question to consider here is: are any skills associated with mathematics training innate or do they arise from skills transfer? Though to investigate how mathematical training affects reasoning skills, randomised sampling and randomised intervention to reveal causal relationships are clearly not viable. With so many possible confounding variables and logistical issues, it is even questionable what conclusions such studies might provide. Furthermore, a firm baseline from which to propose more substantive investigations is still missing.”
I find this paragraph slightly problematic because the current study doesn’t inform us on this ultimate question, so it makes the outline of the current study in the following paragraph feel unsatisfactory. I think the current study is important but prefacing it with this paragraph underplays that importance. And I think a randomised controlled study, although not viable, would give the answers we need because the random allocation to groups would allow us to rule out any confounding variables. Finally, the last sentence in this paragraph is unclear to me.
3. In the descriptions of the five participants groups the authors refer to the group’s level of interest in mathematics, but this seems like an overgeneralisation to me. Surely the introductory group could contain a biology student who also happens to be good at mathematics and very much enjoy it? I would be more comfortable with the descriptions if the parts about interest level were removed.
4. How many of the 123 first year students were in each of the three first year groups?
5. Line 313 – the standard group is referred to as “university mathematics students”, but they are not taking mathematics degreed.
6. Line 331 - what is a practice class?
7. Were the data collection settings quiet? From the description it sounds like groups of participants were completing the study at the same time in the same room, but the authors should make this explicit for the sake of the method being reproducible. E.g. how many students were in the room at the time?
8. Line 355-356 – the authors should not use the term “marginally worse” because this is statistically inappropriate – in a frequentist approach results are either significant or non-significant.
9. Line 340 – “approximate completion times were noted.”
This doesn’t sound rigorous enough to justify analysing them. Their analysis is interesting, but the authors should remind readers clearly whenever the response times are analysed or discussed that their recording was only manual and approximate.
10. I suggest replacing Figure 1 with a bar chart showing standard error of the mean on the error bars. A table with mean score out of 11 and the standard deviation for each group may also be useful. Figure 2 should be a scatterplot rather than a box and whisker plot.
11. Was the 0-11 total correct score approximately normally distributed across the full sample?
12. Chi square analysis requires at least 5 cases in each cell, was this met? It seems not since Table 1 shows lots of cells in the “no response” row having 0% of cases.
13. The chi-square analyses should be followed up with post hoc tests to see exactly where the differences between groups are. The descriptions as they stand aren’t that informative (as readers can just look at Table 1) without being backed up by post hoc tests.
14. For each chi square analysis in the text, I would find it easier to read if the test statistics came at the top of the paragraph, before the description.
15. Line 381-383 – “Of note, also, is the relatively low proportion of those in the higher training groups who, when they made an error, did not make the standard error, a similar result to the one reported by Inglis and Simpson [11]."
I think this is supposed to say that a low proportion did make the standard error or that a high proportion did not make the standard error.
16. Line 403 - p values this small should be reported as p < .001 rather than p = .000 since they aren’t actually 0.
17. Line 476 – “…if a particular outcome variable was predicted significantly by a particular predictor variable, the converse relationship was also observed”
Isn’t that necessarily the case with regression analyses, like with correlations?
18. I don’t think the logistic regression analyses add much to the paper and at the moment they come across as potential p-hacking since they don’t clearly relate to the research question. To me they make the paper feel less focused. Having said that, there is some interesting discussion of them in the Discussion section. I’d recommend adding some justification to the introduction for why it is interesting to look at the relationships among tasks (without pretending to have made any specific hypotheses about the relationships, of course).
19. Line 509 would be clearer if it read “between these groups and the introductory and standard groups”
20. Lines 597 – 620 - This is an interesting discussion, especially the suggestion that advanced calculus may be responsible for the development. No development in reasoning skills from the beginning of a mathematics degree onwards was also found by Inglis and Simpson (2009), who suggested that the initial difference between mathematics and non-mathematics undergraduates could have been due to pre-university study of mathematics. Attridge & Inglis (2013) found evidence that this was the case (they found no difference between mathematics and non-mathematics students at age 16 but a significant difference at the end of the academic year, where the mathematics students had improved and the non-mathematics students had not).
Could the authors add some discussion of whether something similar may have been the case with their Australian sample? E.g. do students in Australia choose whether, or to what extent, to study mathematics towards the end of high school? If not, the description of the groups suggests that there were at least differences in high school mathematics attainment between groups 1-3, even if they studied the same mathematics curriculum. Do the authors think that this difference in attainment could have led to the differences between groups in the current study?
21. Line 617 – “Intensive training has been shown to impact the brain and cognition across a number of domains from music, to video gaming, to Braille reading [31].”
Reference 31 appears to only relate to music. Please add references for video gaming and Braille reading.
22. I recommend editing the figures from SPSS’s default style or re-making them in Excel or DataGraph to look more attractive.
23. I cannot find the associated datafile anywhere in the submission. Apologies if this is my mistake.
[NOTE: If reviewer comments were submitted as an attachment file, they will be attached to this email and accessible via the submission site. Please log into your account, locate the manuscript record, and check for the action link "View Attachments". If this link does not appear, there are no attachment files to be viewed.]
While revising your submission, please upload your figure files to the Preflight Analysis and Conversion Engine (PACE) digital diagnostic tool, https://pacev2.apexcovantage.com/ . PACE helps ensure that figures meet PLOS requirements. To use PACE, you must first register as a user. Registration is free. Then, login and navigate to the UPLOAD tab, where you will find detailed instructions on how to use the tool. If you encounter any issues or have any questions when using PACE, please email us at gro.solp@serugif . Please note that Supporting Information files do not need this step.
Author response to Decision Letter 0
20 Apr 2020
All responses are detailed against the specific reviewers' comments in the Response to Reviewers document
Submitted filename: Response to Reviewers.docx
Decision Letter 1
11 Jun 2020
PONE-D-20-01159R1
Does mathematics training lead to better logical thinking and reasoning? A cross-sectional assessment from students to professors.
Dear Dr. Speelman,
Thank you for submitting your revised manuscript to PLOS ONE. I have sent it to reviewer #2 and have now received the reviewer's comment. As you can see, the reviewer thinks that the manuscript is improved but has some outstanding issues that you would need to address in another round of revision. I notably agree with the reviewer that you should provide the raw data, allowing readers to replicate your analyses. Therefore, I invite you submit a revised version of your manuscript.
Please submit your revised manuscript by Jul 26 2020 11:59PM. If you will need more time than this to complete your revisions, please reply to this message or contact the journal office at gro.solp@enosolp . When you're ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.
- A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). You should upload this letter as a separate file labeled 'Response to Reviewers'.
- A marked-up copy of your manuscript that highlights changes made to the original version. You should upload this as a separate file labeled 'Revised Manuscript with Track Changes'.
- An unmarked version of your revised paper without tracked changes. You should upload this as a separate file labeled 'Manuscript'.
If you would like to make changes to your financial disclosure, please include your updated statement in your cover letter. Guidelines for resubmitting your figure files are available below the reviewer comments at the end of this letter.
If applicable, we recommend that you deposit your laboratory protocols in protocols.io to enhance the reproducibility of your results. Protocols.io assigns your protocol its own identifier (DOI) so that it can be cited independently in the future. For instructions see: http://journals.plos.org/plosone/s/submission-guidelines#loc-laboratory-protocols
Reviewer #2: The manuscript has improved but there are still a few issues that should be resolved prior to publication.
1. On lines 96, 97, 100 and 102, the references to “general population” should be changed to reflect the fact that these participants were non-mathematics (arts) students.
2. Line 306 – change “mathematics students” to “university students”.
3. The method section doesn’t specify the gender split and mean age of the sample.
4. Table 3 - values the p values listed as .000 should be changed to <.001.
5. Table 3 - I suggest repeating the list of problem numbers and names in the legend. It may make for a long legend but would make it much easier for the reader to interpret the table.
6. I am not sure what the new post hoc tests are comparing. What I expected was to see group 1 compared to groups 2, 3, 4 and 5, and so on. This would tell us which groups are statistically different from each other. At the moment we only know from the overall chi square tests whether there are any differences among the groups or not, we don’t know specifically which groups are statistically different from each other and which ones are not. We only have the authors’ interpretations based on the observed counts.
7. Line 584 - change “performance was correlated with training” to “performance was related to training” to avoid any confusion since a correlation analysis was not performed.
8. Data file – I had expected the data file to give the raw data rather than summary data, i.e. with each participant in a separate row, and a column indicating their group membership, a column giving their age, a column for sex etc (including all the demographics mentioned in the method), and a column for each reasoning question. This would allow other researchers to replicate the regression analyses and look at other relationships within the dataset. Without being able to replicate all analyses in the paper, the data file does not meet the minimal data set definition for publication in PLOS journals: https://journals.plos.org/plosone/s/data-availability .
[NOTE: If reviewer comments were submitted as an attachment file, they will be attached to this email and accessible via the submission site. Please log into your account, locate the manuscript record, and check for the action link "View Attachments". If this link does not appear, there are no attachment files.]
While revising your submission, please upload your figure files to the Preflight Analysis and Conversion Engine (PACE) digital diagnostic tool, https://pacev2.apexcovantage.com/ . PACE helps ensure that figures meet PLOS requirements. To use PACE, you must first register as a user. Registration is free. Then, login and navigate to the UPLOAD tab, where you will find detailed instructions on how to use the tool. If you encounter any issues or have any questions when using PACE, please email PLOS at gro.solp@serugif . Please note that Supporting Information files do not need this step.
Author response to Decision Letter 1
16 Jun 2020
Please see "Response to Reviewers" document
Decision Letter 2
PONE-D-20-01159R2
We’re pleased to inform you that your manuscript has been judged scientifically suitable for publication and will be formally accepted for publication once it meets all outstanding technical requirements.
Within one week, you’ll receive an e-mail detailing the required amendments. When these have been addressed, you’ll receive a formal acceptance letter and your manuscript will be scheduled for publication.
An invoice for payment will follow shortly after the formal acceptance. To ensure an efficient process, please log into Editorial Manager at http://www.editorialmanager.com/pone/ , click the 'Update My Information' link at the top of the page, and double check that your user information is up-to-date. If you have any billing related questions, please contact our Author Billing department directly at gro.solp@gnillibrohtua .
If your institution or institutions have a press office, please notify them about your upcoming paper to help maximize its impact. If they’ll be preparing press materials, please inform our press team as soon as possible -- no later than 48 hours after receiving the formal acceptance. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information, please contact gro.solp@sserpeno .
Additional Editor Comments (optional):
Acceptance letter
Dear Dr. Speelman:
I'm pleased to inform you that your manuscript has been deemed suitable for publication in PLOS ONE. Congratulations! Your manuscript is now with our production department.
If your institution or institutions have a press office, please let them know about your upcoming paper now to help maximize its impact. If they'll be preparing press materials, please inform our press team within the next 48 hours. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information please contact gro.solp@sserpeno .
If we can help with anything else, please email us at gro.solp@enosolp .
Thank you for submitting your work to PLOS ONE and supporting open access.
PLOS ONE Editorial Office Staff
on behalf of
Dr. Jérôme Prado

How to Improve Problem-Solving Skills: Mathematics and Critical Thinking

In today’s rapidly changing world, problem-solving has become a quintessential skill. When we discuss the topic, it’s natural to ask, “What is problem-solving?” and “How can we enhance this skill, particularly in children?” The discipline of mathematics offers a rich platform to explore these questions. Through math, not only do we delve into numbers and equations, but we also explore how to improve problem-solving skills and how to develop critical thinking skills in math. Let’s embark on this enlightening journey together.
What is Problem-Solving?
At its core, problem-solving involves identifying a challenge and finding a solution. But it’s not always as straightforward as it sounds. So, what is problem-solving? True problem-solving requires a combination of creative thinking and logical reasoning. Mathematics, in many ways, embodies this blend. When a student approaches a math problem, they must discern the issue at hand, consider various methods to tackle it, and then systematically execute their chosen strategy.
But what is problem-solving in a broader context? It’s a life skill. Whether we’re deciding the best route to a destination, determining how to save for a big purchase, or even figuring out how to fix a broken appliance, we’re using problem-solving.
How to Develop Critical Thinking Skills in Math
Critical thinking goes hand in hand with problem-solving. But exactly how to develop critical thinking skills in math might not be immediately obvious. Here are a few strategies:
- Contextual Learning: Teaching math within a story or real-life scenario makes it relevant. When students see math as a tool to navigate the world around them, they naturally begin to think critically about solutions.
- Open-ended Questions: Instead of merely seeking the “right” answer, encourage students to explain their thought processes. This nudges them to think deeply about their approach.
- Group Discussions: Collaborative learning can foster different perspectives, prompting students to consider multiple ways to solve a problem.
- Challenging Problems: Occasionally introducing problems that are a bit beyond a student’s current skill level can stimulate critical thinking. They will have to stretch their understanding and think outside the box.
What are the Six Basic Steps of the Problem-Solving Process?
Understanding how to improve problem-solving skills often comes down to familiarizing oneself with the systematic approach to challenges. So, what are the six basic steps of the problem-solving process?
- Identification: Recognize and define the problem.
- Analysis: Understand the problem’s intricacies and nuances.
- Generation of Alternatives: Think of different ways to approach the challenge.
- Decision Making: Choose the most suitable method to address the problem.
- Implementation: Put the chosen solution into action.
- Evaluation: Reflect on the solution’s effectiveness and learn from the outcome.
By embedding these steps into mathematical education, we provide students with a structured framework. When they wonder about how to improve problem-solving skills or how to develop critical thinking skills in math, they can revert to this process, refining their approach with each new challenge.
Making Math Fun and Relevant
At Wonder Math, we believe that the key to developing robust problem-solving skills lies in making math enjoyable and pertinent. When students see math not just as numbers on a page but as a captivating story or a real-world problem to be solved, their engagement skyrockets. And with heightened engagement comes enhanced understanding.
As educators and parents, it’s crucial to continuously ask ourselves: how can we demonstrate to our children what problem-solving is? How can we best teach them how to develop critical thinking skills in math? And how can we instill in them an understanding of the six basic steps of the problem-solving process?
The answer, we believe, lies in active learning, contextual teaching, and a genuine passion for the beauty of mathematics.
The Underlying Beauty of Mathematics
Often, people perceive mathematics as a rigid discipline confined to numbers and formulas. However, this is a limited view. Math, in essence, is a language that describes patterns, relationships, and structures. It’s a medium through which we can communicate complex ideas, describe our universe, and solve intricate problems. Understanding this deeper beauty of math can further emphasize how to develop critical thinking skills in math.
Why Mathematics is the Ideal Playground for Problem-Solving
Math provides endless opportunities for problem-solving. From basic arithmetic puzzles to advanced calculus challenges, every math problem offers a chance to hone our problem-solving skills. But why is mathematics so effective in this regard?
- Structured Challenges: Mathematics presents problems in a structured manner, allowing learners to systematically break them down. This format mimics real-world scenarios where understanding the structure of a challenge can be half the battle.
- Multiple Approaches: Most math problems can be approached in various ways . This teaches learners flexibility in thinking and the ability to view a single issue from multiple angles.
- Immediate Feedback: Unlike many real-world problems where solutions might take time to show results, in math, students often get immediate feedback. They can quickly gauge if their approach works or if they need to rethink their strategy.
Enhancing the Learning Environment
To genuinely harness the power of mathematics in developing problem-solving skills, the learning environment plays a crucial role. A student who is afraid of making mistakes will hesitate to try out different approaches, stunting their critical thinking growth.
However, in a nurturing, supportive environment where mistakes are seen as learning opportunities, students thrive. They become more willing to take risks, try unconventional solutions, and learn from missteps. This mindset, where failure is not feared but embraced as a part of the learning journey, is pivotal for developing robust problem-solving skills.
Incorporating Technology
In our digital age, technology offers innovative ways to explore math. Interactive apps and online platforms can provide dynamic problem-solving scenarios, making the process even more engaging. These tools can simulate real-world challenges, allowing students to apply their math skills in diverse contexts, further answering the question of how to improve problem-solving skills.
More than Numbers
In summary, mathematics is more than just numbers and formulas—it’s a world filled with challenges, patterns, and beauty. By understanding its depth and leveraging its structured nature, we can provide learners with the perfect platform to develop critical thinking and problem-solving skills. The key lies in blending traditional techniques with modern tools, creating a holistic learning environment that fosters growth, curiosity, and a lifelong love for learning.
Join us on this transformative journey at Wonder Math. Let’s make math an adventure, teaching our children not just numbers and equations, but also how to improve problem-solving skills and navigate the world with confidence. Enroll your child today and witness the magic of mathematics unfold before your eyes!
FAQ: Mathematics and Critical Thinking
1. what is problem-solving in the context of mathematics.
Problem-solving in mathematics refers to the process of identifying a mathematical challenge and systematically working through methods and strategies to find a solution.
2. Why is math considered a good avenue for developing problem-solving skills?
Mathematics provides structured challenges and allows for multiple approaches to find solutions. This promotes flexibility in thinking and encourages learners to view problems from various angles.
3. How does contextual learning enhance problem-solving abilities?
By teaching math within a story or real-life scenario, it becomes more relevant for the learner. This helps them see math as a tool to navigate real-world challenges , thereby promoting critical thinking.
4. What are the six basic steps of the problem-solving process in math?
The six steps are: Identification, Analysis, Generation of Alternatives, Decision Making, Implementation, and Evaluation.
5. How can parents support their children in developing mathematical problem-solving skills?
Parents can provide real-life contexts for math problems , encourage open discussions about different methods, and ensure a supportive environment where mistakes are seen as learning opportunities.
6. Are there any tools or apps that can help in enhancing problem-solving skills in math?
Yes, there are various interactive apps and online platforms designed specifically for math learning. These tools provide dynamic problem-solving scenarios and simulate real-world challenges, making the learning process engaging.
7. How does group discussion foster critical thinking in math?
Group discussions allow students to hear different perspectives and approaches to a problem. This can challenge their own understanding and push them to think about alternative methods.
8. Is it necessary to always follow the six steps of the problem-solving process sequentially?
While the six steps provide a structured approach, real-life problem-solving can sometimes be more fluid. It’s beneficial to know the steps, but adaptability and responsiveness to the situation are also crucial.
9. How does Wonder Math incorporate active learning in teaching mathematics?
Wonder Math integrates mathematics within engaging stories and real-world scenarios, making it fun and relevant. This active learning approach ensures that students are not just passive recipients but active participants in the learning process.
10. What if my child finds a math problem too challenging and becomes demotivated?
It’s essential to create a supportive environment where challenges are seen as growth opportunities. Remind them that every problem is a chance to learn, and it’s okay to seek help or approach it differently.
Related posts

Summer Math Programs: How They Can Prevent Learning Loss in Young Students
As summer approaches, parents and educators alike turn their attention to how they can support young learners during the break. Summer is a time for relaxation, fun, and travel, yet it’s also a critical period when learning loss can occur. This phenomenon, often referred to as the “summer slide,” impacts students’ progress, especially in foundational subjects like mathematics. It’s reported…
Math Programs 101: What Every Parent Should Know When Looking For A Math Program
As a parent, you know that a solid foundation in mathematics is crucial for your child’s success, both in school and in life. But with so many math programs and math help services out there, how do you choose the right one? Whether you’re considering Outschool classes, searching for “math tutoring near me,” or exploring tutoring services online, understanding…
- Bachelor of Arts Degree in Early Childhood Education (BAECE)
- Bachelor of Arts in Early Childhood Development with an Inspired Teaching and Learning Preliminary Multiple Subject Teaching Credential (California)
- Bachelor of Arts in English
- Bachelor of Arts in History
- Master of Arts in Social Emotional Learning
- Master of Education in Inspired Teaching and Learning with a Preliminary Multiple and Single Subject Teaching Credential and Intern Option (CA)
- Master of Arts in Education
- Master of Early Childhood Education
- Education Specialist
- Doctor of Education
- Doctor of Philosophy in Education
- Doctor of Education in Educational Leadership
- Ed.D. in Organizational Innovation
- Certificate in Online Teaching (COT) Program
- Online Medical Coding Program
- Building Our Team Through Community Policing
- Inspired Teaching and Learning with a Preliminary Single Subject Teaching Credential
- Inspired Teaching and Learning with a Preliminary Multiple Subject Teaching Credential and Internship Option (California)
- Preliminary Administrative Services Credential (CA Option)
- Preliminary Education Specialist Credential: Mild/Moderate with Internship Option (CA)
- All Teaching & Education
- Associate of Science in Business
- Bachelor of Business Administration
- Bachelor of Science in Healthcare Administration
- Bachelor of Arts in Management
- Master of Business Administration (MBA)
- Master of Public Health (MPH)
- Master of Science in Data Science
- Master of Public Administration
- Doctor of Criminal Justice
- Doctor of Philosophy in Organizational Leadership
- Doctor of Business Administration
- Doctor of Philosophy in Business Administration
- Post-Baccalaureate Certificate in Business
- Post-Master's Certificate in Business
- Graduate Certificate in Banking
- Certificate in Agile Project Management
- All Business & Marketing
- Bachelor of Science in Nursing (BSN) (California)
- Bachelor of Science in Nursing (BSN) Second Bachelor Degree (California)
- Bachelor of Science in Clinical Laboratory Science
- Bachelor of Science in Public Health
- Master of Science in Nursing
- Master of Science in Health Informatics
- Master of Healthcare Administration
- Doctor of Nurse Anesthesia Practice (DNAP)
- Doctor of Health Administration
- Doctor of Nursing Practice in Executive Leadership
- LVN to RN 30 Unit Option Certificate
- Psychiatric Mental Health Nurse Practitioner Certificate
- Family Nurse Practitioner Certificate
- Emergency Medical Technician Certificate
- All Healthcare & Nursing
- Bachelor of Arts in Psychology
- Bachelor of Arts in Integrative Psychology
- Bachelor of Science in Criminal Justice Administration
- Bachelor of Arts in Sociology
- Master of Science in Applied Behavioral Analysis Degree
- Master of Arts Degree in Counseling Psychology
- Master of Arts in Consciousness, Psychology, and Transformation
- Doctor of Clinical Psychology (PsyD) Program
- Doctor of Philosophy in Marriage and Family Therapy
- Doctor of Philosophy in Psychology
- Doctorate of Marriage and Family Therapy
- Graduate Certificate in Trauma Studies
- Post-Master's Certificate in Psychology
- Post-Baccalaureate Certificate in Applied Behavior Analysis
- Pupil Personnel Services Credential School Counseling (PPSC)
- University Internship Credential Program for Pupil Personnel Services School Counseling (California Only)
- All Social Sciences & Psychology
- Bachelor of Science in Cybersecurity
- Bachelor of Science in Electrical and Computer Engineering
- Bachelor of Science in Computer Science
- Bachelor of Science in Construction Management
- Master of Science in Cybersecurity
- Master of Science in Computer Science
- Master of Science in Engineering Management
- Doctor of Philosophy in Data Science
- Doctor of Philosophy in Computer Science
- Doctor of Philosophy in Technology Management
- Doctor of Philosophy in Cybersecurity
- All Engineering & Technology
- Associate of Arts in General Education
- Bachelor of Arts in Digital Media Design
- Bachelor of Arts in General Studies
- Master of Arts in English
- Master of Arts in Strategic Communication
- Foreign Credential Bridge Program
- All Arts & Humanities
- Graduate Certificate in Forensic and Crime Scene Investigations
- Bachelor of Public Administration
- Bachelor of Science in Homeland Security and Emergency Management
- Minor in Business Law
- Master of Criminal Justice Leadership
- Master of Forensic Sciences
- Master of Science in Homeland Security and Emergency Management
- Doctor of Public Administration
- All Criminal Justice & Public Service
- Paralegal Specialist Certificate Corporations
- Paralegal Specialist Certificate Criminal Law
- Paralegal Specialist Certificate Litigation
- Associate of Science in Paralegal Studies
- Bachelor of Arts in Pre-Law Studies
- Bachelor of Science in Paralegal Studies
- Juris Doctor
- Associate of Science in Human Biology
- Associate of Science in General Education
- Bachelor of Science in Biology
Bachelor of Science in Mathematics
- All Science & Math
- Program Finder
- Undergraduate Admissions
- Graduate Program Admissions
- Military Admissions
- Early College
- Credential & Certificate Programs
- Transfer Information
- Speak to an Advisor
- How to Pay for College
- Financial Aid
- Scholarships
- Tuition & Fees
- NU offers a variety of scholarships to help students reduce their financial burden while focusing on achieving their goals. Explore Scholarships
- Office of the President
- Board of Trustees
- Accreditation
- Course Catalog
- Workforce and Community Education
- Academic Schools/Colleges
- Academies at NU
- NU Foundation
- President’s Circle
- Military & Veterans
- Coast Guard
- Space Force
- National Guard & Reservist
- Military Spouses & Dependents
- Military Resources
- NU proudly serves active duty and Veteran students from all branches of the military — at home, on base, and abroad. Military Admissions
- Online Degrees & Programs
- Consumer Information
- Student Login
- Graduation Events
- Student Portal
- Student Bookstore
- Student Resources
- Dissertation Boot Camp
- Show your NU pride and shop our online store for the latest and greatest NU apparel and accessories! Shop Now
- Request Info
- Our Programs

- Math & Science
Inspiring Minds: The Role of Mathematics in Critical Thinking
Join us for an enlightening conversation with Dr. Igor Subbotin, an esteemed mathematician and educator, as we explore the essential role mathematics plays in our world. Throughout our discussion, we uncover the profound impact that mathematics has on developing critical thinking and problem-solving skills, vital for the 21st-century landscape. Dr. Subbotin, with his extensive background in algebra and passion for the subject, shares his insights on how mathematics serves as both the queen and servant of the sciences, simplifying complex ideas and fostering analytical minds.
Listen in as we delve into the significance of mathematics within the educational sphere, particularly at National University. We emphasize the necessity for inspiring teachers who can ignite a lifelong appreciation for mathematics, crucial in dispelling the common apprehension surrounding the subject. Our journey through the history of algebra reveals its rich tapestry, from ancient civilizations to the Islamic Golden Age, demonstrating the subject's evolution and the collaborative nature of its growth, transcending cultural and geographic divides.
Wrapping up our discussion, Dr. Subbotin shares personal anecdotes from his academic path, influenced by renowned mathematicians like Sergei Chernikov. He highlights the emergence of braces theory, a fascinating new branch of algebra, illustrating the interconnectedness of mathematics and physics. This narrative not only showcases the collaborative spirit within the mathematical community but also reinforces the notion that abstract mathematical theories can significantly influence various scientific fields. Tune in to discover the boundless universe of mathematics, where equations speak the language of nature, and every human activity is interwoven with numerical threads.
- 0:04:04 - The Importance of Mathematics in Science (105 Seconds)
- 0:08:56 - Discovering Mathematics (104 Seconds)
- 0:11:50 - Universal Application of Mathematical Concepts (85 Seconds)
- 0:21:12 - Global Influence of Mathematics (173 Seconds)
- 0:33:38 - Tragic End of Evariste Galois (55 Seconds)
- 0:38:29 - Otto Schmidt (165 Seconds)
- 0:42:52 - The Impact of Group Theory (108 Seconds)
- 0:51:47 - Studying Properties of Young-Baxter Equations (100 Seconds)
- 0:56:16 - Language and Mathematics Similarities and Differences (102 Seconds)
- 1:00:49 - Mathematics and Language Connection (117 Seconds)
Dr. Igor Subbotin
0:00:01 - Announcer
You are listening to the National University Podcast.
0:00:10 - Kimberly King
Hello, I'm Kimberly King. Welcome to the National University Podcast, where we offer a holistic approach to student support, well-being and success- the whole human education. We put passion into practice by offering accessible, achievable higher education to lifelong learners. Today we are talking about the power of mathematics and, according to a recent article in the New York Times, learning mathematics is both crucial to the learning development of the 21st century students. So as not to be imposed upon learners too heavily. So, learning mathematics develops problem-solving skills which combine logic and reasoning in students as they grow.
We're going to be having a great conversation about the power of mathematics coming up on today's show. On today's episode, we're talking about the power of mathematics, and joining us is National University's Dr. Igor Subbotin, and he earned his PhD in mathematics at the Mathematics Institute of the National Academy of Sciences of Ukraine. Before joining National University, he taught mathematics at the most prestigious university in Ukraine, Kiev Polytech Institute. At National University, Dr. Subbotin regularly teaches different mathematics classes and supervises mathematics courses. Dr. Subbotin's main area of research is algebra. His list of publications include more than 170 research articles in algebra published in major mathematics journals around the globe, and he has had the privilege to collaborate with several world-class mathematicians from different countries. He also authored more than 50 articles in mathematics education, dedicated mostly to the theoretical base of some topics of high school and college mathematics, and he's published several books. We welcome you to the podcast, Dr. Subbotin. How are you?
0:02:07 - Igor Subbotin
I'm fine. Thank you very much for inviting me. I'm really happy to be with you, thank you.
0:02:13 - Kimberly King
Thank you. Why don't you fill our audience in a little bit on your mission and your work before we get to today's show topic?
0:02:22 - Igor Subbotin
It's very easy to talk about things that you love it. I love mathematics and felt a love in mathematics a long time ago. I continue loving it, the same kind of, let's say, powers that used to be when I was very young and I love my students and the love to my students even grows. Comparison that I was young, because I got experience and understand people better. I love my university and I have been working for National University for 30 years already and university growth- I looked, I was part of the university development and growth. It was small at that time when I came and now it's a big university with some traditions, prestige, some kind of place in the American higher education and I'm happy to work with this and I'm happy to continue development of the mathematics education in our country, in different countries, and Europe, that I participated in many different collaborations with many different scientists and promote some mathematics- new ideas and also disseminate these ideas, which is extremely important. Thank you for inviting me.
0:03:51 - Kimberly King
Absolutely. I love more than anything, I can hear your passion for teaching and really helping your students understand the joy that you have for mathematics, and so today we're talking about the power of mathematics. And so, Doctor, why is mathematics so useful?
0:04:10 - Igor Subbotin
I will answer for this just bringing the citation from Joseph Louis LaGrange, one of the bright stars on the mathematics horizon. He was born in the middle of the 18th century, I mean, started to work in the middle of the 18th century in Turin, Italy, but he is a French mathematician actually, after all, and he was a key figure in many different mathematics development of that time- special calculus, differential equations. It was a time very in, and he said like that, mathematics as the queen and the servant of all sciences. Mathematics is a queen and the servant.
I know that some other people say that mathematics, that science, became a science only if the science used mathematics. Start to use mathematics, it's number one. And also I would like to repeat the word attributed to Galileo Galilei, who said that mathematics is a language in which God speaks to us. God could be just changed to nature, but the meaning is the same. Our nature, our God, will speak to us through the mathematics language, mathematics language. And why mathematics is so remarkably useful in every single human activity, not only in science, not only in physics, everywhere, everywhere. Number one, philosophically talking about everything. Every single event has some kind of qualities. How can we assess this quality? How we will talk about that?
First of all, we try to measure this in some way- qualitative measurement- also appeals to quantitative measurement. There is no quality without quantity. There is no quantity without quality. There are two structures that inter-influence each other. It's number one. Why mathematics has so much power and why it's so useful? Because the main idea of mathematics is to strip off the second line, details, to look at the stems, not on the leaf and the stems ignoring by some details. When you start to study some physics or chemistry, some kind of events or what happened with them in this specific event, you just miss so many details, so many details- you don't know to what you need to concentrate your attention. In this case, mathematics helps you to strip off of this mail by focusing on the most essential aspects.
Mathematic enables a comprehensive understanding of complex natural processes. It distills vast amounts of information, stripping away irrelevant details to emphasize what truly matters, what truly matters. So mathematics is not a calculation. Mathematics is not only geometry. Mathematics is a way of thinking. This is exactly what we call critical thinking of the highest level of development. That's why mathematics is so powerful. And this mathematics is powerful not only in science. It's powerful in any kind of human activity. And I will tell you what is mathematics' role in this human activity. This is the main thing.
0:08:20 - Kimberly King
Well, I love that you explain mathematics as a language and again your passion comes through. In fact, last time I interviewed you I kept saying, as soon as we were through- I wish you were my mathematics professor, because you share such a passion and you make it easy for others to understand, and that is truly a gift. So thank you. Why is mathematics so universal?
0:08:50 - Igor Subbotin
The idea of universality of mathematics- it belongs to its own structure. What is mathematics study? What is mathematics study? The main process in every single thing, event, and you know, sometime it always amazed me and not only me, maybe, it's amazed many different people for sure, that when some science or some human activity thing face some needs of mathematical analysis, which means qualitative or quantitative analysis, the appropriate corresponding series already exists. You don't have to create something new, it's already there. What does it mean philosophically? For me, it means that this is some kind of answer for the very deep questions that everybody who is doing mathematics asks themselves. What we are doing? Creating new mathematical ideas? Or we are discovering this mathematics world, like a known country? So maybe all this idea exists already and we are just discovering them, like in physics, like in chemistry, like in any other thing, or we are creating these ideas. I believe it's my opinion and not everybody shares this opinion that everything already exists. We are just not inventing, we are exploring these ideas. So what does it mean? So, for example, when we are talking we'll talk today a lot about my favorite area of mathematic- algebra. This is not the same algebra that we are talking about during high school mathematics. No, it's a totally different subject. I will talk about this today.
But the power of algebra based on the idea of isomorphism. Isomorphism, what is that? It means if you have two different structures consisting of two of different subjects, objects of different objects, and you find out some kind of one-to-one relations between these two structures, in which it doesn't matter what you're doing in one subject, in one object, work with the same kind of result for the second object. It's in the isomorphism. You can start to study one area and after that, all the rules that you will come to will work for another way. This is the power of mathematics. Simple examples- you can use the same kind of linear equation to describe many different things, many different things. In mechanic, in accounting, in, let's say, the different disciplines that are directed to the, for example, structural things, some like concrete structures and so on.
It's a very simple example. Idea of isomorphism this is algebraic ideas that just came to our attention, I believe, not so long time ago, maybe 200 years ago, no more. But mathematics, mathematics use it for long period of time, many, many, many years, without understanding what is that. I believe that algebra, which is the most abstract subject in mathematics, could be a wonderful illustration how this idea works. The idea of isomorphism is crucial in explaining how mathematical concepts can be applied across diverse fields. For instance, in algebra, the same equation can be used to solve problem various areas, showcasing the universality of mathematical principles. So we will talk about this today.
0:13:13 - Kimberly King
So interesting- yeah, go ahead.
0:13:16 - Igor Subbotin
Let me add a little bit about your remark about the study of mathematics, how the teacher role is important in that. I would like to assure our future students, or some people, that we have right now at National University, that main idea for selecting faculty for mathematics department for classes, staffing them to the classes, is the idea how these people really feel about the subject, if they're really motivated to bring their knowledge and their passion in the classroom and they really understand with whom they're dealing with. Because it's a very different approach in our study when we come to the class of the elementary teacher future elementary teacher or to some art designers, all of us are very passionate about the subject. All of us understand our role at the university and how to treat students in the right way.
I believe not only me, it's statistical knowledge that most of the hate to mathematics born in the elementary school classrooms, where some teachers hate it and don't understand it enough. That's why our mission, our mission- and we teach elementary teachers also- to bring the light of mathematics understanding to them, to build up the respect to the subject, respect to the teaching. And that's why I believe that major, I would say almost all our students are successful, not because we are not keeping rigor. We are keeping high rigor in our classes, our classes. But we are doing our best not only to fill out students like a job but to light them as a torch in mathematics. Sorry for interruption, but it's an important point that I would like to mention, answering for your remark.
0:15:38 - Kimberly King
I'm glad you did, because it is true that when we're learning, I mean it's almost like now you're playing catch up to get these students to love and have that affair- a love affair- with mathematics and that understanding, and it really does need to start at a younger level, just so that you know we can continue to move forward and grow. So thank you for taking that moment out to explain that, because it really does truly show, and I think we're doing a disservice, you know, for those teachers that are in place and either don't have that love, that understanding, that passion, and then they're, you know, not necessarily bringing up our kids, our children, to love it like you do. So it's good, thank you. Can you discuss abstract algebra and how it's stated and its applications?
0:16:31 - Igor Subbotin
Most of our students who are not math majors, they will not study abstract algebra in the university course. They will just, I believe, will be starting studying, some of them, calculus. Some of them will study just college algebra. Some of them will study linear algebra at most, like computer science people. Abstract algebra, this is only for math majors and this is very interesting to trace the genesis of algebra, how it became totally different from other areas of mathematic language, developed language, develop understanding and what is the most important- at the end I will show this- how this may be one of the most abstract, without any, sometimes, visualization ability, subject became the most useful and most applied. It's interesting. So if I will start about talking about algebra, you immediately just come to the original.
Algebra can be found in the mathematics of ancient civilizations, particularly Babylonian people and ancient Greece, of course, with Euclid, with his famous book Elements. Do you know that the book Elements of Euclid was it's about 2,300 years ago published? by Euclid, and Euclid is a very mystical figure in mathematics because there is not any portrait of Euclid that exists. Most of the mathematician portraits we have it came to us from the anthropology but not Euclid’s picture and according to his, let's say his in quotation input, in mathematics it's too much for one person to be so educated and so powerful. So there is some hypothesis that Euclid this is just, let's say, like nickname for the group of mathematicians of that time they put together their knowledge in the group of elements, elements. It's had in the group of elements. You now that the book elements is the second book by the amount of publications after Bible, only one book that was published more than Euclid. Why? Because during 2000 years, it has been the maybe only textbook for mathematics for our civilization, for 2000 years almost. So, Euclid, ancient Greece, so who started developing equation solving procedure and manipulating symbols to depict mathematical relationships.
After that we jump to the golden age of Islamic, that next significant advancement which was made possible by the writing of academic-like Al-Khwarizmi. Al-Khwarizmi - listen, algorithm. Al-Khwarizmi- [laughs] it’s the same, it's the same. Algorithm come from Al-Khwarizmi name. This is some golden age of the Islamic age, something 15th, 14th, 15th century, when this very famous author wrote the book. I will read the book- “al-Kitāb al-Mukhtaṣar fī Ḥisāb al-Jabr wal-Muqābalah”- translating is going to be the Comprehensive Book on Calculation, Completion and Balancing- Al-Jabr. Al-Jabr, this is a book we named. It was brought to Europe by mathematicians from Middle Eastern countries. So what is interesting? Definitely, this book is not absolutely just created by people from Islamic countries. It was a lot of roots in China, a lot of roots come to India and so on.
Let me remind you my favorite words from brilliant mathematician David Gilbert, who was one of the most prominent, if not most prominent mathematicians in the world in the end of the 19th, beginning of 20th century up to the middle of 20th century. He said that for mathematics, there is no boundary in culture and race. Mathematics considered the entire intellectual world as one country. If you take mathematics, you will not find any other science that would be so internationally developed, internationally developed. And now we have many different countries that work in mathematic development. It was maybe something like 19th century.
The most influential was French mathematics. Before it was Newton, English, England mathematics. At the same time it was German mathematics. After that, again, German mathematics became prevalent. After that, Soviet Union mathematical school became a golden, when it was golden age. It's the most powerful and most developed school.
American mathematics. American mathematics became very, very influential and powerful, but it's mostly after 40 years of the previous century, 20th century, and I will bring you many other examples like that. Every Chinese, Chinese school. Look at China now. How many prominent fields, medal holders and mathematicians we have in China. What a genius was born in India. What a great development.
In my own experience and seeing how the Middle East developed mathematics, about 30, 40 years ago they didn't talk about, for example, abstract algebra. Now they have a few, a few journals in the Middle East, especially in Iranian people. It doesn't matter what kind of relation we have with Iran. Mathematics is unity, it's all people work together and we develop the same subject and we work on the same field, which is extremely important. That's why mathematics is so influential. Why we are doing it? This is the reason, because everybody needs it. Everybody needs it, not only for developing some kind of new technical idea, but also for understanding the world.
So after this Islamic time, symbolic notation was developed by a mathematician during the Renaissance time, European mathematicians during the Renaissance time. What happens at that time? People can solve quadratic equations. Long time ago, linear equation was not a problem at all, but quadratic equation long time ago. But when people face equation of the power 3, power 3 with one variable, it was a big problem. Sooner or later it was solved. Also, what does it mean solving equation? It means to get a formula that will express the solution, the roots of the equation, expressing them through the main algebraic operation addition, subtraction, multiplication, division and so on, and radicals and so on, in one formulas through the coefficient, coefficient- number of this equation, using this equation. So for cube roots it could be huge formula. After that, for four roots, people were successful. They got it.
After they got it, I believe that the creator of this was a mathematician who was nicknamed Tartaglia. Tartaglia mean people with some kind of empire of speaking, Tartaglia in Italy. This, it was a very strange person. He was very- He was not, he didn't have really nice personality, he was, let's say, some kind of gloomy and always not happy guy. But he, according to what I read, he was the person who solved the equation of the power of four. At the same time. Cardano, Federico Cardano, who is a physicist, great physician, great engineer and great mathematician of the time, very big person at the time, star number one in Italy, have heard that Tartaglia has some formula for solving equation of the force power, certain force power.
Why it was so important? At that time, to get position to have some money for doing mathematics was a very difficult thing. It was a very difficult thing. It was very limited opportunity, for example, to be some kind of the mathematician in the court of some kind of prince or king or duke or something like that. So people just applying for this position, they're supposed to go through the competition. Competition looks like that that the persons who would like to apply for the position, two weeks before the meeting, send to each other the list of the problems that they would like that their counterpart solved. A counterpart solved Okay, if you have a formula that nobody knows, you are a winner. It's a big chance that you solve the problems that this person sent to you. But there is no chance that somebody will solve the problem if they don't know the formula. So it was a huge privilege, it was a huge, huge benefit to having the formula. It was a big secret. Nobody knows.
Cardano, who was a huge guy, a huge star at that time, came to this unknown guy, Tartaglia, and asked him tell me please about the formula I have heard you have it. Tell me please. And Tartaglia said okay, but don't tell anybody. For Tartaglia it was a big, big how to say honor to meet a guy like that and he told him the formula. What Cardano did- from the point of view of nowadays, he did a very honest and great thing. He published a book and the end of the book published the appendix and he said this formula was given to me by my esteemed great colleagues Tartaglia. So he didn't try to cheat, he didn't try to get his Tartaglia let's say, copyright, like we said right now. But from point of view of nowadays you can say it was a huge support to the people, to the Tartaglia from the big, big star.
No, guys, that time it was totally different. Tartaglia lost his power to win in competition by publishing this formula. So, change time, change the vision, change the vision. So this time now the formula calls like usually called, usually called something that if you create in mathematics it's always a different person name. Coming to the history, it's Cardano formula, but definitely it was Tertaglia. In mathematics there are some kind of buyer rule that most of the invention in mathematics are called by the name of the people who didn't do this. It's even said like that Bayer rules, okay.
So what happened after that? People started to study the equation of power of five. Next fifth power no success, no success. This way, that way, no success. Nobody can do this, anything. And until October 25, 1811, a brilliant, very unusual, mathematic star was born- Evariste Galois. Evariste Galois, French mathematician. He was born, again, in 1811. He created his main idea and write his main idea in written when he was 16 years old. 16 years old and he was killed when he was 20. Only 70 years after his death, Camille Jordan published his work in his book about matrices, and this is the beginning of modern algebra, beginning of modern algebra.
Do you know what the Evariste Galois finds out? He finds out that any equation, polynomial equation with one variable, with a power greater than four, like five, six, 7, and so on, has no formula at all in general, cannot be found. But partial cases, please. To find some approximate solution, please, but not general. There is no, and never going to happen. It's mathematical power. You see, he proves that it and never going to happen, it's mathematical power. You see, he proves that it's never going to happen that anybody with the hugest star in the world there is no formula in general, case like that. Moreover, he finds out when, in some partial cases, this formula exists and when not. What's the condition for this. This is what. 16 years old how to say, teenager, 16 years old.
He of course tried to find out the opinion of the people who was in power in mathematics that time. He sent his manuscript to Augustin-Louis Cauchy. If you will study calculus- I'm talking to our future audience- you will find Cauchy's name every I mean tens, dozens of times in different theorems and calculus. He was a huge star at that time it was the first quarter maybe, of the 19th century right and he published a lot of different works. He was a genius and he is a genius. And Galois sent him a manuscript and after some time asked what do you think about that? And Augustin-Louis Cauchy said all right to him, I lost it. I don't know if it was true or not. Some people said that after that, the publication of Augustin-Louis Cauchy has some influence on this paper. So it's again, humans are humans everywhere, not only in the economics and history, but also in science, even such straight science like mathematics. Human is human.
So what can we say about this situation? And Evariste Galois continued to promote his idea. He organized special seminars for people who wanted to come there. But he also participated in the revolutionary activity and he was very active in this, and the police decided to say too active, too much active, the police in French, and they sent to him the killer. He just sent him invitation to duel because of some woman. Sorry but it's true and he just came to the duel and before the night of the duel he continued to work on mathematics and he was killed in the duel. It was a main idea. It was political kill, definitely, but he was 20. He was 20 at that time. So you know, teenagers create a new huge area of mathematics.
It started with a name, like Galois theory and we studied Galois theory. But this is a partial idea. The idea was to study, not the numbers, not the equation- operations, operations. This is the power of abstract algebra. This is the power when the abstract algebra was born. Study operation.
I will give you a very simple example that everybody will understand about operations and so on. You know that entire world knows chess game. In different countries we have different names, different names for the checkboard names. We have different names for the figures. We have different names for the different language, for the combinations that we consider. But we have great masters from different countries. They play the same game. They cannot speak common language, but they know the rules and the rules are the same rules. It's operations, how to operate with this special figure in this special situation. This is a rule. So algebra, abstract algebra, they don't deal with the equations, specifically. They don't deal with the numbers. They can deal with the matrices, which are big tables. They can deal with the transformation of the space of the plane, doesn't matter the idea how this object behaves under the operations.
Under the operations.
0:36:20 - Igor Subbotin
It's a huge step. It became a very abstract subject, a very abstract subject and it's very interesting to say the algebra started with the ideals of Galois and the idea of Galois leads us to the group theory. This group, the algebra subject, without operation group is the most possible. Group theory. But group theory was long time stay long time as a group theory of permutations. It's a special object in algebra. Only in 1920s, 1920s, great mathematician, Otto Yulyevich Schmidt. Otto Schmidt, it's a Soviet Union mathematician, Russian but definitely with the German roots. Schmidt, it's German name. Otto Yulyevich Otto, also German name. It's also another kind of brilliant guy and I'm his scientific grandson.
0:37:26 - Kimberly King
Perfect yes.
0:37:30 - Igor Subbotin
Why you will be amazed in a different way. In our department we have biologists, people who study biology. We have now a department called Mathematics and Natural Science. One of these professors is a prominent researcher in biology who uses a lot of statistics, and his dissertation also was supervised by the statistician mathematician statistician, because to study biology you need statistics, you need to watch. Okay, so what is interesting? When we together came four steps back, we will find out that our roots both of us, came to Carl Friedrich Gauss. I am grand-grand-grandson and he is grand-grand-grandson to Carl Friedrich Gauss.
0:38:23 - Kimberly King
Wow, that is fascinating. My goodness Wow.
0:38:27 - Igor Subbotin
The world is unique, it's one. So Otto Yulyevich Schmidt, Otto Schmidt was not only mathematician, with the he, by the way, first wrote the book which called Abstract Group Theory. When this object, in the group object, elements of this set, absolutely abstract, doesn't matter what the nature, only operation is important. Otto Schmitt was the one and is the one of the most famous geodesists about the science of the Earth, and he is well known also as a creator of the first scientific theory how our solar system was born. This is his name. Also, he was a guy who was the, who was the how to say director of the expedition to the North Pole on the ship Chelyuskin, and that time, in 1930s, it was the most like today, let's say, a trip to the moon. It was the same kind of importance for the entire human race. And so, by the way, some of them article in group theory and algebra written in the Chelyuskin during this expedition, written in the Chelyuskin during this expedition and signed up like ships Chelyuskin, whereas it was written Chips Chelyuskin. So he was there in the North Pole and write the book, and write the book and write the article in mathematics, people like that is a brilliant our human civilization topics. Okay. So algebra became very abstract. Nobody expected that algebra became really, really applicable, right. So because I have been working in algebra for some time, I see it in my own eye when the group theory subject just transformed to the new abstract algebra. Of course I was not born in 1920s when it came, but in 1970s I see the most peak of development on the infinite group theory, and now I see that some other subject was developed like that. Let me continue with the history and I will tell you a very exciting thing about how algebra, so abstract, became so useful and became so applicable.
Next step was German mathematicians, like we are supposed to mention David Hilbert and his school, and also the biggest star in mathematics for all times, Emmy Noether. Emmy Noether, this is not only you know, of course. Everybody knows about Sofia Kovalevskaya. Sofia Kovalevskaya or Gepardia Alexandriyevskaya, some other woman who brings their huge input in mathematics, but Emmy Noether is number one. She was a German mathematician. In 1938, she immigrated, like many other people, from Nazi Germany to the United States and I believe she was a professor in Bryn Maur College after her death. She developed the main idea of investigating some algebraic structure like rings, fields, groups and so on, the idea of chains. I'm not going to proceed with this too far, but she gave us the instruments, the tools to open these fields of investigation. Everybody up to now work on that, everybody up to now work on this and will continue, because this is only one, let's say by now, useful tool to study infinite structure, algebraic structures. So it's very important to mention that again.
That algebra abstract algebra, I would like to underline this was created by many different people but having their definitely first step and the most important input by the genius Evariste Galois and in particular, group theory, has made great progress in the sphere of new ideas and theorems. Many different mathematicians brought their attention and now this is a very well-developed part of algebra that have their application in physics, in cosmology, in painting, in art, in crystallography, everywhere where we have symmetry, symmetry. You know everybody what now? What's the tool to study symmetry, group theory. So it was created for solving equations, but find their application in any science that dealing with the symmetry, any kind of symmetry, geometrical symmetry or some other kind of symmetry, elementary particle symmetry, cosmology, and so on and so on. But I would like to finish with the development of how it was developed and I'm ready for your next question because I will continue this forever, definitely.
0:44:26 - Kimberly King
It's really fascinating, though, to hear the history and to hear all of the countries that have been involved with the very beginning, the establishment and the beginning of mathematics. So this is quite fascinating. We do have to take a quick break, doctor, if you don't mind, and we'll be right back with you in just a moment. Don't go away and hold onto those thoughts, stay with us. You Thank you. And now back to our interview with National University's math professor, Dr. Igor Subbotin, and we're discussing the power of mathematics and, doctor, this has been so interesting, just hearing the history of it and how it is all the nations working together, as we were just discussing, without a particular agenda other than the love of mathematics. The answers, we say numbers don't lie, and so, with everybody working together, it is universal. Can you talk about the bridge between high abstraction and realm?
0:46:14 - Igor Subbotin
I would be happy to do it. I will give you some kind of examples that I faced myself lately.
Okay, this is again for our future students. It's very important that the people who will teach you the subject be active in this subject, be professional in this subject, not just read the book and explain book to you, but do something by their hands in order to develop and to bring very modest input, but input in the object. I will give you some interesting story about that that based on my own experience lately, I have a very old friend not old person, old friend to me which we are friends, we have our friendship, for you cannot believe more than 50 years and we keep our collaboration, maybe the same amount of years because we are from the same school. Our supervisor was a brilliant star who was one of the founders of Infinite Group Theory, Sergei Chernikov. He is a huge international star and we are proud to be his students. I was lucky to work under his supervision and in his seminar since 1967 to 1987 when he passed away. I was lucky and my friends that I'm talking about, I can give you his name. Somebody can go to Google to look and find out who is it. It's Leonid Kurdachenko. It's Ukrainian mathematician, very, very, very famous mathematician in our area, abstract algebra, distinguished professor, and so on and so on and my close friends. We worked together for many years and we both have our roots in working in abstract algebra, in group theory, and we've been witnesses and we are witnesses about the time when the group theory and pheningo theory was very powerful in new development field and so on. But lately we found out, by some different reasons, some people came to work in so-called braces theory. Braces, not the stomatological braces, not the braces that you use like parentheses, some kind of parentheses. Algebra brace is totally different. It's algebraic structure, new algebraic structure. What is it about? Taking example from physical algebraic equation, we have behavior of particles and waves which make possible to predict what will happen next, to explain nature of phenomena. Again, this is about symmetry, for example, biological sign, complete genetic interaction, dynamics and so on. Algebra is resonant also to artistic work, but lately it's happened like that. Let me give you the exact what I would like to say. The theory of braces, the theory of braces is very young, very young, it's just right now.
It has its roots in addressing the Young-Baxter equation, a fundamental concept with profound amplification in both pure mathematics and physics. It originated from the groundbreaking work of the Nobel Prize winner, physicist Young, of the Nobel Prize winner, physicist Young, in the realm of statistical mechanics and, independently, in the contribution of Baxter to the 8-vertex model. It came from the knot theory and came from the statistical mechanics, its quantum theory. This theory holds substantial significance across diverse domains such as knot theory, braid theory, operator theory, hoppe, algebra, quantum groups, Tremont Foyle and monodromy of the differential equation. This is a fundamental equation in mathematics and physics that arises in the study of central algebraic structure, arises the study of central algebraic structure and it came to our attention thanks to the works in some first time in 1960s. But about the theory itself is thanks to the work of other mathematician, is became popular since 2008,9.
Many people just came to study this because it has huge application. What is it about? It's about to find the properties of the solution of this equation. Solution of this equation is not numbers, it's matrices. It's matrices, different kinds of matrices, special subjects in algebra. We don't have a general formula or a general approach to solving this equation. We don't have it, but it's very important to us not waiting until maybe we'll never have it, who knows?
I gave you today an example of a various Galois equation. There is no formula for the solution of the fifth power equation. There is no formula. We are doing this approximately. We have many methods to solve approximately, which is enough for us. For the Young-Baxter equation. We have some situation, but study the properties of solutions as very, very important for many different disciplines and the people start to study this kind of equation, study the properties of this equation, even though we don't have these solutions. We don't have solutions, but we study properties of the solution and they find out that this just could be studied with the approach of abstract algebra. The properties of this solution could be described with the help of the new algebraic structure, old algebraic structure groups, fields, rings and so on. It's classical structures already. This is absolutely young, absolutely young and new. This is braces. Braces like a fusion of two groups together. It's very difficult to describe on the fingers but it's very important.
Solution of the Young-Baxter equation, known as the Young-Baxter matrices or R matrices, have found numerous applications beyond their original context. People start to study this. My friend, Leonid Kordachenko, just tried to apply the ideas that we had developed in the group theory, not we. Saying we, I mean all mathematics community, not myself, separate, okay. And he was so kind, he involved me to this and we together started to work on some specific points of it me to this and we together start to work on some specific points of it and find out that, you know, the idea of group theory works there. Works there, not different results different, the same approach, the same approach, the same idea how to mine this, but totally different results. Totally different results. But its results are natural and ideas natural. So we start to work on this and let's say we work with success and we are doing this for the last two years and we published already a few articles about that and we also developed some and delivered some talks in different conferences and was very welcome in the community of the people who work in this area and very famous and algebraic for there. Why? Because of applications.
But what is interesting, even though this is absolutely new structure in algebra, not like we used to study and we will study in our algebra course in our university- New structure, absolutely new. The approaches that we use, the approaches work there in the same way. So the ideas work there. So what I would like to say- It exists. When physicists need it, mathematicians said welcome, we have it. We have it. We were just a little bit adjusted and the lock will be open. It's the power of mathematics. That's why we need to study that. That's why everybody likes to study mathematics around the globe. That's why there's no difference to us, to our colleagues, whoever, wherever they live, whether it's race, whether it's nationality, whether it's language, we don't care. We are one community. We united the globe, we united the human nation together like nobody else.
0:56:03 - Kimberly King
Well, I love that and I wish that we can continue to just be united as a nation and not get politics involved in everything. Mathematics, there is a universal answer and that's just beautiful. And speaking of the language, how are language and mathematics alike and what are the differences? I know you've been talking a little bit about this, but I just I really do love that you've talked about the history of it in a universal manner, but talk about the reasons why mathematics and language are alike and different.
0:56:36 - Igor Subbotin
Mathematics and language. You know, English is not my native language, as you may have already seen, and my third language that I use, and analyzing my experience in writing mathematics and analyzing my experience in writing mathematics in Russian, in Ukrainian, in English, I can find out some very interesting things of the cross influence of the language and mathematics. As I told you before, mathematics is a language, Mathematics is a language. So, in my my opinion, it looks like that we have a box which called mathematics. On the input, we have a regular language. We translate this language in mathematics language using symbols, place this in the box and forget about everything. Forget about the, what we are dealing with. We are just using the rules automatically, like in algebra, solving equation. We don't care what the A, what the B, what the C. We have a formula. We substitute number to the formula, get the result, go back, output and translate the solution to the common language. This is how it works, right In reality. But it's very interesting that English, in my opinion.
I am not a polyglot. I don't have too many languages in my, let's say, possession, but I'm really good at Russian and I'm not bad at Ukrainian. I can express myself in English, but English is a very interesting language. It's totally different than the language that I started to use before. English is a beautiful language because it's close to mathematics nature. It's a very straightforward language. Everything is structural. For example, a Russian can say something like this is a beautiful girl and this girl is beautiful. I can say beautiful, this girl in Russian. It will be the same meaning In English. No, in the order in the sentence. It's very, very important. So it became English, close to mathematics.
Also, I find out when I translate my articles. For example, I need to write an abstract. For some international journal, it's going to be in two languages, for example Russian and English. I look in English. I have, let's say, 75% of the amount of sentences written in Russian words. It's shorter, straightforward. Also, in English we prefer something like short sentences. In Russia, for example, in Leo Tolstoy, War and Peace, you will find War and Peace. You will find something like two pages languages by the same Charles Dickens. I found out that the same in Charles Dickens' writing huge sentences. But for mathematics, English- English maybe the most, in my experience, the most close to express their idea, knowledge, very easy to understand, very easy to write, mathematics, much easier to write in any other languages, it's number one. So language and mathematics, while seemingly distant, share common futures and serve as conveyors of thoughts, ideas and concepts.
Symbolic system, use words and structure to represent ideas, allowing for the exchange of information without requiring a deep understanding of the subject matter, which never happened in mathematics. Language, much more rich structure. You can explain something that you don't understand for yourself. For example, I talked today about Young-Baxter equation. I don't want to pretend that I understand this equation absolutely clearly like physicists no way. I look at this from one part, from the algebraic approach, and also I'm not far to be a full understanding of this. Okay, but I can express my opinion about, I can express my opinion about, I can express my approach and so on.
It's a language, mathematics. You cannot do it. It's only one subject that always answers for the question why, why? And this is very important. That's why I love mathematics. But definitely language and mathematics have a lot in common, because there is no mathematics without language and I believe that we cannot express any of our thoughts without language. Mathematics is a kind of shortness and compact. It's some kind of observations that they make, that when you have an information, some piece of information and you just really study this. It became very small in your brain and take only one small cell. When you need to go back, you just open it up again in the big structure. Mathematics does the same in language so-called word problems. It's interesting.
1:02:13 - Kimberly King
It is so interesting also the way you have explained that English has mathematical you know, and when you compare it to Russian or Ukrainian, I mean I can't even imagine. I have heard that English is one of the hardest languages to speak and to learn, which I don't believe. That, because I think Russian would be just off the top. I can't even imagine. So kudos to you for being so proficient and putting this all together. I think it's so fascinating and I love interviewing you every time we have you on. So thank you for your time today. This has been wonderful that you've shared your knowledge today. This has been wonderful that you've shared your knowledge, and if you want more information, you can visit National University's website. It's nu.edu. Thank you, doctor, so very much for your time.
1:03:01 - Igor Subbotin
Thank you, Kimberly. I really appreciate it. I'm always happy to meet with you and I was happy to work with you as a one team to promote my favorite subject mathematics.
1:03:15 - Kimberly King
We need mathematicians. Thank you so much.
1:03:17 - Igor Subbotin
Thank you, thank you.
1:03:22 - Kimberly King
You've been listening to the National University Podcast. For updates on future or past guests, visit us at nu.edu. You can also follow us on social media. Thanks for listening.
Show Quotables
Search the site
Modal window with site-search and helpful links
Featured Programs
- Business and Management
- Computer Science
- Teaching and Credentials
Helpful Links
- Admissions & Application Information
- Online College Degrees & Programs
- Student Services
- Request Your Transcripts
Terms & Conditions
By submitting your information to National University as my electronic signature and submitting this form by clicking the Request Info button above, I provide my express written consent to representatives of National University and National University affiliates (including City University of Seattle) to contact me about educational opportunities. This includes the use of automated technology, such as an automatic dialing system and pre-recorded or artificial voice messages, text messages, and mail, both electronic and physical, to the phone numbers (including cellular) and e-mail address(es) I have provided. I confirm that the information provided on this form is accurate and complete. I also understand that certain degree programs may not be available in all states. Message and data rates may apply. Message frequency may vary.
I understand that consent is not a condition to purchase any goods, services or property, and that I may withdraw my consent at any time by sending an email to [email protected] . I understand that if I am submitting my personal data from outside of the United States, I am consenting to the transfer of my personal data to, and its storage in, the United States, and I understand that my personal data will be subject to processing in accordance with U.S. laws, unless stated otherwise in our privacy policy . Please review our privacy policy for more details or contact us at [email protected] .
By submitting my information, I acknowledge that I have read and reviewed the Accessibility Statement .
By submitting my information, I acknowledge that I have read and reviewed the Student Code of Conduct located in the Catalog .
National University
Chat Options
- Share full article
Advertisement
Supported by
Gray Matter
Does Math Make You Smarter?

By Manil Suri
Dr. Suri is a professor of mathematics at the University of Maryland, Baltimore County.
- April 13, 2018

Does studying mathematics enhance your overall mental prowess?
Abraham Lincoln certainly believed so, embarking on the arduous task of mastering Euclid’s treatises on geometry to increase his cognitive capacities, in particular his linguistic and logical abilities. This idea — that mathematics strengthens your mind much as physical exercise strengthens your body, helping you negotiate a variety of mental challenges — goes all the way back to Plato. Alive and well in today’s world, it is one reason popularly given for why everyone should study mathematics.
So it can come as a surprise to learn that cognitive psychologists have a different take on the issue. Various studies point to the conclusion that subjecting the mind to formal discipline — as when studying geometry or Latin — does not, in general, engender a broad transfer of learning. There is no sweeping increase of a general capacity for tasks like writing a speech or balancing a checkbook.
But surely a narrower claim is true: that mathematics, so systematically built as it is on inference, must develop logical thinking. Right?
By “logical,” I mean the kind of thinking needed to solve the following problem:
Four cards are laid in front of you, each of which, it is explained, has a letter on one side and a number on the other. The sides that you see read E, 2, 5 and F. Your task is to turn over only those cards that could decisively prove the truth or falsity of the following rule: “If there is an E on one side, the number on the other side must be a 5.” Which ones do you turn over?
Clearly, the E should be turned over, since if the other side is not a 5, the rule is untrue. And the only other card that should be flipped is the 2, since an E on the other side would again disprove the rule. Turning over the 5 or the F doesn’t help, since anything on the other side would be consistent with the rule — but not prove it to be true.
[ ALSO READ: Standing Up at Your Desk Could Make You Smarter ]
This innocuous-looking puzzle, a variation of which was introduced by the British psychologist Peter Wason in 1966, has been called “the single most investigated paradigm in the psychology of reasoning.” If you answered E and 2, congratulations: You are among the roughly 10 percent of the public able to solve the puzzle. Many reasons have been advanced for this poor showing, including the lack of relevance of such an abstract exercise to people’s daily lives.
We are having trouble retrieving the article content.
Please enable JavaScript in your browser settings.
Thank you for your patience while we verify access. If you are in Reader mode please exit and log into your Times account, or subscribe for all of The Times.
Thank you for your patience while we verify access.
Already a subscriber? Log in .
Want all of The Times? Subscribe .
- Our Mission
5 Ways to Stop Thinking for Your Students
Too often math students lean on teachers to think for them, but there are some simple ways to guide them to think for themselves.

Who is doing the thinking in your classroom? If you asked me that question a few years ago, I would have replied, “My kids are doing the thinking, of course!” But I was wrong. As I reflect back to my teaching style before I read Building Thinking Classrooms by Peter Liljedahl (an era in my career I like to call “pre-thinking classroom”), I now see that I was encouraging my students to mimic rather than think .
My lessons followed a formula that I knew from my own school experience as a student and what I had learned in college as a pre-service teacher. It looked like this: Students faced me stationed at the board; I demonstrated a few problems while students copied what I wrote in their notes. I would throw out a few questions to the class to assess understanding. If a few kids answered correctly, I felt confident that the lesson had gone well. Some educators might call this “ I do, we do, you do .”
What’s wrong with this formula? When it was time for them to work independently, which usually meant a homework assignment because I used most of class time for direct instruction, the students would come back to class and say, “The homework was so hard. I don’t get it. Can you go over questions 1–20?” Exhausted and frustrated, I would wonder, “But I taught it—why didn’t they get it?”
Now in the “peri-thinking classroom” era of my career, my students are often working at the whiteboards in random groups as outlined in Liljedahl’s book. The pendulum has shifted from the teacher doing the thinking to the students doing the thinking. Do they still say, “I don’t get it!”? Yes, of course! But I use the following strategies to put the thinking back onto them.
5 Ways to Get Your Students to Think
1. Answer questions with a refocus on the students’ point of view. Liljedahl found in his research that students ask three types of questions: “(1) proximity questions—asked when the teacher is close; (2) stop thinking questions—most often of the form ‘is this right’ or ‘will this be on the test’; and (3) keep thinking questions—questions that students ask so they can get back to work.” He suggests that teachers acknowledge “proximity” and “stop thinking questions” but not answer them.
Try these responses to questions that students ask to keep working:
- “What have you done so far?”
- “Where did you get that number?”
- “What information is given in the problem?”
- “Does that number seem reasonable in this situation?”
2. Don’t carry a pencil or marker. This is a hard rule to follow; however, if you hold the writing utensil, you’ll be tempted to write for them . Use verbal nudges and hints, but avoid writing out an explanation. If you need to refer to a visual, find a group that has worked out the problem, and point out their steps. Hearing and viewing other students’ work is more powerful .
3. We instead of I . When I assign a handful of problems for groups to work on at the whiteboards, they are tempted to divvy up the task. “You do #30, and I’ll do #31.” This becomes an issue when they get stuck. I inevitably hear, “Can you help me with #30? I forgot how to start.”
I now require questions to use “we” instead of “I.” This works wonders. As soon as they start to ask a question with “I,” they pause and ask their group mates. Then they can legitimately say, “ We tried #30, and we are stumped.” But, in reality, once they loop in their group mates, the struggling student becomes unstuck, and everyone in the group has to engage with the problem.
4. Stall your answer. If I hear a basic computation question such as, “What is 3 divided by 5?” I act like I am busy helping another student: “Hold on, I need to help Marisela. I’ll be right back.” By the time I return to them, they are way past their question. They will ask a classmate, work it out, or look it up. If the teacher is not available to think for them, they learn to find alternative resources.
5. Set boundaries. As mentioned before, students ask “proximity” questions because I am close to them. I might reply with “Are you asking me a thinking question? I’m glad to give you a hint or nudge, but I cannot take away your opportunity to think.” This type of response acknowledges that you are there to help them but not to do their thinking for them.
When you set boundaries of what questions will be answered, the students begin to more carefully craft their questions. At this point of the year, I am starting to hear questions such as, “We have tried solving this system by substitution, but we are getting an unreasonable solution. Can you look at our steps?” Yes!
Shifting the focus to students doing the thinking not only enhances their learning but can also have the effect of less frustration and fatigue for the teacher. As the class becomes student-centered, the teacher role shifts to guide or facilitator and away from “sage on the stage.”
As another added benefit, when you serve as guide or facilitator, the students are getting differentiated instruction and assessment. Maybe only a few students need assistance with adding fractions, while a few students need assistance on an entirely different concept. At first, you might feel like your head is spinning trying to address so many different requests; however, as you carefully sift through the types of questions you hear, you will soon be comfortable only answering the “keep thinking” questions.
Engaging Maths
Dr catherine attard, promoting creative and critical thinking in mathematics and numeracy.
- by cattard2017
- Posted on June 25, 2017
What is critical and creative thinking, and why is it so important in mathematics and numeracy education?
Numeracy is often defined as the ability to apply mathematics in the context of day to day life. However, the term ‘critical numeracy’ implies much more. One of the most basic reasons for learning mathematics is to be able to apply mathematical skills and knowledge to solve both simple and complex problems, and, more than just allowing us to navigate our lives through a mathematical lens, being numerate allows us to make our world a better place.
The mathematics curriculum in Australia provides teachers with the perfect opportunity to teach mathematics through critical and creative thinking. In fact, it’s mandated. Consider the core processes of the curriculum. The Australian Curriculum (ACARA, 2017), requires teachers to address four proficiencies : Problem Solving, Reasoning, Fluency, and Understanding. Problem solving and reasoning require critical and creative thinking (). This requirement is emphasised more heavily in New South wales, through the graphical representation of the mathematics syllabus content , which strategically places Working Mathematically (the proficiencies in NSW) and problem solving, at its core. Alongside the mathematics curriculum, we also have the General Capabilities , one of which is Critical and Creative Thinking – there’s no excuse!
Critical and creative thinking need to be embedded in every mathematics lesson . Why? When we embed critical and creative thinking, we transform learning from disjointed, memorisation of facts, to sense-making mathematics. Learning becomes more meaningful and purposeful for students.
How and when do we embed critical and creative thinking?
There are many tools and many methods of promoting thinking. Using a range of problem solving activities is a good place to start, but you might want to also use some shorter activities and some extended activities. Open-ended tasks are easy to implement, allow all learners the opportunity to achieve success, and allow for critical thinking and creativity. Tools such as Bloom’s Taxonomy and Thinkers Keys are also very worthwhile tasks. For good mathematical problems go to the nrich website . For more extended mathematical investigations and a wonderful array of rich tasks, my favourite resource is Maths300 (this is subscription based, but well worth the money). All of the above activities can be used in class and/or for homework, as lesson starters or within the body of a lesson.
Will critical and creative thinking take time away from teaching basic concepts?
No, we need to teach mathematics in a way that has meaning and relevance, rather than through isolated topics. Therefore, teaching through problem-solving rather than for problem-solving. A classroom that promotes and critical and creative thinking provides opportunities for:
- higher-level thinking within authentic and meaningful contexts;
- complex problem solving;
- open-ended responses; and
- substantive dialogue and interaction.
Who should be engaging in critical and creative thinking?
Is it just for students? No! There are lots of reasons that teachers should be engaged with critical and creative thinking. First, it’s important that we model this type of thinking for our students. Often students see mathematics as black or white, right or wrong. They need to learn to question, to be critical, and to be creative. They need to feel they have permission to engage in exploration and investigation. They need to move from consumers to producers of mathematics.
Secondly, teachers need to think critically and creatively about their practice as teachers of mathematics. We need to be reflective practitioners who constantly evaluate our work, questioning curriculum and practice, including assessment, student grouping, the use of technology, and our beliefs of how children best learn mathematics.
Critical and creative thinking is something we cannot ignore if we want our students to be prepared for a workforce and world that is constantly changing. Not only does it equip then for the future, it promotes higher levels of student engagement, and makes mathematics more relevant and meaningful.
How will you and your students engage in critical and creative thinking?
Share this:
- Pingback: Critical Thinking, Mathematics, and McDonald’s | Engaging Maths
- Pingback: Beach Towels and Pencil Cases: Interesting, Inquiry-based Mathematical Investigations | Engaging Maths
Leave a comment Cancel reply
- Already have a WordPress.com account? Log in now.
- Subscribe Subscribed
- Copy shortlink
- Report this content
- View post in Reader
- Manage subscriptions
- Collapse this bar
Click through the PLOS taxonomy to find articles in your field.
For more information about PLOS Subject Areas, click here .
Loading metrics
Open Access
Peer-reviewed
Research Article
Does mathematics training lead to better logical thinking and reasoning? A cross-sectional assessment from students to professors
Roles Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Project administration, Resources, Writing – original draft, Writing – review & editing
Affiliation School of Mathematics and Statistics, The University of Sydney, Sydney, Australia
Roles Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Writing – original draft, Writing – review & editing
* E-mail: [email protected]
Affiliation School of Arts and Humanities, Edith Cowan University, Joondalup, Australia
- Clio Cresswell,
- Craig P. Speelman

- Published: July 29, 2020
- https://doi.org/10.1371/journal.pone.0236153
- Peer Review
- Reader Comments
Mathematics is often promoted as endowing those who study it with transferable skills such as an ability to think logically and critically or to have improved investigative skills, resourcefulness and creativity in problem solving. However, there is scant evidence to back up such claims. This project tested participants with increasing levels of mathematics training on 11 well-studied rational and logical reasoning tasks aggregated from various psychological studies. These tasks, that included the Cognitive Reflection Test and the Wason Selection Task, are of particular interest as they have typically and reliably eluded participants in all studies, and results have been uncorrelated with general intelligence, education levels and other demographic information. The results in this study revealed that in general the greater the mathematics training of the participant, the more tasks were completed correctly, and that performance on some tasks was also associated with performance on others not traditionally associated. A ceiling effect also emerged. The work is deconstructed from the viewpoint of adding to the platform from which to approach the greater, and more scientifically elusive, question: are any skills associated with mathematics training innate or do they arise from skills transfer?
Citation: Cresswell C, Speelman CP (2020) Does mathematics training lead to better logical thinking and reasoning? A cross-sectional assessment from students to professors. PLoS ONE 15(7): e0236153. https://doi.org/10.1371/journal.pone.0236153
Editor: Jérôme Prado, French National Center for Scientific Research (CNRS) & University of Lyon, FRANCE
Received: January 13, 2020; Accepted: June 30, 2020; Published: July 29, 2020
Copyright: © 2020 Cresswell, Speelman. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Data Availability: All relevant data are within the paper and its Supporting Information files.
Funding: The authors received no specific funding for this work.
Competing interests: The authors have declared that no competing interests exist.
Introduction
Mathematics is often promoted as endowing those who study it with a number of broad thinking skills such as: an ability to think logically, analytically, critically and abstractly; having capacity to weigh evidence with impartiality. This is a view of mathematics as providing transferable skills which can be found across educational institutions, governments and corporations worldwide. A view material to the place of mathematics in curricula.
Consider the UK government’s commissioned inquiry into mathematics education “Making Mathematics Count” ascertaining the justification that “mathematical training disciplines the mind, develops logical and critical reasoning, and develops analytical and problem-solving skills to a high degree” [ 1 p11]. The Australian Mathematical Sciences Institute very broadly states in its policy document “Vision for a Maths Nation” that “Not only is mathematics the enabling discipline, it has a vital productive role planning and protecting our well-being” (emphasis in original) [ 2 ]. In Canada, British Columbia’s New 2016 curriculum K-9 expressly mentions as part of its “Goals and Rationale”: “The Mathematics program of study is designed to develop deep mathematical understanding and fluency, logical reasoning, analytical thought, and creative thinking.” [ 3 ]. Universities, too, often make such specific claims with respect to their teaching programs. “Mathematics and statistics will help you to think logically and clearly, and apply a range of problem-solving strategies” is claimed by The School of Mathematical Sciences at Monash University, Australia [ 4 ]. The School of Mathematics and Statistics at The University of Sydney, Australia, directly attributes as part of particular course objectives and outcomes skills that include “enhance your problem-solving skills” as part of studies in first year [ 5 ], “develop logical thinking” as part of studies in second year, which was a statement drafted by the lead author in fact [ 6 ], and “be fluent in analysing and constructing logical arguments” as part of studies in third year [ 7 ]. The University of Cambridge’s Faculty of Mathematics, UK, provides a dedicated document “Transferable Skills in the Mathematical Tripos” as part of its undergraduate mathematics course information, which again lists “analytic ability; creativity; initiative; logical and methodical reasoning; persistence” [ 8 ].
In contrast, psychological research, which has been empirically investigating the concept of transferability of skills since the early 1900s, points quite oppositely to reasoning skills as being highly domain specific [ 9 ]. Therefore, support for claims that studying mathematics engenders more than specific mathematics knowledge is highly pertinent. And yet it is largely absent. The 2014 Centre for Curriculum Redesign (CCR) four part paper “Mathematics for the 21st Century: What Should Students Learn?” concludes in its fourth paper titled “Does mathematics education enhance higher-order thinking skills?” with a call to action “… there is not sufficient evidence to conclude that mathematics enhances higher order cognitive functions. The CCR calls for a much stronger cognitive psychology and neuroscience research base to be developed on the effects of studying mathematics” [ 10 ].
Inglis and Simpson [ 11 ], bringing up this very issue, examined the ability of first-year undergraduate students from a high-ranking UK university mathematics department, on the “Four Cards Problem” thinking task, also known as the Wason Selection Task. It is stated as follows.
Each of the following cards have a letter on one side and a number on the other.
Here is a rule: “if a card has a D on one side, then it has a 3 on the other”. Your task is to select all those cards, but only those cards, which you would have to turn over in order to find out whether the rule is true or false. Which cards would you select?
This task involves understanding conditional inference, namely understanding the rule “If P then Q” and with this, deducing the answer as “P and not Q” or “D and 7”. Such logical deduction indeed presents as a good candidate to test for a potential ability of the mathematically trained. This task has also been substantially investigated in the domain of the psychology of reasoning [ 12 p8] revealing across a wide range of publications that only around 10% of the general population reach the correct result. The predominant mistake being to pick “D and 3”; where in the original study by Wason [ 13 ] it is suggested that this was picked by 65% of people. This poor success rate along with a standard mistake has fuelled interest in the task as well as attempts to understand why it occurs. A prevailing theory being the so named matching bias effect; the effect of disproportionately concentrating on items specifically mentioned in the situation, as opposed to reasoning according to logical rules.
Inglis and Simpson’s results isolated mathematically trained individuals with respect to this task. The participants were under time constraint and 13% of the first-year undergraduate mathematics students sampled reached the correct response, compared to 4% of the non-mathematics (arts) students that was included. Of note also was the 24% of mathematics students as opposed to 45% of the non-mathematics students who chose the standard mistake. The study indeed unveiled that mathematically trained individuals were significantly less affected by the matching bias effect with this problem than the individuals without mathematics training. However, the achievement of the mathematically trained group was still far from masterful and the preponderance for a non-standard mistake compared with non-mathematically trained people is suggestive. Mathematical training appears to engender a different thinking style, but it remains unclear what the difference is.
Inglis, Simpson and colleagues proceeded to follow up their results with a number of studies concentrated on conditional inference in general [ 14 , 15 ]. A justification for this single investigatory pathway being that if transfer of knowledge is present, something subtle to test for in the first place, a key consideration should be the generalisation of learning rather than the application of skills learned in one context to another (where experimenter bias in the choice of contexts is more likely to be an issue). For this they typically used sixteen “if P then Q” comprehension tasks, where their samples across a number of studies have included 16-year-old pre-university mathematics students (from England and Cyprus), mathematics honours students in their first year of undergraduate university study, third year university mathematics students, and associated control groups. The studies have encompassed controls for general intelligence and thinking disposition prior to training, as well as follows ups of up to two years to address the issue of causation. The conclusive thinking pattern that has emerged is a tendency of the mathematical groups towards a greater likelihood of rejecting the invalid denial of the antecedent and affirmation of the consequent inferences. But with this, and this was validated by a second separate study, the English mathematics group actually became less likely to endorse the valid modus tollens inference. So again, mathematical training appears to engender a different thinking style, but there are subtleties and it remains unclear what the exact difference is.
This project was designed to broaden the search on the notion that mathematics training leads to increased reasoning skills. We focused on a range of reasoning problems considered in psychological research to be particularly insightful into decision making, critical thinking and logical deduction, with their distinction in that the general population generally struggles with answering them correctly. An Australian sample adds diversity to the current enquiries that have been European focussed. Furthermore, in an effort to identify the impact of mathematics training through a possible gradation effect, different levels of mathematically trained individuals were tested for performance.
Well-studied thinking tasks from a variety of psychological studies were chosen. Their descriptions, associated success rates and other pertinent details follows. They were all chosen as the correct answer is typically eluded for a standard mistake.
The three-item Cognitive Reflection Test (CRT) was used as introduced by Frederick [ 16 ]. This test was devised in line with the theory that there are two general types of cognitive activity: one that operates quickly and without reflection, and another that requires not only conscious thought and effort, but also an ability to reflect on one’s own cognition by including a step of suppression of the first to reach it. The three items in the test involve an incorrect “gut” response and further cognitive skill is deemed required to reach the correct answer (although see [ 17 ] for evidence that correct responses can result from “intuition”, which could be related to intelligence [ 18 ]).
In a lake, there is a patch of lily pads. Every day, the patch doubles in size. If it takes 48 days for the patch to cover the entire lake, how long would it take for the patch to cover half of the lake?
If it takes 5 machines 5 minutes to make 5 widgets, how long would it take 100 machines to make 100 widgets?
Bat and ball
A bat and a ball cost $1.10 in total. The bat costs a dollar more than the ball. How much does the ball cost?
The solutions are: 47 days for the Lily Pads problem, 5 minutes for the Widgets problem and 5 cents for the Bat and Ball problem. The considered intuitive, but wrong, answers are 24 days, 100 minutes and 10 cents, respectively. These wrong answers are attributed to participants becoming over focused on the numbers so as to ignore the exponential growth pattern in the Lily Pads problem, merely complete a pattern in numbers in the Widgets problem, and neglect the relationship “more than” in the Bat and Ball problem [ 19 ]. The original study by Frederick [ 16 ] provides a composite measure of the performance on these three items, with only 17% of those studied (n = 3428) reaching the perfect score. The CRT has since been studied extensively [ 19 – 21 ]. Research using the CRT tends not to report performance on the individual items of the test, but rather a composite measure of performance. Attridge and Inglis [ 22 ] used the CRT as a test for thinking disposition of mathematics students as one way to attempt to disentangle the issue of filtering according to prior thinking styles rather than transference of knowledge in successful problem solving. They repeat tested 16-year old pre-university mathematics students and English literature students without mathematics subjects at a one-year interval and found no difference between groups.
Three problems were included that test the ability to reason about probability. All three problems were originally discussed by Kahneman and Tversky [ 23 ], with the typically poor performance on these problems explained by participants relying not on probability knowledge, but a short-cut method of thinking known as the representativeness heuristic. In the late 1980s, Richard Nisbett and colleagues showed that graduate level training in statistics, while not revealing any improvement in logical reasoning, did correlate with higher-quality statistical answers [ 24 ]. Their studies lead in particular to the conclusion that comprehension of, what is known as the law of large numbers, did show improvement with training. The first of our next three problems targeted this law directly.
- (a). the larger hospital
- (b). the smaller hospital
- (c). about the same (that is, within 5 percent of each other)
Kahneman and Tversky [ 23 ] reported that, of 50 participants, 12 chose (a), 10 chose (b), and 28 chose (c). The correct answer is (b), for the reason that small samples are more likely to exhibit extreme events than large samples from the same population. The larger the sample, the more likely it will exhibit characteristics of the parent population, such as the proportion of boys to girls. However, people tend to discount or be unaware of this feature of sampling statistics, which Kahneman and Tversky refer to as the law of large numbers. Instead, according to Kahneman and Tversky, people tend to adhere to a fallacious law of small numbers, where even small samples are expected to exhibit properties of the parent population, as illustrated by the proportion of participants choosing the answer (c) in their 1972 study. Such thinking reflects use of the representativeness heuristic, whereby someone will judge the likelihood of an uncertain event based on how similar it is to characteristics of the parent population of events.
Birth order
- (a). What is your estimate of the number of families surveyed in which the exact order of births was BGBBBB?
- (b). In the same survey set, which, if any, of the following two sequences would be more likely: BBBGGG or GBBGBG?
All of the events listed in the problem have an equal probability, so the correct answer to (a) is 72, and to (b) is “neither is more likely”. Kahneman and Tversky [ 23 ] reported that 75 of 92 participants judged the sequence in (a) as less likely than the given sequence. A similar number (unspecified by Kahneman and Tversky, but the statistical effect was reported to be of the same order as in (a)) reported that GBBGBG was the more likely sequence. Again, Kahneman and Tversky suggested that these results reflected use of the representativeness heuristic. In the context of this problem, the heuristic would have taken the following form: some birth orders appear less patterned than others, and less patterned is to be associated with the randomness of birth order, making them more likely.
Coin tosses
- (a). H T H T H T H T
- (b). H H H H T T T T
- (c). T T H H T T H H
- (d). H T T H T H H T
- (e). all of the above are equally likely
The correct answer in this problem is (e). Kahneman and Tversky [ 23 ] reported that participants tend to choose less patterned looking sequences (e.g., H T T H T H H T) as more likely than more systematic looking sequences (e.g., H T H T H T H T). This reasoning again reflects the representativeness heuristic.
Three further questions from the literature were included to test problem solving skill.
Two drivers
- (a). Driver A would win the race
- (b). Driver B would win the race
- (c). the two drivers would arrive at the same time (within a few seconds of one another)
This problem was developed by Pelham and Neter [ 25 ]. The correct answer is (a), which can be determined by calculations of driving times for each Driver, using time = distance/velocity. Pelham and Neter argue, however, that (c) is intuitively appealing, on the basis that both drivers appear to have the same overall average speed. Pelham and Neter reported that 67% of their sample gave this incorrect response to the problem, and a further 13% selected (b).
Petrol station
Imagine that you are driving along the road and you notice that your car is running low on petrol. You see two petrol stations next to each other, both advertising their petrol prices. Station A’s price is 65c/litre; Station B’s price is 60c/litre. Station A’s sign also announces: “5c/litre discount for cash!” Station B’s sign announces “5c/litre surcharge for credit cards.” All other factors being equal (for example, cleanliness of the stations, number of cars waiting at each etc), to which station would you choose to go, and why?
This problem was adapted from one described by Galotti [ 26 ], and is inspired by research reported by Thaler [ 27 ]. According to Thaler’s research, most people prefer Station A, even though both stations are offering the same deal: 60c/litre for cash, and 65c/litre for credit. Tversky and Kahneman [ 28 ] explain this preference by invoking the concept of framing effects. In the context of this problem, such an effect would involve viewing the outcomes as changes from some initial point. The initial point frames the problem, and provides a context for viewing the outcome. Thus, depending on the starting point, outcomes in this problem can be viewed as either a gain (in Station A, you gain a discount if you use cash) or a loss (in Station B, you are charged more (a loss) for using credit). Given that people are apparently more concerned about a loss than a gain [ 29 ], the loss associated with Station B makes it the less attractive option, and hence the preference for Station A. The correct answer, though, is that the stations are offering the same deal and so no station should be preferred.
And finally, a question described by Stanovich [ 30 , 31 ] as testing our predisposition for cognitive operations that require the least computational effort.
Jack looking at Anne
- (c). Cannot be determined
Stanovich reported that over 80% of people choose the “lazy” answer (c). The correct answer is (a).
The above questions survey, in a clear problem solving setting, an ability to engage advanced cognitive processing in order to critically evaluate and possibly override initial gut reasoning, an ability to reason about probability within the framework of the law of large numbers and the relationship between randomness and patterning, an ability to isolate salient features of a problem and, with the last question in particular, an ability to map logical relations. It might be hypothesised that according to degrees of mathematical training, in line with the knowledge base provided and the claims of associated broad and enhanced problem-solving abilities in general, that participants with greater degrees of such training would outperform others on these questions. This hypothesis was investigated in this study. In addition, given that no previous study on this issue has examined the variety of problems used in this study, we also undertook an exploratory analysis to investigate whether there exist any associations between the problems in terms of their likelihood of correct solution. Similarities between problems might indicate which problem solving domains could be susceptible to the effects of mathematics training.
- Introductory—First year, second semester, university students with weak high school mathematical results, only enrolled in the current unit as a compulsory component for their chosen degree, a unit not enabling any future mathematical pathway, a typical student may be enrolled in a Biology or Geography major;
- Standard—First year, second semester, university students with fair to good high school mathematical results, enrolled in the current mathematics unit as a compulsory component for their chosen degree with the possibility of including some further mathematical units in their degree pathway, a typical student may be enrolled in an IT or Computer Science major;
- Advanced1—First year, second semester, university mathematics students with very strong interest as well as background in mathematics, all higher year mathematical units are included as possible future pathway, a typical student may be enrolled in a Mathematics or Physics major;
- Advanced2—Second year, second semester, university mathematics students with strong interest as well as background in mathematics, typically a direct follow on from the previously mentioned Advanced1 cohort;
- Academic—Research academics in the mathematical sciences.

Participants
123 first year university students volunteered during “help on demand” tutorial times containing up to 30 students. These are course allocated times that are supervised yet self-directed by students. This minimised disruption and discouraged coercion. 44 second year university students completed the questionnaire during a weekly one-hour time slot dedicated to putting the latest mathematical concepts to practice with the lecturer (whereby contrast to what occurs in tutorial times the lecturer does most of the work and all students enrolled are invited). All these university students completed the questionnaire in normal classroom conditions; they were not placed under strict examination conditions. The lead author walked around to prevent discussion and coercion and there was minimum disruption. 30 research academics responded to local advertising and answered the questionnaire in their workplace while supervised.
The questionnaires were voluntary, anonymous and confidential. Participants were free to withdraw from the study at any time and without any penalty. No participant took this option however. The questionnaires gathered demographic information which included age, level of education attained and current qualification pursued, name of last qualification and years since obtaining it, and an option to note current speciality for research academics. Each problem task was placed on a separate page. Participants were not placed under time constraint, but while supervised, were asked to write their start and finish times on the front page of the survey to note approximate completion times. Speed of completion was not incentivised. Participants were not allowed to use calculators. A final “Comments Page” gave the option for feedback including specifically if the participants had previously seen any of the questions. Questionnaires were administered in person and supervised to avoid collusion or consulting of external sources.
The responses were coded four ways: A) correct; B) standard error (the errors discussed above in The Study); C) other error; D) left blank.
The ethical aspects of the study were approved by the Human Research Ethics Committee of the University of Sydney, protocol number [2016/647].
The first analysis examined the total number of correct responses provided by the participants as a function of group. Scores ranged from 1 to 11 out of a total possible of 11 (Problem 6 had 2 parts) ( Fig 1 ). An ANOVA of this data indicated a significant effect of group (F(4, 192) = 20.426, p < .001, partial η 2 = .299). Pairwise comparisons using Tukey’s HSD test indicated that the Introductory group performed significantly worse than the Advanced1, Advanced2 and Academic groups. There were no significant differences between the Advanced1, Advanced2 and Academic groups.
- PPT PowerPoint slide
- PNG larger image
- TIFF original image
Error bars are one standard error of the mean.
https://doi.org/10.1371/journal.pone.0236153.g001
Overall solution time, while recorded manually and approximately, was positively correlated with group, such that the more training someone had received, the longer were these solution times (r(180) = 0.247, p = .001). However, as can be seen in Fig 2 , this relationship is not strong.
https://doi.org/10.1371/journal.pone.0236153.g002
A series of chi-squared analyses, and their Bayesian equivalents, were performed on each problem, to determine whether the distribution of response types differed as a function of group. To minimise the number of cells in which expected values in some of these analyses were less than 5, the Standard Error, Other Error and Blank response categories were collapsed into one category (Incorrect Response). For three of the questions, the expected values of some cells did fall below 5, and this was due to most people getting the problem wrong (Four Cards), or most people correctly responding to the problem (Bat and Ball, Coin Tosses). In these cases, the pattern of results was so clear that a statistical analysis was barely required. Significant chi-squared results were examined further with pairwise posthoc comparisons (see Table 1 ).
https://doi.org/10.1371/journal.pone.0236153.t001
The three groups with the least amount of training in mathematics were far less likely than the other groups to give the correct solution (χ 2 (4) = 31.06, p < .001; BF 10 = 45,045) ( Table 1 ). People in the two most advanced groups (Advanced2 and Academic) were more likely to solve the card problem correctly, although it was still less than half of the people in these groups who did so. Further, these people were less likely to give the standard incorrect solution, so that most who were incorrect suggested some more cognitively elaborate answer, such as turning over all cards. The proportion of people in the Advanced2 and Academic groups (39 and 37%) who solved the problem correctly far exceeded the typical proportion observed with this problem (10%). Of note, also, is the relatively high proportion of those in the higher training groups who, when they made an error, did not make the standard error, a similar result to the one reported by Inglis and Simpson [ 11 ].
The cognitive reflection test
In the Lily Pads problem, although most people in the Standard, Advanced1, Advanced2 and Academic groups were likely to select the correct solution, it was also the case that the less training someone had received in mathematics, the more likely they were to select an incorrect solution (χ 2 (4) = 27.28, p < .001; BF 10 = 15,554), with the standard incorrect answer being the next most prevalent response for the two lower ability mathematics groups ( Table 1 ).
Performance on the Widgets problem was similar to performance on the Lily Pads problem in that most people in the Standard, Advanced1, Advanced2 and Academic groups were likely to select the correct solution, but that the less training someone had received in mathematics, the more likely they were to select an incorrect solution (χ 2 (4) = 23.76, p< .001; BF 10 = 516) ( Table 1 ). As with the Lily Pads and Widget problems, people in the Standard, Advanced1, Advanced2 and Academic groups were highly likely to solve the Bat and Ball problem (χ 2 (4) = 35.37, p < .001; BF 10 = 208,667). Errors were more likely from the least mathematically trained people (Introductory, Standard) than the other groups ( Table 1 ).
To compare performance on the CRT with previously published results, performance on the three problems (Lily Pads, Widgets, Bat and Ball) were combined. The number of people in each condition that solved 0, 1, 2, or 3 problems correctly is presented in Table 2 . The Introductory group were evenly distributed amongst the four categories, with 26% solving all three problems correctly. Around 70% of the rest of the groups solved all 3 problems correctly, which is vastly superior to the 17% reported by Frederick [ 16 ].
https://doi.org/10.1371/journal.pone.0236153.t002
Responses to the Hospitals problem were almost universally split between correct and standard errors in the Standard, Advanced1, Advanced2 and Academic groups. Although this pattern of responses was also evident in the Introductory group, this group also exhibited more non-standard errors and non-responses than the other groups. However, the differences between the groups were not significant (χ 2 (4) = 4.93, p = .295; BF 10 = .068) ( Table 1 ). Nonetheless, the performance of all groups exceeds the 20% correct response rate reported by Kahneman and Tversky [ 23 ].
The two versions of the Birth Order problem showed similar results, with correct responses being more likely in the groups with more training (i.e., Advanced1, Advanced2 and Academic), and responses being shared amongst the various categories in the Introductory and Standard groups (χ a 2 (4) = 24.54, p < .001; BF 10 = 1,303; χ b 2 (4) = 25.77, p < .001; BF 10 = 2,970) ( Table 1 ). Nonetheless, performance on both versions of the problem in this study was significantly better than the 82% error rate reported by Kahneman and Tversky [ 23 ].
The Coin Tosses problem was performed well by all groups, with very few people in any condition committing errors. There were no obvious differences between the groups (χ 2 (4) = 3.70, p = .448; BF 10 = .160) ( Table 1 ). Kahneman and Tversky [ 23 ] reported that people tend to make errors on this type of problem by choosing less patterned looking sequences, but they did not report relative proportions of people making errors versus giving correct responses. Clearly the sample in this study did not perform like those in Kahneman and Tversky’s study.
Responses on the Two Drivers problem were clearly distinguished by a high chance of error in the Introductory and Standard groups (over 80%), and a fairly good chance of being correct in the Advanced1, Advanced2 and Academic groups (χ 2 (4) = 46.16, p < .001; BF 10 = 1.32 x 10 8 ) ( Table 1 ). Academics were the standout performers on this problem, although over a quarter of this group produced an incorrect response. Thus, the first two groups performed similarly to the participants in the Pelham and Neter [ 25 ] study, 80% of whom gave an incorrect response.
Responses on the Petrol Station problem were marked by good performance by the Academic group (73% providing a correct response), and just over half of each of the other groups correctly solving the problem. This difference was not significant (χ 2 (4) = 4.68, p = .322: BF 10 = .059) ( Table 1 ). Errors were fairly evenly balanced between standard and other, except for the Academic group, who were more likely to provide a creative answer if they made an error. Thaler [ 27 ] reported that most people get this problem wrong. In this study, however, on average, most people got this problem correct, although this average was boosted by the Academic group.
Responses on the Jack looking at Anne problem generally were standard errors, except for the Advanced2 and Academic groups, which were evenly split between standard errors and correct responses (χ 2 (4) = 18.03, p = .001; BF 10 = 46) ( Table 1 ). Thus, apart from these two groups, the error rate in this study was similar to that reported by Stanovich [ 30 ], where 80% of participants were incorrect.
A series of logistic regression analyses were performed in order to examine whether the likelihood of solving a particular problem correctly could be predicted on the basis of whether other problems were solved correctly. Each analysis involved selecting performance (correct or error) on one problem as the outcome variable, and performance on the other problems as predictor variables. Training (amount of training) was also included as a predictor variable in each analysis. A further logistic regression was performed with training as the outcome variable, and performance on all of the problems as predictor variables. The results of these analyses are summarised in Table 3 . There were three multi-variable relationships observed in these analyses, which can be interpreted as the likelihood of solving one problem in each group being associated with solving the others in the set. These sets were: (1) Lily Pads, Widgets and Petrol Station; (2) Hospitals, Four Cards and Two Drivers; (3) Birth Order and Coin Tosses. Training also featured in each of these sets, moderating the relationships as per the results presented above for each problem.
https://doi.org/10.1371/journal.pone.0236153.t003
The final “Comments Page” revealed the participants as overwhelmingly enjoying the questions. Any analysis of previous exposure to the tasks proved impossible as there was little to no alignment on participant’s degree of recall, if any, and even perceptions of what exposure entailed. For example, some participants confused being exposed to the particular tasks with being habitually exposed to puzzles, or even mathematics problems, more broadly.
In general, the amount of mathematics training a group had received predicted their performance on the overall set of problems. The greater the training, the more problems were answered correctly, and the slower the recorded response times. There was not an obvious difference between the Advanced1, Advanced2 and Academic groups on either of these measures, however there were clear differences between this group and the Introductory and Standard groups, with the former exhibiting clearly superior accuracy. While time records were taken approximately, so as to avoid adding time pressure as a variable, that the Advanced1, Advanced2 and Academic groups recorded more time in their consideration of the problems, may suggest a “pause and consider” approach to such problems is a characteristic of the advanced groups. This is in line with what was suggested by an eye-movement tracking study of mathematically trained students attempting the Four Cards Problem; where participants that had not chosen the standard error had spent longer considering the card linked to the matching bias effect [ 14 ]. It is important to note, however, that longer response times may reflect other cognitive processes than deliberation [ 32 ].
Performance on some problems was associated with performance on other problems. That is, if someone correctly answered a problem in one of these sets, they were also highly likely to correctly answer the other problems in the set. These sets were: (1) Lily Pads, Widgets and Petrol Station; (2) Hospitals, Four Cards and Two Drivers; (3) Birth Order and Coin Tosses. This is different with how these problems have been typically clustered a priori in the research literature: (I) Lily Pads, Widgets and Bat and Ball (CRT); (II) Hospitals and Two Drivers (explained below); (III) Hospitals, Birth Order and Coin Tosses (representativeness heuristic); (IV) Birth Order and Coin Tosses (probability theory). Consideration of these problem groupings follows.
Correctly answering all three problems in (I) entailed not being distracted by particular pieces of information in the problems so as to stay focused on uncovering the real underlying relationships. The Lily Pads and Widget problems can mislead if attention is over focused on the numbers, and conversely, the Petrol Station problem can mislead if there is too much focus on the idea of a discount. While the Lily Pads and Widget problems are traditionally paired with the Bat and Ball problem in the CRT, it may be that performance on the Bat and Ball problem did not appear as part of this set due to an added level of difficulty. With the problems in (I), avoiding being distracted by certain parts of the questions at the expense of others almost leads directly to the correct answer. However, with the Bat and Ball problem, further steps in mathematical reasoning still need to occur in answering which two numbers add together to give a result while also subtracting one from the other for another.
With the problems in (II) it is of interest that the Two Drivers problem was created specifically to be paired with the Hospitals problem to test for motivation in problem solving [ 23 ]. Within this framework further transparent versions of these problems were successfully devised to manipulate for difficulty. The Two Drivers problem was amended to have Driver B travelling at exactly 5 mph during the first half of the race and at exactly 95 mph during the last half of the race. The Hospitals problem was amended so the smaller hospital would have “only 2” babies born each day and where for a period of one year the hospitals recorded the number of days on which all of the babies born were boys. Could the association in (II) be pointing to how participants overcome initial fictitious mathematical rules? Maybe they reframe the question in simpler terms to see the pattern. The Four Cards Problem also elicited a high number of incorrect answers where, associated with mathematical training, the standard incorrect solution was avoided for more cognitively elaborate ones. Indeed, a gradation effect appeared across the groups where the standard error of the “D and 3” cards becomes “D only” ( Table 4 ). Adrian Simpson and Derrick Watson found a comparable result across their two groups [14 p61]. This could again be pointing to having avoided an initial fictitious rule of simply concentrating on items directly found in the question, participants then seek to reframe the question to unearth the logical rule to be deduced. An added level of difficulty with this question may be why participants become trapped in a false answer. The eye-movement tracking study mentioned above supports this theory.
https://doi.org/10.1371/journal.pone.0236153.t004
The problems in (III) fit naturally together as part of basic probability theory, a topic participants would have assimilated, or not, as part of various education curricula. While the equal likelihood of all possible outcomes with respect to a coin toss may be culturally assimilated, the same may not be as straightforward for birth gender outcomes where such assumptions could be swayed by biological hypothesis or folk wisdom [ 33 ]. The gradation of the results in terms of mathematical training does not support this possibility.
The effect of training on performance accuracy was more obvious in some problems compared to others, and to some extent, this was related to the type of problem. For instance, most of the problems in which performance was related to training (Four Cards, CRT [Lily Pads, Widgets, Bat and Ball], Two Drivers, Jack looking at Anne) could be classed as relying on logical and/or critical thinking. The one exception was the Birth Order problems, which are probability related.
In contrast, two of the three problems in which training did not appear to have much impact on performance (Hospitals and Coin Tosses) require domain-specific knowledge. The Hospitals problem requires a degree of knowledge about sampling statistics. This is a topic of quite distinct flavour that not all mathematically trained individuals gain familiarity with. On the other hand, all groups having performed well on the Coin Tosses problem is in line with a level of familiarity with basic probability having been originally presented at high school. While the questioning of patterning as negatively correlated with randomness is similar to that appearing in the Birth Order question, in the Birth Order question this aspect is arguably more concealed. These results and problem grouping (III) could be pointing to an area for improvement in teaching where the small gap in knowledge required to go from answering the Coin Tosses problem correctly to achieving similarly with the Birth Order problem could be easily addressed. A more formal introduction to sampling statistics in mathematical training could potentially bridge this gap as well as further be extended towards improvement on the Hospitals problem.
The other problem where performance was unrelated to training, the Petrol Station problem, cannot be characterised similarly. It is more of a logical/critical thinking type problem, where there remains some suggestion that training may have impacted performance, as the Academic group seemed to perform better than the rest of the sample. An alternate interpretation of this result is therefore that this problem should not be isolated but grouped with the other problems where performance is affected by training.
- The Introductory group’s mathematics high school syllabus studied prior to first semester course entry covered: Functions, Trigonometric Functions, Calculus (Introduction to Differentiation, Applications of the Derivative, Antiderivatives, Areas and the Definite Integral), Financial Mathematics, Statistical Analysis. The Introductory group then explored concepts in mathematical modelling with emphasis on the importance of calculus in their first semester of mathematical studies.
- The Standard group’s mathematics high school syllabus studied prior to first semester course entry covered: Functions, Trigonometric Functions, Calculus (Rates of Change, Integration including the method of substitution, trigonometric identities and inverse trigonometric functions, Areas and Volumes of solids of revolution, some differential equations), Combinatorics, Proof (with particular focus on Proof by Mathematical Induction), Vectors (with application to projectile motion), Statistical Analysis. In first semester their mathematical studies then covered a number of topics the Advanced1 group studied prior to gaining entrance at university; further details on this are given below.
- The Advanced1 group’s mathematics high school syllabus studied prior to first semester course entry covered: the same course content the Standard group covered at high school plus extra topics on Proof (develop rigorous mathematical arguments and proofs, specifically in the context of number and algebra and further develop Proof by Mathematical Induction), Vectors (3 dimensional vectors, vector equations of lines), Complex Numbers, Calculus (Further Integration techniques with partial fractions and integration by parts), Mechanics (Application of Calculus to Mechanics with simple harmonic motion, modelling motion without and with resistance, projectiles and resisted motion). The Standard group cover these topics in their first semester university studies in mathematics with the exclusion of further concepts of Proof or Mechanics. In first semester the Advanced1 group have built on their knowledge with an emphasis on both theoretical and foundational aspects, as well as developing the skill of applying mathematical theory to solve practical problems. Theoretical topics include a host of theorems relevant to the study of Calculus.
In summary, at the point of our study, the Advanced1 group had more knowledge and practice on rigorous mathematical arguments and proofs in the context of number and algebra, and more in-depth experience with Proofs by Induction, but the bulk of extra knowledge rests with a much deeper knowledge of Calculus. They have had longer experience with a variety of integration techniques, and have worked with a variety of applications of calculus to solve practical problems, including a large section on mechanics at high school. In first semester at university there has been a greater focus on theoretical topics including a host of theorems and associated proofs relevant to the topics studied. As compared to the Introductory and Standard groups, the Advanced1 group have only widened the mathematics knowledge gap since their choice of post-compulsory mathematics at high school. The Advanced2 group come directly from an Advanced1 cohort. And the Academics group would have reached the Advanced1 group’s proficiency as part of their employment. So, are specific reasoning skills resulting from this level of abstract reasoning? Our findings suggest this should certainly be an area of investigation and links in interestingly with other research work. In studying one of the thinking tasks in particular (the Four Cards Problem) and its context of conditional inference more specifically, Inglis and Simpson [ 15 ] found a clear difference between undergraduates in mathematics and undergraduates in other university disciplines, yet also showed a lack of development over first-year university studies on conditional inference measures. A follow up study by Attridge and Inglis [ 22 ] then zeroed in on post-compulsory high school mathematical training and found that students with such training did develop their conditional reasoning to a greater extent than their control group over the course of a year, despite them having received no explicit tuition in conditional logic. The development though, whilst demonstrated as not being the result of a domain-general change in cognitive capacity or thinking disposition, and most likely associated with the domain-specific study of mathematics, revealed a complex pattern of endorsing more of some inferences and less of others. The study here focused on a much broader problem set associated with logical and critical thinking and it too is suggestive of a more complex picture in how mathematics training may be contributing to problem solving styles. A more intricate pattern to do with the impact of mathematical training on problem solving techniques is appearing as required for consideration.
There is also a final interpretation to consider: that people in the Advanced 1, Advanced2 and Academic groups did not gain anything from their mathematics training in terms of their ability to solve these problems. Instead, with studies denying any correlation of many of these problems with what is currently measured as intelligence [ 30 ], they might still be people of a particular intelligence or thinking disposition to start with, who have been able to use that intelligence to not only solve these problems, but also survive the challenges of their mathematics training.
That the CRT has been traditionally used as a measure of baseline thinking disposition and that performance has been found to be immutable across groups tested is of particular interest since our results show a clear possible training effect on these questions. CRT is tied with a willingness to engage in effortful thinking which presents as a suitable ability for training. It is beyond the scope of this study, but a thorough review of CRT testing is suggestive of a broader appreciation and better framework to understand thinking disposition, ability and potential ability.
Mathematical training appears associated with certain thinking skills, but there are clearly some subtleties that need to be extricated. The thinking tasks here add to the foundational results where the aim is for a firmer platform on which to eventually base more targeted and illustrative inquiry. If thinking skills can be fostered, could first year university mathematics teaching be improved so that all samples from that group reach the Advanced1 group level of reasoning? Do university mathematics courses become purely about domain-specific knowledge from this point on? Intensive training has been shown to impact the brain and cognition across a number of domains from music [ 34 ], to video gaming [ 35 ], to Braille reading [ 36 ]. The hypothesis that mathematics, with its highly specific practice, fits within this list remains legitimate, but simply unchartered. With our current level of understanding it is worth appreciating the careful wording of the NYU Courant Institute on ‘Why Study Math?’ where there is no assumption of causation: “Mathematicians need to have good reasoning ability in order to identify, analyze, and apply basic logical principles to technical problems.” [ 37 ].
Limitations
One possible limitation of the current study is that the problems may have been too easy for the more advanced people, and so we observed a ceiling effect (i.e., some people obtained 100% correct on all problems). This was most obvious in the Advanced1, Advanced2 and Academic groups. It is possible that participants in these groups had developed logical and critical thinking skills throughout their mathematical training that were sufficient to cope with most of the problems used in this study, and so this would support the contention that training in mathematics leads to the development of logical and critical thinking skills useful in a range of domains. Another interpretation is that participants in these groups already possessed the necessary thinking skills for solving the problems in this study, which is why they are able to cope with the material in the advanced units they were enrolled in, or complete a PhD in mathematics and hold down an academic position in a mathematics department. This would then suggest that training in mathematics had no effect on abstract thinking skills—people in this study possessed them to varying extents prior to their studies. This issue might be settled in a future study that used a greater number of problems of varying difficulties to maximise the chances of finding a difference between the three groups with the most amount of training. Alternatively, a longitudinal study that followed people through their mathematics training could determine whether their logical and critical thinking abilities changed throughout their course.
A further limitation of the study may be that several of the reasoning biases examined in this study were measured by only one problem each (i.e., Four Cards Problem, Two Drivers, Petrol Station, Jack looking at Anne). A more reliable measure of these biases could be achieved by including more problems that tap into these biases. This would, however, increase the time required of participants during data collection, and in the context of this study, would mean a different mode of testing would likely be required.
Broad sweeping intuitive claims of the transferable skills endowed by a study of mathematics require evidence. Our study uniquely covers a wide range of participants, from limited mathematics training through to research academics in the mathematical sciences. It furthermore considered performance on 11 well-studied thinking tasks that typically elude participants in psychological studies and on which results have been uncorrelated with general intelligence, education levels and other demographic information [ 15 , 16 , 30 ]. We identified different performances on these tasks with respect to different groups, based on level of mathematical training. This included the CRT which has developed into a method of measuring baseline thinking disposition. We identified different distributions of types of errors for the mathematically trained. We furthermore identified a performance threshold that exists in first year university for those with high level mathematics training. This study then provides insight into possible changes and adjustments to mathematics courses in order for them to fulfil their advertised goal of reaching improved rational and logical reasoning for a higher number of students.
It is central to any education program to have a clear grasp of the nature of what it delivers and how, but arguably especially so for the core discipline that is mathematics. In 2014 the Office of The Chief Scientist of Australia released a report “Australia’s STEM workforce: a survey of employers” where transferable skills attributed to mathematics were also ones that employers deemed as part of the most valuable [ 38 ]. A better understanding of what mathematics delivers in this space is an opportunity to truly capitalise on this historical culture-crossing subject.
Supporting information
https://doi.org/10.1371/journal.pone.0236153.s001
Acknowledgments
The authors would like to thank Jacqui Ramagge for her proof reading and input, as well as support towards data collection.
- 1. Smith A. Making mathematics count: The report of Professor Adrian Smith’s inquiry into post-14 mathematics education. 2004. London: The Stationery Office.
- 2. AMSI, Vision for a Maths Nation. 2015. http://amsi.org.au/publications/a-vision-for-a-maths-nation/
- 3. British Columbia [Internet]. Mathematics; Goals and Rationale. 2016 [cited 2019 Dec 5]. https://curriculum.gov.bc.ca/curriculum/mathematics/core/goals-and-rationale
- 4. Monash University [Internet]. Mathematical Sciences. 2019 [cited 2019 Jul 30]. https://www.monash.edu/science/schools/mathematical-sciences/current .
- 5. The University of Sydney [Internet]. MATH1014. 2017 [cited 2019 Dec 5]. http://www.maths.usyd.edu.au/u/UG/TU/YR1ADMIN/r/MATH1014.pdf .
- 6. The University of Sydney [Internet]. MATH2965. 2016 [cited 2016 Dec 12]. http://www.maths.usyd.edu.au/u/UG/IM/MATH2965/
- 7. The University of Sydney [Internet]. MATH3066. 2017 [cited 2017 Dec 8]. http://www.maths.usyd.edu.au/u/UG/SM/MATH3066/r/2017info3066.pdf .
- 8. Cambridge University [Internet]. Mathematical Tripos. 2019 [cited 2019 Jul 30]. https://www.maths.cam.ac.uk/undergrad/course/transferable_skills .
- 9. Speelman CP, Kirsner K. Beyond the learning curve: The construction of mind. Oxford: Oxford University Press; 2005.
- 10. Fadel C. Mathematics for the 21 st Century: What Should Students Learn? Boston, Massachusetts: Center for Curriculum Redesign; 2014.
- 11. Inglis M, Simpson A. Heuristic biases in mathematical reasoning. In: Chick HL, Vincent JL, editors. Proceedings of the 29th Conference of the International Group for the Psychology of Mathematics Education. Melbourne: PME; 2005. p. 177–84.
- 12. Manktelow KI. Reasoning and Thinking. UK: Psychology Press; 1999.
- View Article
- PubMed/NCBI
- Google Scholar
- 14. Inglis M, Attridge N. Does mathematical study develop logical thinking? Testing the theory of formal discipline. London: World Scientific Publishing Europe Ltd; 2016.
- 24. Nisbett RE. Can reasoning be taught? In: Callan E, Grotzer T, Kagan J, Nisbett RE, Perkins DN, Shulman LS, editors. Education and a Civic Society: Teaching Evidence-based Decision Making. Cambridge, MA: American Academy of Arts & Sciences; 2009.
- 26. Galotti KM. Cognitive psychology in and out of the laboratory. Belmont, CA: Brooks/Cole; 1994.
- 37. NYU [Internet]. Why Study Math? 2019 [cited 2019 Jul 30]. https://math.nyu.edu/dynamic/undergrad/overview/why-study-math/
- 38. Office of The Chief Scientist. Australia’s STEM workforce: a survey of employers. Barton ACT: Deloitte Access Economics; 2014.
Increasing Critical Thinking Skills in Math
- Math , Planning
It’s important that we are building critical thinking skills in math. Too often these are overlooked or assumed that students do it because they have to problem solve sometimes. While that does help build the all-important critical thinking skills, we need to make sure we are also finding ways to purposely bring it into instruction.
One such way that I like to implement critical thinking skills in my math class is through a game called Puzzlers. Recently I discussed why you should use games in the classroom and this one is no exception. Games go beyond just having fun and “entertaining” students. They aren’t just fillers.

Building Critical Thinking Skills with the Puzzler Game
The puzzler game is a game that not only increases critical thinking skills, but it also practices both fact fluency and the order of operations!
In the puzzler game, students are given a target number. This happens by rolling a die or dice, but it can also be any chosen number between 1 and 36. For instance, I have randomly chosen the date before.
Next, students are provided with a 3×3 grid of the numbers 1 through 9 mixed up. (See the image below.)

Once students have their target number and a mixed up grid of the numbers 1-9, they are ready to begin. This is where the critical thinking skills will come in.
Now, students will need to come up with a way to use ONLY three numbers (in a row, diagonally, or in a column) to get that target number. They will do this by creating equations that total the target number. They can add, subtract, multiply, divide, or even come up with a combination of them. If needed, they can use parentheses. This is where knowing the order of operations is necessary!
For instance, let’s take the example above with the 9 numbers on the sticky notes. Let’s say that the target number was 18. The student could create these two equations to come up with the solution of the target number 18:
- (9 x 6) ÷ 3
- (9 + 8) – 1
Here’s an example of a puzzler card with multiple solutions:

What I love about this puzzler game is the variety of ways it can be used to help build critical thinking skills! For instance, students could list all of the equations, or solutions, to get the target number:

or go through multiple cards trying to list as many solutions as they can:

Or they could skip rolling the dice altogether and see how many solutions they can find for the target numbers one through ten. Why not even through in zero?!

Students love this game and it’s perfect for independent work, early finishers, small groups, and even enrichment. It’s differentiated and there are cards that are strictly for adding and subtracting for students who can’t multiply yet.
You don’t have to purchase my puzzler resource to play this critical thinking skills builder! You can easily create it in your classroom as a bulletin board and change out the numbers each day!
If you want to save some time, grab the extra differentiated materials, and the specifics, head to my store now to purchase it! It’s definitely worth it!

Click here to purchase this Puzzler Game.
FIND IT NOW!
Check me out on tpt.

CHECK THESE OUT

Three Types of Rocks and Minerals with Rock Cycle Circle Book

Partitioning Shapes Equal Share Fractions Halves, Thirds, Fourths Math Puzzles
Want to save time?
COPYRIGHT © 2016-2024. The Owl Teacher | Privacy page | Disclosure Page | Shipping | Returns/Refunds
BOGO on EVERYTHING!
High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
Free ready-to-use math resources
Hundreds of free math resources created by experienced math teachers to save time, build engagement and accelerate growth

20 Effective Math Strategies To Approach Problem-Solving
Katie Keeton
Math strategies for problem-solving help students use a range of approaches to solve many different types of problems. It involves identifying the problem and carrying out a plan of action to find the answer to mathematical problems.
Problem-solving skills are essential to math in the general classroom and real-life. They require logical reasoning and critical thinking skills. Students must be equipped with strategies to help them find solutions to problems.
This article explores mathematical problem solving strategies, logical reasoning and critical thinking skills to help learners with solving math word problems independently in real-life situations.
What are problem-solving strategies?
Problem-solving strategies in math are methods students can use to figure out solutions to math problems. Some problem-solving strategies:
- Draw a model
- Use different approaches
- Check the inverse to make sure the answer is correct
Students need to have a toolkit of math problem-solving strategies at their disposal to provide different ways to approach math problems. This makes it easier to find solutions and understand math better.
Strategies can help guide students to the solution when it is difficult ot know when to start.

The ultimate guide to problem solving techniques
Download these ready-to-go problem solving techniques that every student should know. Includes printable tasks for students including challenges, short explanations for teachers with questioning prompts.
20 Math Strategies For Problem-Solving
Different problem-solving math strategies are required for different parts of the problem. It is unlikely that students will use the same strategy to understand and solve the problem.
Here are 20 strategies to help students develop their problem-solving skills.
Strategies to understand the problem
Strategies that help students understand the problem before solving it helps ensure they understand:
- The context
- What the key information is
- How to form a plan to solve it
Following these steps leads students to the correct solution and makes the math word problem easier .
Here are five strategies to help students understand the content of the problem and identify key information.
1. Read the problem aloud
Read a word problem aloud to help understand it. Hearing the words engages auditory processing. This can make it easier to process and comprehend the context of the situation.
2. Highlight keywords
When keywords are highlighted in a word problem, it helps the student focus on the essential information needed to solve it. Some important keywords help determine which operation is needed. For example, if the word problem asks how many are left, the problem likely requires subtraction. Ensure students highlight the keywords carefully and do not highlight every number or keyword. There is likely irrelevant information in the word problem.
3. Summarize the information
Read the problem aloud, highlight the key information and then summarize the information. Students can do this in their heads or write down a quick summary. Summaries should include only the important information and be in simple terms that help contextualize the problem.
4. Determine the unknown
A common problem that students have when solving a word problem is misunderstanding what they are solving. Determine what the unknown information is before finding the answer. Often, a word problem contains a question where you can find the unknown information you need to solve. For example, in the question ‘How many apples are left?’ students need to find the number of apples left over.
5. Make a plan
Once students understand the context of the word problem, have dentified the important information and determined the unknown, they can make a plan to solve it. The plan will depend on the type of problem. Some problems involve more than one step to solve them as some require more than one answer. Encourage students to make a list of each step they need to take to solve the problem before getting started.
Strategies for solving the problem
1. draw a model or diagram.
Students may find it useful to draw a model, picture, diagram, or other visual aid to help with the problem solving process. It can help to visualize the problem to understand the relationships between the numbers in the problem. In turn, this helps students see the solution.

Similarly, you could draw a model to represent the objects in the problem:

2. Act it out
This particular strategy is applicable at any grade level but is especially helpful in math investigation in elementary school . It involves a physical demonstration or students acting out the problem using movements, concrete resources and math manipulatives . When students act out a problem, they can visualize and contectualize the word problem in another way and secure an understanding of the math concepts. The examples below show how 1st-grade students could “act out” an addition and subtraction problem:
| The problem | How to act out the problem |
| Gia has 6 apples. Jordan has 3 apples. How many apples do they have altogether? | Two students use counters to represent the apples. One student has 6 counters and the other student takes 3. Then, they can combine their “apples” and count the total. |
| Michael has 7 pencils. He gives 2 pencils to Sarah. How many pencils does Michael have now? | One student (“Michael”) holds 7 pencils, the other (“Sarah”) holds 2 pencils. The student playing Michael gives 2 pencils to the student playing Sarah. Then the students count how many pencils Michael is left holding. |
3. Work backwards
Working backwards is a popular problem-solving strategy. It involves starting with a possible solution and deciding what steps to take to arrive at that solution. This strategy can be particularly helpful when students solve math word problems involving multiple steps. They can start at the end and think carefully about each step taken as opposed to jumping to the end of the problem and missing steps in between.
For example,

To solve this problem working backwards, start with the final condition, which is Sam’s grandmother’s age (71) and work backwards to find Sam’s age. Subtract 20 from the grandmother’s age, which is 71. Then, divide the result by 3 to get Sam’s age. 71 – 20 = 51 51 ÷ 3 = 17 Sam is 17 years old.
4. Write a number sentence
When faced with a word problem, encourage students to write a number sentence based on the information. This helps translate the information in the word problem into a math equation or expression, which is more easily solved. It is important to fully understand the context of the word problem and what students need to solve before writing an equation to represent it.
5. Use a formula
Specific formulas help solve many math problems. For example, if a problem asks students to find the area of a rug, they would use the area formula (area = length × width) to solve. Make sure students know the important mathematical formulas they will need in tests and real-life. It can help to display these around the classroom or, for those who need more support, on students’ desks.
Strategies for checking the solution
Once the problem is solved using an appropriate strategy, it is equally important to check the solution to ensure it is correct and makes sense.
There are many strategies to check the solution. The strategy for a specific problem is dependent on the problem type and math content involved.
Here are five strategies to help students check their solutions.
1. Use the Inverse Operation
For simpler problems, a quick and easy problem solving strategy is to use the inverse operation. For example, if the operation to solve a word problem is 56 ÷ 8 = 7 students can check the answer is correct by multiplying 8 × 7. As good practice, encourage students to use the inverse operation routinely to check their work.
2. Estimate to check for reasonableness
Once students reach an answer, they can use estimation or rounding to see if the answer is reasonable. Round each number in the equation to a number that’s close and easy to work with, usually a multiple of ten. For example, if the question was 216 ÷ 18 and the quotient was 12, students might round 216 to 200 and round 18 to 20. Then use mental math to solve 200 ÷ 20, which is 10. When the estimate is clear the two numbers are close. This means your answer is reasonable.
3. Plug-In Method
This method is particularly useful for algebraic equations. Specifically when working with variables. To use the plug-in method, students solve the problem as asked and arrive at an answer. They can then plug the answer into the original equation to see if it works. If it does, the answer is correct.

If students use the equation 20m+80=300 to solve this problem and find that m = 11, they can plug that value back into the equation to see if it is correct. 20m + 80 = 300 20 (11) + 80 = 300 220 + 80 = 300 300 = 300 ✓
4. Peer Review
Peer review is a great tool to use at any grade level as it promotes critical thinking and collaboration between students. The reviewers can look at the problem from a different view as they check to see if the problem was solved correctly. Problem solvers receive immediate feedback and the opportunity to discuss their thinking with their peers. This strategy is effective with mixed-ability partners or similar-ability partners. In mixed-ability groups, the partner with stronger skills provides guidance and support to the partner with weaker skills, while reinforcing their own understanding of the content and communication skills. If partners have comparable ability levels and problem-solving skills, they may find that they approach problems differently or have unique insights to offer each other about the problem-solving process.
5. Use a Calculator
A calculator can be introduced at any grade level but may be best for older students who already have a foundational understanding of basic math operations. Provide students with a calculator to allow them to check their solutions independently, accurately, and quickly. Since calculators are so readily available on smartphones and tablets, they allow students to develop practical skills that apply to real-world situations.
Step-by-step problem-solving processes for your classroom
In his book, How to Solve It , published in 1945, mathematician George Polya introduced a 4-step process to solve problems.
Polya’s 4 steps include:
- Understand the problem
- Devise a plan
- Carry out the plan
Today, in the style of George Polya, many problem-solving strategies use various acronyms and steps to help students recall.
Many teachers create posters and anchor charts of their chosen process to display in their classrooms. They can be implemented in any elementary, middle school or high school classroom.
Here are 5 problem-solving strategies to introduce to students and use in the classroom.

How Third Space Learning improves problem-solving
Resources .
Third Space Learning offers a free resource library is filled with hundreds of high-quality resources. A team of experienced math experts carefully created each resource to develop students mental arithmetic, problem solving and critical thinking.
Explore the range of problem solving resources for 2nd to 8th grade students.
One-on-one tutoring
Third Space Learning offers one-on-one math tutoring to help students improve their math skills. Highly qualified tutors deliver high-quality lessons aligned to state standards.
Former teachers and math experts write all of Third Space Learning’s tutoring lessons. Expertly designed lessons follow a “my turn, follow me, your turn” pedagogy to help students move from guided instruction and problem-solving to independent practice.
Throughout each lesson, tutors ask higher-level thinking questions to promote critical thinking and ensure students are developing a deep understanding of the content and problem-solving skills.

Problem-solving
Educators can use many different strategies to teach problem-solving and help students develop and carry out a plan when solving math problems. Incorporate these math strategies into any math program and use them with a variety of math concepts, from whole numbers and fractions to algebra.
Teaching students how to choose and implement problem-solving strategies helps them develop mathematical reasoning skills and critical thinking they can apply to real-life problem-solving.
READ MORE : 8 Common Core math examples
There are many different strategies for problem-solving; Here are 5 problem-solving strategies: • draw a model • act it out • work backwards • write a number sentence • use a formula
Here are 10 strategies of problem-solving: • Read the problem aloud • Highlight keywords • Summarize the information • Determine the unknown • Make a plan • Draw a model • Act it out • Work backwards • Write a number sentence • Use a formula
1. Understand the problem 2. Devise a plan 3. Carry out the plan 4. Look back
Some strategies you can use to solve challenging math problems are: breaking the problem into smaller parts, using diagrams or models, applying logical reasoning, and trying different approaches.
Related articles

Why Student Centered Learning Is Important: A Guide For Educators

13 Effective Learning Strategies: A Guide to Using them in your Math Classroom

Differentiated Instruction: 9 Differentiated Curriculum And Instruction Strategies For Teachers

5 Math Mastery Strategies To Incorporate Into Your 4th and 5th Grade Classrooms
Ultimate Guide to Metacognition [FREE]
Looking for a summary on metacognition in relation to math teaching and learning?
Check out this guide featuring practical examples, tips and strategies to successfully embed metacognition across your school to accelerate math growth.
Privacy Overview

Improving Student’s Critical Thinking Skills in Mathematics Education: A Systematic Literature Review
- Riska Novia Sari Universitas Pendidikan Indonesia
- Dadang Juandi
Improving students' critical thinking skills is the goal of 21st-century learning. Therefore, this Systematic Literature Review (SLR) aims to find the techniques for improving students' critical thinking skills, especially in mathematics education. Data collection was obtained from scopus database. 24 publications published between the years 2018 to 2022 were retrieved for further analysis. Various tools were employed, they are; Microsoft excel and VostViewer. The result of the analysis showed that the techniques used to improve critical thinking skills include teaching methods, teaching materials, robotic coding activities, teacher attitudes, and the Olympics. The teaching method mostly used to improve critical thinking in mathematics education which is popularly used is Problem Based Learning (PBL) and Science Technology Engineering Mathematics (STEM) approach. This literature review is intended to help educators better understand learning tools to enhance students' critical thinking skills. This can make the mathematics learning process more creative and meaningful.

- Endnote/Zotero/Mendeley (RIS)
Copyright (c) 2023 Riska Novia Sari, Dadang Juandi

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License .

- For Readers
- For Authors
- For Librarians

Critical thinking definition

Critical thinking, as described by Oxford Languages, is the objective analysis and evaluation of an issue in order to form a judgement.
Active and skillful approach, evaluation, assessment, synthesis, and/or evaluation of information obtained from, or made by, observation, knowledge, reflection, acumen or conversation, as a guide to belief and action, requires the critical thinking process, which is why it's often used in education and academics.
Some even may view it as a backbone of modern thought.
However, it's a skill, and skills must be trained and encouraged to be used at its full potential.
People turn up to various approaches in improving their critical thinking, like:
- Developing technical and problem-solving skills
- Engaging in more active listening
- Actively questioning their assumptions and beliefs
- Seeking out more diversity of thought
- Opening up their curiosity in an intellectual way etc.
Is critical thinking useful in writing?
Critical thinking can help in planning your paper and making it more concise, but it's not obvious at first. We carefully pinpointed some the questions you should ask yourself when boosting critical thinking in writing:
- What information should be included?
- Which information resources should the author look to?
- What degree of technical knowledge should the report assume its audience has?
- What is the most effective way to show information?
- How should the report be organized?
- How should it be designed?
- What tone and level of language difficulty should the document have?
Usage of critical thinking comes down not only to the outline of your paper, it also begs the question: How can we use critical thinking solving problems in our writing's topic?
Let's say, you have a Powerpoint on how critical thinking can reduce poverty in the United States. You'll primarily have to define critical thinking for the viewers, as well as use a lot of critical thinking questions and synonyms to get them to be familiar with your methods and start the thinking process behind it.
Are there any services that can help me use more critical thinking?
We understand that it's difficult to learn how to use critical thinking more effectively in just one article, but our service is here to help.
We are a team specializing in writing essays and other assignments for college students and all other types of customers who need a helping hand in its making. We cover a great range of topics, offer perfect quality work, always deliver on time and aim to leave our customers completely satisfied with what they ordered.
The ordering process is fully online, and it goes as follows:
- Select the topic and the deadline of your essay.
- Provide us with any details, requirements, statements that should be emphasized or particular parts of the essay writing process you struggle with.
- Leave the email address, where your completed order will be sent to.
- Select your prefered payment type, sit back and relax!
With lots of experience on the market, professionally degreed essay writers , online 24/7 customer support and incredibly low prices, you won't find a service offering a better deal than ours.
Critical Thinking in Mathematics Education
- Reference work entry
- First Online: 01 January 2014
- Cite this reference work entry

- Eva Jablonka 2
841 Accesses
2 Citations
16 Altmetric
Characteristics
Educational psychologists frame critical thinking (CT) as a set of generic thinking and reasoning skills, including a disposition for using them, as well as a commitment to using the outcomes of CT as a basis for decision-making and problem solving. In such descriptions, CT is established as a general standard for making judgments and decisions. Some descriptions of CT activities and skills include a sense for fairness and the assessment of practical consequences of decisions as characteristics of CT (e.g., Paul and Elder 2001 ). This assumes autonomous subjects who share a common frame of reference for representation of facts and ideas, for their communication, as well as for appropriate (morally “good”) action. Important is also the difference as to what extent a critical examination of the criteria for CT is included in the definition: If education for CT is conceptualized as instilling a belief in a more or less fixed and shared system of skills and criteria for...
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
- Available as PDF
- Read on any device
- Instant download
- Own it forever
- Available as EPUB and PDF
- Durable hardcover edition
- Dispatched in 3 to 5 business days
- Free shipping worldwide - see info
Tax calculation will be finalised at checkout
Purchases are for personal use only
Institutional subscriptions
Appelbaum P, Davila E (2009) Math education and social justice: gatekeepers, politics and teacher agency. In: Ernest P, Greer B, Sriraman B (eds) Critical issues in mathematics education. Information Age, Charlotte, pp 375–394
Google Scholar
Applebaum M, Leikin R (2007) Looking back at the beginning: critical thinking in solving unrealistic problems. Mont Math Enthus 4(2):258–265
Bacon F (1605) Of the proficience and advancement of learning, divine and human. Second Book (transcribed from the 1893 Cassell & Company edition by David Price. Available at: http://www.gutenberg.org/dirs/etext04/adlr10h.htm
Common Core State Standards Initiative (2010) Mathematics standards. http://www.corestandards.org/Math . Accessed 20 July 2013
Ernest P (2010) The scope and limits of critical mathematics education. In: Alrø H, Ravn O, Valero P (eds) Critical mathematics education: past, present and future. Sense Publishers, Rotterdam, pp 65–87
Fawcett HP (1938) The nature of proof. Bureau of Publications, Columbia, New York City. University (Re-printed by the National Council of Teachers of Mathematics in 1995)
Fenner P (1994) Spiritual inquiry in Buddhism. ReVision 17(2):13–24
Fish M, Persaud A (2012) (Re)presenting critical mathematical thinking through sociopolitical narratives as mathematics texts. In: Hickman H, Porfilio BJ (eds) The new politics of the textbook. Sense Publishers, Rotterdam, pp 89–110
Chapter Google Scholar
Garfield JL (1990) Epoche and śūnyatā: skepticism east and west. Philos East West 40(3):285–307
Article Google Scholar
Jablonka E (1997) What makes a model effective and useful (or not)? In: Blum W, Huntley I, Houston SK, Neill N (eds) Teaching and learning mathematical modelling: innovation, investigation and applications. Albion Publishing, Chichester, pp 39–50
Keitel C, Kotzmann E, Skovsmose O (1993) Beyond the tunnel vision: analyzing the relationship between mathematics, society and technology. In: Keitel C, Ruthven K (eds) Learning from computers: mathematics education and technology. Springer, New York, pp 243–279
Legrand M (2001) Scientific debate in mathematics courses. In: Holton D (ed) The teaching and learning of mathematics at university level: an ICMI study. Kluwer, Dordrect, pp 127–137
National Council of Teachers of Mathematics (NCTM) (1989) Curriculum and evaluation standards for school mathematics. National Council of Teachers of Mathematics (NCTM), Reston
O’Daffer PG, Thomquist B (1993) Critical thinking, mathematical reasoning, and proof. In: Wilson PS (ed) Research ideas for the classroom: high school mathematics. MacMillan/National Council of Teachers of Mathematics, New York, pp 31–40
Paul R, Elder L (2001) The miniature guide to critical thinking concepts and tools. Foundation for Critical Thinking Press, Dillon Beach
Pimm D (1990) Mathematical versus political awareness: some political dangers inherent in the teaching of mathematics. In: Noss R, Brown A, Dowling P, Drake P, Harris M, Hoyles C et al (eds) Political dimensions of mathematics education: action and critique. Institute of Education, University of London, London
Skovsmose O (1989) Models and reflective knowledge. Zentralblatt für Didaktik der Mathematik 89(1):3–8
Stallman J (2003) John Dewey’s new humanism and liberal education for the 21st century. Educ Cult 20(2):18–22
Steiner H-G (1988) Theory of mathematics education and implications for scholarship. In: Steiner H-G, Vermandel A (eds) Foundations and methodology of the discipline mathematics education, didactics of mathematics. In: Proceedings of the second tme conference, Bielefeld-Antwerpen, pp 5–20
Walkerdine V (1988) The mastery of reason: cognitive development and the production of rationality. Routledge, London
Walshaw M (2003) Democratic education under scrutiny: connections between mathematics education and feminist political discourses. Philos Math Educ J 17. http://people.exeter.ac.uk/PErnest/pome17/contents.htm
Download references
Author information
Authors and affiliations.
Department of Education and Professional Studies, King’s College London, Waterloo Bridge Wing Franklin-Wilkins Building, SE1 9NH, London, UK
Eva Jablonka
You can also search for this author in PubMed Google Scholar
Corresponding author
Correspondence to Eva Jablonka .
Editor information
Editors and affiliations.
Department of Education, Centre for Mathematics Education, London South Bank University, London, UK
Stephen Lerman
Rights and permissions
Reprints and permissions
Copyright information
© 2014 Springer Science+Business Media Dordrecht
About this entry
Cite this entry.
Jablonka, E. (2014). Critical Thinking in Mathematics Education. In: Lerman, S. (eds) Encyclopedia of Mathematics Education. Springer, Dordrecht. https://doi.org/10.1007/978-94-007-4978-8_35
Download citation
DOI : https://doi.org/10.1007/978-94-007-4978-8_35
Published : 31 July 2014
Publisher Name : Springer, Dordrecht
Print ISBN : 978-94-007-4977-1
Online ISBN : 978-94-007-4978-8
eBook Packages : Humanities, Social Sciences and Law
Share this entry
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Publish with us
Policies and ethics
- Find a journal
- Track your research
share this!
May 21, 2024
This article has been reviewed according to Science X's editorial process and policies . Editors have highlighted the following attributes while ensuring the content's credibility:
fact-checked
trusted source
The case for 'math-ish' thinking
by Stanford University

For everyone whose relationship with mathematics is distant or broken, Jo Boaler, a professor at Stanford Graduate School of Education (GSE), has ideas for repairing it. She particularly wants young people to feel comfortable with numbers from the start—to approach the subject with playfulness and curiosity, not anxiety or dread.
"Most people have only ever experienced what I call narrow mathematics—a set of procedures they need to follow, at speed," Boaler says. "Mathematics should be flexible, conceptual, a place where we play with ideas and make connections. If we open it up and invite more creativity, more diverse thinking, we can completely transform the experience."
Boaler, the Nomellini and Olivier Professor of Education at the GSE, is the co-founder and faculty director of Youcubed, a Stanford research center that provides resources for math learning that has reached more than 230 million students in over 140 countries. In 2013 Boaler, a former high school math teacher, produced How to Learn Math, the first massive open online course (MOOC) on mathematics education . She leads workshops and leadership summits for teachers and administrators, and her online courses have been taken by over a million users.
In her new book, " Math-ish: Finding Creativity, Diversity, and Meaning in Mathematics ," Boaler argues for a broad, inclusive approach to math education, offering strategies and activities for learners at any age. We spoke with her about why creativity is an important part of mathematics, the impact of representing numbers visually and physically, and how what she calls "ishing" a math problem can help students make better sense of the answer.
What do you mean by 'math-ish' thinking?
It's a way of thinking about numbers in the real world, which are usually imprecise estimates. If someone asks how old you are, how warm it is outside, how long it takes to drive to the airport—these are generally answered with what I call "ish" numbers, and that's very different from the way we use and learn numbers in school.
In the book I share an example of a multiple-choice question from a nationwide exam where students are asked to estimate the sum of two fractions: 12/13 + 7/8. They're given four choices for the closest answer: 1, 2, 19, or 21. Each of the fractions in the question is very close to 1, so the answer would be 2—but the most common answer 13-year-olds gave was 19. The second most common was 21.
I'm not surprised, because when students learn fractions, they often don't learn to think conceptually or to consider the relationship between the numerator or denominator. They learn rules about creating common denominators and adding or subtracting the numerators, without making sense of the fraction as a whole. But stepping back and judging whether a calculation is reasonable might be the most valuable mathematical skill a person can develop.
But don't you also risk sending the message that mathematical precision isn't important?
I'm not saying precision isn't important. What I'm suggesting is that we ask students to estimate before they calculate, so when they come up with a precise answer, they'll have a real sense for whether it makes sense. This also helps students learn how to move between big-picture and focused thinking, which are two different but equally important modes of reasoning.
Some people ask me, "Isn't 'ishing' just estimating?" It is, but when we ask students to estimate, they often groan, thinking it's yet another mathematical method. But when we ask them to "ish" a number, they're more willing to offer their thinking.
Ishing helps students develop a sense for numbers and shapes. It can help soften the sharp edges in mathematics, making it easier for kids to jump in and engage. It can buffer students against the dangers of perfectionism, which we know can be a damaging mindset. I think we all need a little more ish in our lives.
You also argue that mathematics should be taught in more visual ways. What do you mean by that?
For most people, mathematics is an almost entirely symbolic, numerical experience. Any visuals are usually sterile images in a textbook, showing bisecting angles, or circles divided into slices. But the way we function in life is by developing models of things in our minds. Take a stapler: Knowing what it looks like, what it feels and sounds like, how to interact with it, how it changes things—all of that contributes to our understanding of how it works.
There's an activity we do with middle-school students where we show them an image of a 4 x 4 x 4 cm cube made up of smaller 1 cm cubes, like a Rubik's Cube. The larger cube is dipped into a can of blue paint, and we ask the students, if they could take apart the little cubes, how many sides would be painted blue? Sometimes we give the students sugar cubes and have them physically build a larger 4 x 4 x 4 cube. This is an activity that leads into algebraic thinking.
Some years back we were interviewing students a year after they'd done that activity in our summer camp and asked what had stayed with them. One student said, "I'm in geometry class now, and I still remember that sugar cube, what it looked like and felt like." His class had been asked to estimate the volume of their shoes, and he said he'd imagined his shoes filled with 1 cm sugar cubes in order to solve that question. He had built a mental model of a cube.
When we learn about cubes, most of us don't get to see and manipulate them. When we learn about square roots, we don't take squares and look at their diagonals. We just manipulate numbers.
I wonder if people consider the physical representations more appropriate for younger kids.
That's the thing—elementary school teachers are amazing at giving kids those experiences, but it dies out in middle school, and by high school it's all symbolic. There's a myth that there's a hierarchy of sophistication where you start out with visual and physical representations and then build up to the symbolic. But so much of high-level mathematical work now is visual. Here in Silicon Valley, if you look at Tesla engineers, they're drawing, they're sketching, they're building models, and nobody says that's elementary mathematics.
There's an example in the book where you've asked students how they would calculate 38 x 5 in their heads, and they come up with several different ways of arriving at the same answer. The creativity is fascinating, but wouldn't it be easier to teach students one standard method?
That narrow, rigid version of mathematics where there's only one right approach is what most students experience, and it's a big part of why people have such math trauma. It keeps them from realizing the full range and power of mathematics. When you only have students blindly memorizing math facts, they're not developing number sense.
They don't learn how to use numbers flexibly in different situations. It also makes students who think differently believe there's something wrong with them.
When we open mathematics to acknowledge the different ways a concept or problem can be viewed, we also open the subject to many more students. Mathematical diversity, to me, is a concept that includes both the value of diversity in people and the diverse ways we can see and learn mathematics.
When we bring those forms of diversity together, it's powerful. If we want to value different ways of thinking and problem-solving in the world, we need to embrace mathematical diversity.
Provided by Stanford University
Explore further
Feedback to editors

New method could allow multi-robot teams to autonomously and reliably explore other planets
2 hours ago

Virgin Galactic completes final spaceflight before two-year pause
6 hours ago

Study finds fresh water and key conditions for life appeared on Earth a half-billion years earlier than thought
21 hours ago

Saturday Citations: Praising dogs; the evolution of brown fat; how SSRIs relieve depression. Plus: Boeing's Starliner
Jun 8, 2024
Nonreciprocal quantum batteries exhibit remarkable capacities and efficiency

New method optimizes lithium extraction from seawater and groundwater

Rare 7-foot fish washed ashore on Oregon's coast garners worldwide attention
Jun 7, 2024

California wildfire pollution killed 52,000 in a decade: study

Quantum chemistry and simulation help characterize coordination complex of elusive element 61

A protein that enables smell in ants—and stops cell death
Relevant physicsforums posts, can i still become a software engineer with this cv.
5 hours ago
Views On Complex Numbers
15 hours ago
Question about branch of logarithm
May 28, 2024
Memorizing trigonometric identities
May 26, 2024
Graphing trip efficiency - distance over time
May 20, 2024
Help with Recurrence Equation
May 18, 2024
More from General Math
Related Stories

Changing students' attitudes to mathematics improves test scores
May 10, 2018

Math degrees are becoming less accessible—and this is a problem for business, government and innovation
May 5, 2024
Former math teacher explains why some students are 'good' at math and others lag behind
Nov 3, 2022

Studies recommend increased research into achievement, engagement to raise student math scores
Feb 15, 2024

5 tips to get your children excited about math
Jan 17, 2020

Future teachers often think memorization is the best way to teach math and science – until they learn a different way
Sep 17, 2020
Recommended for you

How can we make good decisions by observing others? A videogame and computational model have the answer
Jun 4, 2024

Data scientists aim to improve humanitarian support for displaced populations
Jun 3, 2024

A surprising result for a group's optimal path to cooperation
May 30, 2024

Math discovery provides new method to study cell activity, aging

First-generation medical students face unique challenges and need more targeted support, say researchers
May 16, 2024

Mechanistic model shows how much gossip is needed to foster social cooperation
May 15, 2024
Let us know if there is a problem with our content
Use this form if you have come across a typo, inaccuracy or would like to send an edit request for the content on this page. For general inquiries, please use our contact form . For general feedback, use the public comments section below (please adhere to guidelines ).
Please select the most appropriate category to facilitate processing of your request
Thank you for taking time to provide your feedback to the editors.
Your feedback is important to us. However, we do not guarantee individual replies due to the high volume of messages.
E-mail the story
Your email address is used only to let the recipient know who sent the email. Neither your address nor the recipient's address will be used for any other purpose. The information you enter will appear in your e-mail message and is not retained by Phys.org in any form.
Newsletter sign up
Get weekly and/or daily updates delivered to your inbox. You can unsubscribe at any time and we'll never share your details to third parties.
More information Privacy policy
Donate and enjoy an ad-free experience
We keep our content available to everyone. Consider supporting Science X's mission by getting a premium account.
E-mail newsletter
Implementation of PjBL learning model combined with genetics project guidebook II to improve biology students' critical thinking skills
- Agustin, Maya
- Buroidah, Hikmah
- Hayuana, Wachidah
- Fahmi, M. Iqbal Najib
- Maghfiroh, Hidayati
- Choirunisa', Nindiana
- Zubaidah, Siti
- Mahanal, Susriyati
- Sulisetijonov, Sulisetijono
Critical thinking is an intellectually disciplined process of actively and skillfully conceptualising, applying, analysing, synthesising, and evaluating information generated through observation, experience, reflection, reasoning, or communication as a guide for action. Critical thinking allows individuals to solve and observe problems from different perspectives. In the Genetics II course, students must actively find the main concepts of the material through observation, experimentation, making pictures, graphs, and tables, and communicating the results to others. This process is closely related to critical thinking skills. Therefore, applying the PjBL learning model combined with the project guidebook can empower critical thinking in the Genetics II course. This study aims to determine the effect of applying the PjBL learning model combined with the project guidebook on the critical thinking skills of Biology students of the State University of Malang. The research used a pretest-posttest non-equivalent control group design involving 52 students taking the Genetics II course from April-Mei. Data on critical thinking skills were collected using eight essay questions. ANCOVA analysis was performed at a significance level of 0.5% to test the hypothesis. The results of data analysis obtained a significance value of 0.000, which means that there is an effect of the application of the PjBL learning model combined with the project guidebook on the critical thinking skills of biology students. The results showed a significant difference in students' critical thinking skills between learning that started with PjBL combined with a guidebook and PjBL only. Furthermore, the experimental class reached the highest corrected average (PjBL+guidebook), 73.423, while the control class had a corrected average of 65.053. The presence of the project guidebook is intended to support the interaction process between students, lecturers, and lecturer assistants.
- BIOLOGY EDUCATION
Accessibility Links
- Skip to content
- Skip to search IOPscience
- Skip to Journals list
- Accessibility help
- Accessibility Help
Click here to close this panel.
Purpose-led Publishing is a coalition of three not-for-profit publishers in the field of physical sciences: AIP Publishing, the American Physical Society and IOP Publishing.
Together, as publishers that will always put purpose above profit, we have defined a set of industry standards that underpin high-quality, ethical scholarly communications.
We are proudly declaring that science is our only shareholder.
Android-based math learning to improve critical thinking
A Widiyatmoko 1 , S Utaminingsih 2 and Santoso 2
Published under licence by IOP Publishing Ltd Journal of Physics: Conference Series , Volume 1823 , Second UPY International Conference on Applied Science and Education (2nd UPINCASE) 2020 3-4 November 2020, Yogyakarta, Indonesia Citation A Widiyatmoko et al 2021 J. Phys.: Conf. Ser. 1823 012091 DOI 10.1088/1742-6596/1823/1/012091
Article metrics
506 Total downloads
Share this article
Author e-mails.
Author affiliations
1 Student at Post-Graduate of Primary Teacher Education Universitas Muria Kudus, Indonesia
2 Lecturer at Post-Graduate of Primary Teacher Education Universitas Muria Kudus, Indonesia
Buy this article in print
This research aims to describe and the test of effectiveness of android-based integer learning through Smart Apps Creator (SAC) to improve the critical thinking skills at elementary school students. The method research is research and development. The development procedure is adapted from Borg & Gall using ten stages starting from research and information collecting, planning, develop preliminary form of product, preliminary field testing, main product revision, main field testing, operasional product revision, operational field testing, final product revision, dissemination and implementation. Product validation is performed by material, media, and practitioner validators. Research data is obtained from questionnaires, test, observations, and documentation of five elementary schools in Kudus. Analysis of research data uses T-test to determine effectiveness. The results were matched between classes treated using android-based media and SAC with comparison classes that were not treated using android-based media with SAC. The result of T-test in control and experiment class=4,457 trought the degrees significant 0,000<α=0.05. The study results of the experiment group were higher than the control group. Therefore, android-based integer learning with smartapps creator is effective for improving the critical thinking skills of elementary school students.
Export citation and abstract BibTeX RIS
Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence . Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.

IMAGES
VIDEO
COMMENTS
Mathematics provides a systematic and logical framework for problem-solving and critical thinking. The study of math helps to develop analytical skills, logical reasoning, and problem-solving abilities that can be applied to many areas of life.By using critical thinking skills to solve math problems, we can develop a deeper understanding of concepts, enhance our problem-solving skills, and ...
Critical thinking is more than just a buzzword… It's an essential skill that helps students develop problem-solving abilities and make logical connections between different concepts. By encouraging critical thinking in math, students learn to approach problems more thoughtfully, they learn to analyze and evaluate math concepts, identify patterns and relationships, and explore different ...
Using mathematical inversion to improve critical thinking. What's more, the more times we encounter information, the more we believe it, and even when we practice being sceptical, our brains ...
The other problem where performance was unrelated to training, the Petrol Station problem, cannot be characterised similarly. It is more of a logical/critical thinking type problem, where there remains some suggestion that training may have impacted performance, as the Academic group seemed to perform better than the rest of the sample.
This helps them see math as a tool to navigate real-world challenges, thereby promoting critical thinking. 4. What are the six basic steps of the problem-solving process in math? The six steps are: Identification, Analysis, Generation of Alternatives, Decision Making, Implementation, and Evaluation.
Join us for an enlightening conversation with Dr. Igor Subbotin, an esteemed mathematician and educator, as we explore the essential role mathematics plays in our world. Throughout our discussion, we uncover the profound impact that mathematics has on developing critical thinking and problem-solving skills, vital for the 21st-century landscape.
When teaching mathematics, critical thinking skills can be used, practiced and enhanced by effective cognitive methods. Critical thinking can enhance creative problem solving options by encouraging students to seek new ... improve their critical thinking skill levels in this area (Pascarella & Terenzini, 1991). The work of Reichenbach
Logical thinking may be promoted by mathematics, but it is a gradual and complex learning process. Psychological insight into learning, such as that offered by Wason's puzzle, can give students ...
5 Ways to Get Your Students to Think. 1. Answer questions with a refocus on the students' point of view. Liljedahl found in his research that students ask three types of questions: " (1) proximity questions—asked when the teacher is close; (2) stop thinking questions—most often of the form 'is this right' or 'will this be on the ...
content in order for students to understand critical-thinking methods and develop the skills needed to apply them. 5. Demonstrating and encouraging transfer While individual components of critical thinking might manifest themselves differently across subjects, on the whole critical-thinking skills transfer fluidly between domains.
The mathematics curriculum in Australia provides teachers with the perfect opportunity to teach mathematics through critical and creative thinking. In fact, it's mandated. Consider the core processes of the curriculum. The Australian Curriculum (ACARA, 2017), requires teachers to address four proficiencies: Problem Solving, Reasoning, Fluency ...
Definition. Mainstream educational psychologists view critical thinking (CT) as the strategic use of a set of reasoning skills for developing a form of reflective thinking that ultimately optimizes itself, including a commitment to using its outcomes as a basis for decision-making and problem solving.
Mathematics is often promoted as endowing those who study it with transferable skills such as an ability to think logically and critically or to have improved investigative skills, resourcefulness and creativity in problem solving. However, there is scant evidence to back up such claims. This project tested participants with increasing levels of mathematics training on 11 well-studied rational ...
1 Introduction and background. Critical thinking has been considered a key twenty-first century competence by different frameworks (Voogt and Roblin Citation 2012) and by STEM educators (Jang Citation 2016).An education contributing to the development of twenty-first century competences requires, among other things, a reconsideration of instructional processes and a shift from teaching to know ...
The puzzler game is a game that not only increases critical thinking skills, but it also practices both fact fluency and the order of operations! In the puzzler game, students are given a target number. This happens by rolling a die or dice, but it can also be any chosen number between 1 and 36. For instance, I have randomly chosen the date before.
Therefore, learners' critical thinking about their own mathematics learning process was analyzed by using the self-examination and self-correction sub-skills of the sixth core cognitive critical thinking, self-regulation (Figure 1). The APA consensus' definitions of sub-skills self-examination and self-correction were adapted to analyze ...
A team of experienced math experts carefully created each resource to develop students mental arithmetic, problem solving and critical thinking. Explore the range of problem solving resources for 2nd to 8th grade students. One-on-one tutoring . Third Space Learning offers one-on-one math tutoring to help students improve their math skills ...
On the other hand, critical thinking skills will lead a student in the process of analysis, evaluation and synthesis in solving a mathematical problem. This study attempts to perform an alternative solution with a focus on mathematics learning conditions that is held in the lecture room through mathematical investigation approach.
Improving students' critical thinking skills is the goal of 21st-century learning. Therefore, this Systematic Literature Review (SLR) aims to find the techniques for improving students' critical thinking skills, especially in mathematics education. Data collection was obtained from scopus database. 24 publications published between the years 2018 to 2022 were retrieved for further analysis.
To develop mathematical critical thinking skills, students are expected to have a fighting attitude in solving mathematical problems. This can support learning that is oriented towards students ...
Critical thinking, as described by Oxford Languages, is the objective analysis and evaluation of an issue in order to form a judgement. Active and skillful approach, evaluation, assessment, synthesis, and/or evaluation of information obtained from, or made by, observation, knowledge, reflection, acumen or conversation, as a guide to belief and action, requires the critical thinking process ...
Educational psychologists frame critical thinking (CT) as a set of generic thinking and reasoning skills, including a disposition for using them, as well as a commitment to using the outcomes of CT as a basis for decision-making and problem solving. In such descriptions, CT is established as a general standard for making judgments and decisions.
In the book I share an example of a multiple-choice question from a nationwide exam where students are asked to estimate the sum of two fractions: 12/13 + 7/8. They're given four choices for the ...
Critical thinking is an intellectually disciplined process of actively and skillfully conceptualising, applying, analysing, synthesising, and evaluating information generated through observation, experience, reflection, reasoning, or communication as a guide for action. Critical thinking allows individuals to solve and observe problems from different perspectives. In the Genetics II course ...
Abstract. This research aims to describe and the test of effectiveness of android-based integer learning through Smart Apps Creator (SAC) to improve the critical thinking skills at elementary school students. The method research is research and development. The development procedure is adapted from Borg & Gall using ten stages starting from ...
June 7, 2024. Source: University of Galway. Summary: Researchers have created digital babies to better understand infants' health in their critical first 180 days of life. The team created 360 ...