Proof and Problem Solving
This is a homepage for mat299, proof and problem solving, with dr. gilbert at southern new hampshire university. this course introduces students to the practice of proof-writing in the context of integers and basic operations, divisibility, sets, relations, and functions. the focus of the course is on constructing and defending proofs. students will also learn mathematical typesetting and latex syntax using google colab and mathjax., mat 299 - mathematical proof and problem solving.


Course Timeline and Notebooks
Below is a tentative timeline for our course. It includes preparatory work that should be done prior to each class meeting, a detailed set of notes corresponding to each class meeting, and assignments following each class meeting.
| Class Meeting | Before Class | During Class | After Class |
|---|---|---|---|
| 1 | Review Syllabus | Introduction and What to Expect | HW 1: Intro to Colab and LaTeX |
| 2 | HW 2 | ||
| 3 | |||
| 4 | |||
| 5 | HW 3 | ||
| 6 | |||
| 7 | HW 4 | ||
| 8 | |||
| 9 | Catch-Up Day | ||
| 10 | HW 5 | ||
| 11 | |||
| 12 | HW 6 | ||
| 13 | |||
| 14 | HW 7 | ||
| 15 | |||
| 16 | |||
| 17 | Exam I, Part I | ||
| 18 | Exam I, Part II | ||
| 19 | HW 8 | ||
| 20 | |||
| 21 | HW 9 | ||
| 22 | |||
| 23 | HW 10 | ||
| 24 | |||
| 25 | |||
| 26 | Exam II, Part I | ||
| 27 | Exam II, Part II | ||
| 28+ | Oral Proof Defenses |
Back to Hompage
- Help & FAQ
Problem-solving, proving, and learning: The relationship between problem-solving processes and learning opportunities in the activity of proof construction
- Graduate School of Education, Learning & Teaching
Rutgers, The State University
Research output : Contribution to journal › Article › peer-review
In university mathematics courses, the activity of proof construction can be viewed as a problem-solving task in which the prover is asked to form a logical justification demonstrating that a given statement must be true. The purposes of this paper are to describe some of the different types of reasoning and problem-solving processes used by undergraduates to construct proofs in their university mathematics courses, and to consider the relationship between the reasoning that students use when constructing a proof and what they have the opportunity to learn from their proving experience.
| Original language | American English |
|---|---|
| Pages (from-to) | 351-360 |
| Number of pages | 10 |
| Journal | |
| Volume | 24 |
| Issue number | 3-4 |
| DOIs | |
| State | Published - 2005 |
ASJC Scopus subject areas
- Applied Psychology
- Applied Mathematics
- Problem solving
- Problem-solving processes
Access to Document
- 10.1016/j.jmathb.2005.09.005
Other files and links
- Link to publication in Scopus
- Link to the citations in Scopus
Fingerprint
- Mathematics Medicine & Life Sciences 100%
- Learning Mathematics 70%
- Universities Mathematics 62%
- mathematics Social Sciences 52%
- Reasoning Mathematics 48%
- Relationships Mathematics 46%
- university Social Sciences 35%
- Students Engineering & Materials Science 28%
T1 - Problem-solving, proving, and learning
T2 - The relationship between problem-solving processes and learning opportunities in the activity of proof construction
AU - Weber, Keith
N2 - In university mathematics courses, the activity of proof construction can be viewed as a problem-solving task in which the prover is asked to form a logical justification demonstrating that a given statement must be true. The purposes of this paper are to describe some of the different types of reasoning and problem-solving processes used by undergraduates to construct proofs in their university mathematics courses, and to consider the relationship between the reasoning that students use when constructing a proof and what they have the opportunity to learn from their proving experience.
AB - In university mathematics courses, the activity of proof construction can be viewed as a problem-solving task in which the prover is asked to form a logical justification demonstrating that a given statement must be true. The purposes of this paper are to describe some of the different types of reasoning and problem-solving processes used by undergraduates to construct proofs in their university mathematics courses, and to consider the relationship between the reasoning that students use when constructing a proof and what they have the opportunity to learn from their proving experience.
KW - Learning
KW - Problem solving
KW - Problem-solving processes
KW - Reasoning
UR - http://www.scopus.com/inward/record.url?scp=29444445929&partnerID=8YFLogxK
UR - http://www.scopus.com/inward/citedby.url?scp=29444445929&partnerID=8YFLogxK
U2 - 10.1016/j.jmathb.2005.09.005
DO - 10.1016/j.jmathb.2005.09.005
M3 - Article
SN - 0732-3123
JO - Journal of Mathematical Behavior
JF - Journal of Mathematical Behavior
Undergraduate Students’ Understanding of Proof: Relationships Between Proof Conceptions, Beliefs, and Classroom Experiences with Learning Proof
- Published: 19 May 2015
- Volume 1 , pages 91–134, ( 2015 )
Cite this article

- Despina A. Stylianou 1 ,
- Maria L. Blanton 2 &
- Ourania Rotou 3
6104 Accesses
24 Citations
Explore all metrics
This article presents the results from a study of 535 early undergraduate students at six universities that was designed to describe their views of the meaning of proof and how these views relate to their attitudes and beliefs towards proof and their classroom experiences with learning proof. Results show that early undergraduate students have difficulty with mathematical proof. In particular, the study showed that students’ proof choices were strongly influenced by surface characteristics of the tasks. However, a large number of students appear to appreciate and acknowledge the rigor and central role of deductive proof in mathematics despite the difficulties they may face in producing proofs. Further, the study showed a strong positive relationship between students’ beliefs about the role of proof and themselves as learners of proof, but weak relationship between proof ability and self-reported experiences with learning proof.
Similar content being viewed by others

About the Teaching and Learning of Proof and Proving: Cognitive Issues, Curricular Issues and Beyond

Perceptions on proof and the teaching of proof: a comparison across preservice secondary teachers in Australia, USA and Korea

Student perspectives on proof in linear algebra
Avoid common mistakes on your manuscript.
Arguments that the “essence of mathematics lies in proofs” (Ross 1998 , p. 2) and that “proof is not a thing separable from mathematics…. [but] is an essential component of doing, communicating, and recording mathematics” (Schoenfeld 1994 , p. 76) reinforce the centrality of proof in mathematical thinking. Moreover, not only does the act of proof “distinguish mathematical behavior from scientific behavior in other disciplines” (Dreyfus 1990 , p. 126), it also serves as a tool for learning mathematics (Hanna 1990 , 1995 ; Hersh 1993 ). As such, mathematicians and mathematics educators have called for the learning of proof to become a central goal of mathematics learning and instruction (NCTM 2000 ; RAND Mathematics Study Panel 2003 ). The Committee on the Undergraduate Program in Mathematics, appointed by the Mathematical Association of America (MAA) to identify major issues and develop tentative recommendations for an undergraduate mathematics Curriculum Guide (MAA 2000 ), has emphasized this goal and has recommended that proof should be a part of students’ mathematical experiences—especially of those students in mathematics-related programs. The report states that “students should understand and appreciate the core of mathematical culture: the value and validity of careful reasoning, precise definition and close argument” (p. 6).
Yet, research in mathematics education indicates that most students, in particular at the secondary school level, face substantial difficulties with proof (see Harel and Sowder 2007 ; Stylianou et al. 2009 for reviews). There also is evidence that college students face similar difficulties with proof as their high school counterparts. Most notably, Harel and Sowder ( 1998 ) showed that college students focus their attention on the format of the proof rather than the content. However, we know little about the conceptions of students as they are beginning to immerse themselves in college mathematics. Perhaps more importantly, we have not yet explored the relationship between students’ understanding of proof and their beliefs towards proof. Indeed, we now know that mathematics performance in general, and the reading and writing of proofs in mathematics in particular, is a complex one that depends on a wide expanse of beliefs, knowledge, and cognitive skills and that is uniquely shaped by the realm in which learning occurs (Heinze et al. 2005 ). It is not at all clear, however, which of these beliefs and skills are the most salient for undergraduate students nor how they interact with one another (Moore 1994 ). Consequently, research that examines students’ conceptions of proof in relation to their beliefs and attitudes towards proof, as well as their experiences in learning proof, is greatly needed.
Purpose of the Study
We intend to extend existing research on students’ understanding of proof by describing early undergraduate Footnote 1 students’ views of proof, how these views compare with their beliefs about proof, and relationships between their views of proof and their classroom experiences learning proof. More specifically, the following research questions guided the work presented here:
What types of arguments do early undergraduate students accept as proof Footnote 2 ? That is, are students’ judgments of an argument influenced by its appearance in the form of the mathematical proof and the context in which it is used rather than the correctness of the argument? Do students of different achievement levels in mathematics vary in their ability to choose deductive arguments?
What are early undergraduate students’ beliefs about the nature of proof, about themselves as learners of proof, and about the teaching of proof?
What are early undergraduate students’ classroom experiences with learning proof (as self-reported)?
How do early undergraduate students’ choices of arguments as proofs compare with their beliefs about proof?
Theoretical Background
Perspective on the function of proof in mathematics.
Traditionally, the function of proof has been considered to be that of verification of the correctness of mathematical conjectures. However, as a number of scholars have suggested at various times (e.g., Balacheff 1991 ; Bell 1976 ; DeVilliers 1990 ; Hanna 1990 ; Hersh 1993 ; Lakatos 1976 ), proof has other critical functions in mathematics in addition to verification. In particular, DeVilliers ( 1990 ) proposed that mathematical proof has six interrelated roles: verification, explanation, communication, discovery, systematization, and intellectual challenge. While all six roles are important, our study addressed the first three roles of proof primarily. Footnote 3 In line with Knuth ( 2002a , b ), we found that, while these roles were proposed in regard to the role of proof in the discipline of mathematics, they provide a useful framework for thinking about school mathematics in general, and students’ conceptions of mathematical proof in particular. Below we explicate three of these roles as a framework for our study.
The first role of proof—verification as a means to demonstrate the truth of a mathematical conjecture or an assertion—is the most widely held view of proof (Hanna 1990 ). Indeed, most people who have some understanding of the nature of mathematics as a science expect that for each correct conjecture there is a “sequence of logical transformations moving from hypothesis to conclusion” (DeVilliers 1990 ) whose role is to guarantee the truth of the conjecture in an absolute and definite manner. Although Davis and Hersh ( 1981 ) characterize this as a naïve view of mathematics (as proof can be fallible), formal verifications maintain an important and useful role in mathematics.
Verification, however, is not the only aspect of proof for practicing mathematicians. Often proofs are used as a means to gain further insight into a conjecture, to understand the underlying reasons why the conjecture is true. Of course, not all proofs have equally explanatory power. Hanna ( 1990 ) separates proofs into those that establish certainty and those that explain. Some claim that, in fact, the explanatory role of proof is of greater importance to mathematicians than its verification role (e.g., Hersh 1993 ).
A third role of proof is communication. This refers to the “social interaction about the meaning, validity, and importance of the mathematical knowledge offered by the proof produced” (Harel and Sowder 2007 , p. 817). The emphasis falls on the social process of interaction among individuals while doing mathematics. Lakatos ( 1976 ) has argued that, within the mathematics community, proof is at the center of mathematical discussions that allow an argument to evolve in a dynamical manner. This social interaction also involves the subjective negotiation of not only the meanings of concepts concerned, but implicitly also of the criteria for an acceptable argument. As Hanna ( 1989 ) has said, this social negotiation is very important in the acceptance of a particular result and its proof by mathematicians.
Overall, proof in mathematics is multifaceted and should be viewed as such by learners of mathematics. Indeed, a mature proof conception should include all three functions of proof discussed above, even though previous studies suggest that students view proof only in its first role (verification tool). This multifaceted view of proof leads to the first research question that guided our study, namely, to detail undergraduate students’ conceptions of the various roles of proof and to use these views as a lens for understanding students’ difficulties in proof.
Students’ Beliefs About Proof
One of the goals of the study was to identify students’ beliefs about proof as a subject, about themselves as learners of proof, and about the teaching of proof. Beliefs, attitudes and emotions are used to describe a wide range of affective responses to mathematics (McLeod 1992 ). While all three may impact mathematics learning, it is argued that beliefs about mathematics may reveal students’ deeply held convictions and may play a prominent role in students’ problem-solving behaviors (McLeod 1992 ; Schoenfeld 1992 ). Beliefs are developed gradually over a long time, are influenced by students’ personal experiences, and are influenced by larger cultural factors. Students’ beliefs emerge from personal experience (even personal experience of culture), and, once formed, influence their personal experience by shaping ways they construe contexts in which they operate. Consequently, students’ beliefs both summarize and shape their experience. As Schoenfeld ( 1992 ) noted, “whether acknowledged or not, whether conscious or not, beliefs shape mathematical behavior. Beliefs are extracted from one’s experiences and from the culture in which one is embedded” (p. 360).
McLeod ( 1992 ), in a review of the literature on affective issues, used a variation of the classification of beliefs proposed by Lester et al. ( 1989 ), who described beliefs in terms of the subjective knowledge of students regarding mathematics, beliefs about self as learner of mathematics, and beliefs about mathematics teaching. He concluded that beliefs in the first two of these dimensions play a central role in mathematics learning. Indeed, a brief review of this literature suggests that there is a significant correlation between achievement in mathematics and confidence in doing mathematics, as well as between achievement and perceived motivation and personal control (Fennema and Sherman 1977 ; Lester et al. 1989 ; Reyes 1984 ; Schoenfeld 1989 ). However, McLeod noted a void in the literature on students’ beliefs about mathematics instruction (and, as a result, how beliefs on mathematics instruction may relate to students’ achievement in mathematics)—a void that remains two decades later.
Research on the learning of mathematical proof has not documented students’ beliefs about proof nor their beliefs about their own role in learning proof. Even less is known regarding the possible relationship between these beliefs and students’ achievement in either constructing or evaluating proof. One of our goals in this study was to gain further insights into students’ beliefs with respect to proof in the three dimensions suggested by Lester et al. ( 1989 )—verification, explanation, communication—and the relationship of these beliefs to students’ proof conceptions.
Participants
The participants were 535 undergraduate students from six American universities. The study focused on early undergraduate students—those students who were successful in high school mathematics, hence, enrolled in further, college level mathematics. Participation was voluntary and based on the criteria that participants (1) had not previously taken formal courses in mathematical proof, (2) had not completed any courses beyond an early college mathematics course (first or second semester calculus or equivalent), and (3) were enrolled in a course for which the instructor had agreed to administer data instruments during class instruction. Footnote 4 Most students had not, at the time of the study, declared a major, but were enrolled in mathematics courses that are typical for students who aim to major in mathematics, the sciences, or engineering. Footnote 5 At each university one mathematics professor was asked to oversee the process and ensure that participants satisfied the criteria we set. Once the data were collected, we checked the student-reported data and screened out students who did not satisfy our criteria (for example, data from a group of students who reported being enrolled in a linear algebra course were disregarded).
While it was not possible to randomly select student participants, effort was made to use a variety of educational settings in order to have a sample that could be considered representative with respect to demographics and university type. More specifically, the six data collection sites included large and small public and private universities located in Eastern, Western, and Mid-Western regions of United States. Institutions were selected to represent urban and rural areas and varied with respect to their degree of focus on research. In particular, four of these universities were located on the East Coast, one in the Mid-Western region and one on the West coast. Two of the universities are considered to be research institutions, offering graduate programs in mathematics and the sciences, while the remaining four have a stronger emphasis on teaching at the undergraduate level. One of the six institutions has a strong urban identity with a distinctively diverse student body while one other university has a rural character. The remaining four universities are located in mid-size cities in the US. The six universities also varied with respect to the socio-economic profile of their student bodies: one is a private university, while two others are public universities whose mission is to provide access to students of low socio-economic status and also to students who may be first-generation college graduates, Footnote 6 , Footnote 7
Indeed, statistics (gender, ethnicity, scores on the Scholastic Achievement Test [SAT®]), based on student self-reporting suggest that our sample is representative of the overall college student population of the US. Table 1 , which compares the sample’s representativeness with regards to gender and ethnicity to the overall US college student population (ETS 2003 ), suggests that the demographics for participants in the study are aligned with the overall US college student population.
A subset of 60 students also participated in a written test and an interview. This was a convenience sample; that is, as these students would have to meet with us three times, we invited only those that were geographically accessible to us. The self-reported demographic data, however, suggest that the subset was similar in preparation and demographics to the larger sample of 535 study participants.
Research Instruments
An instrument consisting of (1) a short background demographic questionnaire, (2) a multiple-choice test, (3) a survey questionnaire, (4) a written test, and (5) an interview was designed specifically for the purposes of this study. The first three were administered to the entire sample (as will be explained in the next section), while the last two were only administered to a subset of the study sample.
Background Questionnaire
The first part of the research instrument consisted of questions aiming to provide information regarding the demographics of our study sample. Students were asked to provide information regarding their gender, ethnicity, mathematics aptitude as measured by the Scholastic Achievement Test [SAT®], their general mathematics background (e.g., mathematics classes students completed and grades they received), and their background with respect to proof. This information helped us determine whether our sample was representative of the overall college student population of the US. It was also used for background factors in the data analyses of the multiple-choice part of the instrument.
Multiple-Choice Test
The multiple-choice test was designed to examine students’ views on what comprised a proof, its role and function in mathematics, and students’ competency in evaluating simple mathematical proofs. As such, each item had one correct answer. That is, each item could be scored as correct (1 point) or incorrect (0 points). The test consisted of 38 items that fell in one of two categories:
Items 1–5 elicited students’ views on the overall role (e.g., students’ beliefs on what constitutes proof), meaning, and function of proof.
Items 6–38 examined students’ ability in evaluating simple proofs and elicited their views on the role of these specific proofs. In this case, students were presented with mathematical conjectures and a range of four arguments in support of each of them. Students were asked to select (a) the argument nearest to the approach they would have used had they been asked to produce one, (b) the argument they viewed as most rigorous (mathematically correct), and (c) the argument they would use to convince a peer. They were also asked to assess each argument for its validity, explanatory power and generality. Items 6–14, 15–22, 23–30, and 31–38 corresponded to one of four conjectures respectively, Fig. 1 shows one conjecture Footnote 8 with four supporting arguments and the multiple choice questions asked of students regarding them. The complete instrument is presented in the Appendix .
One mathematical conjecture with four argument choices and corresponding multiple-choice items
The order of the different types of arguments varied among the items. For example, the first argument for the first conjecture was empirical, while the third argument for the second statement was empirical. Similarly, the order of the questions following each conjecture and supporting arguments also varied for each conjecture.
The design of the items was modeled after several studies that examined similar constructs with students of younger levels (e.g., Healy and Hoyles 2000 ), pre-service teachers’ conceptions of proof (e.g., Knuth 2002a , b ; Martin and Harel 1989 ), and undergraduate students’ ability to judge validity of proofs (e.g., Morris 2002 ; Selden and Selden 2003 ). The instrument design followed partly the framework proposed by Balacheff ( 1988 ) and its implementation by Healy and Hoyles ( 2000 ) in that each conjecture was followed by four arguments of specific types:
an argument characterized as empirical (e.g., Argument A in Fig. 1 ),
an argument that relied on common properties presented in a narrative but with insufficient explanation (e.g., Argument B in Fig. 1 ). This argument can, by some standards, be considered deductive,
an argument that could be characterized as a deductive proof written in simple formal style using mathematical symbols (e.g., Argument C in Fig. 1 ), and
a visual argument that relied on common properties of a generic case (e.g., Argument D in Fig. 1 ).
In short, each argument could be classified in two different ways: First with respect to the mode of presentation (i.e., narrative, numeric, visual or symbolic), and, second with respect to the proof schema each represented (i.e., empirical vs. deductive, Footnote 9 as proposed by Balacheff ( 1988 ) and Harel and Sowder ( 1998 )). Note that the instrument included some distractor items in the deductive category. That is, some “deductive-in-appearance” arguments that were nonsensical mathematically were included in the instrument.
The instrument included four mathematical conjectures (shown in Table 9 ) that also varied with respect to mathematical content and level of difficulty. It is important to note that the tasks included in the instrument were ones that first and second-year college students with little exposure to advanced mathematics could understand. Our goal was to make the instrument mathematically accessible to all students in order to maximize students’ levels of response.
Survey Questionnaire
The survey questionnaire was also given to the entire sample—all students who were given the multiple-choice test also completed the survey. It consisted of 45 Likert-Scale questions that aimed to elicit students’ beliefs about proof and their previous classroom experiences with proof, both in college and in high school. The design of the instrument followed common Likert-scale survey methods (e.g., it used varied positive and negative responses that were subsequently reversed, etc.) (Hinkle et al. 1994 ).
To identify students’ beliefs about proof, following the theoretical framework proposed by Lester et al. ( 1989 ) the survey focused on three contexts of proof: (a) beliefs about proof, (b) beliefs about themselves as learners of proof, and (c) students’ previous experiences with proof in instructional settings. Table 10 shows examples of items that were designed to address each of these three contexts of proof. A fourth group of items was developed to address students’ previous experiences with proof. Overall, the survey was designed to:
Identify patterns in student views about mathematical proof and about themselves as learners of proof—enabling us to classify their views in general profiles.
Investigate relationships between students’ profiles (identified through the survey) and students’ proof conceptions (as assessed by the multiple-choice instrument).
Identify patterns in students’ previous experiences with proof (as self-reported).
Written Test
A subset of 60 students were asked to construct proofs for the four conjectures contained in the multiple-choice instrument instead of responding to multiple-choice items themselves. Two weeks later they were also given the multiple-choice instrument and survey.
Pilot Testing and Refining the Research Instrument
The validity and reliability of the instrument was established using a series of psychometric procedures. First, to establish content (face) validity of the multiple-choice instrument, we asked several mathematicians and mathematics educators with experience in the teaching of college mathematics to review the tasks and discuss their appropriateness for the purposes of our study. Further, all parts of the instrument, as well as the written open-format test and the interview procedures, were pilot-tested twice during the two years previous to the study reported here. The pilot instrument was administered to a group of 100 students during the first year at one university and 400 students the subsequent year at all six participating universities. The data from student responses were analyzed each year and each part of the instrument was modified during each phase of pilot testing on the basis of these responses.
Each year we conducted an item analysis (item difficulty and item discrimination). Item difficulty index ( p -value), defined as the proportion of examinees who answered the item correctly, can range from 0 to 1. Items with higher p-values (e.g., p -value = 0.9) are easier than items with lower p-values (e.g., p -value = 0.3). Although, in the final pilot test, p -values for the multiple-choice items indicated a range in level of difficulty (0.12 ≤ p -value ≤ 0.68), overall, p -values were positively skewed suggesting that the test was moderately difficult. In particular, 12 items were considered difficult ( p -value < 0.30) and the remaining 26 items were considered moderately difficult (0.31 < p -value < 0.7).
Item discrimination is an index that indicates the contribution of each item to the total score—a correlation between the item score and the total score. Item discrimination scores can range from −1 to 1. The closer the value of item discrimination to the value 1, the more informative the item is. A discrimination value equal to 0 means that the item does not provide any information and such items should be excluded from subsequent analysis. A negative discrimination index is an indication of poorly developed item and should be excluded from the analysis. Several factors may contribute to the negative or near zero discrimination indices. These include items that are poorly worded (items that are poorly worded and might cause confusion should not be included in the scoring of the test as they may result in misleading findings); items that do not measure the same construct as the remaining items in the test (these items contribute in a lower test reliability (internal consistency) and should be removed from the test); items that are scored in error (the key of the items was checked and no errors in scoring had been made). After the initial pilot-testing phase of the study (see Data Collection and Analysis Procedures) , items with negative or zero discrimination values were dropped from the instrument. Hence, all items used on the final version of the instrument were ones that had a positive discrimination index during the final data collection phase.
Finally, the reliability of the multiple-choice test was computed using the Cronbach alpha formula and was equal to 0.79 ( α = 0.79). Similarly, the reliability of the survey questionnaire was computed and was equal to 0.89.
Data Collection and Analysis Procedures
Data collection.
The short background demographic questionnaire, the multiple-choice test, and the survey questionnaire were administered to 535 students in the six participating universities early in the Fall semester under comparable testing conditions. To minimize order effects, the order in which the multiple-choice test and the survey questionnaire were administered was interchanged: Half the students received the multiple-choice instrument first and the survey questionnaire second, while the remaining participants received the two parts in reverse order.
A subset of the participants was also asked to participate in the written test and a subsequent interview.
Written test: Two weeks prior to taking the multiple-choice test and survey questionnaire described above, 60 students were asked to also construct proofs to four conjectures. All students were administered the written test within a classroom setting and were given sufficient time to respond to the items (students were given 1 hour to complete the test and were offered more time if needed). The 60 students attended an urban and a rural college on the East Coast.
Interview: Of the 60 students who took the written test, 40 participated in interviews. The interviews occurred 2 weeks following the administration of the multiple-choice test. An effort was made to interview students who represented the broader spectrum of participants, both with respect to demographics and with respect to performance on the multiple-choice test. That is, students who received high or low scores on the multiple-choice instrument were encouraged to participate in the interview (all 60 students were invited to do so). The 30-min clinical interview consisted of a set of structured questions to probe the reasons for students’ responses in the written and the multiple-choice instruments. Each interview was tailored to the student in it. The student was asked to discuss possible discrepancies in his responses, the reasons for choices he had made for a particular argument as either “rigorous” or “explanatory”, and why he had assessed a certain argument as logically flawed, etc. Our aim for these interviews was to gain further insight into students’ written and multiple-choice test responses.
Data Analysis
In order to better understand the findings of the study, we applied an integrated approach for analyzing data. Information from the multiple-choice test, background demographic questionnaire, survey questionnaire, written test and interviews were used in an integrated manner in order to identify patterns and better understand the findings of the study. In general, data from the multiple-choice were presented in terms of total test scores, while information collected from the various parts of the questionnaire was presented in the form of percentages.
To analyze the data from the survey questionnaire, students were placed into three groups based on their score on the multiple-choice part of the instrument: (a) high-performing (students who scored 26–38 correct responses), (b) middle-performing (students who scored 14–25), and (c) low-performing (students who scored 1–13). Further, students in each group were classified into four profiles based on their beliefs about proof and their own role in their learning of proof (as in Carlson et al. 1999 ).
The questions we were interested in answering involved frequencies of students in the different groups (e.g. high- and low-performing, or agree and disagree) and how each of these groups compared in their approach to proof. For example, we were interested in examining whether more low- than high-performing students chose a specific approach in producing proof. In other words, were there any patterns between performance level and students’ approach to or perception of producing proof? Hence, one example of a hypothesis is the following: “There was no statistically significant difference between the number of students in the high- and low-performing groups in choosing the deductive-symbolic argument”.
Because the main focus of the hypotheses tested was the comparison of the frequencies between two or more groups, a chi-square test for dependent samples was applied. Data on frequency are not expected to be normally distributed. In such cases, non-parametric tests like the Chi-square test is recommended (Hinkle et al. 1994 ), as Chi-square is a test that is usually applied to compare two or more groups on nominal level variables.
We recognize that the use of inferential statistics is highly problematic for samples that are not selected randomly; a sample that is representative of the population is a vital factor in generalizing and making inferences about the findings of the study. One way of obtaining such samples is by applying random selection approaches. However, in quasi-experimental studies where such an approach is not feasible, alternative ways like stratified methods can be used to obtain a sample that is representative of the population. In the current study, we attempted to recruit sites that represent the overall college population. As stated earlier, an evaluation of the selected student sample showed that the participant sample was aligned with the overall US college student population with respect to demographic variables such as gender and race. Thus, we feel confident that inferences about the findings of the study could be generalized to the population.
Written Test and Interview Data Analysis
Following the analysis of the multiple-choice instrument, we attempted to contextualize the descriptive statistics and the statistical correlates identified in the quantitative analyses through data from the student interviews. In particular, proof constructions of students who were interviewed were coded with respect to proof schemas (i.e., as empirical or deductive) using the Harel and Sowder ( 1998 ) classification, and mode of presentation (i.e., as narrative, symbolic, numeric or visual). These proof constructions were subsequently compared and contrasted with students’ choices on the multiple-choice test using correlation tests. In Fig. 2 we present four examples of student-constructed proofs. The work shown of students A and B represents their attempts to construct a proof for Conjecture I. Student A produced a proof we coded as empirical-numeric, while Student B produced a deductive-symbolic proof. Note that the proof is not complete, but the student displayed a disposition towards reasoning in a deductive manner. The work shown of students C and D represents their attempts to construct a proof for Conjecture II. Student C produced an empirical-numeric proof. Student D produced a deductive-narrative proof—even though he attempted to use symbols, his response was presented primarily in a narrative format. Overall, the data that resulted from the written test and interviews were used in this study as supportive to the main data produced by the multiple-choice and survey instruments.
Student-constructed proofs
We first report our findings with respect to the types of arguments that early undergraduate students accept as proof. We then present students’ beliefs about proof and their recollections of instructional experiences regarding proof.
Students’ Proof Conceptions
Examining students’ conceptions regarding the types of arguments that they may accept as proof was the first goal of the study. In the multiple-choice part of the instrument, students were asked to select arguments nearest to the one they would construct if they were asked to produce one. Table 2 shows the distribution of students’ choices in these items.
Students’ Views on the Types of Arguments That Most Resembled Their Own
The first column of Table 2 shows that students’ choices of arguments that most closely resemble what they would produce for Conjectures I–III using the mode of presentation of the conjecture as a lens to understand students’ choices. Students’ choices were almost evenly split between numeric, symbolic, and narrative arguments. Only a small number of students chose the visual argument. For Conjecture IV (supplementary angles) the visual argument (Choice A) was the most popular one (chosen by 38 % of the students). It is worthwhile to point out that Conjectures I–III were about numeric relationships while Conjecture IV was about a geometric relationship.
When using proof schema as a lens (deductive vs. empirical) a different picture emerges: For conjectures I–III about two thirds of the students consistently reported that they would construct one of the two types of deductive proofs—either narrative-deductive or symbolic-deductive (62, 60 and 60 % for Conjectures I–III respectively). For Conjecture IV, 50 % of the students reported that they would construct one of the two types of deductive proofs.
Connecting Student Responses to Their Mathematical Aptitude
In order to better understand students’ overall responses to the multiple-choice tasks, we used data from the background questionnaire to identify some possible factors that may have impacted their choices of arguments that (as they claimed) most closely resembled their own. In particular, we used students’ self-reported scores on the mathematics part of the Scholastic Achievement Test Footnote 10 [SAT®] and looked for differences among high-performing students (SAT score on the mathematics of 660 or higher) and low-performing students (SAT score lower than 660). The data (shown in Table 2 ) indicated that high-performing students were consistently more likely to choose the “deductive-symbolic” argument than their low-performing counterparts. For example, for Conjecture I, 58 % of the high-performing students chose the deductive-symbolic argument compared to 22 % of the low-performing ones.

Comparing Students’ Proof Constructions with Their Responses to the Multiple-Choice Instrument
Two weeks prior to the administration of the research instrument, a subset of the study participants was asked to construct their own proofs for each of the four conjectures. Hence, we were able to compare students’ actual proof constructions and their self-reports as to which one of the given arguments would be closest to the one they would construct. Students’ own proof constructions were coded with respect to proof schemas (i.e., as empirical or deductive) and with respect to mode of presentation (i.e., as narrative, symbolic, numeric or visual) as shown in Fig. 2 .
Table 3 shows the distribution of types of students’ responses in each item as well as their choices in the multiple-choice instrument. There were some remarkable discrepancies in the similarity of students’ choices in the multiple choice instrument regarding the argument they selected as closest to their own approach and their actual proof constructions for each of the four conjectures. The majority of the students who completed the written test consistently constructed proofs that we classified as “empirical-numeric” (45, 49 and 75 % for Conjectures I–III, respectively) even though the majority of the same students (62, 60 and 60 % for Conjectures I–III, respectively) reported that they would construct either a narrative-deductive or a symbolic-deductive argument. In fact, for Conjecture II, the argument that was the most commonly reported as closest to one’s own approach was the least popular type for students’ own proof construction Footnote 11 : 37 % of the students reported that a deductive-symbolic argument was most like their own, while only 17 % of them actually constructed this type of argument. For all three conjectures the discrepancy between students’ own constructions and their choices was statistically significant ( χ 2 = 52.66, df = 9, p < 0.5; χ 2 = 27.33, df = 9, p < .05; χ 2 = 68.66, df = 9, p < .05 for Conjectures I–III respectively). Further, Table 3 shows that when students attempted to go beyond the empirical-numeric approach, they were more likely to give informal narrative arguments rather than either symbolic or visual arguments.
Our follow-up interviews indicated that students often selected the deductive argument because they viewed it as the best proof, one that matched relatively well their intuitive understanding of the given conjecture, even though they would not be able to construct one on their own. The excerpt from Tyler’s interview illustrates this point:
Um, yeah, the reason why I wrote this was… I knew um what it had to say, I just didn’t know how to say this kind of thing. So, the easier… I took the easy way out and just did uh… some examples to kind of prove my point, rather than… I would have done it like (b) [deductive-symbolic] if I could just formulate my ideas better in my head.
Taken together, the data from students’ responses to the multiple-choice instrument and students’ proof constructions suggest that students are better at choosing a correct mathematical proof than constructing one.
Perceptions on the Role and Function of Proof
A second goal of the study was to examine students’ perceptions on the role of proofs in mathematics as a discipline. Students were asked not only to choose the approach that would most closely resemble their own hypothetical approach, but also to select the arguments they viewed as most rigorous (mathematically correct), and the arguments they viewed as most explanatory. Table 4 shows the distribution of students’ choices in these items.
Regardless of students’ choices of the argument closest to their own approaches, there was a remarkable similarity in students’ responses across the four conjectures when asked to choose the “most rigorous” approach. For each of the four conjectures, over half of the participants were able to identify correctly the deductive-symbolic argument as the most rigorous proof (68, 56, 52 and 58 % for Conjectures I–IV respectively) while less than one-fifth chose either the empirical-numeric or the empirical-visual arguments for any of the four Conjectures.
Furthermore, when asked to choose the most “explanatory” argument, that is, the argument they “would use to explain the problem to one of their peers”, students’ choices for Conjectures I, III and IV were relatively closely aligned with their choices of the arguments that would be close to their own approach. In other words, students most closely identified their own hypothetical proof constructions as arguments that were explanatory and communicable. However, for Conjecture II, students’ choices were evenly distributed among the four given arguments. Even so, it is worth noting that for all four conjectures the majority of the students (at least 75 % of the students for each conjecture) did not choose a deductive argument as explanatory.
The narrative argument was the most frequently chosen by students as the most “explanatory” one for Conjectures I–III. During the follow-up interviews we asked students who selected this argument as the most explanatory specifically for reasons why they did so. Many suggested that they had made this choice because they believe that natural language is more explanatory than symbols. When asked for their reasons for choosing the symbolic-deductive arguments as rigorous the same students suggested that they has made this choice because symbols are more “mathematical”. These are illustrated in the interview excerpts below:
It kind of has more laymen terms in it and um… cause (c) [deductive-symbolic argument] is a good answer but it just has a lot of variables in it. It’s easier to think this way rather… like when I first read it, I didn’t think that an even number has to be divisible by two and so I’ll set one to two times an integer. I just kind of thought of that can be divided by two and has the same common factor, so… more with words… […] the rigorous one would be (c) [the symbolic-deductive argument]. Um, it is more mathematically um based.
[I chose the narrative argument] because it is a simple, straightforward as saying like, all right two plus two is four.
Why did you choose different arguments to be the most rigorous and to be the most explanatory?
Rigorous is more like it is true, whereas explanatory is just showing you it is true.
(a) [narrative] is definitely the one I would use to explain it to somebody. Um cause it’s easier to explain in language than in symbols, like mathematical symbols […] [The symbolic-deductive argument] is more like mathematics, you know, like using equations and… it uses actual mathematics to prove instead of just words.
Responses to other questions in the multiple-choice instrument provided further insight into how the students assessed each type of argument. Four questions following each of the three conjectures asked students to determine whether they considered each of the arguments to be either logically flawed, correct but not rigorous, one that shows that the statement is true for some cases, or a strong mathematical argument. (In Fig. 1 , item 10 shows how the question was posed.) As Table 5 shows, students were aware of the limits of an empirical approach. The majority of the students (56, 51, 52 and 43 % for Conjectures I–IV, respectively) assessed the empirical-numeric argument to be “true for only a few cases”, while only a small subset (12, 15, 14 and 21 % for Conjectures I–IV respectively) assessed empirical-numeric arguments to be “strong mathematical argument(s)”.
At the same time, the majority of the students (64, 59, 52 and 53 % for Conjectures I–IV respectively) assessed the deductive-symbolic argument to be a “strong mathematical argument”. Finally, students’ assessment of the narrative and the visual arguments were fairly uniform across the three conjectures: about 40 % of the students said that the arguments were correct but not rigorous.
A third goal of the study was to identify students’ beliefs about proof as a subject, about themselves as learners of proof, and about the teaching of proof, and the relationship of these beliefs to students’ choices of arguments as proofs. Towards this end we used students’ responses to the survey questionnaire in the research instrument.
Table 6 gives a summary of the percentage of students who agreed with statements regarding students’ beliefs towards mathematical proof in relation to their performance on the multiple-choice part of the instrument. Students were placed in three groups based on their score on the multiple-choice part of the instrument Footnote 12 : (a) high-performing (students who scored 26–38 correct responses), (b) middle-performing (students who scored 14–25), and (c) low-performing (students who scored 1–13). Using these criteria, a total of 36 students (6 %) were categorized as high performing, 248 students (46 %) were categorized as middle-performing, and 249 students (46 %) were categorized as low performing. Footnote 13 For the high- and low-performing groups, we report here the percent of students who indicated agreement and disagreement with each of the statements. “Agreed” reflects the percent of students selecting “agree” or “strongly agree” on each of the statements, and “Disagreed” reflects the percent of students selecting “disagree” or “strongly disagree”.
The data in Table 6 suggest that there is a difference in high- and low-performing students’ beliefs about proof and beliefs about themselves as learners of proof. High-performing students tended to hold more positive beliefs about proof than their low-performing counterparts. For example, four fifths (80 %) of the high-performing students agreed that “constructing proofs is an important part of doing mathematics”, while less than half (48 %) of the low-performing students agreed with the same statement. The difference between these distributions was highly significant for this question ( χ 2 = 5.607, df = 1, p < .05). Similarly, high- and low-performing students differed in their choices for questions 25, 26, and 27, which focused on the centrality of proof in learning mathematics ( χ 2 = 4.001, df = 1, p < .05; χ 2 = 9.434, df = 1, p < .05; χ 2 = 13.340, df = 1, p < .05, respectively).
High-performing students also appeared to be more confident in themselves as learners of proof than low-performing students. For example, 83 % of the high-performing students agreed that “It bothers [them] if an instructor tells [them] just to accept a mathematical statement without explaining why it’s true” (item 34) and 92 % of the same set of students agreed or strongly agreed that “[they] feel better about [their] understanding of mathematics if [they] understand why mathematical theorems are true”. Only 51 and 52 % of the low-performing students agreed with these two statements. The difference between the distributions of students’ choices for the first item (item 34) was highly significant for this question ( χ 2 = 4.271, df = 1, p < .05). Differences in high and low-performing students’ responses for questions 30 and 32, which focused on their positive attitude toward proof, were also significant ( χ 2 = 3.952, df = 1, p < .05; χ 2 = 9.233, df = 1, p < .05 respectively).
There was little difference between the two groups’ beliefs about the teaching of proof. For example, 58 and 60 % of the high-performing and low-performing students, respectively, agreed or strongly agreed that “If a mathematical statement requires proof, I think it is the instructor’s (not students’) responsibility to present this to the class”.
Linking Student Profiles on Beliefs About Proof to Students’ Proof Conceptions
As the first two belief categories (“beliefs about proof” and “beliefs about self as learner of proof”) revealed the most difference between high- and low-performing students, these data were further analyzed to help us gain a better understanding of the differences. Students were classified into profiles based on their beliefs about proof and the learning of proof, and these profiles were associated with students’ scores on the multiple-choice test.
First, students were classified into four different profiles according to their responses in the survey items that addressed their beliefs about proof and their own role in their learning of proof. The profiles were: (1) negative or (2) positive with respect to their beliefs about proof, and (3) passive or (4) active with respect to their perceived role in their own learning of proof. Six items (24–29) were used to characterize positive or negative views about proof, and seven items (30–35 and 40) were used to characterize students’ active or passive stance on their role in their own learning of proof.
Students’ choices in these survey items were quantified by a Likert scale (1: strongly disagree, 2:disagree, 3: neutral, 4: agree, and 5: strongly agree). Students who received a score of 24 or higher (of a possible 30) for their responses to items regarding their beliefs about proof were characterized as holding positive views, while students who received a score of 18 or lower on these items were characterized as holding negative views. Footnote 14 Similarly, students who received a score of 28 or higher (of a possible 35) for their responses to items regarding their perceived role in their own learning of proof were characterized as having an active stance, while students who received a score of 21 or lower on these items were characterized as having a passive stance towards proof. Footnote 15 Each student was characterized as either “positive” or “negative” and as “passive” or “active”.
Once again, we looked at the percentage of students who were classified into each profile in relation to their performance on the multiple-choice part of the instrument. Table 7 gives a summary of these data. In comparing these data, we found that 52 % of the high-performing students held a positive and active stance towards proof and the learning of proof, while only 25 % of the low-performing group held similar views. That is, high-performing students are more likely to hold a positive and active stance towards proof than their low-performing counterparts. The data for the “negative and passive” profile supported this result: 44 % of the low-performing students held a negative and passive stance towards proof, while only 24 % of the high-performing students held this stance.
Students’ Perceived Instructional Experiences in Learning Proof
We used data from the survey questionnaire and the background questionnaire to consider students’ self-reported classroom experiences with proof in relation to their proof conceptions. Table 8 summarizes these data.
Table 8 indicates that students who participated in this study reported to have instructors who did not make proof a central part of their mathematical experience. In particular, only 25 % of students reported that previous classroom experiences emphasized the importance of developing proofs, and only 19 % reported that constructing proofs was a regular part of classroom activity. Indeed, although 49 % of students reported that instructors did prove mathematical claims and theorems they made to the class, this percentage suggests that instructors were likely as not to make assertions without justification. Moreover, students reported that when instructors did provide a proof, most (80 %) presented only one argument. Even then, only 49 % of students agreed that their instructors expected students to understand the proofs presented to them. It is worth noting that 62 % percent of students reported that prior instructors used examples to prove mathematical claims.
When students were asked to describe their own experiences and role in constructing proofs, they consistently noted that their participation was peripheral. Less than one fifth (19 %) of the students reported to have “played a significant role in developing proofs during math class.” This was further corroborated by the fact that only 7 % of these students presented their proofs to the class and less than a fourth (23 %) experienced instruction in which proofs were “constructed through whole-class discussions that [built] on students’ ideas”. Indeed, for the majority of the students (67 %), their “experience is that math class is more about taking notes on the instructor’s lectures than arguing with [their] peers about why mathematical statements might be true or not”. Less than one forth of the students worked either individually (23 %) or in groups (12 %) to construct proofs (Tables 9 and 10 ).
These self-reported experiences were consistent regardless of the performance level of students. That is, there was little difference in student responses based on their designation as high performing or low performing.
Regardless of the types of arguments that students accept as proof as indicated by the multiple-choice portion of the instrument, they reported having similar experiences in their mathematics classes with respect to doing proofs. The same finding applies to groups with different mathematics aptitude: students with either high- or low-aptitude with respect to mathematics ability (as indicated by their self-reported SAT mathematics scores) reported similar instructional experiences.
This paper reports results from a study that examined U.S. undergraduate students’ conceptions of proof. In this section we summarize and discuss the main findings with respect to the four main goals of the study: understanding undergraduate students’ conceptions of proof based on the arguments they accept as proof, their beliefs about proof, their self-reported classroom experiences with proof and how these three issues compare.
What Are Early Undergraduate Students’ Conceptions of Proof?
A majority of students chose the deductive argument from proposed arguments for each of four conjectures as the one that would most likely closely resemble their own (had they been asked to construct one), and they also chose deductive arguments to be the “most rigorous ones” and recognized that empirical arguments were limited (“true for only a few cases”). This finding conflicts with previous work in this area. Previous studies on secondary school students, as well as on some classes of college students, reported students’ strong preference for empirical arguments (with respect to proof schema) and numeric arguments (with respect to mode of presentation). Healy and Hoyles ( 2000 ), for example, showed that secondary school students accept empirical arguments as proofs. Similarly, Martin and Harel ( 1989 ) showed that pre-service elementary teachers have a strong preference for inductive arguments, a result that was more recently affirmed by Morris ( 2002 ).
The finding may be explained, in part, by the difference in age between our study participants and other studies which focused primarily on high school students. It is worth recalling that the instrument intentionally consisted of tasks which required that students know something about the mathematical ideas entailed by a conjecture and by the proposed arguments for it. It is possible that, had the study used a set of tasks requiring higher-level mathematical knowledge, the study participants might have responded differently (e.g., they might have then chosen empirical arguments) and this is an issue that is worth pursuing further. Nonetheless, the fact that students in this study appear to have a better conception of what constitutes an acceptable proof than seen in prior studies is encouraging and provides college mathematics instructors a base on which they can build further instruction on proof. Finally, it is worth investigating whether a possible difference in time and curricular trends between past work and this study: It is possible that students in the past few years may have had greater experience and exposure to mathematical proof so they can, at least, identify a deductive argument. However, at this time this is only a hypothesis; while there have been efforts to make proof a regular part of high school students’ mathematics experience, and national mathematics organizations (e.g., the Mathematical Association of America and the U.S. National Council of Teachers of Mathematics) have been calling for proof to take a more central role in the mathematics curriculum, one might question the fidelity of the implementation of these calls. At this time, there are no actual data to show that this has actually happened and participating students’ reports on their classroom experiences with proof certainly do not suggest that this is the case.
Note that students’ choices as to which argument they might accept as proof varied for each of Conjectures I–IV, making it initially hard for us to discern a clear pattern in students’ proof conceptions. This discrepancy invited us to consider the nature of the four conjectures. For Conjectures I and III, more students chose the argument presented in narrative form, while for Conjecture II, the majority of the students chose the argument presented in symbolic form. One possible explanation for the discrepancy with respect to students’ choices in mode of presentation could be due to the statements of Conjectures I and III in natural language and that of Conjecture II in more symbolic form. In other words, the statement of the problem (whether in natural or symbolic language) might affect how students try to prove it (assuming the respondent has had no formal class that focuses on proof, as was the case with our subjects). Similarly, Conjectures I and III reside in number theory, while Conjecture IV in geometry, where diagrams are a more natural part of arguments. As a result, a higher number of students might have chosen a visual argument for Conjecture IV. Both the way a conjecture is stated and the content topic (i.e., geometry) could be considered surface features, and, as such, might have affected students’ solution choice. Studies on expertise indeed show that novices tend to focus on surface characteristics of tasks such as content topic and mode of presentation (e.g., Chi et al. 1988 ; Schoenfeld 1985 ; Stylianou and Silver 2004 ).
Even though the majority of those students who were also asked to construct their own arguments did not construct valid deductive proofs, the same students still indicated a preference for general arguments. This somewhat conflicting finding suggests that students may understand the essence of deductive mathematical arguments (at least in the case of relatively intuitive conjectures that were used in the instrument for this study) but lack the ability to use the representational system necessary to write symbolic-deductive arguments (Weber and Alcock 2006 , 2009 ). Students’ proofs were well-aligned with findings in earlier studies in that, when asked to produce a proof, students construct empirical-numeric proofs. In broader terms, the discrepancy between the arguments that students actually produced and those they selected as closest to what they would construct on their own is reminiscent of research regarding comprehension versus production (e.g., Clark and Hecht 1983 ). That is, it is often easier to understand a proof than to produce one. The knowledge that early college students appreciate deductive arguments yet lack a rich mathematical representational system to articulate their ideas might lead textbook authors and instructors to make ideas of proof more explicit in curricular materials and instruction.
With respect to students’ conceptions on the function of proof, the results show that students do not perceive deductive arguments as explanatory. Instead, students chose the narrative arguments as the “most explanatory” ones. This finding is similar to the findings of Healy and Hoyles ( 2000 ) for middle school students. In their study, too, students saw as explanatory those arguments that were presented to them in words. Healy and Hoyles suggested that it is possible that students
simultaneously held two different conceptions of proof: those about arguments they considered would receive best mark and those about arguments they would adopt for themselves. In the former category algebraic arguments were popular. In the latter, students preferred arguments that they could evaluate and that they found convincing and explanatory, preferences that excluded algebra (p. 425).
It appears that the four or more years of additional mathematics instruction that the students in our sample received did little to change this double-conception held by middle school students. This finding confirms views expressed earlier in the literature. As Schoenfeld ( 1994 ) suggested, proof in traditional high school and undergraduate instruction is used mostly as a verification tool, and not in a way that creates “personal meaning or explanatory power for students” (p. 75). Hence, many students may perceive proof as a task for the instructor, not as a tool for thinking more deeply about mathematics (Alibert 1988 ). Harel and Sowder ( 1998 ) argued that teachers use “proof methods and implication rules that in many cases are utterly extraneous to what convinces [students]” (p. 237). Moreover, proving a statement for which the proof already exists or is intuitively obvious leads to the perception that proof activity is not a process of discovery (Schoenfeld 1994 ; Wheeler 1990 ) and results in a focus on knowing what, which conceals the value of knowing why .
Finally, our analysis showed that students’ proof conceptions were related to their overall mathematics aptitude and achievement. High-performing students on the SAT were consistently more likely to choose the “deductive-symbolic” argument than were low-performing students. This might indicate that proof cannot be viewed as an isolated competency or as an isolated part of mathematics instruction and curriculum, but one part of the overall mathematical competency.
What Are Undergraduate Students’ Beliefs About Proof?
Overall, high-performing students tended to hold a more positive and active stance with respect to their beliefs about proof than their low-performing counterparts. Hence, our findings resonate with findings on general beliefs about mathematics and general mathematics performance. That is, just as high-performing students tend to hold more positive beliefs about mathematics and about themselves as learners of mathematics (McLeod 1992 ), they also tend to hold more positive beliefs about proof and about themselves as learners of proof than their low-performing counterparts.
Results from our analysis suggest that classrooms with passive learning environments might implicitly reinforce low performance on proof activity in particular and mathematical activity in general. It, therefore, raises the instructional challenge to build classrooms where students can be actively engaged in learning about proof as a way to potentially alter a negative, passive stance towards it. The extent to which classroom environments can facilitate an active, positive stance on proof remains an area for further research.
What Are Students’ (Self-Reported) Classroom Experiences with Learning Proof?
Overall, students who participated in this study report to have experienced little instruction that focuses on proof. It is possible that their perception of the kind of instruction they did receive often marginalized their participation in constructing proofs and did not help them develop the representational systems to build general arguments. The finding that students experience with proof is limited is not surprising; previous studies have shown similar findings. For example, in a relatively broad study involving 62 mathematics and science teachers in 18 high schools in six states, Porter ( 1993 ) found that “on average, no instructional time is allocated to students learning to develop proofs, not even in geometry”. Similarly, the report on the videotape study in the Third International Mathematics and Science Study (TIMSS) noted that “the most striking finding in this review of 90 classes was the rarity of explicit mathematical reasoning in the classes […] almost total absence of explicit mathematical reasoning” (Manaster 1998 , p. 803).
Students’ reports that prior instructors often used examples to prove mathematical claims is also worth noting. This raises the question of whether students’ reliance on empirical arguments (e.g., Knuth et al. 2002 ; Porteous 1986 ) might be a reflection of their instructional experiences as much as cognitive issues in their understanding of proof. It also raises the question regarding when instruction should shift from the use of empirical arguments to helping students learn to develop more general arguments (some research indicates that this can begin as early as the elementary grades—see Kaput et al. ( 2008 ); Stylianou et al. 2009 ).
Overall, these data suggest that, regardless of entry-level college students’ understanding of proof, they report to have had limited classroom experiences with seeing or constructing proofs. Additionally, these experiences were often the presentation of empirical arguments by their instructors, with students playing a passive role in their development. As such, these data bring to light persistent instructional paradigms that remove the learner from actively participating in classroom activity and in which individual learning is valued over collaborative learning. Moreover, these types of classroom experiences could help explain why, even at the college level, students often initially cannot construct general arguments and rely instead on empirical arguments. Even though our data suggest that students do know how to recognize a more appropriate deductive argument, their responses to the survey suggest that they have not had the kinds of instructional experiences that would support their learning how to build general, deductive, rigorous arguments.
Finally, this limited experience with proof appears to be consistent in both high- and low-performing students. Regardless of students’ conceptions of proof as indicated by the multiple-choice portion of the instrument and regardless of their overall mathematics achievement as indicated by the SAT, they reported having similar experiences in their mathematics classes with respect to doing proofs.
This study suggests that there is much work to be done in K-14 education to prepare students to understand and construct proofs. In particular, the results suggest that students have potential to develop general arguments, but lack the representational systems to do this. Moreover, the results reported here suggest that students often are not participants in the process of constructing proof, nor do they typically see non-empirical arguments during instruction. This challenges curriculum and instruction to provide experience and opportunity to help students build the tools necessary for understanding and developing proofs.
We define “early undergraduates” to be students who are in their first or second year in college and have not completed a course beyond second semester calculus and have not taken a formal course on proof.
The term “proof” is often reserved to describe formal and precise arguments given by mathematicians. For example, the Harper Collins Dictionary of Mathematics defines proof as “a sequence of statements each of which is either validly derived from those preceding it or is an axiom or assumption, and the final member of which, the conclusion, is the statement of which the truth is thereby established”. However, here we use a broader definition of proof as an argument that one makes to justify a claim and to convince oneself and others of the claim’s veracity. By this definition, proofs can have varying levels of strength.
While proof can play an important role in the discovery of new mathematics (DeVilliers 1990 ) and can be central to the systematization of results such as theorems and axioms into a broader deductive system, it is highly unlikely that undergraduate students have had opportunities to experience these roles of proof. Earlier studies, e.g., NAEP results (Silver and Kenney 2000 ), have shown that students’ experiences with proof are limited, hence we chose to focus on the most “obvious” roles of verification, explanation and communication that are the most likely to have been part of these students’ experience.
No data were collected regarding the current instruction or instructors of the participating students. The instrument was administered early in the semester, hence the current instructor may not have had a significant impact on the students, and, the students were explicitly asked to report on their previous mathematics education, not experiences in their current class.
The majority of the participants were enrolled in a typical first or second semester calculus course. We did not solicit participation from students enrolled in courses such as calculus or quantitative literacy courses for non-science majoring students.
While we attended to university SES data, we did not collect SES data on individual students.
As the preparation of the students at all participating colleges was comparable (by study design) we chose not to investigate type of university as a source of variation in our results. This would be beyond the scope of this study.
We called these statements “conjectures” rather than “theorems” or “statements” to minimize the possibility that students would tacitly assume that they were offered as true statements. We hoped that they would take each statement as coming from someone who genuinely wondered whether it was true,
A number of researchers in the field have identified the three main types of proof schemas as empirical, inductive and deductive. Some, like Harel and Sowder ( 1998 ) have refined these categorizations by identifying sub-categories. Here, we only use the broad three categories.
The SAT is a measure of the critical thinking skills for academic success in college. It measures skills in three areas: critical reading, math, and writing, and it is typically taken by high school juniors and seniors. Each section of the SAT is scored on a scale of 200–800, with two writing sub-scores for multiple-choice and the essay. For more information visit www.ets.org or www.collegeboard.org
This was with the exception of visual arguments that none of the students used in their own construction of proofs.
We need to re-iterate that as these items elicited students’ personal views or preferences with respect to proof, a “score” only indicates the degree of sophistication with respect to proof conception.
There is a large discrepancy in the number of students in each of the three groups. In particular, there were only 36 high-performing students. While changing the criteria for high-, middle- and low-performing could have provided more balanced numbers, it would also diffuse any differences and response patterns.
A score of 24 or higher indicated that students primarily agreed or strongly agreed on the 6 items that were used to characterize positive or negative beliefs about proof, while a score of 18 or lower indicated that students primarily disagreed or strongly disagreed on these items. Scores of 19 to 23 could indicate mixed and “neutral” beliefs that made it difficult to provide a clear profile for these students.
A score of 28 or higher indicated that students primarily agreed or strongly agreed on the 7 items that were used to characterize students’ active or passive stance on their role in the learning of proof, while a score of 21 or lower indicated that students primarily disagreed or strongly disagreed on the 7 items.
Alibert, D. (1988). Towards new customs in the classroom. For the Learning of Mathematics, 8 (2), 31–35.
Google Scholar
Balacheff, N. (1988). Aspects of proof in pupils’ practice of school mathematics. In D. Pimm (Ed.), Mathematics, teachers and children (pp. 216–230). London: Hodder & Stoughton.
Balacheff, N. (1991). The benefits and limits of social interaction: The case of mathematical proof. In A. Bishop, S. Mellin-Olsen, & J. van Dormolen (Eds.), Mathematical knowledge: Its growth through teaching (pp. 175–192). Dordrecht: Kluwer Academic Publishers.
Bell, A. (1976). A study of pupils’ proof-explanations in mathematical situations. Educational Studies in Mathematics, 7 , 23–40.
Article Google Scholar
Carlson, M., Buskirk, T., & Halloun, I. (1999). Assessing College Students’ Views About Mathematics With the Views About Mathematics Survey . http://sigmaa.maa.org/rume/crume2011/RUME2011_FinalSchedule_files/ContributedReportsShortPapers/Carlson%20Rasmussen_proceedings.pdf
Chi, M. T. H., Glaser, R., & Farr, M. J. (1988). The nature of expertise . Hillsdale: Lawrence Erlbaum.
Clark, E., & Hecht, B. (1983). Comprehension, production, and language acquisition. Annual Review of Psychology, 34 , 325–349.
Committee on the Undergraduate Program in Mathematics. (2000). Curriculum Guide. Mathematical Association of America. http://www.maa.org/news/cupm_text.html
Davis, P. J., & Hersh, R. (1981). The mathematical experience . Boston: Houghton Mifflin.
DeVilliers, M. (1990). The role and function of proof in mathematics. Pythagoras, 24 , 7–24.
Dreyfus, T. (1990). Advanced mathematical thinking. In P. Nesher & J. Kilpatrick (Eds.), Mathematics and cognition: A research synthesis by the International Group for the Psychology of Mathematics Education (pp. 113–134). Great Britain: Cambridge University Press.
Chapter Google Scholar
Educational Testing Services. (2003). Sex, race, ethnicity and the performance on the GRE General Test . Princeton: ETS.
Fennema, E., & Sherman, J. A. (1977). Sex-related differences in mathematics achievement, spatial visualization and affective factor. American Education Research Journal, 14 (1), 51–71.
Hanna, G. (1989). More than formal proof. For the Learning of Mathematics, 9 (1), 20–25.
Hanna, G. (1990). Some pedagogical aspects of proof. Interchange, 21 , 6–13.
Hanna, G. (1995). Challenges to the importance of proof. For the Learning of Mathematics, 1 (3), 42–49.
Harel, G., & Sowder, L. (1998). Students’ proof schemes: Results from an exploratory study. In A. H. Schoenfeld, J. Kaput, & E. Dubinsky (Eds.), Research in college mathematics education III (pp. 234–283). Providence: American Mathematical Society.
Harel, G., & Sowder, L. (2007). Toward a comprehensive perspective on proof. In F. Lester (Ed.), Second handbook of research on mathematics teaching and learning . Greenwich: Information Age Publishing.
Healy, L., & Hoyles, C. (2000). A study of proof conceptions in algebra. Journal for Research in Mathematics Education, 31 , 396–428.
Heinze, A., Reiss, K., & Rudoph, F. (2005). Mathematics achievement and interest in mathematics from a differential perspective. Zentrablatt für Didaktik der Mathematik, 37 (3), 212–220.
Hersh, R. (1993). Proving is convincing and explaining. Educational Studies in Mathematics, 24 , 389–399.
Hinkle, E. D., Wiersma, W., & Jurs, G. S. (1994). Applied statistics for behavioral sciences . Boston: Houghton Mifflin Company.
Kaput, J., Carraher, D., & Blanton, M. (Eds.). (2008). Algebra in the early grades . Mahwah: Lawrence Erlbaum/Taylor & Francis Group.
Knuth, E. (2002a). Teachers’ conceptions of proof in the context of secondary school mathematics. Journal of Mathematics Teacher Education, 5 (1), 61–88.
Knuth, E. (2002b). Secondary school mathematics teachers’ conceptions of proof. Journal for Research in Mathematics Education, 33 (5), 379–405.
Knuth, E., Choppin, J., Slaughter, M., & Sutherland, J. (2002). Mapping the conceptual terrain of middle school students’ competencies in justifying and proving. In D.S. Mewborn, P. Sztajn, D.Y. White, H.G. Weigel, R.L. Bryant, & K. Nooney (Eds.), Proceedings of the 24th Annual Meeting for the Psychology of Mathematics Education - North America, v.4 , (pp. 1693–1700). Athens: Clearinghouse for Science, Mathematics, and Environmental Education.
Lakatos, I. (1976). Proofs and refutations . Cambridge: Cambridge University Press.
Book Google Scholar
Lester, F. K., Garofalo, J., & Kroll, D. L. (1989). Self-confidence, interest, beliefs, and metacognition: Key influences on problem-solving behavior. In D. B. McLeod & V. M. Adams (Eds.), Affect and mathematical problem solving: A new perspective (pp. 75–88). New York: Springer.
Manaster, A. (1998). Some characteristics of eighth grade mathematics classes in the TIMSS videotape study. American Mathematical Monthly, 108 (9), 793–805.
Martin, W. G., & Harel, G. (1989). Proof frames of pre-service elementary teachers. Journal for Research in Mathematics Education, 20 , 41–51.
McLeod, D. B. (1992). Research on affect in mathematics education: A reconceptualization. In Handbook of research on mathematics teaching and learning (pp. 575–596). Reston: National Council of Teachers of Mathematics.
Moore, R. C. (1994). Making the transition to formal proof. Educational Studies in Mathematics, 27 , 249–266.
Morris, A. (2002). Mathematical reasoning: Adults’ ability to make the inductive-deductive distinction. Cognition and Instruction, 20 (1), 79–118.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics . Reston: NCTM.
Porteous, K. (1986). Children’s appreciation of the significance of proof. In Proceedings of the tenth International Conference of the Psychology of Mathematics Education (pp. 392–397). London, England.
Porter, A. (1993). Opportunity to learn. Brief no. 7 . Madison: Center on Organization and Restructuring Schools.
RAND Mathematics Study Panel. (2003). Mathematical proficiency for all students: Toward a strategic research and development program in mathematics education . Santa Monica: RAND.
Reyes, L. (1984). Affective variables and mathematics education. The Elementary School Journal, 84 (5), 558–581.
Ross, K. (1998). Doing and proving: the place of algorithms and proof in school mathematics. American Mathematical Monthly, 3 , 252–255.
Schoenfeld, A. H. (1985). Mathematical problem solving . New York: Academic.
Schoenfeld, A. H. (1989). Explorations of students’ mathematical beliefs and behavior. Journal for Research in Mathematics Education, 20 , 338–355.
Schoenfeld, A. H. (1992). Learning to think mathematically: Problem solving, metacognition and sense making in mathematics. In Handbook of research on mathematics teaching and learning (pp. 334–370). Reston: National Council of Teachers of Mathematics.
Schoenfeld, A. (1994). What do we know about mathematics curricula? Journal of Mathematical Behavior, 13 (1), 55–80.
Selden, A., & Selden, J. (2003). Validations of proofs considered as texts: can undergraduates tell whether an argument proves a theorem? Journal for Research in Mathematics Education, 34 (1), 4–36.
Silver, E. A., & Kenney, P. A. (2000). Results from the seventh mathematics assessment . Reston: National Council of Teachers of Mathematics.
Stylianou, D. A., & Silver, E. A. (2004). The role of visual representations in advanced mathematical problem solving: an examination of expert-novice similarities and differences. Journal of Mathematical Thinking and Learning, 6 (4), 353–387.
Stylianou, D., Blanton, M., & Knuth, E. (2009). Teaching and learning proof across the grades . New York: Routledge - Taylor Francis and National Council of Teachers of Mathematics.
Weber, K., & Alcock, L. (2006). Semantic and syntactic reasoning and proving in advanced mathematics courses. In D. Stylianou, M. Blanton, & E. Knuth (Eds.), The teaching and learning of proof across the K-16 curriculum (pp. 323–338). New York: Routledge.
Weber, K., & Alcock, L. (2009). Proof in advanced mathematics classes: Semantic and syntactic reasoning in the representation system of proof. In D. Stylianou, M. Blanton, & E. Knuth (Eds.), Teaching and learning proof across the grades . New York: Routledge - Taylor Francis and National Council of Teachers of Mathematics.
Wheeler, D. (1990). Aspects of mathematical proof. Interchange, 21 (1), 1–5.
Download references
Acknowledgments
The authors wish to thank their colleagues at the participating universities for making this study possible by facilitating the data collection.
The research reported here was supported in part by the National Science Foundation under Grant # REC- 0337703. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.
Author information
Authors and affiliations.
City College School of Education, The City University of New York, New York, USA
Despina A. Stylianou
TERC, Cambridge, MA, USA
Maria L. Blanton
Educational Testing Service, Princeton, NJ, USA
Ourania Rotou
You can also search for this author in PubMed Google Scholar
Corresponding author
Correspondence to Despina A. Stylianou .
Multiple Choice Questions
For the following, please circle the response that best reflects your thinking.
Proving a theorem in mathematics implies
one may need to check if it applies to all cases
it may still be rejected at a future time
one may be able to find an exception
it will always be true
The relationship among the sides of a right triangle expressed in the Pythagorean Theorem is true because it has been
verified by measuring the sides of many right triangles
proven by a logical argument
shown in a picture of a triangle with squares built on its sides
told to you by your math teacher
Proofs are necessary for
geometric theorems only
algebraic theorems only
all areas of mathematics
various, but not all, areas of mathematics
In order to prove that a statement is false, one should
find all possible cases where the statement is false
show several cases where the statement is false
find one example that shows where the statement is false
draw a picture
It should be sufficient to prove that a statement is false by
finding a number of well-chosen counterexamples that look at different cases
finding a single counterexample of the statement
constructing a formal proof that the statement is not true
a drawing that illustrates the statement
Consider the following problem and the four possible solutions A, B, C and D. Then please answer questions 6–14 with reference to solutions A–D below:
Problem: Prove that the sum of any two even numbers is always an even number
Solution A:
+ = | + = | + = |
+ = | + = | + = |
+ = | + = | + = |
Therefore, the sum of any two even numbers is always even.
Solution B:
Even numbers are numbers that can be divided by 2 . When you add numbers with a common factor, 2 in this case, the answer will have the same common factor.
Solution C:
Suppose a and b are two arbitrary even integers.
Then there exist integers j and k such that a = 2 j and b = 2 k .
Thus, a + b = 2 j + 2 k = 2( j + k ), where j + k is an integer.
It follows that the sum of any two even numbers is always even.
Solution D:
Suppose you have any two even numbers of counters:
Then they can be combined in the following way:
As the picture illustrates, the counters can be divided into pairs with no counter left over. Therefore, the sum of any two even numbers is always even.
From the above possible solutions, which one would be closest to what you would do if you were asked to solve the problem?
Which of the following best reflects the reason you chose that particular solution as the best one?
It looks at a number of cases for different kinds of numbers
It uses symbols and formal mathematical language
It provides a more general argument
It uses a diagram to illustrate the concept
From the above solutions, choose the one that is the most “rigorous” (mathematically correct):
From the above solutions, choose the one you would use to explain the problem to one of your peers:
Look again at “Solution A” and determine which of the following best fits your thinking:
It is logically flawed.
It is a correct argument but it is not a rigorous one.
It only shows that the statement is true for some even numbers.
It is a strong mathematical argument.
Look again at “Solution B” and determine which one of the following best fits your thinking:
Look again at “Solution C” and determine which one of the following best fits your thinking:
It is a correct argument but it is not a rigorous one
13. Look again at “Solution D” and determine which one of the following best fits your thinking:
Suppose it has been proven that the sum of any two even numbers is always even. One of your classmates asks what needs to be done to prove whether the sum of two even numbers, that are also square numbers, is always even. Which of the following best reflects your response?
My classmate doesn’t need to do anything; it has already been proven.
My classmate needs to draw a new picture.
Square numbers are a special case and it requires a different proof.
My classmate should look for a counterexample.
Consider the following problem and the four possible solutions A, B, C and D. Then please answer questions 15–22 with reference to solutions A–D below:
Problem: For any integers a, b, and c, prove that if a divides b with no remainder, then a divides bc with no remainder.
If one integer (call it the first one) divides another integer (the second one) without a remainder, then the first integer must be a factor of the second one. Thus, no matter what other third integer you multiply the second one by, the first integer will still always be a factor of that product. This means that if the first integer divides the second integer, then the first integer must divide the product of the second and third integers too.
Let a, b, and c be integers and suppose that a divides b with no remainder. Then b can be written as a multiple of a . That is, b = ak , where k is an some integer. Thus, ( b)c = (ak)c. It follows that since a is a factor of bc , then a divides bc .
Let a = 3, b = 9 and c = 7 . Then 3 divides 9 and 3 divides 9(7) .
Let a = 5, b = 10 and c = 34. Then 5 divides 10 and 5 divides 10(34) .
Let a = 21, b = 126 and c = 1453. Then 21 divides 126 and 21 divides 126(1453)
Let a = −12, b = 96, and c = −15 . Then − 12 divides 96 and − 12 divides 96(−15).
I randomly selected several different types of integers: high and low, positive and negative, prime and composite. Since I randomly selected and tested a variety of types of integers, and it worked in every case, I know that it will work for all integers. Therefore, if a divides b with no remainder, then a divides bc with no remainder.
As the picture illustrates, the counters can be divided into groups of 3 with no counter left over. Therefore, a divides bc with no remainder.
It looks at a number of cases for different kinds of numbers.
It uses symbols and formal mathematical language.
It provides a more general argument.
It uses a diagram to illustrate the concept.
From the above solutions, choose the one that is the most “rigorous” (mathematically correct)
Look again at “Solution A” and determine which one of the following best fits your thinking:
It only shows that the statement is true for some numbers.
Look again at “Solution D” and determine which one of the following best fits your thinking:
Consider the following problem and the four possible solutions A, B, C and D. Then please answer questions 23–30 with reference to solutions A–D below:
Problem: If the sum of the digits of a three-digit integer is divisible by 3, then the number is also divisible by 3.
Let a be any three-digit integer such that the sum of its digits is divisible by 3. Assuming that its digits are x, y, and z, then a = xyz. Let x + y + z be divisible by 3. Then for xyz one may factor out 3 . Hence, 3 is a factor of xyz , then 3 is a factor of a . Therefore, a is divisible by 3.
Let a be any three-digit integer with digits x, y, and z . By the place value concept, a = 100 x +10y + z. This can be re-written as a = (99 x + x) + (9y + y) + z. By the commutative and associative properties, we get a = (99x + 9y) + (x + y + z) . The expression 99x + 9y is always divisible by 9 , and therefore, also by 3. Since the second expression, x + y + z , is also divisible by 3 , by the “sum property” the number itself is divisible by 3.
Let a = 234. 234 is divisible by 3 and 2 + 3 + 4 = 9 is also divisible by 3.
Let a = 1707. 1707 is divisible by 3 and 1 + 7 + 0 + 7 = 15 is also divisible by 3.
Let a = −891. −981 is divisible by 3 and 8 + 9 + 1 = 18 is also divisible by 3.
Let a = −111. 111 is divisible by 3 and 1 + 1 + 1 = 3 is also divisible by 3.
I randomly selected several different types of integers: high and low, positive and negative, and even and odd. Since I randomly selected and tested a variety of types of integers, and it worked in every case, I know that it will work for all integers. Therefore, if the sum of the digits of an integer is divisible by 3, then the number is also divisible by 3
Solution D:—Diagram
As the diagram shows, if the sum of the digits (in this case 2 + 2 + 2) is divisible by three, the number is also divisible by three.
25. From the above solutions, choose the one that is the most “rigorous” (mathematically correct):
It only shows that the statement is true for some three-digit numbers.
Consider the following problem and the four possible solutions A, B, C and D. Then please answer questions 31–38 with reference to solutions A–D below:
Problem: Prove that the supplements of two congruent angles are congruent.
Suppose ∠x and ∠y have the same measure. Then the diagram shows that the supplements of these two angles, 180°—∠x and 180°—∠y, must also have the same measure. Therefore, the statement is true.
If two angles, say ∠A and ∠B, are congruent, then they have the same measure. Consider their supplements. Since the supplement of ∠A (or ∠B) is obtained by subtracting the measure of ∠A (or ∠B) from 180° and since angles A and B have the same measure, then their supplements must be congruent.
Let ∠A and ∠B be two angles for which ∠A ≅ ∠B. That is, m(∠A) = m(∠B), where m(∠X) is the measure of ∠X. Let ∠C be the supplement of ∠A and ∠D be the supplement of ∠B. Then m(∠A) + m(∠C) = 180° and m(∠B) + m(∠D) = 180°.
Thus, m(∠A) + m(∠C) = m(∠B) + m(∠D). But m(∠A) = m(∠B). Thus, by substitution, m(∠A) + m(∠C) = m(∠A) + m(∠D). Finally, subtracting m(∠A) from both sides of this equation implies m(∠C) = m(∠D). Thus, ∠C ≅ ∠D.
Consider two congruent angles that each measure 50°. Each has a supplementary angle that measures 180° − 50° = 130°. Thus, the two supplementary angles have the same angle measure, which means they are congruent. If there are 2 angles that each measure 75°, then the angles are congruent and each has a supplementary angle that measures 180° − 75° = 105°. Thus, the two supplementary angles have the same angle measure, which means they are congruent. These examples show that no matter what the measures of the congruent angles are, their supplements will also be congruent.
From the above answers, choose the one you would use to explain the problem to one of your peers:
Part I: Circle the number that best reflects how often the following occur based on your experiences in mathematics courses:
|
|
|
|
| |
1. Mathematics instructors I had in the past proved the theorems and mathematical claims they presented to the class. | 1 | 2 | 3 | 4 | 5 |
|
|
|
|
|
|
3. Mathematics instructors I had in the past used diagrams and graphs to prove a theorem or a mathematical claim. | 1 | 2 | 3 | 4 | 5 |
|
|
|
|
|
|
5. In my previous math classes students worked in groups to construct proofs. | 1 | 2 | 3 | 4 | 5 |
|
|
|
|
| |
6. In my previous math classes, students worked individually to construct proofs. | 1 | 2 | 3 | 4 | 5 |
|
|
|
|
|
|
8. | 1 | 2 | 3 | 4 | 5 |
Mathematics instructors I had in the past presented more than one proof for the same theorem. |
|
|
|
|
|
10. | 1 | 2 | 3 | 4 | 5 |
Part II: Circle the number that best reflects your agreement with the following based on your experiences in mathematics courses:
|
|
|
|
| |
11. During previous math classes, students played a significant role in developing proofs during math class. | 1 | 2 | 3 | 4 | 5 |
|
|
|
|
|
|
13. In my past experiences, students played a minor role in the development of a proof during classroom instruction. | 1 | 2 | 3 | 4 | 5 |
|
|
|
|
|
|
15. My experience is that math class is more about taking notes on the instructor’s lectures than arguing with my peers about why mathematical statements might be true or not. | 1 | 2 | 3 | 4 | 5 |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
18. In math classes, I often ask the instructor to explain why a statement is true | 1 | 2 | 3 | 4 | 5 |
|
|
|
|
|
|
20. In the past, my homework assignments usually required me to justify my thinking or explain why. | 1 | 2 | 3 | 4 | 5 |
|
|
|
|
|
|
22. In previous math classes, I have rarely had to explain my reasoning on an in-class exam. | 1 | 2 | 3 | 4 | 5 |
|
|
|
|
|
|
Part III: Circle the number that best reflects your agreement with the following:
|
|
|
|
| |
24. I think constructing proofs is an important part of doing mathematics | 1 | 2 | 3 | 4 | 5 |
|
|
|
|
|
|
26. Proofs are necessary for all areas of mathematics—not just geometry | 1 | 2 | 3 | 4 | 5 |
|
|
|
|
|
|
28. Proofs are arguments based on logic that anyone can learn to understand. | 1 | 2 | 3 | 4 | 5 |
|
|
|
|
|
|
30. It is important to me to participate in constructing mathematical arguments or proofs during instruction. | 1 | 2 | 3 | 4 | 5 |
|
|
|
|
| |
31. I believe I can learn to read and write proofs if I put enough effort into it. | 1 | 2 | 3 | 4 | 5 |
|
|
|
|
|
|
33. I feel better about my understanding of mathematics if I understand why mathematical theorems are true. | 1 | 2 | 3 | 4 | 5 |
|
|
|
|
|
|
35. In learning mathematics, it’s important for me to understand the reasons not just memorize the formulas | 1 | 2 | 3 | 4 | 5 |
|
|
|
|
|
|
37. I think students should participate in doing proofs during class time. | 1 | 2 | 3 | 4 | 5 |
|
|
|
|
| |
38. I think it is important for assessments (e.g., in-class exams) to include constructing mathematical proofs. | 1 | 2 | 3 | 4 | 5 |
39. I think I would benefit from classroom instruction that involved working in groups with my classmates to discuss how to prove mathematical statements. |
|
|
|
|
|
40. I feel that I have an important contribution to make during the construction of a proof in math class. | 1 | 2 | 3 | 4 | 5 |
Rights and permissions
Reprints and permissions
About this article
Stylianou, D.A., Blanton, M.L. & Rotou, O. Undergraduate Students’ Understanding of Proof: Relationships Between Proof Conceptions, Beliefs, and Classroom Experiences with Learning Proof. Int. J. Res. Undergrad. Math. Ed. 1 , 91–134 (2015). https://doi.org/10.1007/s40753-015-0003-0
Download citation
Published : 19 May 2015
Issue Date : April 2015
DOI : https://doi.org/10.1007/s40753-015-0003-0
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Mathematical proof
- Find a journal
- Publish with us
- Track your research
Stack Exchange Network
Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.
What is the difference between problem solving and theorem proving?Is mathematics problem solving or theorem proving?
Some books of permutation and combinations ,theorems are to proved while in some book problem is to be solved using logic.
- discrete-mathematics
- $\begingroup$ both are the same things. $\endgroup$ – Inuyasha Yagami Commented Sep 6, 2021 at 17:53
- 1 $\begingroup$ Seems better suited to Mathematics . $\endgroup$ – Yuval Filmus Commented Jun 3, 2022 at 21:55
2 Answers 2
In school, your problems are often pre-cooked exercises in which you are supposed to apply theorems or maybe prove them.
In the real world, you may encounter problems that you have no idea how to find adequate mathematical representations for, or whether such representations exist at all. Mathematical representations are abstractions: they simplify by leaving out detail, so you need to be able to simplify such that some important essence you want to reason about is captured without oversimplifying and distorting what is really going on. This can be more challenging than the subsequent work of applying or proving theorems in the representation you've chosen.
Problem solving is the art of finding the solution(s) from a problem statement. Theorem proving is the art of showing that a known solution is indisputably correct.
But if the given problem is to craft a proof, then theorem proving is an instance of problem solving. :-)
Your Answer
Sign up or log in, post as a guest.
Required, but never shown
By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy .
- Featured on Meta
- Upcoming sign-up experiments related to tags
Hot Network Questions
- In By His Bootstraps (Heinlein) why is Hitler's name Schickelgruber?
- Viewport Shader Render different from 1 computer to another
- No simple group or order 756 : Burnside's proof
- Should I accept an offer of being a teacher assistant without pay?
- Were there engineers in airship nacelles, and why were they there?
- Font shape warnings in LuaLaTeX but not XeLaTeX
- What kind of sequence is between an arithmetic and a geometric sequence?
- Can you arrange 25 whole numbers (not necessarily all different) so that the sum of any three successive terms is even but the sum of all 25 is odd?
- Rear shifter cable wont stay in anything but the highest gear
- add an apostrophe to equation number having a distant scope
- What is the translation of misgendering in French?
- How can I take apart a bookshelf?
- Where can I access records of the 1947 Superman copyright trial?
- How can I confirm for sure that a CVE has been mitigated on a RHEL system?
- Is there any other reason to stockpile minerals aside preparing for war?
- Does Matthew 7:13-14 contradict Luke 13:22-29?
- What is the term for when a hyperlink maliciously opens different URL from URL displayed when hovered over?
- Do I need to indicate 'solo' for wind/brass instruments in shared staff?
- What could explain that small planes near an airport are perceived as harassing homeowners?
- Can I get a refund for ICE due to cancelled regional bus service?
- Simple Container Class
- Does this double well potential contradict the fact that there is no degeneracy for one-dimensional bound states?
- Cleaning chain a few links at a time
- Why can't LaTeX (seem to?) Support Arbitrary Text Sizes?
Get the Reddit app
This subreddit is for discussion of mathematics. All posts and comments should be directly related to mathematics, including topics related to the practice, profession and community of mathematics.
On the relationship between proofs and problem solving. What are some of the similarities in the approach to each? What are some of the differences?

Or search by topic
Number and algebra
- The Number System and Place Value
- Calculations and Numerical Methods
- Fractions, Decimals, Percentages, Ratio and Proportion
- Properties of Numbers
- Patterns, Sequences and Structure
- Algebraic expressions, equations and formulae
- Coordinates, Functions and Graphs
Geometry and measure
- Angles, Polygons, and Geometrical Proof
- 3D Geometry, Shape and Space
- Measuring and calculating with units
- Transformations and constructions
- Pythagoras and Trigonometry
- Vectors and Matrices
Probability and statistics
- Handling, Processing and Representing Data
- Probability
Working mathematically
- Thinking mathematically
- Mathematical mindsets
- Cross-curricular contexts
- Physical and digital manipulatives
For younger learners
- Early Years Foundation Stage
Advanced mathematics
- Decision Mathematics and Combinatorics
- Advanced Probability and Statistics
Published 2018 Revised 2019
Mastering Mathematics: the Challenge of Generalising and Proof
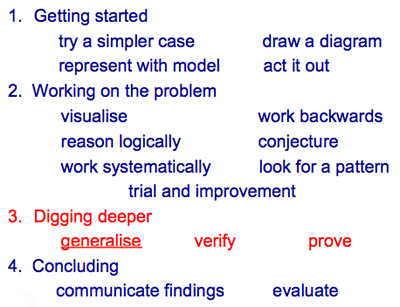
- Proof by exhaustion - this depends on there being a small number of results so that it is manageable to find all possibilities; it is about working systematically.
- Proof by counter example - an example that doesn't work disproves the conjucture.
- Proof by contradiction - we assume that what we want to prove is not true, and then show that the consequences of this are not possible.
- Proof by logical reasoning - the chain of reasoning is complete, with no room for ambiguity and no missing steps.
- Generic proof - a carefully selected example enables anyone to see, in that example, the general structure.
- Share full article
Advertisement
Supported by
Do We Need Language to Think?
A group of neuroscientists argue that our words are primarily for communicating, not for reasoning.

By Carl Zimmer
For thousands of years, philosophers have argued about the purpose of language. Plato believed it was essential for thinking. Thought “is a silent inner conversation of the soul with itself,” he wrote.
Many modern scholars have advanced similar views. Starting in the 1960s, Noam Chomsky, a linguist at M.I.T., argued that we use language for reasoning and other forms of thought. “If there is a severe deficit of language, there will be severe deficit of thought,” he wrote .
As an undergraduate, Evelina Fedorenko took Dr. Chomsky’s class and heard him describe his theory. “I really liked the idea,” she recalled. But she was puzzled by the lack of evidence. “A lot of things he was saying were just stated as if they were facts — the truth,” she said.
Dr. Fedorenko went on to become a cognitive neuroscientist at M.I.T., using brain scanning to investigate how the brain produces language. And after 15 years, her research has led her to a startling conclusion: We don’t need language to think.
“When you start evaluating it, you just don’t find support for this role of language in thinking,” she said.
When Dr. Fedorenko began this work in 2009, studies had found that the same brain regions required for language were also active when people reasoned or carried out arithmetic.
We are having trouble retrieving the article content.
Please enable JavaScript in your browser settings.
Thank you for your patience while we verify access. If you are in Reader mode please exit and log into your Times account, or subscribe for all of The Times.
Thank you for your patience while we verify access.
Already a subscriber? Log in .
Want all of The Times? Subscribe .

IMAGES
VIDEO
COMMENTS
How proofs and problem-solving are related. Proofs and problem-solving are highly interrelated. Learning to solve math problems is a great way to train your brain to think logically. You also can learn a bag of tricks that you can use later in your proofs. When tackling proofs, the more techniques you've learned, the better. But doing proofs ...
In this paper, I will consider proof from an alternative perspective, viewing proof construction as a problem-solving task. ... The relationship between problem-solving, proving and learningIn the past three decades, there has been a dramatic shift in the nature of research on mathematical problem-solving. In the 1980s, problem-solving was ...
Abstract. We expect mathematical proofs to explain why the propositions in question are true or why certain mathematical phenomena occur in certain situations. In this paper, I reexamine explanation-building processes by taking them as problem-solvers' understanding processes and by referring to research that has analyzed the relationships ...
tion-building processes by relating them to problem solvers' understanding-processes and by referring to existing research studies which analyzed relationships between their exploration, understanding, and explanation in mathematical problem solving. In the next section, the outline of the process of solving a proof problem will be presented.
In this paper I will reflect on the development of mathematical thinking in the individual learning mathematics over a life-time and relate the theory in Thinking Mathematically to a theory of the long-term development of mathematical thinking that includes the development of proof. This will be related to the work of Richard Skemp on ...
relationship to the provision of proof for problem solving. The simultaneous consideration of cognitive and affective factors makes it possible to identify factors and processes that explain the provision of proof for problem solving in a detailed and meaningful way. In addition, since Furinghetti & Morselli (2004) was a
In this paper I will reflect on the development of mathematical thinking in the individual learning mathematics over a life-time and relate the theory in Thinking Mathematically to a theory of the ...
The purposes of this paper are to describe some of the different types of reasoning and problem-solving processes used by undergraduates to construct proofs in their university mathematics courses, and to consider the relationship between the reasoning that students use when constructing a proof and what they have the opportunity to learn from ...
1.2. The relationship between problem-solving, proving and learning In the past three decades, there has been a dramatic shift in the nature of research on mathematical problem-solving. In the 1980s, problem-solving was primarily conceived of as a goal of mathematical instruction. Research
Request PDF | Problem-solving, proving, and learning: The relationship between problem-solving processes and learning opportunities in the activity of proof construction | In university ...
Problem solving and proofs have always played a major role in mathematics. They are, in fact, the heart and soul of the discipline. Even more so, using a number of different proof techniques - from
Methods of proof will include: direct, contrapositive, contradiction, and induction. Students will learn about and utilize the many functions of proof including: verification, explanation, communication, discovery, justification, and inquiry. The course will also explore the relationship between problem solving and the process of proving.
Problem-solving, proving, and learning: The relationship between problem-solving processes and learning opportunities in the activity of proof construction. / Weber, Keith. In: Journal of Mathematical Behavior, Vol. 24, No. 3-4, 2005, p. 351-360. Research output: Contribution to journal › Article › peer-review
The problem-solving process The problem-solving process can usually be thought of as having four stages, listed below ... calculator to explore the inverse relationship between addition and subtraction. You enter a 'secret number' into the calculator, then ask a child ... is the focal part of a visual proof, additional text will always be ...
dissertations. We take Schoenfeld's (1985) view of problem, namely, a mathematical task is a problem for an individual if that person does not already know a method of solution for that task. Thus, a given task may be a problem for one individual, who does not already know a solution method for that task, or it may be an exercise for an ...
This article presents the results from a study of 535 early undergraduate students at six universities that was designed to describe their views of the meaning of proof and how these views relate to their attitudes and beliefs towards proof and their classroom experiences with learning proof. Results show that early undergraduate students have difficulty with mathematical proof. In particular ...
Problem solving is the art of finding the solution(s) from a problem statement. Theorem proving is the art of showing that a known solution is indisputably correct. But if the given problem is to craft a proof, then theorem proving is an instance of problem solving.
For me personally (as a student that is), that line became blurred as I became more comfortable with proofs. Solving a problem is quite literally proving that the correct solution is, in fact, the solution. The main differences between, say, solving a quadratic equation and proving two numbers are the roots of that equation are language and method.
On Similarities and Differences between Pro ving and. Problem Solving. Milos Savic. Department of Mathematics, The University of Oklahoma, Norman OK, USA. [email protected]. Abstract. A link between ...
Abstract. Automating discovery in mathematics and science will require sophisticated methods of information extraction and abstract reasoning, including models that can convincingly process relationships between mathematical elements and natural language, to produce problem solutions of real-world value. We analyze mathematical language processing methods across five strategic sub-areas ...
Understanding the underlying structures of mathematics is fundamental to mastering the subject. This involves being fluent at generalising and proving. In this article, we look at what we mean by generalisation and proof, and how we can help learners get better at generalising and proving. The problem-solving process.
Three experiments investigate the relationship between memory and problem solving in the domain of geometry theorem proving. In Exp 1, Ss' memories for an original problem-solving episode were interfered with retroactively by solving a 2nd problem that had the same diagram, but no memory effects were observed that depended on the 2nd problem's logical similarity to the original. Results ...
A group of neuroscientists argue that our words are primarily for communicating, not for reasoning. By Carl Zimmer For thousands of years, philosophers have argued about the purpose of language ...