the black hole research paper

Black Holes

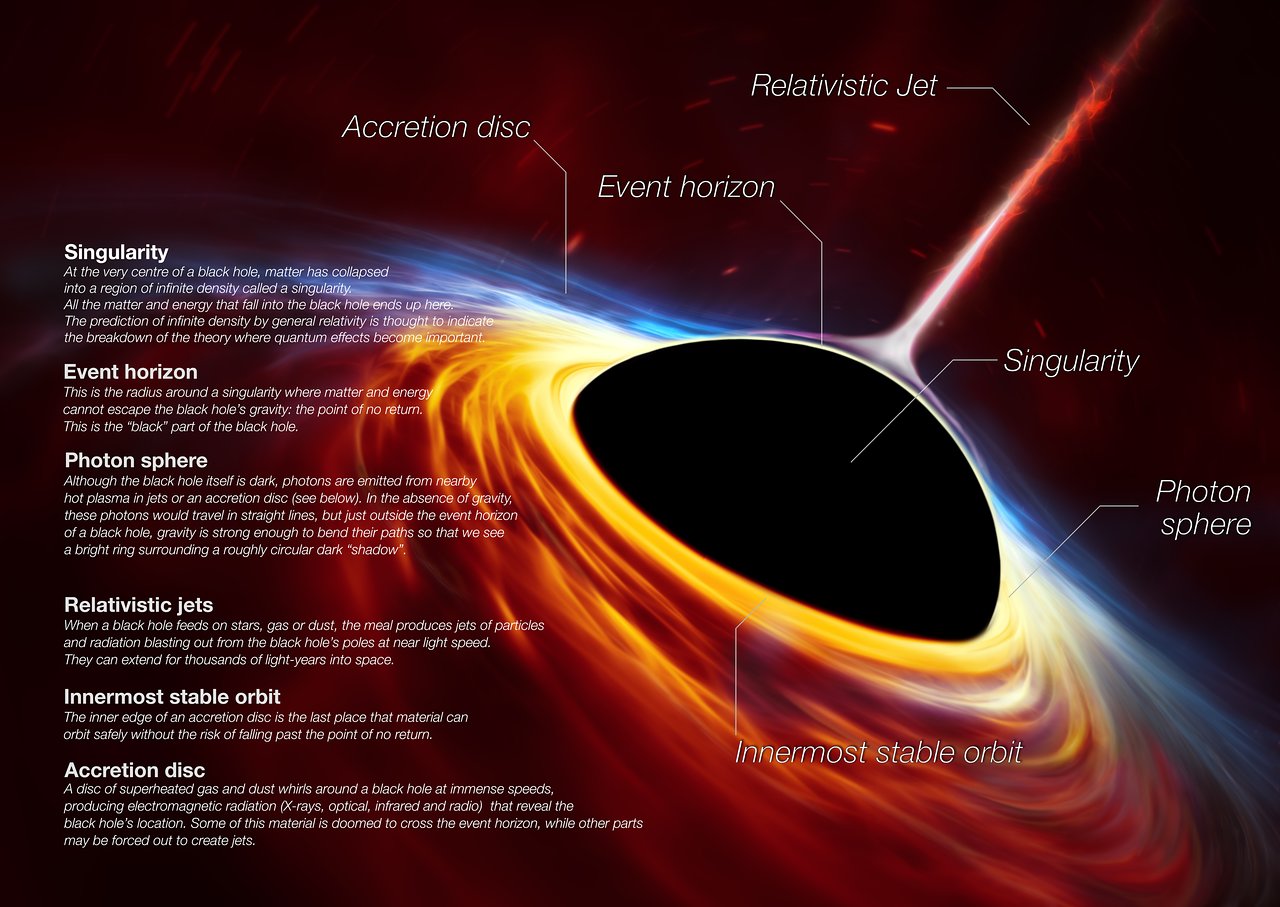
Black holes are some of the most fascinating and mind-bending objects in the cosmos. The very thing that characterizes a black hole also makes it hard to study: its intense gravity. All the mass in a black hole is concentrated in a tiny region, surrounded by a boundary called the “event horizon”. Nothing that crosses that boundary can return to the outside universe, not even light. A black hole itself is invisible.

But astronomers can still observe black holes indirectly by the way their gravity affects stars and pulls matter into orbit. As gas flows around a black hole, it heats up, paradoxically making these invisible objects into some of the brightest things in the entire universe. As a result, we can see some black holes from billions of light-years away. For one large black hole in a nearby galaxy, astronomers even managed to see a ring of light around the event horizon, using a globe-spanning array of powerful telescopes.

Center for Astrophysics | Harvard & Smithsonian scientists participate in many black hole-related projects:

Using the Event Horizon Telescope (EHT) to capture the first image of a black hole’s “shadow”: the absence of light that marks where the event horizon is located. The EHT is composed of many telescopes working together to create one Earth-sized observatory , all monitoring the supermassive black hole at the center of the galaxy M87, leading to the first image ever captured of a black hole. CfA Plays Central Role In Capturing Landmark Black Hole Image

Observing supermassive black holes in other galaxies to understand how they evolve and shape their host galaxies. CfA astronomers use telescopes across the entire spectrum of light, from radio waves to X-rays to gamma rays. A Surprising Blazar Connection Revealed

Studying the infall of matter — called “accretion” — onto black holes, using NASA’s Chandra X-ray Observatory and other telescopes. In addition, CfA researchers use cutting-edge supercomputers to create theoretical models for the disks and jets of matter that black holes create around themselves. Supermassive Black Hole Spins Super-Fast

Hunting for black hole interactions with other astronomical objects. That includes “disruption” events, where black holes tear stars or other objects apart, creating bursts of intense light. Black Hole Meal Sets Record for Length and Size

Observing clusters of stars to find intermediate mass black holes, and modeling how they shape their environments. A Middleweight Black Hole is Hiding at the Center of a Giant Star Cluster

Hunting for and characterizing stellar mass black holes, which can include information about their birth process and evolution. NASA's Chandra Adds to Black Hole Birth Announcement

The Varieties of Black Holes

Black holes come in three categories:

Stellar Mass Black Holes are born from the death of stars much more massive than the Sun. When some of these stars run out of the nuclear fuel that makes them shine, their cores collapse into black holes under their own gravity. Other stellar mass black holes form from the collision of neutron stars , such as the ones first detected by LIGO and Virgo in 2017. These are probably the most common black holes in the cosmos, but are hard to detect unless they have an ordinary star for a companion. When that happens, the black hole can strip material from the star, causing the gas to heat up and glow brightly in X-rays.

Supermassive Black Holes are the monsters of the universe, living at the centers of nearly every galaxy. They range in mass from 100,000 to billions of times the mass of the Sun, far too massive to be born from a single star. The Milky Way’s black hole is about 4 million times the Sun’s mass, putting it in the middle of the pack. In the form of quasars and other “active” galaxies , these black holes can shine brightly enough to be seen from billions of light-years away. Understanding when these black holes formed and how they grow is a major area of research. Center for Astrophysics | Harvard & Smithsonian scientists are part of the Event Horizon Telescope (EHT) collaboration, which captured the first-ever image of the black hole: the supermassive black hole at the center of the galaxy M87.

Intermediate Mass Black Holes are the most mysterious, since we’ve hardly seen any of them yet. They weigh 100 to 10,000 times the mass of the Sun, putting them between stellar and supermassive black holes. We don’t know exactly how many of these are, and like supermassive black holes, we don’t fully understand how they’re born or grow. However, studying them could tell us a lot about how the most supermassive black holes came to be.

Black holes can seem bizarre and incomprehensible, but in truth they’re remarkably understandable. Despite not being able to see black holes directly, we know quite a bit about them. They are …

Simple . All three black hole types can be described by just two observable quantities: their mass and how fast they spin. That’s much simpler than a star, for example, which in addition to mass is a product of its unique history and evolution , including its chemical makeup. Mass and spin tell us everything we need to know about a black hole: it “forgets” everything that went into making it. Those two quantities determine how big the event horizon is, and the way gravity affects any matter falling onto the black hole.

Compact . Black holes are tiny compared to their mass. The event horizon of a black hole the mass of the Sun would be no more than 6 kilometers across, and the faster it spins, the smaller that size is. Even a supermassive black hole would fit easily inside our Solar System.

Powerful . The combination of large mass and small size results in very strong gravity. This gravity is strong enough to pull a star apart if it gets too close, producing powerful bursts of light. A supermassive black hole heats gas falling onto it to temperatures of millions of degrees, making it glow brightly enough in X-rays and other types of radiation to be seen across the universe.

Very common . From theoretical calculations based on observations, astronomers think the Milky Way might have as many as a hundred million black holes, most of which are stellar mass. And with at least one supermassive black hole in most galaxies, there could be hundreds of billions of supermassive black holes in the observable universe.

Very important . Black holes have a reputation for eating everything that comes by, but they turn out to be messy eaters. A lot of stuff that falls toward a black hole gets jetted away, thanks to the complicated churning of gas near the event horizon. These jets and outflows of gas called “winds” spread atoms throughout the galaxy, and can either boost or throttle the birth of new stars, depending on other factors. That means supermassive black holes play an important role in the life of galaxies, even far beyond the black hole’s gravitational pull.

And yes, mysterious . Along with astronomers, physicists are interested in black holes because they’re a laboratory for “quantum gravity”. Black holes are described by Albert Einstein’s general relativity, which is our modern theory of gravity, but the other forces of nature are described by quantum physics. So far, nobody has developed a complete quantum gravity theory, but we already know black holes will be an important test of any proposed theory.

The first image of a black hole in human history, captured by the Event Horizon Telescope, showing light emitted by matter as it swirls under the influence of intense gravity. This black hole is 6.5 billion times the mass of the Sun and resides at the center of the galaxy M87.

• What do black holes look like?
• What happens to space time when cosmic objects collide?
• The Energetic Universe
• The Milky Way Galaxy
• Extragalactic Astronomy
• Stellar Astronomy
• Theoretical Astrophysics
• Einstein's Theory of Gravitation
• Radio and Geoastronomy

Related News

Astronomers unveil strong magnetic fields spiraling at the edge of milky way’s central black hole, black hole fashions stellar beads on a string, m87* one year later: proof of a persistent black hole shadow, unexpectedly massive black holes dominate small galaxies in the distant universe, unveiling black hole spins using polarized radio glasses, a supermassive black hole’s strong magnetic fields are revealed in a new light, nasa telescopes discover record-breaking black hole, new horizons in physics breakthrough prize awarded to cfa astrophysicist, cfa selects contractor for next generation event horizon telescope antennas, sheperd doeleman awarded the 2023 georges lemaître international prize, dasch (digital access to a sky century @ harvard), sensing the dynamic universe, champ (chandra multiwavelength project) and champlane (chandra multiwavelength plane) survey, telescopes and instruments, einstein observatory, event horizon telescope (eht), large aperture experiment to explore the dark ages (leda), the greenland telescope, very energetic radiation imaging telescope array system (veritas).

Suggestions or feedback?

MIT News | Massachusetts Institute of Technology

• Machine learning
• Social justice
• Black holes
• Classes and programs

Departments

• Aeronautics and Astronautics
• Brain and Cognitive Sciences
• Architecture
• Political Science
• Mechanical Engineering

Centers, Labs, & Programs

• Abdul Latif Jameel Poverty Action Lab (J-PAL)
• Picower Institute for Learning and Memory
• Lincoln Laboratory
• School of Architecture + Planning
• School of Engineering
• School of Humanities, Arts, and Social Sciences
• Sloan School of Management
• School of Science
• MIT Schwarzman College of Computing

Physicists observationally confirm Hawking’s black hole theorem for the first time

Press contact :, media download.

*Terms of Use:

Images for download on the MIT News office website are made available to non-commercial entities, press and the general public under a Creative Commons Attribution Non-Commercial No Derivatives license . You may not alter the images provided, other than to crop them to size. A credit line must be used when reproducing images; if one is not provided below, credit the images to "MIT."

Previous image Next image

There are certain rules that even the most extreme objects in the universe must obey. A central law for black holes predicts that the area of their event horizons — the boundary beyond which nothing can ever escape — should never shrink. This law is Hawking’s area theorem, named after physicist Stephen Hawking, who derived the theorem in 1971.

Fifty years later, physicists at MIT and elsewhere have now confirmed Hawking’s area theorem for the first time, using observations of gravitational waves. Their results appear today in Physical Review Letters .

In the study, the researchers take a closer look at GW150914, the first gravitational wave signal detected by the Laser Interferometer Gravitational-wave Observatory (LIGO), in 2015. The signal was a product of two inspiraling black holes that generated a new black hole, along with a huge amount of energy that rippled across space-time as gravitational waves.

If Hawking’s area theorem holds, then the horizon area of the new black hole should not be smaller than the total horizon area of its parent black holes. In the new study, the physicists reanalyzed the signal from GW150914 before and after the cosmic collision and found that indeed, the total event horizon area did not decrease after the merger — a result that they report with 95 percent confidence.

Their findings mark the first direct observational confirmation of Hawking’s area theorem, which has been proven mathematically but never observed in nature until now. The team plans to test future gravitational-wave signals to see if they might further confirm Hawking’s theorem or be a sign of new, law-bending physics.

“It is possible that there’s a zoo of different compact objects, and while some of them are the black holes that follow Einstein and Hawking’s laws, others may be slightly different beasts,” says lead author Maximiliano Isi, a NASA Einstein Postdoctoral Fellow in MIT’s Kavli Institute for Astrophysics and Space Research. “So, it’s not like you do this test once and it’s over. You do this once, and it’s the beginning.”

Isi’s co-authors on the paper are Will Farr of Stony Brook University and the Flatiron Institute’s Center for Computational Astrophysics, Matthew Giesler of Cornell University, Mark Scheel of Caltech, and Saul Teukolsky of Cornell University and Caltech.

An age of insights

In 1971, Stephen Hawking proposed the area theorem, which set off a series of fundamental insights about black hole mechanics. The theorem predicts that the total area of a black hole’s event horizon — and all black holes in the universe, for that matter — should never decrease. The statement was a curious parallel of the second law of thermodynamics, which states that the entropy, or degree of disorder within an object, should also never decrease.

The similarity between the two theories suggested that black holes could behave as thermal, heat-emitting objects — a confounding proposition, as black holes by their very nature were thought to never let energy escape, or radiate. Hawking eventually squared the two ideas in 1974, showing that black holes could have entropy and emit radiation over very long timescales if their quantum effects were taken into account. This phenomenon was dubbed “Hawking radiation” and remains one of the most fundamental revelations about black holes.

“It all started with Hawking’s realization that the total horizon area in black holes can never go down,” Isi says. “The area law encapsulates a golden age in the ’70s where all these insights were being produced.”

Hawking and others have since shown that the area theorem works out mathematically, but there had been no way to check it against nature until LIGO’s first detection of gravitational waves .

Hawking, on hearing of the result, quickly contacted LIGO co-founder Kip Thorne, the Feynman Professor of Theoretical Physics at Caltech. His question: Could the detection confirm the area theorem?

At the time, researchers did not have the ability to pick out the necessary information within the signal, before and after the merger, to determine whether the final horizon area did not decrease, as Hawking’s theorem would assume. It wasn’t until several years later, and the development of a technique by Isi and his colleagues, when testing the area law became feasible.

Before and after

In 2019, Isi and his colleagues developed a technique to extract the reverberations immediately following GW150914’s peak — the moment when the two parent black holes collided to form a new black hole. The team used the technique to pick out specific frequencies, or tones of the otherwise noisy aftermath, that they could use to calculate the final black hole’s mass and spin.

A black hole’s mass and spin are directly related to the area of its event horizon, and Thorne, recalling Hawking’s query, approached them with a follow-up: Could they use the same technique to compare the signal before and after the merger, and confirm the area theorem?

The researchers took on the challenge, and again split the GW150914 signal at its peak. They developed a model to analyze the signal before the peak, corresponding to the two inspiraling black holes, and to identify the mass and spin of both black holes before they merged. From these estimates, they calculated their total horizon areas — an estimate roughly equal to about 235,000 square kilometers, or roughly nine times the area of Massachusetts.

They then used their previous technique to extract the “ringdown,” or reverberations of the newly formed black hole, from which they calculated its mass and spin, and ultimately its horizon area, which they found was equivalent to 367,000 square kilometers (approximately 13 times the Bay State’s area).

“The data show with overwhelming confidence that the horizon area increased after the merger, and that the area law is satisfied with very high probability,” Isi says. “It was a relief that our result does agree with the paradigm that we expect, and does confirm our understanding of these complicated black hole mergers.”

The team plans to further test Hawking’s area theorem, and other longstanding theories of black hole mechanics, using data from LIGO and Virgo, its counterpart in Italy.

“It’s encouraging that we can think in new, creative ways about gravitational-wave data, and reach questions we thought we couldn’t before,” Isi says. “We can keep teasing out pieces of information that speak directly to the pillars of what we think we understand. One day, this data may reveal something we didn’t expect.”

This research was supported, in part, by NASA, the Simons Foundation, and the National Science Foundation.

Share this news article on:

Press mentions, popular mechanics.

Researchers from MIT and other institutions have been able to observationally confirm one of Stephen Hawking’s theorems about black holes, measuring gravitational waves before and after a black hole merger to provide evidence that a black hole’s event horizon can never shrink, reports Caroline Delbert for Popular Mechanics . “This cool analysis doesn't just show an example of Hawking's theorem that underpins one of the central laws affecting black holes,” writes Delbert, “it shows how analyzing gravitational wave patterns can bear out statistical findings.”

Previous item Next item

Related Links

• Maximiliano Isi
• MIT Kavli Institute for Astrophysics and Space Research
• LIGO Laboratory
• Department of Physics

Related Topics

• Astrophysics
• Kavli Institute
• National Science Foundation (NSF)

Related Articles

Scientists detect tones in the ringing of a newborn black hole for the first time

Quantum measurement could improve gravitational wave detection sensitivity

Could gravitational waves reveal how fast our universe is expanding?

Scientists make first direct detection of gravitational waves

More mit news.

Janabel Xia: Algorithms, dance rhythms, and the drive to succeed

Read full story →

Jonathan Byrnes, MIT Center for Transportation and Logistics senior lecturer and visionary in supply chain management, dies at 75

Researchers develop a detector for continuously monitoring toxic gases

The beauty of biology

Navigating longevity with industry leaders at MIT AgeLab PLAN Forum

Jeong Min Park earns 2024 Schmidt Science Fellowship

• More news on MIT News homepage →

Massachusetts Institute of Technology 77 Massachusetts Avenue, Cambridge, MA, USA

• Map (opens in new window)
• Events (opens in new window)
• People (opens in new window)
• Careers (opens in new window)
• Accessibility
• Social Media Hub
• MIT on Facebook
• MIT on YouTube
• MIT on Instagram

share this!

February 15, 2023

This article has been reviewed according to Science X's editorial process and policies . Editors have highlighted the following attributes while ensuring the content's credibility:

fact-checked

peer-reviewed publication

trusted source

Scientists find first evidence that black holes are the source of dark energy

by RAL Space

Observations of supermassive black holes at the centers of galaxies point to a likely source of dark energy—the 'missing' 70% of the universe.

The measurements from ancient and dormant galaxies show black holes growing more than expected, aligning with a phenomenon predicted in Einstein's theory of gravity. The result potentially means nothing new has to be added to our picture of the universe to account for dark energy: black holes combined with Einstein's gravity are the source.

The conclusion was reached by a team of 17 researchers in nine countries, led by the University of Hawai'i and including Imperial College London and STFC RAL Space physicists. The work is published in two papers in the journals The Astrophysical Journal and The Astrophysical Journal Letters .

Study co-author Dr. Dave Clements, from the Department of Physics at Imperial, said, "This is a really surprising result. We started off looking at how black holes grow over time, and may have found the answer to one of the biggest problems in cosmology."

Study co-author Dr. Chris Pearson, from STFC RAL Space, said, "If the theory holds, then this is going to revolutionize the whole of cosmology, because at last we've got a solution for the origin of dark energy that's been perplexing cosmologists and theoretical physicists for more than 20 years."

Gravity versus dark energy

In the 1990s, it was discovered that the expansion of the universe is accelerating—everything is moving away from everything else at a faster and faster rate. This is difficult to explain—the pull of gravity between all objects in the universe should be slowing the expansion down.

To account for this, it was proposed that a 'dark energy' was responsible for pushing things apart more strongly than gravity. This was linked to a concept Einstein had proposed but later discarded—a ' cosmological constant ' that opposed gravity and kept the universe from collapsing.

This concept was revived with the discovery of the accelerating expansion of the universe, with its main component being a kind of energy included in spacetime itself, called vacuum energy. This energy pushes the universe further apart, accelerating the expansion.

Black holes posed a problem though—their extremely strong gravity is hard to oppose, especially at their centers, where everything seems to break down in a phenomenon called a 'singularity.'

The new result shows that black holes gain mass in a way consistent with them containing vacuum energy, providing a source of dark energy and removing the need for singularities to form at their center.

Black hole growing pains

The conclusion was made by studying nine billion years of black hole evolution. Black holes are formed when massive stars come to the end of their life. When found at the centers of galaxies, they are called supermassive black holes . These contain millions to billions of times the mass of our Sun inside them in a comparatively small space, creating extremely strong gravity.

Black holes can increase in size by accreting matter, such as by swallowing stars that get too close, or by merging with other black holes. To discover whether these effects alone could account for the growth of supermassive black holes, the team looked at data spanning nine billion years.

The researchers looked at a particular type of galaxy called giant elliptical galaxies, which evolved early in the universe and then became dormant. Dormant galaxies have finished forming stars, leaving little material for the black hole at their center to accrete, meaning any further growth cannot be explained by these normal astrophysical processes.

Comparing observations of distant galaxies (when they were young) with local elliptical galaxies (which are old and dead) showed growth much larger than predicted by accretion or mergers: the black holes of today are 7—20 times larger than they were nine billion years ago.

Cosmological coupling

Further measurements with related populations of galaxies at different points in the universe's evolution show good agreement between the size of the universe and the mass of the black holes. These show that the measured amount of dark energy in the universe can be accounted for by black hole vacuum energy.

This is the first observational evidence that black holes actually contain vacuum energy and that they are 'coupled' to the expansion of the universe, increasing in mass as the universe expands—a phenomenon called 'cosmological coupling.' If further observations confirm it, cosmological coupling will redefine our understanding of what a black hole is.

Study first author Duncan Farrah, University of Hawai'i Astronomer and former Imperial Ph.D. student, said, "We're really saying two things at once: that there's evidence the typical black hole solutions don't work for you on a long, long timescale, and we have the first proposed astrophysical source for dark energy."

"What that means, though, is not that other people haven't proposed sources for dark energy, but this is the first observational paper where we're not adding anything new to the universe as a source for dark energy: black holes in Einstein's theory of gravity are the dark energy ."

The Astrophysical Journal Letters (2023). DOI: 10.3847/2041-8213/acb704 . iopscience.iop.org/article/10. … 847/2041-8213/acb704

Journal information: Astrophysical Journal , Astrophysical Journal Letters

Provided by RAL Space

Explore further

Feedback to editors

Composition of gut microbiota could influence decision-making

10 hours ago

Researchers realize multiphoton electron emission with non-classical light

12 hours ago

Saturday Citations: Mediterranean diet racks up more points; persistent quantum coherence; vegan dogs

Physicists propose path to faster, more flexible robots

18 hours ago

Scientists develop new geochemical 'fingerprint' to trace contaminants in fertilizer

May 17, 2024

Study reveals how a sugar-sensing protein acts as a 'machine' to switch plant growth—and oil production—on and off

Researchers develop world's smallest quantum light detector on a silicon chip

How heat waves are affecting Arctic phytoplankton

Horse remains show Pagan-Christian trade networks supplied horses from overseas for the last horse sacrifices in Europe

Ion irradiation offers promise for 2D material probing

Relevant physicsforums posts, solar activity and space weather update thread.

May 16, 2024

Light curving around vortex simulating a black hole

Our beautiful universe - photos and videos.

May 14, 2024

Strange cosmic particles in my detector

May 13, 2024

U.S. Solar Eclipses - Oct. 14, 2023 (Annular) & Apr. 08, 2024 (Total)

May 12, 2024

Exploring the Sun: Amateur Solar Imaging Techniques

More from Astronomy and Astrophysics

Related Stories

Did black holes form immediately after the Big Bang?

Dec 17, 2021

The dark side of the universe: How black holes became supermassive

Mar 11, 2022

New study suggests supermassive black holes could form from dark matter

Feb 24, 2021

Black holes and dark matter—are they one and the same?

Jan 4, 2022

Supercomputer shows 'Chameleon Theory' could change how we think about gravity

Jul 8, 2019

Dwarf galaxy Mrk 462: 'Mini' monster black hole could hold clues to giant's growth

Jan 10, 2022

Recommended for you

Astronomers detect rare neutral atomic-carbon absorbers with deep neural network

Data from MAXI J1820+070 shows Einstein was right about how matter plunges into a black hole

Into the abyss: Understanding black hole formation through natal kicks and neutrino emission

Three new RR Lyrae variable stars discovered

Webb detects most distant black hole merger to date

Astronomers discover merging twin quasars

May 15, 2024

Let us know if there is a problem with our content

Use this form if you have come across a typo, inaccuracy or would like to send an edit request for the content on this page. For general inquiries, please use our contact form . For general feedback, use the public comments section below (please adhere to guidelines ).

Please select the most appropriate category to facilitate processing of your request

Thank you for taking time to provide your feedback to the editors.

Your feedback is important to us. However, we do not guarantee individual replies due to the high volume of messages.

E-mail the story

Your email address is used only to let the recipient know who sent the email. Neither your address nor the recipient's address will be used for any other purpose. The information you enter will appear in your e-mail message and is not retained by Phys.org in any form.

Newsletter sign up

Get weekly and/or daily updates delivered to your inbox. You can unsubscribe at any time and we'll never share your details to third parties.

More information Privacy policy

Donate and enjoy an ad-free experience

We keep our content available to everyone. Consider supporting Science X's mission by getting a premium account.

E-mail newsletter

Learning Space

Teachable Moments

Stay Connected

Teachable Moments | April 19, 2019

How scientists captured the first image of a black hole.

By Ota Lutz

Find out how scientists created a virtual telescope as large as Earth itself to capture the first image of a black hole's silhouette.

Accomplishing what was previously thought to be impossible, a team of international astronomers has captured an image of a black hole’s silhouette.

Evidence of the existence of black holes – mysterious places in space where nothing, not even light, can escape – has existed for quite some time, and astronomers have long observed the effects on the surroundings of these phenomena. In the popular imagination, it was thought that capturing an image of a black hole was impossible because an image of something from which no light can escape would appear completely black. For scientists, the challenge was how, from thousands or even millions of light-years away, to capture an image of the hot, glowing gas falling into a black hole.

An ambitious team of international astronomers and computer scientists has managed to accomplish both. Working for well over a decade to achieve the feat, the team improved upon an existing radio astronomy technique for high-resolution imaging and used it to detect the silhouette of a black hole – outlined by the glowing gas that surrounds its event horizon, the precipice beyond which light cannot escape. Learning about these mysterious structures can help students understand gravity and the dynamic nature of our universe, all while sharpening their math skills.

How They Did It

Why it's important.

Though scientists had theorized they could image black holes by capturing their silhouettes against their glowing surroundings, the ability to image an object so distant still eluded them. A team formed to take on the challenge, creating a network of telescopes known as the Event Horizon Telescope, or the EHT. They set out to capture an image of a black hole by improving upon a technique that allows for the imaging of far-away objects, known as Very Long Baseline Interferometry, or VLBI.

Telescopes of all types are used to see distant objects. The larger the diameter, or aperture, of the telescope, the greater its ability to gather more light and the higher its resolution (or ability to image fine details). To see details in objects that are far away and appear small and dim from Earth, we need to gather as much light as possible with very high resolution, so we need to use a telescope with a large aperture.

That’s why the VLBI technique was essential to capturing the black hole image. VLBI works by creating an array of smaller telescopes that can be synchronized to focus on the same object at the same time and act as a giant virtual telescope. In some cases, the smaller telescopes are also an array of multiple telescopes. This technique has been used to track spacecraft and to image distant cosmic radio sources, such as quasars.

Making up one piece of the EHT array of telescopes, the Atacama Large Millimeter/submillimeter Array (ALMA) in Chile has 66 high-precision antennas. Image credit: NRAO/AUI/NSF | + Expand image

The aperture of a giant virtual telescope such as the Event Horizon Telescope is as large as the distance between the two farthest-apart telescope stations – for the EHT, those two stations are at the South Pole and in Spain, creating an aperture that’s nearly the same as the diameter of Earth. Each telescope in the array focuses on the target, in this case the black hole, and collects data from its location on Earth, providing a portion of the EHT’s full view. The more telescopes in the array that are widely spaced, the better the image resolution.

This video shows the global network of radio telescopes in the EHT array that performed observations of the black hole in the galaxy M87. Credit: C. Fromm and L. Rezzolla ( Goethe University Frankfurt )/ Black Hole Cam / EHT Collaboration | Watch on YouTube

To test VLBI for imaging a black hole and a number of computer algorithms for sorting and synchronizing data, the Event Horizon Telescope team decided on two targets, each offering unique challenges.

The closest supermassive black hole to Earth, Sagittarius A*, interested the team because it is in our galactic backyard – at the center of our Milky Way galaxy, 26,000 light-years (156 quadrillion miles) away. (An asterisk is the astronomical standard for denoting a black hole.) Though not the only black hole in our galaxy, it is the black hole that appears largest from Earth. But its location in the same galaxy as Earth meant the team would have to look through “pollution” caused by stars and dust to image it, meaning there would be more data to filter out when processing the image. Nevertheless, because of the black hole’s local interest and relatively large size, the EHT team chose Sagittarius A* as one of its two targets.

A close-up image of the core of the M87 galaxy, imaged by the Chandra X-ray Observatory. Image credit: NASA/CXC/Villanova University/J. Neilsen | + Expand image

This image from NASA's Hubble Space Telescope shows a jet of subatomic particles streaming from the center of M87*. Image credits: NASA and the Hubble Heritage Team (STScI/AURA) | + Expand image

The second target was the supermassive black hole M87*. One of the largest known supermassive black holes, M87* is located at the center of the gargantuan elliptical galaxy Messier 87, or M87, 53 million light-years (318 quintillion miles) away. Substantially more massive than Sagittarius A*, which contains 4 million solar masses, M87* contains 6.5 billion solar masses. One solar mass is equivalent to the mass of our Sun, approximately 2x10^30 kilograms. In addition to its size, M87* interested scientists because, unlike Sagittarius A*, it is an active black hole, with matter falling into it and spewing out in the form of jets of particles that are accelerated to velocities near the speed of light. But its distance made it even more of a challenge to capture than the relatively local Sagittarius A*. As described by Katie Bouman, a computer scientist with the EHT who led development of one of the algorithms used to sort telescope data during the processing of the historic image, it’s akin to capturing an image of an orange on the surface of the Moon.

By 2017, the EHT was a collaboration of eight sites around the world – and more have been added since then. Before the team could begin collecting data, they had to find a time when the weather was likely to be conducive to telescope viewing at every location. For M87*, the team tried for good weather in April 2017 and, of the 10 days chosen for observation, a whopping four days were clear at all eight sites!

Each telescope used for the EHT had to be highly synchronized with the others to within a fraction of a millimeter using an atomic clock locked onto a GPS time standard. This degree of precision makes the EHT capable of resolving objects about 4,000 times better than the Hubble Space Telescope. As each telescope acquired data from the target black hole, the digitized data and time stamp were recorded on computer disk media. Gathering data for four days around the world gave the team a substantial amount of data to process. The recorded media were then physically transported to a central location because the amount of data, around 5 petabytes, exceeds what the current internet speeds can handle. At this central location, data from all eight sites were synchronized using the time stamps and combined to create a composite set of images, revealing the never-before-seen silhouette of M87*’s event horizon. The team is also working on generating an image of Sagittarius A* from additional observations made by the EHT.

This zoom video starts with a view of the ALMA telescope array in Chile and zooms in on the heart of M87, showing successively more detailed observations and culminating in the first direct visual evidence of a supermassive black hole’s silhouette. Credit: ESO/L. Calçada, Digitized Sky Survey 2, ESA/Hubble, RadioAstron, De Gasperin et al., Kim et al., EHT Collaboration. Music: Niklas Falcke | Watch on YouTube

As more telescopes are added and the rotation of Earth is factored in, more of the image can be resolved, and we can expect future images to be higher resolution. But we might never have a complete picture, as Katie Bouman explains here (under “Imaging a Black Hole”).

To complement the EHT findings, several NASA spacecraft were part of a large effort to observe the black hole using different wavelengths of light. As part of this effort, NASA’s Chandra X-ray Observatory, Nuclear Spectroscopic Telescope Array (NuSTAR) and Neil Gehrels Swift Observatory space telescope missions – all designed to detect different varieties of X-ray light – turned their gaze to the M87 black hole around the same time as the EHT in April 2017. NASA’s Fermi Gamma-ray Space Telescope was also watching for changes in gamma-ray light from M87* during the EHT observations. If the EHT observed changes in the structure of the black hole’s environment, data from these missions and other telescopes could be used to help figure out what was going on.

Though NASA observations did not directly trace out the historic image, astronomers used data from Chandra and NuSTAR satellites to measure the X-ray brightness of M87*’s jet. Scientists used this information to compare their models of the jet and disk around the black hole with the EHT observations. Other insights may come as researchers continue to pore over these data.

Learning about mysterious structures in the universe provides insight into physics and allows us to test observation methods and theories, such as Einstein’s theory of general relativity. Massive objects deform spacetime in their vicinity, and although the theory of general relativity has directly been proven accurate for smaller-mass objects, such as Earth and the Sun, the theory has not yet been directly proven for black holes and other regions containing dense matter.

One of the main results of the EHT black hole imaging project is a more direct calculation of a black hole’s mass than ever before. Using the EHT, scientists were able to directly observe and measure the radius of M87*’s event horizon, or its Schwarzschild radius, and compute the black hole’s mass. That estimate was close to the one derived from a method that uses the motion of orbiting stars – thus validating it as a method of mass estimation.

The size and shape of a black hole, which depend on its mass and spin, can be predicted from general relativity equations. General relativity predicts that this silhouette would be roughly circular, but other theories of gravity predict slightly different shapes. The image of M87* shows a circular silhouette, thus lending credibility to Einstein’s theory of general relativity near black holes.

This artist’s impression depicts a rapidly spinning supermassive black hole surrounded by an accretion disc. Image credit: ESO | + Expand image

The data also offer some insight into the formation and behavior of black hole structures, such as the accretion disk that feeds matter into the black hole and plasma jets that emanate from its center. Scientists have hypothesized about how an accretion disk forms, but they’ve never been able to test their theories with direct observation until now. Scientists are also curious about the mechanism by which some supermassive black holes emit enormous jets of particles traveling at near light-speed.

These questions and others will be answered as more data is acquired by the EHT and synthesized in computer algorithms. Be sure to stay tuned for that and the next expected image of a black hole – our Milky Way’s own Sagittarius A*.

Update: May 12, 2022 – Scientists have released the first image of Sagittarius A* captured by the Event Horizon Telescope. › Read more from Teachable Moments

Capture your students’ enthusiasm about black holes by challenging them to solve these standards-aligned math problems .

Model black-hole interaction with this NGSS-aligned lesson:

Dropping In With Gravitational Waves

Students develop a model to represent gravitational waves and their propagation through spacetime.

Time 30 mins - 1 hr

Explore More

Video: What Is a Black Hole?

Find out how what a black hole is, how they can form and why they are so cool!

Black Holes: By the Numbers

What are black holes and how do they form?

How Do We See Dark Matter?

Students will make observations of two containers and identify differences in content, justify their claims and make comparisons to dark matter observations.

Grades 6-12

Time < 30 mins

Teachable Moment: Modeling Gravitational Waves

Find out how researchers proved part of Albert Einstein’s Theory of General Relativity, then create a model of the Nobel Prize-winning experiment in the classroom.

• JPL News: Black Hole Image Makes History
• Graphic: Anatomy of a Black Hole

Check out these related resources for students from NASA’s Space Place

• What is a Black Hole?
• Game: Black Hole Rescue!

TAGS: Black Hole , Teachable Moments , Science , K-12 Education , Teachers , Educators , Universe

Ota Lutz , K-12 Education Group Manager, NASA-JPL Education Office

Ota Lutz is the manager of the K-12 Education Group at NASA’s Jet Propulsion Laboratory. When she’s not writing new lessons or teaching, she’s probably cooking something delicious, volunteering in the community, or dreaming about where she will travel next.

• Previous Article
• Next Article

Inside the black hole

• Article contents
• Figures & tables
• Supplementary Data
• Peer Review
• Reprints and Permissions
• Cite Icon Cite
• Search Site

Robert W. Brehme; Inside the black hole. Am. J. Phys. 1 May 1977; 45 (5): 423–428. https://doi.org/10.1119/1.10829

Download citation file:

• Ris (Zotero)
• Reference Manager

The simplest model of a black hole, the massive point source generating a static spherically symmetric gravitational field, is examined using the Schwarzschild coordinate frame. A brief review is given of this coordinate frame external to the Schwarzschild surface. Greater attention is paid to an interpretation of this frame inside the Schwarzschild surface. Here the roles of space and time are reversed in the sense that the external radial coordinate becomes an internal temporal coordinate, and the external temporal coordinate becomes an internal spatial coordinate. An internal universe is constructed from this frame, and a few simple kinematic phenomena are described in terms of it. The internal and external coordinates are connected graphically by using Kruskal coordinates and physically by considering the world lines of photons and freely moving particles which transit the Schwarzschild surface.

Sign in via your Institution

Citing articles via, submit your article.

Sign up for alerts

• Online ISSN 1943-2909
• Print ISSN 0002-9505
• For Researchers
• For Librarians
• For Advertisers
• Our Publishing Partners  
• Physics Today
• Conference Proceedings
• Special Topics

pubs.aip.org

• Privacy Policy
• Terms of Use

Connect with AIP Publishing

This feature is available to subscribers only.

Sign In or Create an Account

Black holes are mysterious, yet also deceptively simple − a new space mission may help physicists answer hairy questions about these astronomical objects

Professor of Physics, University of Rhode Island

Disclosure statement

The article presents work carried out in collaboration with Stefanos Aretakis, Kevin Gonzalez-Quesada, Lior Burko, Subir Sabharwal and Som Bishoyi. This research was supported by the US National Science Foundation. All computations were performed at the Massachusetts Green High Performance Computing Center leveraging the resources of the URI Center for Computational Research. The author also acknowledges support from the UMass-URI Gravity Research Consortium (U2GRC).

University of Rhode Island provides funding as a member of The Conversation US.

View all partners

Physicists consider black holes one of the most mysterious objects that exist. Ironically, they’re also considered one of the simplest. For years, physicists like me have been looking to prove that black holes are more complex than they seem. And a newly approved European space mission called LISA will help us with this hunt.

Research from the 1970s suggests that you can comprehensively describe a black hole using only three physical attributes – their mass, charge and spin. All the other properties of these massive dying stars, like their detailed composition, density and temperature profiles, disappear as they transform into a black hole. That is how simple they are.

The idea that black holes have only three attributes is called the “no-hair” theorem, implying that they don’t have any “hairy” details that make them complicated.

Hairy black holes?

For decades, researchers in the astrophysics community have exploited loopholes or work-arounds within the no-hair theorem’s assumptions to come up with potential hairy black hole scenarios. A hairy black hole has a physical property that scientists can measure – in principle – that’s beyond its mass, charge or spin. This property has to be a permanent part of its structure.

About a decade ago, Stefanos Aretakis , a physicist currently at the University of Toronto, showed mathematically that a black hole containing the maximum charge it could hold – called an extremal charged black hole – would develop “hair” at its horizon. A black hole’s horizon is the boundary where anything that crosses it, even light, can’t escape.

Aretakis’ analysis was more of a thought experiment using a highly simplified physical scenario, so it’s not something scientists expect to observe astrophysically. But supercharged black holes might not be the only kind that could have hair.

Since astrophysical objects such as stars and planets are known to spin, scientists expect that black holes would spin as well , based on how they form. Astronomical evidence has shown that black holes do have spin, though researchers don’t know what the typical spin value is for an astrophysical black hole.

Using computer simulations, my team has recently discovered similar types of hair in black holes that are spinning at the maximum rate. This hair has to do with the rate of change, or the gradient, of space-time’s curvature at the horizon. We also discovered that a black hole wouldn’t actually have to be maximally spinning to have hair, which is significant because these maximally spinning black holes probably don’t form in nature.

Detecting and measuring hair

My team wanted to develop a way to potentially measure this hair – a new fixed property that might characterize a black hole beyond its mass, spin and charge. We started looking into how such a new property might leave a signature on a gravitational wave emitted from a fast-spinning black hole.

A gravitational wave is a tiny disturbance in space-time typically caused by violent astrophysical events in the universe. The collisions of compact astrophysical objects such as black holes and neutron stars emit strong gravitational waves. An international network of gravitational observatories, including the Laser Interferometer Gravitational-wave Observatory in the United States, routinely detects these waves.

Our recent studies suggest that one can measure these hairy attributes from gravitational wave data for fast-spinning black holes . Looking at the gravitational wave data offers an opportunity for a signature of sorts that could indicate whether the black hole has this type of hair.

Our ongoing studies and recent progress made by Som Bishoyi, a student on the team, are based on a blend of theoretical and computational models of fast-spinning black holes. Our findings have not been tested in the field yet or observed in real black holes out in space. But we hope that will soon change.

LISA gets a go-ahead

In January 2024, the European Space Agency formally adopted the space-based Laser Interferometer Space Antenna , or LISA, mission. LISA will look for gravitational waves, and the data from the mission could help my team with our hairy black hole questions.

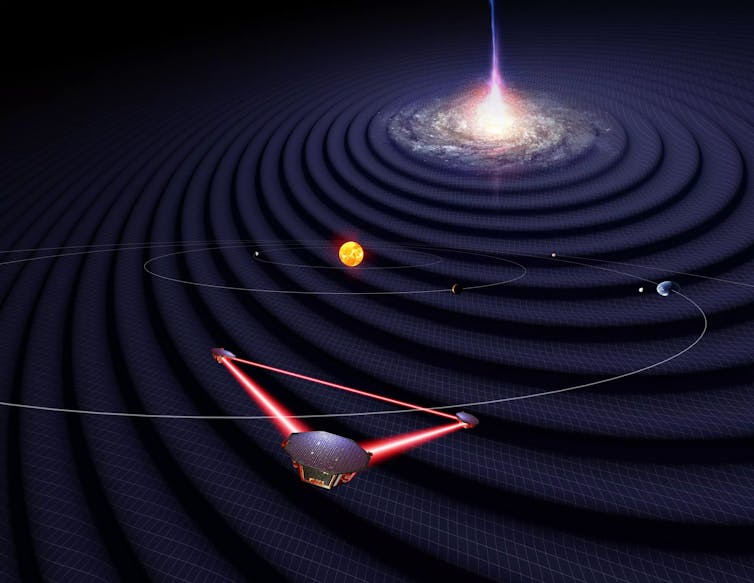
Formal adoption means that the project has the go-ahead to move to the construction phase, with a planned 2035 launch. LISA consists of three spacecrafts configured in a perfect equilateral triangle that will trail behind the Earth around the Sun. The spacecrafts will each be 1.6 million miles (2.5 million kilometers) apart , and they will exchange laser beams to measure the distance between each other down to about a billionth of an inch.

LISA will detect gravitational waves from supermassive black holes that are millions or even billions of times more massive than our Sun. It will build a map of the space-time around rotating black holes, which will help physicists understand how gravity works in the close vicinity of black holes to an unprecedented level of accuracy. Physicists hope that LISA will also be able to measure any hairy attributes that black holes might have.

With LIGO making new observations every day and LISA to offer a glimpse into the space-time around black holes, now is one of the most exciting times to be a black hole physicist.

• Astrophysics
• Black holes
• Gravitational waves
• Gravitational wave detector

Compliance Lead

Lecturer / Senior Lecturer - Marketing

Assistant Editor - 1 year cadetship

Executive Dean, Faculty of Health

Lecturer/Senior Lecturer, Earth System Science (School of Science)

Accessibility Links

• Skip to content
• Skip to search IOPscience
• Skip to Journals list
• Accessibility help
• Accessibility Help

Click here to close this panel.

Purpose-led Publishing is a coalition of three not-for-profit publishers in the field of physical sciences: AIP Publishing, the American Physical Society and IOP Publishing.

Together, as publishers that will always put purpose above profit, we have defined a set of industry standards that underpin high-quality, ethical scholarly communications.

We are proudly declaring that science is our only shareholder.

Gravitational lensing by spinning black holes in astrophysics, and in the movie Interstellar

Oliver James 3,1 , Eugénie von Tunzelmann 1 , Paul Franklin 1 and Kip S Thorne 2

Published 13 February 2015 • © 2015 IOP Publishing Ltd Classical and Quantum Gravity , Volume 32 , Number 6 Citation Oliver James et al 2015 Class. Quantum Grav. 32 065001 DOI 10.1088/0264-9381/32/6/065001

Article metrics

353971 Total downloads 60970 Video abstract views

Share this article

Author e-mails.

[email protected]

[email protected]

[email protected]

[email protected]

Author affiliations

1 Double Negative Ltd., 160 Great Portland Street, London W1W 5QA, UK

2 Walter Burke Institute for Theoretical Physics, California Institute of Technology, Pasadena, California 91125, USA

Author notes

3 Author to whom any correspondence should be addressed.

• Received 27 November 2014
• Revised 12 January 2015
• Accepted 13 January 2015
• Published 13 February 2015

Peer review information

Method : Single-anonymous Revisions: 1 Screened for originality? No

Buy this article in print

Interstellar is the first Hollywood movie to attempt depicting a black hole as it would actually be seen by somebody nearby. For this, our team at Double Negative Visual Effects , in collaboration with physicist Kip Thorne, developed a code called Double Negative Gravitational Renderer (DNGR) to solve the equations for ray-bundle (light-beam) propagation through the curved spacetime of a spinning (Kerr) black hole, and to render IMAX-quality, rapidly changing images. Our ray-bundle techniques were crucial for achieving IMAX-quality smoothness without flickering; and they differ from physicists' image-generation techniques (which generally rely on individual light rays rather than ray bundles), and also differ from techniques previously used in the film industry's CGI community. This paper has four purposes: (i) to describe DNGR for physicists and CGI practitioners, who may find interesting and useful some of our unconventional techniques. (ii) To present the equations we use, when the camera is in arbitrary motion at an arbitrary location near a Kerr black hole, for mapping light sources to camera images via elliptical ray bundles. (iii) To describe new insights, from DNGR, into gravitational lensing when the camera is near the spinning black hole, rather than far away as in almost all prior studies; we focus on the shapes, sizes and influence of caustics and critical curves, the creation and annihilation of stellar images, the pattern of multiple images, and the influence of almost-trapped light rays, and we find similar results to the more familiar case of a camera far from the hole. (iv) To describe how the images of the black hole Gargantua and its accretion disk, in the movie Interstellar , were generated with DNGR—including, especially, the influences of (a) colour changes due to doppler and gravitational frequency shifts, (b) intensity changes due to the frequency shifts, (c) simulated camera lens flare, and (d) decisions that the film makers made about these influences and about the Gargantua's spin, with the goal of producing images understandable for a mass audience. There are no new astrophysical insights in this accretion-disk section of the paper, but disk novices may find it pedagogically interesting, and movie buffs may find its discussions of Interstellar interesting.

Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence . Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.

1. Introduction and overview

1.1. previous research and visualizations.

At a summer school in Les Houches, France, in summer 1972, Bardeen [ 1 ], building on earlier work of Carter [ 2 ], initiated research on gravitational lensing by spinning black holes. Bardeen gave a thorough analytical analysis of null geodesics (light-ray propagation) around a spinning black hole; and, as part of his analysis, he computed how a black hole's spin affects the shape of the shadow that the hole casts on light from a distant star field. The shadow bulges out on the side of the hole moving away from the observer, and squeezes inward and flattens on the side moving toward the observer. The result, for a maximally spinning hole viewed from afar, is a D-shaped shadow; cf figure 4 . (When viewed up close, the shadow's flat edge has a shallow notch cut out of it, as hinted by figure 8 .)

Despite this early work, gravitational lensing by black holes remained a backwater of physics research until decades later, when the prospect for actual observations brought it to the fore.

There were, we think, two especially memorable accomplishments in the backwater era. The first was a 1978 simulation of what a camera sees as it orbits a non-spinning black hole, with a star field in the background. This simulation was carried out by Palmer et al [ 3 ] on an Evans and Sutherland vector graphics display at Simon Fraser University. Palmer et al did not publish their simulation, but they showed a film clip from it in a number of lectures in that era. The nicest modern-era film clip of this same sort that we know of is by Riazuelo (contained in his DVD [ 4 ] and available on the web at [ 5 ]); see figure 3 and associated discussion. And see [ 6 ] for an online application by Müller and Weiskopf for generating similar film clips. Also of much interest in our modern era are film clips by Hamilton [ 7 ] of what a camera sees when falling into a nonspinning black hole; these have been shown at many planetariums, and elsewhere.

The other most memorable backwater-era accomplishment was a black and white simulation by Luminet [ 8 ] of what a thin accretion disk, gravitationally lensed by a nonspinning black hole, would look like as seen from far away but close enough to resolve the image. In figure 15 (c), we show a modern-era colour version of this, with the camera close to a fast-spinning black hole.

Gravitational lensing by black holes began to be observationally important in the 1990s. Rauch and Blandford [ 9 ] recognized that, when a hot spot, in a black hole's accretion disk or jet, passes through caustics of the Earth's past light cone (caustics produced by the hole's spacetime curvature), the brightness of the hot spot's x-rays will undergo sharp oscillations with informative shapes. This has motivated a number of quantitative studies of the Kerr metric's caustics; see, especially [ 9 – 11 ] and references therein.

In the 1990s astrophysicists began to envision an era in which very long baseline interferometry would make possible the imaging of black holes—specifically, their shadows and their accretion disks. This motivated visualizations, with ever increasing sophistication, of accretion disks around black holes: modern variants of Luminet's [ 8 ] pioneering work. See, especially, Fukue and Yokoyama [ 13 ], who added colours to the disk; Viergutz [ 14 ], who made his black hole spin, treated thick disks, and produced particularly nice and interesting coloured images and included the disk's secondary image which wraps under the black hole; Marck [ 15 ], who laid the foundations for a lovely movie now available on the web [ 16 ] with the camera moving around close to the disk, and who also included higher-order images, as did Fanton et al [ 17 ] and Beckwith and Done [ 18 ]. See also papers cited in these articles.

In the 2000s astrophysicists have focused on perfecting the mm-interferometer imaging of black-hole shadows and disks, particularly the black hole at the centre of our own Milky Way Galaxy (Sgr A*). See, e.g., the 2000 feasibility study by Falcke et al [ 19 ]. See also references on the development and exploitation of general relativistic magnetohydrodynamical (GRMHD) simulation codes for modelling accretion disks like that in Sgr A* [ 20 – 22 ]; and references on detailed GRMHD models of Sgr A* and the models' comparison with observations [ 23 – 26 ]. This is culminating in a mm interferometric system called the Event Horizon Telescope [ 27 ], which is beginning to yield interesting observational results though not yet full images of the shadow and disk in Sgr A*.

All the astrophysical visualizations of gravitational lensing and accretion disks described above, and all others that we are aware of, are based on tracing huge numbers of light rays through curved spacetime. A primary goal of today's state-of-the-art, astrophysical ray-tracing codes (e.g., the Chan et al massively parallel, GPU-based code GRay [ 28 ]) is very fast throughput, measured, e.g., in integration steps per second; the spatial smoothness of images has been only a secondary concern. For our Interstellar work, by contrast, a primary goal is smoothness of the images, so flickering is minimized when objects move rapidly across an IMAX screen; fast throughput has been only a secondary concern.

With these different primary goals, in our own code, called Double Negative Gravitational Renderer (DNGR), we have been driven to employ a different set of visualization techniques from those of the astrophysics community—techniques based on propagation of ray bundles (light beams) instead of discrete light rays, and on carefully designed spatial filtering to smooth the overlaps of neighbouring beams; see section 2 and appendix A . Although, at Double Negative, we have many GPU-based workstations, the bulk of our computational work is done on a large compute cluster (the Double Negative render-farm) that does not employ GPUs.

In appendix A.7 we shall give additional comparisons of our DNGR code with astrophysical codes and with other film-industry CGI codes.

1.2. This paper

Our work on gravitational lensing by black holes began in May 2013, when Christopher Nolan asked us to collaborate on building realistic images of a spinning black hole and its disk, with IMAX resolution, for his science-fiction movie Interstellar . We saw this not only as an opportunity to bring realistic black holes into the Hollywood arena, but also an opportunity to create a simulation code capable of exploring a black hole's lensing with a level of image smoothness and dynamics not previously available.

To achieve IMAX quality (with 23 million pixels per image and adequately smooth transitions between pixels), our code needed to integrate not only rays (photon trajectories) from the light source to the simulated camera, but also bundles of rays (light beams) with filtering to smooth the beams' overlap; see section 2 , appendices A.2 , and A.3 . And because the camera would sometimes be moving with speeds that are a substantial fraction of the speed of light, our code needed to incorporate relativistic aberration as well as Doppler shifts and gravitational redshifts.

Thorne, having had a bit of experience with this kind of stuff, put together a step-by-step prescription for how to map a light ray and ray bundle from the light source (the celestial sphere or an accretion disk) to the camera's local sky; see appendices A.1 and A.2 . He implemented his prescription in Mathematica to be sure it produced images in accord with others' prior simulations and his own intuition. He then turned his prescription over to our Double Negative team, who created the fast, high-resolution code DNGR that we describe in section 2 and appendix A , and created the images to be lensed: fields of stars and in some cases also dust clouds, nebulae, and the accretion disk around Interstellar 's black hole, Gargantua.

Finally, in section 5 we summarize and we point to our use of DNGR to produce images of gravitational lensing by wormholes.

Throughout we use geometrized units in which G (Newton's gravitation constant) and c (the speed of light) are set to unity, and we use the MTW sign conventions [ 33 ].

2. DNGR: our Double Negative Gravitational Renderer code

Our computer code for making images of what a camera would see in the vicinity of a black hole or wormhole is called the Double Negative Gravitational Renderer, or DNGR—which obviously can also be interpreted as the Double Negative General Relativistic code.

2.1. Ray tracing

The ray tracing part of DNGR produces a map from the celestial sphere (or the surface of an accretion disk) to the camera's local sky. More specifically (see appendix A.1 for details and figure 1 for the ray-tracing geometry):

• (vi)   If the ray originates on the surface of an accretion disk, we integrate the null geodesic equation backward from the camera until it hits the disk's surface, and thereby deduce the map from a point on the disk's surface to one on the camera's sky. For more details on this case, see appendix A.6 .
• (vii)   We also compute, using the relevant Doppler shift and gravitational redshift, the net frequency shift from the ray's source to the camera, and the corresponding net change in light intensity.

Download figure:

2.2. Ray-bundle (light-beam) propagation

DNGR achieves its IMAX-quality images by integrating a bundle of light rays (a light beam) backward along the null geodesic from the camera to the celestial sphere using a slightly modified variant of a procedure formulated in the 1970s by Pineault and Roeder [ 35 , 36 ]. This procedure is based on the equation of geodesic deviation and is equivalent to the optical scalar equations [ 37 ] that have been widely used by astrophysicists in analytical (but not numerical) studies of gravitational lensing; see references in section 2.3 of [ 38 ]. Our procedure, in brief outline, is this (see figure 1 ); for full details, see appendix A.2 .

• (i)   In DNGR, we begin with an initially circular (or sometimes initially elliptical) bundle of rays, with very small opening angle, centred on a pixel on the camera's sky.
• (iii)   We then add up the spectrum and intensity of all the light emitted from within that ellipse; and thence, using the frequency and intensity shifts that were computed by ray tracing, we deduce the spectrum and intensity of the light arriving in the chosen camera pixel.

2.3. Filtering, implementation, and code characteristics

Novel types of filtering are key to generating our IMAX-quality images for movies. In DNGR we use spatial filtering to smooth the interfaces between beams (ray bundles), and temporal filtering to make dynamical images look like they were filmed with a movie camera. For details, see appendix A.3 .

In appendix A.4 we describe some details of our DNGR implementation of the ray-tracing, ray-bundle, and filtering equations; in appendix A.5 we describe some characteristics of our code and of Double Negative's Linux-based render-farm on which we do our computations; in appendix A.6 we describe our DNGR modelling of accretion disks; and in appendix A.7 we briefly compare DNGR with other film-industry CGI codes and state-of-the-art astrophysical simulation codes.

3. Lensing of a star field as seen by a moving camera near a black hole

3.1. nonspinning black hole.

In this subsection we review well known features of gravitational lensing by a nonspinning (Schwarzschild) black hole, in preparation for discussing the same things for a fast-spinning hole.

Images outside the Einstein ring (the violet circle) move rightward and deflect away from the ring. These are called primary images . Images inside the Einstein ring ( secondary images ) appear, in the film clip, to emerge from the edge of the black hole's shadow, loop leftward around the hole, and descend back into the shadow. However, closer inspection with higher resolution reveals that their tracks actually close up along the shadow's edge as shown in the figure; the close-up is not seen in the film clip because the images are so very dim along the inner leg of their tracks. At all times, each star's two images are on opposite sides of the shadow's centre.

This behaviour is generic. Every star (if idealized as a point source of light), except a set of measure zero, has two images that behave in the same manner as the red and yellow ones. Outside the Einstein ring, the entire primary star field flows rightward, deflecting around the ring; inside the ring, the entire secondary star field loops leftward, confined by the ring then back rightward along the shadow's edge. (There actually are more, unseen, images of the star field, even closer to the shadow's edge, that we shall discuss in section 3.2 .)

As is well known, this behaviour is easily understood by tracing light rays from the camera to the celestial sphere; see figure 3 .

The Einstein ring is the image, on the camera's sky, of a point source that is on the celestial sphere, diametrically opposite the camera; i.e., at the location indicated by the red dot and labeled 'Caustic' in figure 3 . Light rays from that caustic point generate the purple ray surface that converges on the camera, and the Einstein ring is the intersection of that ray surface with the camera's local sky.

(The caustic point (red dot) is actually the intersection of the celestial sphere with a caustic line (a one-dimensional sharp edge) on the camera's past light cone. This caustic line extends radially from the black hole's horizon to the caustic point.)

The figure shows a single star (black dot) on the celestial sphere and two light rays that travel from that star to the camera, gravitationally deflecting around opposite sides of the black hole. One of these rays, the primary one, arrives at the camera outside the Einstein ring; the other, secondary ray, arrives inside the Einstein ring.

Because the caustic point and the star on the celestial sphere both have dimension zero, as the camera moves, causing the caustic point to move relative to the star, there is zero probability for it to pass through the star. Therefore, the star's two images will never cross the Einstein ring; one will remain forever outside it and the other inside—and similarly for all other stars in the star field.

However, if a star with finite size passes close to the ring, the gravitational lensing will momentarily stretch its two images into lenticular shapes that hug the Einstein ring and will produce a great, temporary increase in each image's energy flux at the camera due to the temporary increase in the total solid angle subtended by each lenticular image. This increase in flux still occurs when the star's actual size is too small for its images to be resolved, and also in the limit of a point star. For examples, see Riazuelo's film clip [ 5 ].

(Large amplifications of extended images are actually seen in nature, for example in the gravitational lensing of distant galaxies by more nearby galaxies or galaxy clusters; see, e.g. [ 39 ].)

3.2. Fast-spinning black hole: introduction

In the figure we show in violet two critical curves—analogs of the Einstein ring for a nonspinning black hole. These are images, on the camera sky, of two caustic curves that reside on the celestial sphere; see discussion below.

We shall discuss in turn the region outside the secondary (inner) critical curve, and then the region inside.

3.3. Fast-spinning hole: outer region—outside the secondary critical curve

As the camera moves through one full orbit around the hole, the stellar images in the outer region make one full circuit along the red and yellow curves and other curves like them, largely avoiding the two critical curves of figure 4 —particularly the outer (primary) one.

(For a nonspinning black hole (figure 2 ) there are also two critical curves, with the stellar-image motions confined by them: the Einstein ring, and a circular inner critical curve very close to the black hole's shadow, that prevents the inner star tracks from plunging into the shadow and deflects them around the shadow so they close up.)

3.3.1. Primary and secondary critical curves and their caustics

After seeing these stellar-image motions in our simulations, we explored the nature of the critical curves and caustics for a camera near a fast-spinning black hole, and their influence. Our exploration, conceptually, is a rather straightforward generalization of ideas laid out by Rauch and Blandford [ 9 ] and by Bozza [ 10 ]. They studied a camera or observer on the celestial sphere and light sources orbiting a black hole; our case is the inverse: a camera orbiting the hole and light sources on the celestial sphere.

Just as the Einstein ring, for a nonspinning black hole, is the image of a caustic point on the celestial sphere—the intersection of the celestial sphere with a caustic line on the camera's past light cone—so the critical curves for our spinning black hole are also images of the intersection of the celestial sphere with light-cone caustics. But the spinning hole's light-cone caustics generically are two-dimensional (2D) surfaces (folds) in the three-dimensional light cone, so their intersections with the celestial sphere are one-dimensional: they are closed caustic curves in the celestial sphere, rather than caustic points. The hole's rotation breaks spherical symmetry and converts non-generic caustic points into generic caustic curves. (For this reason, theorems about caustics in the Schwarzschild spacetime, which are rather easy to prove, are of minor importance compared to results about generic caustics in the Kerr spacetime.)

Figure 3.  Light rays around a Schwarzschild black hole: geometric construction for explaining figure 2 .

3.3.2. Image creations and annihilations on critical curves

Because the spinning hole's caustics have finite cross sections on the celestial sphere, by contrast with the point caustics of a nonspinning black hole, stars, generically, can cross through them; see, e.g., the dashed stellar path in figure 5 . As is well known from the elementary theory of fold caustics (see, e.g., section 7.5 of [ 41 ]), at each crossing two stellar images, on opposite sides of the caustic's critical curve, merge and annihilate; or two are created. And at the moment of creation or annihilation, the images are very bright.

The primary track (order 0) does not intersect the primary critical curve, so a single primary image travels around it as the camera orbits the black hole. The secondary track (order 1) is the one depicted red in figure 6 and discussed above. It crosses the secondary critical curve twice, so there is a single pair creation event and a single annihilation event; at some times there is a single secondary image on the track, and at others there are three. It is not clear to us whether the red secondary track crosses the tertiary critical curve (not shown); but if it does, there will be no pair creations or annihilations at the crossing points, because the secondary track and the tertiary critical curve are generated by rays with different numbers of poloidal turning points, and so the critical curve is incapable of influencing images on the track. The extension to higher-order tracks and critical curves, all closer to the hole's shadow, should be clear. This pattern is qualitatively the same as when the light source is near the black hole and the camera far away, but in the hole's equatorial plane [ 11 ].

The film clips at stacks.iop.org/cqg/32/065001/mmedia exhibit these tracks and images all together, and show a plethora of image creations and annihilations. Exploring these clips can be fun and informative.

3.4. Fast-spinning hole: inner region—inside the secondary critical curve

The version of DNGR that we used for Interstellar showed a surprisingly complex, fingerprint-like structure of gravitationally lensed stars inside the secondary critical curve, along the left side of the shadow.

We searched for errors that might be responsible for it, and finding none, we thought it real. But Riazuelo [ 42 ] saw nothing like it in his computed images. Making detailed comparisons with Riazuelo, we found a bug in DNGR. When we corrected the bug, the complex pattern went away, and we got excellent agreement with Riazuelo (when using the same coordinate system), and with images produced by Bohn et al using their Cornell/Caltech SXS imaging code [ 43 ]. Since the SXS code is so very different from ours (it is designed to visualize colliding black holes), that agreement gives us high confidence in the results reported below.

Fortunately, the bug we found had no noticeable impact on the images in Interstellar .

With our debugged code, the inner region, inside the secondary critical curve, appears to be a continuation of the pattern seen in the exterior region. There is a third critical curve within the second, and there are signs of higher-order critical curves, all nested inside each other. These are most visible near the flattened edge of the black hole's shadow on the side where the horizon's rotation is toward the camera (the left side in this paper's figures). The dragging of inertial frames moves the critical curves outward from the shadow's flattened edge, enabling us to see things that otherwise could only be seen with a strong zoom-in.

3.4.1. Critical curves and caustics for {{r}_{c}}=2.60M

Figure 9.  (a) The secondary caustic (red) on the celestial sphere and secondary critical curve (green) on the camera's sky, for the black hole and camera of figure 8 . Points on each curve that are ray-mapped images of each other are marked by letters a, b, c, d. (b) The tertiary caustic and tertiary critical curve.

3.4.2. Multiple images for {{r}_{c}}=2.60M

Returning to the gravitationally lensed star-field image in figure 8 (b): notice the series of images of the galactic plane (fuzzy white curves). Above and below the black hole's shadow there is just one galactic-plane image between the primary and secondary critical curves, and just one between the secondary and tertiary critical curves. This is what we expect from the example of a nonspinning black hole. However, near the fast-spinning hole's left shadow edge, the pattern is very different: three galactic-plane images between the primary and secondary critical curves, and eight between the secondary and tertiary critical curves.

These multiple galactic-plane images are caused by the large sizes of the caustics—particularly their wrapping around the celestial sphere—and the resulting ease with which stars cross them, producing multiple stellar images. An extension of an argument by Bozza [ 10 ] (paragraph preceding his equation (17)) makes this more precise. (This argument will be highly plausible but not fully rigorous because we have not developed a sufficiently complete understanding to make it rigorous.)

When above the caustics, the star produces one image of each order: A primary image (no poloidal turning points) that presumably will remain outside the primary critical curve when the star returns to its equatorial location; a secondary image (one poloidal turning point) that presumably will be between the primary and secondary critical curves when the star returns; a tertiary image between the secondary and tertiary critical curves; etc.

When the star moves downward through the upper left branch of the astroidal primary caustic, it creates two primary images, one on each side of the primary critical curve. When it moves downward through the upper left branch of the secondary caustic (figure 9 (a)), it creates two secondary images, one on each side of the secondary caustic. And when it moves downward through the six sky-wrapped upper left branches of the tertiary caustic (figure 9 (b)), it creates 12 tertiary images, six on each side of the tertiary caustic. And because the upper left branches of all three caustics map onto the left sides of their corresponding critical curves, all the created images will wind up on the left sides of the critical curves and thence the left side of the black hole's shadow. And by symmetry, with the camera and the star both in the equatorial plane, all these images will wind up in the equatorial plane.

So now we can count. In the equatorial plane to the left of the primary critical curve, there are two images: one original primary image, and one caustic-created primary image. These are to the left of the region depicted in figure 8 (a). Between the primary and secondary critical curves there are three images: one original secondary image, one caustic-created primary, and one caustic-created secondary image. These are representative stellar images in the three galactic-plane images between the primary and secondary critical curves of figure 8 . And between the secondary and tertiary critical curves there are eight stellar images: one original tertiary, one caustic-created secondary, and six caustic-created tertiary images. These are representative stellar images in the eight galactic-plane images between the secondary and tertiary critical curves of figure 8 .

3.4.3. Checkerboard to elucidate the multiple-image pattern

Figure 10 is designed to help readers explore this multiple-image phenomenon in greater detail. There we have placed, on the celestial sphere, a checkerboard of paint swatches (figure 10 (a)), with dashed lines running along the constant-latitude spaces between paint swatches, i.e., along the celestial-sphere tracks of stars. In figure 10 (b) we show the gravitationally lensed checkerboard on the camera's entire sky; and in figure 10 (c) we show a blowup of the camera-sky region near the left edge of the black hole's shadow. We have labeled the critical curves 1CC, 2CC and 3CC for primary, secondary, and tertiary.

The multiple images of lines of constant celestial-sphere longitude show up clearly in the blow-up, between pairs of critical curves; and the figure shows those lines being stretched vertically, enormously, in the vicinity of each critical curve. The dashed lines (star-image tracks) on the camera's sky show the same kind of pattern as we saw in figure 7 .

3.4.4. Multiple images explained by light-ray trapping

The multiple images near the left edge of the shadow can also be understood in terms of the light rays that bring the stellar images to the camera. Those light rays travel from the celestial sphere inward to near the black hole, where they get temporarily trapped, for a few round-trips, on near circular orbits (orbits with nearly constant Boyer–Lindquist radius r ), and then escape to the camera. Each such nearly trapped ray is very close to a truly (but unstably) trapped, constant- r ray such as that shown in figure 11 . These trapped rays (discussed in [ 45 ] and in chapters 6 and 8 of [ 40 ]) wind up and down spherical strips with very shallow pitch angles.

As the camera makes each additional prograde trip around the black hole, the image carried by each temporarily trapped mapping ray gets wound around the constant- r sphere one more time (i.e., gets stored there for one more circuit), and it comes out to the camera's sky slightly closer to the shadow's edge and slightly higher or lower in latitude. Correspondingly, as the camera moves, the star's image gradually sinks closer to the hole's shadow and gradually changes its latitude—actually moving away from the equator when approaching a critical curve and toward the equator when receding from a critical curve. This behaviour is seen clearly, near the shadow's left edge, in the film clips at stacks.iop.org/cqg/32/065001/mmedia .

3.5. Aberration: influence of the camera's speed

Despite these huge differences in lensing patterns, the multiplicity of images between critical curves is unchanged: still three images of some near-equator swatches between the primary and secondary critical curves, and eight between the secondary and tertiary critical curves. This is because the caustics in the camera's past light cone depend only on the camera's location and not on its velocity, so a point source's caustic crossings are independent of camera velocity, and the image pair creations and annihilations along critical curves are independent of camera velocity.

4. Lensing of an accretion disk

4.1. effects of lensing, colour shift, and brightness shift: a pedagogical discussion.

We have used our code, DNGR, to construct images of what a thin accretion disk in the equatorial plane of a fast-spinning black hole would look like, seen up close. For our own edification, we explored successively the influence of the bending of light rays (gravitational lensing), the influence of Doppler frequency shifts and gravitational frequency shifts on the disk's colours, the influence of the frequency shifts on the brightness of the disk's light, and the influence of lens flare due to light scattering and diffraction in the lenses of a simulated 65 mm IMAX camera. Although all these issues except lens flare have been explored previously, e.g. in [ 8 , 13 , 14 , 17 , 18 ] and references therein, our images may be of pedagogical interest, so we show them here. We also show them as a foundation for discussing the choices that were made for Interstellar ' s accretion disk.

4.1.1. Gravitational lensing

In the figure we see three images of the disk. The upper image swings around the front of the black hole's shadow and then, instead of passing behind the shadow, it swings up over the shadow and back down to close on itself. This wrapping over the shadow has a simple physical origin: light rays from the top face of the disk, which is actually behind the hole, pass up over the top of the hole and down to the camera due to gravitational light deflection; see figure 9.8 of [ 40 ]. This entire image comes from light rays emitted by the disk's top face. By looking at the colours, lengths, and widths of the disk's swatches and comparing with those in the inset, one can deduce, in each region of the disk, the details of the gravitational lensing.

In figure 13 , the lower disk image wraps under the black hole's shadow and then swings inward, becoming very thin, then up over the shadow and back down and outward to close on itself. This entire image comes from light rays emitted by the disk's bottom face: the wide bottom portion of the image, from rays that originate behind the hole, and travel under the hole and back upward to the camera; the narrow top portion, from rays that originate on the disk's front underside and travel under the hole, upward on its back side, over its top, and down to the camera—making one full loop around the hole.

There is a third disk image whose bottom portion is barely visible near the shadow's edge. That third image consists of light emitted from the disk's top face, that travels around the hole once for the visible bottom part of the image, and one and a half times for the unresolved top part of the image.

In the remainder of this section 4 we deal with a moderately realistic accretion disk—but a disk created for Interstellar by Double Negative artists rather than created by solving astrophysical equations such as [ 32 ]. In appendix A.6 we give some details of how this and other Double Negative accretion disk images were created. This artists' Interstellar disk was chosen to be very anemic compared to the disks that astronomers see around black holes and that astrophysicists model—so the humans who travel near it will not get fried by x-rays and gamma-rays. It is physically thin and marginally optically thick and lies in the black hole's equatorial plane. It is not currently accreting onto the black hole, and it has cooled to a position-independent temperature T = 4500 K, at which it emits a black-body spectrum.

4.1.2. Colour and brightness changes due to frequency shifts

The influences of Doppler and gravitational frequency shifts on the appearance of this disk are shown in figures 15 (b) and (c).

In figure 15 (b), we have turned on the colour changes, but not the corresponding brightness changes. As expected, the disk has become blue on the left and red on the right.

In figure 15 (c), we have turned on both the colour and the brightness changes. Notice that the disk's left side, moving toward the camera, has become very bright, while the right side, moving away, has become very dim. This is similar to astrophysically observed jets, emerging from distant galaxies and quasars; one jet, moving toward Earth is typically bright, while the other, moving away, is often too dim to be seen.

4.2. Lens flare and the accretion disk in the movie Interstellar

Christopher Nolan, the director and co-writer of Interstellar , and Paul Franklin, the visual effects supervisor, were committed to make the film as scientifically accurate as possible—within constraints of not confusing his mass audience unduly and using images that are exciting and fresh. A fully realistic accretion disk, figure 15 (c), that is exceedingly lopsided, with the hole's shadow barely discernible, was obviously unacceptable.

The first image in figure 15 , the one without frequency shifts and associated colour and brightness changes, was particularly appealing, but it lacked one element of realism that few astrophysicists would ever think of (though astronomers take it into account when modelling their own optical instruments). Movie audiences are accustomed to seeing scenes filmed through a real camera—a camera whose optics scatter and diffract the incoming light, producing what is called lens flare . As is conventional for movies (so that computer generated images will have visual continuity with images shot by real cameras), Nolan and Franklin asked that simulated lens flare be imposed on the accretion-disk image. The result, for the first image in figure 15 , is figure 16 .

Figure 16.  The accretion disk of figure 15 (a) (no colour or brightness shifts) with lens flare added—a type of lens flare called a 'veiling flare', which has the look of a soft glow and is very characteristic of IMAX camera lenses. This is a variant of the accretion disk seen in Interstellar . (Figure created by our Double Negative team using DNGR, and TM  & © Warner Bros. Entertainment Inc. (s15)). This image may be used under the terms of the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 (CC BY-NC-ND 3.0) license. Any further distribution of these images must maintain attribution to the author(s) and the title of the work, journal citation and DOI. You may not use the images for commercial purposes and if you remix, transform or build upon the images, you may not distribute the modified images.

This, with some embellishments, is the accretion disk seen around the black hole Gargantua in Interstellar .

All of the black-hole and accretion-disk images in Interstellar were generated using DNGR, with a single exception: when Cooper (Matthew McConaughey), riding in the Ranger spacecraft, has plunged into the black hole Gargantua, the camera, looking back upward from inside the event horizon, sees the gravitationally distorted external Universe within the accretion disk and the black-hole shadow outside it—as general relativity predicts. Because DNGR uses Boyer–Lindquist coordinates, which do not extend smoothly through the horizon, this exceptional image had to be constructed by Double Negative artists manipulating DNGR images by hand.

4.3. Some details of the DNGR accretion-disk simulations

4.3.1. simulating lens flare.

In 2002 one of our authors (James) formulated and perfected the following (rather obvious) method for applying lens flare to images. The appearance of a distant star on a camera's focal plane is mainly determined by the point spread function of the camera's optics. For Christopher Nolan's films we measure the point spread function by recording with HDR photography (see e.g. [ 46 ]) a point source of light with the full set of 35 and 65 mm lenses typically used in his IMAX and anamorphic cameras, attached to a single lens reflex camera. We apply the camera's lens flare to an image by convolving it with this point spread function. (For these optics concepts see, e.g. [ 47 ].) For the image 15 (a), this produces figure 16 . More recent work [ 48 ] does a more thorough analysis of reflections between the optical elements in a lens, but requires detailed knowledge of each lens' construction, which was not readily available for our Interstellar work.

4.3.2. Modelling the accretion disk for Interstellar

As discussed above, the accretion disk in Interstellar was an artist's conception, informed by images that astrophysicists have produced, rather than computed directly from astrophysicists' accretion-disk equations such as [ 32 ].

In our work on Interstellar , we developed three different types of disk models:

• an infinitely thin, planar disk, with colour and optical thickness defined by an artist's image;
• a three-dimensional 'voxel' model;
• for close-up shots, a disk with detailed texture added by modifying a commercial renderer, Mantra [ 49 ].

We discuss these briefly in appendix A.6 .

5. Conclusion

In this paper we have described the code DNGR, developed at Double Negative Ltd, for creating general relativistically correct images of black holes and their accretion disks. We have described our use of DNGR to generate the accretion-disk images seen in the movie Interstellar , and to explain effects that influence the disk's appearance: light-ray bending, Doppler and gravitational frequency shifts, shift-induced colour and brightness changes, and camera lens flare.

We have also used DNGR to explore, for a camera orbiting a fast spinning black hole, the gravitational lensing of a star field on the celestial sphere—including the lensing's caustics and critical curves, and how they influence the stellar images' pattern on the camera's sky, the creation and annihilation of image pairs, and the image motions.

Elsewhere [ 50 ], we describe our use of DNGR to explore gravitational lensing by hypothetical wormholes; particularly, the influence of a wormhole's length and shape on its lensing of stars and nebulae; and we describe the choices of length and shape that were made for Interstellar 's wormhole and how we generated that movie's wormhole images.

Acknowledgments

For very helpful advice during the development of DNGR and/or during the research with it reported here, we thank C Nolan, A Riazuelo, J-P Luminet, R Blandford, A Bohn, F Hebert, W Throwe, A Broderick and D Psaltis. For contributions to DNGR and its applications, we thank members of the Double Negative R & D team S Dieckmann, S Pabst, S Christopher, P-G Roberts, and D Maupu; and also Double Negative artists F Zangla, S Roth, Z Lord, I di Luigi, F Fan, N New, T Myles, and P Howlett. The construction of DNGR was funded by Warner Bros. Entertainment Inc., for generating visual effects for the movie Interstellar . We thank Warner Bros. for authorizing this code's additional use for scientific research, and in particular the research reported in this paper.

Appendix A.: Some details of DNGR

A.1. ray-tracing equations.

The foundations for our prescription are: (i) the Kerr metric written in Boyer–Lindquist coordinates 4

(ii) the 3 + 1 split of spacetime into space plus time embodied in this form of the metric; and (iii) the family of FIDOs whose world lines are orthogonal to the three-spaces of constant t , and their orthonormal basis vectors that lie in those three-spaces and are depicted in figure 1 ,

We shall also need three functions of r and of a ray's constants of motion b (axial angular momentum) and q (Carter constant), which appear in the ray's evolution equations ( A.15 ) below—i.e., in the equations for a null geodesic:

The prescription that we use, in DNGR, for computing the ray-tracing map and the blue shift is the following concrete embodiment of the discussion in section 2.1 .

A.2. Ray-bundle equations

Our prescription is a concrete embodiment of the discussion in section 2.2 ; it is a variant of the Sachs optical scalar equations [ 37 ]; and it is a slight modification of a prescription developed in the 1970s by Pineault and Roeder [ 35 , 36 ] 6 .

Our prescription relies on the following functions, which are defined along the reference ray. (a) The components of the ray bundle's four-momentum (wave vector) on the FIDO's orthonormal spherical basis

Here Q 1 , Q 2 , w , and S are given by

We shall state our prescription for computing the shape and orientation of the ray bundle on the celestial sphere separately, for two cases: a ray bundle that begins circular at the camera; and one that begins elliptical. Then, we shall briefly sketch the Pineault–Roeder [ 35 , 36 ] foundations for these prescriptions.

A.2.1. Circular ray bundle at camera

A.2.2. elliptical ray bundle at camera.

Our prescription, for a ray bundle that begins elliptical at the camera, is this:

• (v)   Continue and conclude with steps (ii) and (iii) of appendix A.2.1 .

A.2.3. Foundations for these ray-bundle prescriptions

For completeness we briefly describe the Pineault–Roeder [ 35 , 36 ] foundations for these ray-bundle-evolution prescriptions.

To describe the ray bundle and its evolution, (following Pineault and Roeder) we introduce two complex numbers (transverse vectors) ξ and η , whose real and imaginary parts are functions that are evolved by the ray-bundle equations ( A.23 ):

The outer edge of the ray bundle, at location ζ along the reference ray, is described by the complex number

By an argument similar to the first part of the paragraph before last, one can deduce that anywhere along the evolving ray bundle

and correspondingly that the minor angular diameter at the celestial sphere is the second of equations ( A.25 ).

A.3. Filtering

A.3.1. spatial filtering and how we handle point stars.

In DNGR we treat stars as point sources of light with infinitesimal angular size. We trace rays backwards from the camera to the celestial sphere. If we were to treat these rays as infinitely thin, there would be zero probability of any ray intersecting a star; so instead we construct a beam with a narrow but finite angular width, centred on a pixel on the camera's sky and extending over a small number of adjacent pixels, we evolve the shape of this beam along with the ray, and if the beam intercepts the star, we collect the star's light into it. This gives us some important benefits.

• The images of our unresolved stars remain small: they don't stretch when they get magnified by gravitational lensing.
• The fractional change in the beam's solid angle is directly related to the optical magnification due to gravitational lensing and hence to the intensity (brightness) change in the image of an unresolved star.
• When sampling images of accretion discs or extended structures such as interstellar dust clouds, we minimize moiré artefacts by adapting the resampling filter according to the shape of the beam [ 55 ].

Another consequence is that each star contributes intensity to several pixels. The eye is sensitive to the sum of these and as a single star crosses this grid, this sum can vary depending on the phase of the geometric image of the star on the grid 7 . This can cause distracting flickering of stars as they traverse the virtual camera's image plane. We mitigate this effect by modulating the star's intensity across the beam with a truncated Gaussian filter and by setting the beam's initial radius to twice the pixel separation.

With this filter, the sum is brightest when the geometric image of the star falls exactly on a pixel and dimmest when centred between four pixels. The shape and width of the filter are designed to give a maximum 2% difference between these extremes, which we found, empirically, was not noticeable in fast changing Interstellar scenes.

A.3.2. Temporal filtering: motion blur

For moving images, we need to filter over time as well as space. A traditional film camera typically exposes the film for half the time between individual frames of film, so for a typical 24 fps (frame per second) film, the exposure time will be 1/48 s. (This fraction is directly related to the camera's 'shutter angle': the shutters in film cameras are rotating discs with a slice cut out. The film is exposed when the slice is over the emulsion, and the film moves onto the next frame when covered. The most common shape is a semicircular disk which is a '180° shutter'.) Any movement of the object or camera during the exposure leads to motion blur. In our case, if the camera is orbiting a black hole, stellar images close to a critical curve appear to zip around in frantic arcs and would appear as streaks of light on a 1/48 s photograph. We aim to reproduce that effect when creating synthetic images for films.

This motion blur in computer graphics is typically simulated with Monte Carlo methods, computing multiple rays per pixel over the shutter duration. In order to cleanly depict these streaks with Monte Carlo methods, we would need to compute the paths of many additional rays and the computational cost of calculating each ray is very high. Instead, in DNGR we take an analytic approach to motion blur (cf figure A1 ) by calculating how the motion of the camera influences the motion of the deflected beam:

Figure A1.  Left-to-right: no motion blur; Monte Carlo motion blur with four time samples per-pixel; analytic motion blur. Relative computation time is approximately in the ratio 1:4:2. Lens flare has been added to each image to illustrate how these images would typically be seen in the context of a movie.

The camera's instantaneous position influences the beam's momentary state, and likewise the camera's motion affects the time derivatives of the beam's state. We augment our ray and ray bundle equations ( A.15 ) and ( A.23 ) to track these derivatives throughout the beam's trajectory and end up with a description of an elliptical beam being swept through space during the exposure. The beam takes the form of a swept ellipse when it reaches the celestial sphere, and we integrate the contributions of all stars within this to create the motion-blurred image 8 . These additional calculations approximately double the computation time, but this is considerably faster than a naive Monte Carlo implementation of comparable quality.

A.3.3. Formal description of our analytic approach to motion blur

We can put our analytic method into a more formal setting, using the mathematical description of motion blurred rendering of Sung et al [ 59 ], as follows. We introduce the quantity

Luckily, in Interstellar , the design of the shots meant this rarely happened: the main source of motion blur was the movement of the spaceship around the black hole, and not local camera motion.

To handle any cases where this approximation might cause a problem, we also implemented a hybrid method where we launch a small number of Monte Carlo rays over the shutter duration and each ray sweeps a correspondingly shorter analytic path.

We used a very similar technique for the accretion disk.

A.4. Implementation

DNGR was written in C++ as a command-line application. It takes as input the camera's position, velocity, and field of view, as well as the black hole's location, mass and spin, plus details of any accretion disk, star maps and nebulae.

Each of the 23 million pixels in an IMAX image defines a beam that is evolved as described in appendix A.2.

The beam's evolution is described by the set of coupled first and second order differential equations ( A.15 ) and ( A.23 ) that we put into fully first order form and then numerically integrate backwards in time using a custom implementation of the Runge–Kutta–Fehlberg method (see, e.g., chapter 7 of [ 57 ]). This method gives an estimate of the truncation error at every integration step so we can adapt the step size during integration: we take small steps when the beam is bending sharply relative to our coordinates, and large steps when it is bending least. We use empirically determined tolerances to control this behaviour. Evolving the beam along with its central ray triples the time per integration step, on average, compared to evolving only the central ray.

The beam either travels near the black hole and then heads off to the celestial sphere; or it goes into the black hole and is never seen again; or it strikes the accretion disk, in which case it gets attenuated by the disk's optical thickness to extinction or continues through and beyond the disk to pick up additional data from other light sources, but with attenuated amplitude. We use automatic differentiation [ 58 ] to track the derivatives of the camera motion through the ray equations.

Each pixel can be calculated independently, so we run the calculations in parallel over multiple CPU cores and over multiple computers on our render-farm.

We use the OpenVDB library [ 60 ] to store and navigate volumetric data and Autodesk's Maya [ 61 ] to design the motion of the camera. (The motion is chosen to fit the film's narrative.) A custom plug-in running within Maya creates the command line parameters for each frame. These commands are queued up on our render-farm for off-line processing.

A.5. DNGR code characteristics and the Double Negative render-farm

A typical IMAX image has 23 million pixels, and for Interstellar we had to generate many thousand images, so DNGR had to be very efficient. It has 40 000 lines of C++ code and runs across Double Negative's Linux-based render-farm. Depending on the degree of gravitational lensing in an image 9 , it typically takes from 30 min to several hours running on ten CPU cores to create a single IMAX image. The longest renders were those of the close-up accretion disk when we shoe-horned DNGR into Mantra. For Interstellar , render times were never a serious enough issue to influence shot composition or action.

Our London render-farm comprises 1633 Dell-M620 blade servers; each blade has two ten-core E5-2680 Intel Xeon CPUs with 156 GB RAM. During production of Interstellar , several hundred of these were typically being used by our DNGR code.

A.6. DNGR modelling of accretion disks

Our code DNGR includes three different implementations of an accretion disk.

Thin disk : for this, we adapted our DNGR ray-bundle code so it detects intersections of the beam with the disk. At each intersection, we sample the artist's image in the manner described in section 2.2 and appendix A.3 above, to determine the colour and intensity of the bundle's light and we attenuate the beam by the optical thickness (cf appendix A.4).

Volumetric disk : the volumetric accretion disk was built by an artist using SideFX Houdini software and stored in a volumetric data structure containing roughly 17 million voxels (a fairly typical number). Each voxel describes the optical density and colour of the disk in that region.

We used extinction-based sampling [ 62 ] to build a mipmap volume representation of this data. The length of the ray bundle was split into short piecewise-linear segments which, in turn, were traced through the voxels. We used the length of the major axis of the beam's cross section to select the closest two levels in the mipmap volume; and in each level we sampled the volume data at steps the length of a voxel, picking up contributions from the colour at each voxel and attenuating the beam by the optical thickness. The results from the two mipmap levels were interpolated before moving on to the next line segment.

Close-up disk with procedural textures : Side Effects Software's renderer, Mantra, has a plug-in architecture that lets you modify its operation. We embedded the DNGR ray-tracing code into a plug-in and used it to generate piecewise-linear ray segments which were evaluated through Mantra. This let us take advantage of Mantra's procedural textures 10 and shading language to create a model of the accretion disk with much more detail than was possible with the limited resolution of a voxelized representation. However this method was much slower so was only used when absolutely necessary.

Disk layers close to the camera : the accretion-disk images in Interstellar were generated in layers that were blended together to form the final images. Occasionally a layer only occupied space in the immediate vicinity of the camera, so close that the infuences of spacetime curvature and gravitational redshifts were negligible. These nearby layers were rendered as if they were in flat spacetime, to reduce computation time.

We set the white balance of our virtual camera to render a 6500 K blackbody spectrum with equal red, green and blue pixel values by applying a simple gain to each colour channel. We did not model the complex, nonlinear interaction between the colour-sensitive layers that occurs in real film.

A.7. Comparison of DNGR with astrophysical codes and with film-industry CGI codes

Near the end of section 1.1 , we compared our code DNGR with the state-of-the-art astrophysical visualization code GRay. The most important differences—DNGR's use of light-beam mappings versus GRay's use of individual-ray mappings, and DNGR's use of ordinary processors versus GRay's use of GPUs—were motivated by our different goals: smoothness of images in movies versus fast throughput in astrophysics.

In appendix A.3.1 we have described our methods of imaging star fields, using stars that are point sources of light: we feed each star's light into every light beam that intersects the star's location, with an appropriate weighting.

Other gravitational-lensing codes deal with star fields differently. For example, Müller and Frauendiener [ 29 ] calculate where each point-star ends up in the camera's image plane, effectively producing the inverse of the traditional ray-tracing algorithm. They do this for lensing by a non-spinning black hole (Schwarzchild metric) which has a high degree of symmetry, making this calculation tractable. Doing so for a spinning black hole would be much more challenging.

A common method for rendering a star-field is to create a 2D source picture (environment map) that records the stars' positions as finite-sized dots in the source plane (see e.g. [ 64 ]). This source picture is then sampled using the evolved rays from the camera. This has the disadvantage that stars can get stretched in an unrealistic way in areas of extreme magnification, such as near the critical curves described in section 3.3.1 of this paper. As we discussed in appendix A.3.1 , our DNGR light-beam technique with point stars circumvents this problem—as does the Müller-Frauendiener technique with point stars.

We also have done such simulations but not in enough detail to reveal much new.

Our choice of Boyer–Lindquist coordinates prevents the camera from descending into the black hole. For that, it is not hard to switch to ingoing Kerr coordinates; but if one wants to descend even further, across an inner (Cauchy) horizon of the maximally extended Kerr spacetime, one must then switch again, e.g., to outgoing Kerr coordinates. Riazuelo [ 42 ] has created an implementation of the ray tracing equations that does such multiple switches. As a foundation for Interstellar , Thorne did so but only for the switch to ingoing Kerr coordinates, as Interstellar assumes the inner horizons have been replaced by the Marolf–Ori shock singularity [ 51 ] and the Poisson–Israel mass-inflation singularity [ 52 ]; see chapters 24 and 26 of [ 40 ].

These are the super-Hamiltonian variant of the null geodesic equations; see, e.g., section 33.5 of [ 33 ] or appendix A of [ 54 ].

The same is true, of course, for each bit of a nebula or accretion disk. We discuss some details of how DNGR handles accretion disks in appendix A.6.

We took a similar approach when motion-blurring the accretion disks discussed in appendix A.6.

More specifically: the render time depends mainly on the number of steps in the integration. This, in turn, depends on the truncation errors in the integration scheme. The tolerances are tighter on the position of the ray than its shape, as errors in position give rise to more noticeable artefacts. Empirically, renders of regions close to the black hole's shadow are much slower than any other.

A procedural texture uses an algorithm, such as fractal noise, to generate detail at arbitrary resolution, unlike a texture based on an image file, which has a finite resolution.

Movie 1. (42 MB, MP4) View of a starfield under the influence of gravitational lensing. The camera is at radius r=2.6 GM/c2

Movie 2. (112 MB, MP4) View of a starfield under the influence of gravitational lensing. The camera is at radius r=6.03 GM/c2

Movie 3. (185 MB, MP4) View of a starfield under the influence of gravitational lensing. The camera is at radius r=6.03 GM/c2. The primary and secondary critical curves are overlaid in purple and the path of a star at polar angle 0.608 pi is overlaid in red.

Movie 4. (540 KB, MP4) For a camera at radius rc = 6.03 GM/c2: Animation showing the mapping between points on the primary critical curve in the camera's sky and the primary caustic curve on the celestial sphere.

Movie 5. (456 KB, MP4) For a camera at radius rc = 6.03 GM/c2: Animation showing the mapping between points on the secondary critical curve in the camera's sky and the secondary caustic curve on the celestial sphere.

Movie 6. (948 KB, MP4) For a camera at radius rc = 2.6 GM/c2: Animation showing the mapping between points on the primary critical curve in the camera's sky and the primary caustic curve on the celestial sphere.

Movie 7. (831 KB, MP4) For a camera at radius rc = 2.6 GM/c2: Animation showing the mapping between points on the secondary critical curve in the camera's sky and the secondary caustic curve on the celestial sphere.

Movie 8. (1.53 MB, MP4) For a camera at radius rc = 2.6 GM/c2: Animation showing the mapping between points on the tertiary critical curve in the camera's sky and the tertiary caustic curve on the celestial sphere.

May 17, 2024

How Can You ‘See’ a Black Hole?

How do astronomers find the darkest objects in the universe?

By Phil Plait

An illustration of the black hole Cygnus X-1, the first ever glimpsed by astronomers. The stellar-mass black hole (right) siphons gas from its companion, a blue supergiant star (left). This material forms a whirling, glowing accretion disk around the black hole, revealing the dark object’s presence.

NASA, ESA, Martin Kornmesser (ESA/Hubble) ( CC BY 4.0 )

Imagine an object with gravity so powerful that nothing, not even light, can escape after falling in. Such a beast would be like an infinitely deep hole and utterly black .

Someone should come up with a catchy name for it.

Black holes are probably the most popular astronomical objects among the public. Whenever I give talks, the audience peppers me with questions about them even when my topic is something completely different. People love a good monster story, and black holes are the scariest of them all.

On supporting science journalism

If you're enjoying this article, consider supporting our award-winning journalism by subscribing . By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.

They were just a hypothesis for a long time. Then, in the 1960s, astrophysicists found the first direct evidence of a black hole , which lurked relatively nearby within the Milky Way. But how do you find something if, by definition, it’s effectively invisible?

Surprisingly, there are lots of ways to uncover these voracious objects. And ironically, the very thing that makes them so dark—their gravity—is what betrays their presence.

Our first glimpse of a black hole came in 1964 via two small suborbital sounding rockets that were launched to survey and map x-ray sources across most of the sky. One of these sources, located in the constellation of Cygnus, was quite powerful and appeared in many follow-up observations. Astronomers dubbed it Cygnus X-1 because it was the first x-ray source found in that constellation. As observations improved, astronomers could pinpoint this source in the sky, revealing a bright star at its location some 7,000 light-years from Earth. Even though this star was massive and luminous, it had nowhere near the wherewithal to emit x-rays at the amount detected. All that radiation was coming from something else.

Theories predicted the source must be a black hole. If one orbits a star closely, its ridiculously strong gravity can draw in matter from that star. This material spirals into the black hole and does eventually fall in. But first it forms a flat disk called an accretion disk just above the black hole’s point of no return—the boundary, called an event horizon, beyond which not even light can escape. Matter orbiting nearer to the black hole moves more rapidly—close to the speed of light!—while matter farther out moves more slowly. As the material in the disk rubs against itself, it generates a vast amount of friction, heating up to millions of degrees. Hot material glows, and this stuff is hellishly hot, so it emits copious amounts of light. We can see that light, not so incidentally, because it’s emitted outside the black hole’s event horizon.

That emission includes x-rays, which are just a high-energy form of light . The actual physics are dauntingly complex , involving swirling magnetic fields of incredible strength, but in the end, just above the black hole’s event horizon, that matter can blast out x-rays. This was—and still is—considered extremely strong evidence for Cygnus X-1 being a black hole.

Further study of the massive star in its location supported that conclusion as well: research revealed that the star was in a tight orbit with a massive object, something that had around 20 times the mass of our sun yet emitted no light. A star that was so massive would be incredibly luminous, so whatever the companion was, it was dark. Hence, it was a black hole. (It’s weird and rather fun that one piece of evidence for the existence of black holes is when we don’t see them.)

Around the same time Cygnus X-1 was shown to be a stellar-mass black hole, astronomers were also finding objects that were much more distant, some billions of light-years away, yet still so bright that they initially were mistaken for stars. Such “quasi-stellar objects,” or quasars, must be phenomenally luminous to be seen at all from so far off. Astronomers eventually realized quasars had to be powered by enormous black holes, each with a mass that was millions or even billions of times that of the sun. Huge amounts of material were flowing into them, creating immense, glowing accretion disks so bright that they could be seen from across the universe. We now know that almost all big galaxies have such a supermassive black hole in their center— the Milky Way’s is called Sagittarius A*, or Sgr A* , and is about four million solar masses—and that these objects profoundly affect the birth and growth of whole galaxies. Very few are now eating enough material to become a glowing quasar, but enough do that we see millions of such “active” galaxies across the cosmos.

Yet black holes don’t need to announce their existence so flamboyantly. Some stellar-mass black holes reside in wider orbits with their companion star and aren’t accreting material. Even in these cases, painstaking measurements can reveal the companion star’s motion as it circles the compact, dark object. This is very difficult to detect, however, and only a few black holes have been found that way. Using data on stellar motions from the European Space Agency’s Gaia spacecraft, astronomers recently found one that’s only 2,000 light-years from Earth . Presumably, black holes that are even closer to us are out there, too, as yet unseen. We’re probably not in any danger—the odds of encountering one adrift in the Milky Way are extremely long. But there are likely tens of millions of such quiescent black holes in our galaxy alone.

Sometimes a black hole doesn’t have to be physically near any other objects to reveal its presence either. One of Albert Einstein’s brilliant ideas was that gravity warps space , and light has to follow that distorted path like a truck driving down a curving road. Light passing through the powerful gravitational field of a black hole can be wildly distorted, an effect called strong gravitational lensing . Astronomers have recently used this method to discover and weigh a supermassive black hole tipping the cosmic scale at more than 30 billion solar masses in a galaxy nearly three billion light-years away . It happens to lie almost exactly in the same direction as a much more distant galaxy, and the distortion in that background galaxy’s light revealed the black hole’s presence and immense mass.

In a related Einstein-predicted effect, when two black holes collide, they can send out powerful ripples in the fabric of spacetime called gravitational waves . Many massive stars are born in binary systems, and each of the two stars in such systems can in turn explode as a supernova, leaving behind a black hole. Over time, the two compact objects spiral together until they merge in a colossal blast of gravitational waves. These were first detected in 2015 , and we’ve now seen well more than 100 such events . A European Space Agency mission called the Laser Interferometer Space Antenna , or LISA, is designed to detect giant gravitational waves, including those from the mergers of supermassive black holes that are thought to occur after whole galaxies collide. And LISA may find hundreds of such events after its projected launch date in the mid-2030s.

Our understanding of black holes went from considering them to be purely hypothetical to seeing them everywhere pretty rapidly. We now know they play critical roles in the evolution of stars and galaxies, yet we still have more questions than answers. How do they form? How did supermassive black holes get so big so rapidly at the dawn of the universe ? Can they die ?

Black holes can hide, but honestly, in a lot of cases, they’re just not very good at it. We can spot them, and the more we do, the more answers we can find.

Suggested Searches

• Climate Change
• Expedition 64
• Mars perseverance
• SpaceX Crew-2
• International Space Station
• View All Topics A-Z

Humans in Space

Earth & climate, the solar system.

• The Universe

Aeronautics

Learning resources, news & events.

How NASA Tracked the Most Intense Solar Storm in Decades

NASA’s X-59 Passes Milestone Toward Safe First Flight 

5 Things to Know About NASA’s Tiny Twin Polar Satellites

• Search All NASA Missions
• A to Z List of Missions
• Upcoming Launches and Landings
• Spaceships and Rockets
• Communicating with Missions
• James Webb Space Telescope
• Hubble Space Telescope
• Why Go to Space
• Astronauts Home
• Commercial Space
• Destinations
• Living in Space
• Explore Earth Science
• Earth, Our Planet
• Earth Science in Action
• Earth Multimedia
• Earth Science Researchers
• Pluto & Dwarf Planets
• Asteroids, Comets & Meteors
• The Kuiper Belt
• The Oort Cloud
• Skywatching
• The Search for Life in the Universe
• Black Holes
• The Big Bang
• Dark Energy & Dark Matter
• Earth Science
• Planetary Science
• Astrophysics & Space Science
• The Sun & Heliophysics
• Biological & Physical Sciences
• Lunar Science
• Citizen Science
• Astromaterials
• Aeronautics Research
• Human Space Travel Research
• Science in the Air
• NASA Aircraft
• Flight Innovation
• Supersonic Flight
• Air Traffic Solutions
• Green Aviation Tech
• Drones & You
• Technology Transfer & Spinoffs
• Space Travel Technology
• Technology Living in Space
• Manufacturing and Materials
• Science Instruments
• For Kids and Students
• For Educators
• For Colleges and Universities
• For Professionals
• Science for Everyone
• Requests for Exhibits, Artifacts, or Speakers
• STEM Engagement at NASA
• NASA's Impacts
• Centers and Facilities
• Directorates
• Organizations
• People of NASA
• Internships
• Our History
• Doing Business with NASA
• Get Involved
• Aeronáutica
• Ciencias Terrestres
• Sistema Solar
• All NASA News
• Video Series on NASA+
• Newsletters
• Social Media
• Media Resources
• Upcoming Launches & Landings
• Virtual Events
• Sounds and Ringtones
• Interactives
• STEM Multimedia

Hubble Views Cosmic Dust Lanes

Eleasa Kim: Pioneering CLDP Payload Operations and Cultural Integration

NASA Tests Technology, Practices Artemis Moonwalks in Arizona Desert

Station Science 101 | Research in Microgravity: Higher, Faster, Longer

How ‘Glowing’ Plants Could Help Scientists Predict Flash Drought

NASA Teammates Recall Favorite Memories Aboard Flying Laboratory

NASA’s Juno Provides High-Definition Views of Europa’s Icy Shell

The Next Full Moon is the Flower, Corn, or Corn Planting Moon

Binoculars: A Great First Telescope

Discovery Alert: An Earth-sized World and Its Ultra-cool Star

Hubble Views the Dawn of a Sun-like Star 

Amendment 16: New Opportunity: B.22 Artificial Intelligence Applications in Heliophysics

Amendment 15: New Opportunity: E.11 Consortium in Biological Sciences

NASA to Start Designing More Sustainable Jet Engine Core

Aviary: A New NASA Software Platform for Aircraft Modelling

Tech Today: A NASA-Inspired Bike Helmet with Aerodynamics of a Jet  

Tech Today: NASA’s Ion Thruster Knowhow Keeps Satellites Flying

NASA Selects Commercial Service Studies to Enable Mars Robotic Science

NASA Challenge Gives Artemis Generation Coders a Chance to Shine

NASA Around the World: Interns Teach Virtual Lessons in Kenya

NASA Names Deputy Station Manager, Operations Integration Manager

Meet NASA Women Behind World’s Largest Flying Laboratory

Diez maneras en que los estudiantes pueden prepararse para ser astronautas

Astronauta de la NASA Marcos Berríos

Resultados científicos revolucionarios en la estación espacial de 2023

How nasa’s roman mission will hunt for primordial black holes.

Ashley Balzer

Astronomers have discovered black holes ranging from a few times the Sun’s mass to tens of billions. Now a group of scientists has predicted that NASA’s Nancy Grace Roman Space Telescope could find a class of “featherweight” black holes that has so far eluded detection.

Today, black holes form either when a massive star collapses or when heavy objects merge. However, scientists suspect that smaller “primordial” black holes, including some with masses similar to Earth’s, could have formed in the first chaotic moments of the early universe.

“Detecting a population of Earth-mass primordial black holes would be an incredible step for both astronomy and particle physics because these objects can’t be formed by any known physical process,” said William DeRocco, a postdoctoral researcher at the University of California Santa Cruz who led a study about how Roman could reveal them. A paper describing the results has been published in the journal Physical Review D. “If we find them, it will shake up the field of theoretical physics.”

Primordial Black Hole Recipe

The smallest black holes that form nowadays are born when a massive star runs out of fuel. Its outward pressure wanes as nuclear fusion dies down, so inward gravitational pull wins the tug-of-war. The star contracts and may get so dense it becomes a black hole.

But there’s a minimum mass required: at least eight times that of our Sun. Lighter stars will either become white dwarfs or neutron stars .

Conditions in the very early universe, however, may have allowed far lighter black holes to form. One weighing the mass of Earth would have an event horizon –– the point of no return for infalling objects –– about as wide as a U.S. dime coin.

Just as the universe was being born, scientists think it experienced a brief but intense phase known as inflation when space expanded faster than the speed of light. In these special conditions, areas that were denser than their surroundings may have collapsed to form low-mass primordial black holes.

While theory predicts the smallest ones should evaporate before the universe has reached its current age, those with masses similar to Earth could have survived.

Discovering these tiny objects would have an enormous impact on physics and astronomy.

“It would affect everything from galaxy formation to the universe’s dark matter content to cosmic history,” said Kailash Sahu, an astronomer at the Space Telescope Science Institute in Baltimore, who was not involved in the study. “Confirming their identities will be hard work and astronomers will need a lot of convincing, but it would be well worth it.”

Hints of Hidden Homesteaders

Observations have already revealed clues that such objects may be lurking in our galaxy. Primordial black holes would be invisible, but wrinkles in space-time have helped round up some possible suspects.

Microlensing is an observational effect that occurs because the presence of mass warps the fabric of space-time, like the imprint a bowling ball makes when set on a trampoline. Any time an intervening object appears to drift near a background star from our vantage point, the star’s light must traverse the warped space-time around the object. If the alignment is especially close, the object can act like a natural lens, focusing and amplifying the background star’s light.

Separate groups of astronomers using data from MOA (Microlensing Observations in Astrophysics) –– a collaboration that conducts microlensing observations using the Mount John University Observatory in New Zealand –– and OGLE (the Optical Gravitational Lensing Experiment) have found an unexpectedly large population of isolated Earth-mass objects .

Planet formation and evolution theories predict certain masses and abundances of rogue planets ––worlds roaming the galaxy untethered to a star. The MOA and OGLE observations suggest there are more Earth-mass objects drifting through the galaxy than models predict.

“There’s no way to tell between Earth-mass black holes and rogue planets on a case-by-case basis,” DeRocco said. But scientists expect Roman to find 10 times as many objects in this mass range than ground-based telescopes. “Roman will be extremely powerful in differentiating between the two statistically.”

DeRocco led an effort to determine how many rogue planets should be in that mass range, and how many primordial black holes Roman could discern amongst them.

Finding primordial black holes would reveal new information about the very early universe, and would strongly suggest that an early period of inflation did indeed occur. It could also explain a small percentage of the mysterious dark matter scientists say makes up the bulk of our universe’s mass, but have so far been unable to identify.

“This is an exciting example of something extra scientists could do with data Roman is already going to get as it searches for planets,” Sahu said. “And the results are interesting whether or not scientists find evidence that Earth-mass black holes exist. It would strengthen our understanding of the universe in either case.”

The Nancy Grace Roman Space Telescope is managed at NASA’s Goddard Space Flight Center in Greenbelt, Maryland, with participation by NASA’s Jet Propulsion Laboratory and Caltech/IPAC in Southern California, the Space Telescope Science Institute in Baltimore, and a science team comprising scientists from various research institutions. The primary industrial partners are BAE Systems, Inc in Boulder, Colorado; L3Harris Technologies in Rochester, New York; and Teledyne Scientific & Imaging in Thousand Oaks, California.

Download high-resolution video and images from NASA’s Scientific Visualization Studio

By Ashley Balzer NASA’s Goddard Space Flight Center , Greenbelt, Md.

Media Contact: Claire Andreoli 301-286-1940 [email protected] NASA’s Goddard Space Flight Center, Greenbelt, Md.

Explore More

How NASA’s Roman Space Telescope Will Uncover Lonesome Black Holes

Why NASA’s Roman Mission Will Study Milky Way’s Flickering Lights

WFIRST Will Add Pieces to the Dark Matter Puzzle

Related terms.

• Nancy Grace Roman Space Telescope
• Astrophysics
• Dark Matter
• Galaxies, Stars, & Black Holes
• Galaxies, Stars, & Black Holes Research
• Goddard Space Flight Center
• Origin & Evolution of the Universe
• Science & Research

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Proc Natl Acad Sci U S A
• v.98(19); 2001 Sep 11

Black holes

B. brügmann.

* Max Planck Institute for Gravitational Physics, Albert Einstein Institute, Am Mühlenberg 1, 14476 Golm, Germany; ‡ University of California, Los Angeles, CA 90095-1562; and § Astrophysical Institute Potsdam, An der Sternwarte 16, 14482, Potsdam, Germany

Recent progress in black hole research is illustrated by three examples. We discuss the observational challenges that were met to show that a supermassive black hole exists at the center of our galaxy. Stellar-size black holes have been studied in x-ray binaries and microquasars. Finally, numerical simulations have become possible for the merger of black hole binaries.

Black holes are a striking example of a prediction of Einstein's theory of gravity, general relativity. Although it took many decades before the physical concept of a black hole was fully understood and widely accepted, recent years have seen rapid advances on both the observational and theoretical side, which we want to illustrate in this brief note with three examples. Black holes have become an astrophysical reality. Solid observational evidence exists for black holes in two mass ranges. Supermassive black holes of 10 6 -10 9 solar masses have been observed at the centers of many galaxies, and here we discuss the observational challenges that were met to show that there exists a black hole at the center of our own galaxy. Stellar-size black holes of about 3–20 solar masses have been studied in x-ray binaries and microquasars. Finally, numerical simulations have become possible for the merger of black hole binaries.

Recent high-resolution imaging studies of stars at the center of our Galaxy have produced strong dynamical evidence for a central concentration of dark matter, establishing the Milky Way as the most convincing case of a galaxy containing a central supermassive black hole ( 1 , 2 ). In those experiments, images obtained over 2–6 years at the Keck telescope ( 1 ) and European Southern Observatory's New Technology Telescope ( 2 ) provided measurements of the stars' velocities in the plane of the sky, from which a statistical analysis revealed the existence of 2−3 × 10 6 solar masses of dark matter contained within a radius of 0.015 parsec (1 parsec = 3.09 × 10 16 m), or 2.6 light weeks. At this meeting, new results from the Keck telescope were reported. With this new data set, which triples the number of maps obtained and doubles the time baseline for the Keck experiment, the velocity uncertainties are reduced by a factor of 3 compared with the earlier Keck work ( 1 ), primarily as a result of the increased time baseline and, in the central square arcsecond, by a factor of 6 compared with ref. 2 , due to the higher angular resolution (0."05 vs. 0."15). In addition to simply increasing the time baseline for velocity measurements, the new measurements have advanced this experiment in two significant ways: ( i ) the first Keck adaptive optics (AO) images of the galactic center have been obtained (Fig. ​ (Fig.1), 1 ), allowing a more complete census of stars in this region to be obtained ( 3 ), and ( ii ) the first measurements of stellar accelerations in this field have now been achieved ( 4 ).

A ≈3" × 3" region showing the Sgr A* cluster (the faint stars located just to the right of the center of the field of view). Both images were taken in May 1999 at 2.2 μm (K-band); however, the image on the left was produced by shift-and-adding Keck I speckle data, and the image on the right was obtained with the new Keck II adaptive optics system. The adaptive optics image represents a large improvement.

With longer integration times, AO should probe a yet larger sample of fainter stars, place stringent limits on Sgr A*, and explore the possibility of a gravitational lensing experiment ( 5 ). For the time being, the AO map has increased the number of stars in the proper motion study ( 3 ). With relative positional accuracies of ≈3 milliarcseconds, the motions of stars are now fit with a second-order polynomial as opposed to a simple linear fit, which was done in earlier work. Among the 90 stars in the original Keck proper motion sample ( 1 ), accelerations of 2–5 milliarseconds/yr 2 , or equivalently 3–6 × 10 −6 km/sec 2 , are now detected for three stars, S0–1, S0–2, and S0–4 ( 4 ). These three stars are independently distinguished in this sample as being among the fastest moving stars ( v = 565 to 1,383 km/sec) and among the closest to the nominal position of Sgr A* (< r > = 0.003 to 0.015 parsec). Acceleration vectors, in principle, are more precise tools than velocity vectors for studying the properties of the central dark mass. These acceleration measurements improve the localization of our Galaxy's dynamical center by a factor of 3, which is critical for reliably associating any near-infrared source with the black hole, given the complexity of the region. In addition, these acceleration measurements increase the minimum mass density inferred by a factor of 8 over previous results, thereby strengthening the case for a black hole.

X-Ray Binaries and Microquasars.

In contrast to the need for measuring dozens of stars to determine the mass of the black hole in the Galactic Center, that of black holes in x-ray binary systems can be deduced either from optical/IR measurements of just one star, namely the companion of the stellar-mass black hole, or from x-ray observations of the binary. In x-ray binaries, a black hole of typically 3–10 solar masses and a normal star (1–30 solar masses) orbit each other. Matter is pulled off the companion star and, because of its angular momentum, is forming an accretion disk as it moves toward the black hole. Before finally falling into the black hole, the matter heats up to several million degrees at the inner part of the disk and emits luminous x-ray radiation. Because the whole accretion process is highly variable, numerous such black hole binaries have been found over the last decade, thanks to x-ray detectors on satellites, such as Compton Gamma-Ray Observatory and Rossi X-Ray Timing Explorer, constantly monitoring the whole sky.

Although optical/IR spectroscopic measurements of the velocity of the companion star can readily determine the mass of the black hole, x-ray measurements promise to be a sharper and even more flexible diagnostic tool as they reach down to the inner edge of the accretion disk at a few Schwarzschild radii of the black hole. High time-resolution observations of black hole binaries have revealed quasiperiodic oscillations in x-ray emission at a stable minimum period, e.g., at 67 Hz for GRS 1915 + 105 ( 6 ), which may very well be related to the period of the innermost stable orbit of the accretion disk. The Kerr metric fixes this period as a function of mass and spin of the black hole. Because the maximum temperature of the innermost disk, as discernable from x-ray spectroscopy, is also thought to be just a function of black hole mass and spin, detailed x-ray observations can be used to determine both the mass AND spin of a black hole ( 7 ).

A small fraction of black hole binaries also eject matter at relativistic speeds into two opposite jets that are observable in the radio band as knots moving apart at superluminal speed. Actually, GRS 1915 + 105 is the most famous representative of this class of object, called microquasars ( 8 ). Simultaneous observations of these microquasars in the x-ray, optical/IR, and radio band have for the first time revealed a relation between accretion disk instabilities and jet ejections ( 9 , 10 ). Theorists now face the challenge of modeling the highly dynamical processes of nonsteady accretion and jet formation, acceleration, and collimation, with all of the complications of three-dimensional magnetohydrodynamics and general relativity.

Another example in which the full Einstein equations have to be solved in the highly dynamic and nonlinear regime is the collision and merger of two black holes. In fact, although single black holes are comparatively simple exact solutions of the Einstein equations, the two-body problem of general relativity for black holes, or neutron stars, is unsolved. As opposed to Newtonian theory, where the Kepler ellipses provide an astrophysically relevant example for the analytic solution of the two-body problem, in Einsteinian gravity there are no corresponding exact solutions. The failure of Einstein's theory to lead to stable orbits is due to the fact that, in general, two orbiting bodies will emit gravitational waves that carry away energy and momentum from the system, leading to an inspiral. Of course, this “leak” is not considered detrimental. It is expected that gravitational wave astronomy will open a new window onto the universe ( 11 ), and binary black hole mergers are considered to be among the most likely candidates for first detection.

Numerical relativity is only now approaching a state where the evolution of rather general three-dimensional data sets can be simulated on a computer to solve the Einstein equations (see, e.g., ref. 12 ). After early computations for the axisymmetric head-on collision of two black holes in the 1970s, it was in 1995 that, for the first time, spherically symmetric data for a single Schwarzschild black hole was evolved with a three-dimensional computer code ( 13 ). The first fully three-dimensional binary black hole evolutions, the grazing collision of nearby spinning and moving black holes, is reported in ref. 14 . Fig. ​ Fig.2 2 shows a visualization of such a black hole merger [M. Alcubierre, W. Benger, B. Brügmann, G. Lanfermann, L. Nerger, E. Seidel & R. Takahashi, R. http://jean-luc.aei.mpg.de/Press/BH1999/ ]. These simulations are still severely limited in achievable evolution time (300 μs for a final black hole of 10 solar masses), i.e., one can evolve through the very last moments of the inspiral when the two black holes merge, but even a single full orbit is not yet possible. Concretely, the computer code crashes when the space–time distortion becomes too severe. The recent computer simulations not only reflect an increase in raw computer power but also are due to theoretical work on how to construct good coordinates dynamically to deal with strong and even singular gravitational fields, and a new way to compute black hole initial data was developed. Work is in progress to obtain at least one orbit and to compute the gravitational waves generated in a black hole merger.

The evolution of the apparent horizon during a grazing black hole collision. Initially there are two separate horizons, which, during the merger, become enclosed by a third one. The coloring represents the curvature of the surface. The black holes appear to grow, because numerical grid points are falling toward and into the black hole.

In conclusion, we believe that black hole physics will be a very dynamic field in the coming years.

Acknowledgments

A.M.G. was supported by the National Science Foundation and the Packard Foundation. J.G. was partly supported by the German Bundesministerium für Bildung, Wissenschaft, Forschung und Technologie (BMBF/DLR) under contract 50 QQ 9602 3. The simulations in refs. 14 and 15 were performed at the Albert-Einstein-Institut and at National Center for Supercomputing Applications.

This paper is a summary of a session presented at the sixth annual German–American Frontiers of Science symposium, held June 8–10, 2000, at the Arnold and Mabel Beckman Center of the National Academies of Science and Engineering in Irvine, CA.

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• My Account Login
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Open access
• Published: 09 July 2021

Divergent reflections around the photon sphere of a black hole

• Albert Sneppen 1 , 2  

Scientific Reports volume  11 , Article number:  14247 ( 2021 ) Cite this article

31k Accesses

2 Citations

277 Altmetric

Metrics details

• Astronomy and astrophysics

An Author Correction to this article was published on 30 August 2021

This article has been updated

From any location outside the event horizon of a black hole there are an infinite number of trajectories for light to an observer. Each of these paths differ in the number of orbits revolved around the black hole and in their proximity to the last photon orbit. With simple numerical and a perturbed analytical solution to the null-geodesic equation of the Schwarzschild black hole we will reaffirm how each additional orbit is a factor \(e^{2 \pi }\) closer to the black hole’s optical edge. Consequently, the surface of the black hole and any background light will be mirrored infinitely in exponentially thinner slices around the last photon orbit. Furthermore, the introduced formalism proves how the entire trajectories of light in the strong field limit is prescribed by a diverging and a converging exponential. Lastly, the existence of the exponential family is generalized to the equatorial plane of the Kerr black hole with the exponentials dependence on spin derived. Thereby, proving that the distance between subsequent images increases and decreases for respectively retrograde and prograde images. In the limit of an extremely rotating Kerr black hole no logarithmic divergence exists for prograde trajectories.

Similar content being viewed by others

Characterization of the decametre sky at subarcminute resolution

Terawatt-scale attosecond X-ray pulses from a cascaded superradiant free-electron laser

Arbitrary engineering of spatial caustics with 3D-printed metasurfaces

Introduction.

Black holes are famously objects where the spatial paths of light are drastically bent by the curvature of space-time. While light itself cannot escape the central mass at the event horizon, at further distances light may orbit the black hole. In the generic case of a non-rotating and electrically neutral black hole [i.e. a Schwarzschild black hole 1 ] the event horizon is located at radial coordinate \(R_s=\frac{2GM}{c^2}\) , while photons may follow unstable circular orbits at \(\frac{3}{2} R_s\) , which is the so-called photon-sphere or last photon orbit. Any photon orbiting below this distance will plunge into the black hole, while light that remains further away will spiral out towards infinity.

However, depending on the photon’s proximity to the last photon orbit it may complete several orbits before spiralling into the event horizon or out towards infinity 2 , 3 . As we approach the limit where the photons graze the exact critical orbital radius the photon will orbit an infinite number of times. Inversely, from the perspective of an observer at infinity this implies that light from any point (from the event horizon to the background) may orbit the black hole an arbitrary number of times. For each of these paths the light will reach the observer slightly closer to the edge of the black hole’s shadow 4 . Therefore, the observer will see the entire surface of the event horizon and the entire universe repeating infinitely near the edges of the black hole. This infinite mapping has been extensively studied with the deflection angle diverging logarithmically in the strong field limit 2 , 4 , 5 , 6 , 7 , 8 .

However, we present a methodology, which differs from previous research by reformulating the trajectory of light in terms of a second order differential equation and quantifying its linear stability. In “ Simulated orbits ” we investigate how small deviations away from the optical edge of a black hole behave with a ray-tracing algorithm. We supplement with an analytical derivation in “ Linear stability ”. In both the numerical and analytical case we will show that small perturbations grow exponentially. Inversely, each additional orbit will be mapped to an exponentially thinner ring, with each subsequent image a factor \(e^{2 \pi }\) thinner. Ultimately, this paper investigates a well known problem from a new analytical perspective suggesting not only the deflection angle but the entire trajectories of light near the photon-sphere are prescribed by two duelling exponential functions.

Crucially, this approach is generalizable to any spherically symmetric black hole or even the equatorial plane of a spinning black hole. In “ Generalization to Kerr Metric ”, the exponentials dependence on the spin is derived and illustrated. Here it is proved for the first time that the spatial frequency of prograde and retrograde images will respectively increase and decrease from the Schwarzschild case.

Analytical setup

The Schwarzschild metric has the form in units with the speed of light, \(c=1\) :

Without loss of generality we can set the orbital plane of the light \(\theta =\frac{\pi }{2}\) . Introducing the two conserved quantities, angular momentum and energy, we can for a mass-less particle reduce the equation for the trajectory of light to 3 , 9 :

here b is the constant ratio of a photon’s angular momentum to energy. Rewriting the differential with \(\phi\) is only applicable if there is an angular evolution, so Eq. ( 2 ) does not apply in the limiting and trivial case of light moving radially towards or away from a black hole. Using the substitution \(u = R_s/r\) and differentiating both sides with \(\frac{d}{d\phi }\) yields the simple second order equation:

We can immediately reproduce the stationary orbit of the photon sphere for the Schwarzschild black hole by setting \(\frac{d^2u_{eq}}{d\phi ^2} = 0\) : \(r_{eq} = \frac{R_s}{u_{eq}} = \frac{3}{2} R_s\) . Note, the trivial equilibrium solution for \(u=0\) (i.e. at infinite distances from the black hole) will not be discussed further.

Simulated orbits

Given the differential equation (Eq. 3 ) relating distance to the angular deflection we can numerically integrate Eq. ( 3 ) using quartic Runga-Kutta (see Fig. 1 ). In this approach we are propagating the light from an observer to the black hole or the background universe. This yields the same light-path as the opposite direction, because the solutions of Eq. ( 2 ) are independent of the direction of the light. Integrating Eq. ( 3 ) requires two initial conditions: in Cartesian coordinates we center the black hole at the origin, set the initial direction of light to be \(\hat{v}_0 = (-1, 0)\) and the initial position \(\mathbf {r_0} = (d_0, b_0+\delta _0)\) . Here \(b_0\) (the critical impact parameter) is the distance within which photons are captured and outside which photons are deflected. Here \(d_0\) can be arbitrarily large given \(b_0\) at that distance which in the \(\lim _{d_0 \rightarrow \infty } b_0 = \frac{\sqrt{27}}{2} R_s\) becomes the photon capture radius commonly found in literature 10 . \(\delta _0\) is our initial perturbation which we use to avoid the ambiguity of defining the closest approach for light rays that spiral within the photon sphere. Importantly, \(\delta _0\) is interpretable as how far the observer is looking away from rim of the optical black hole.

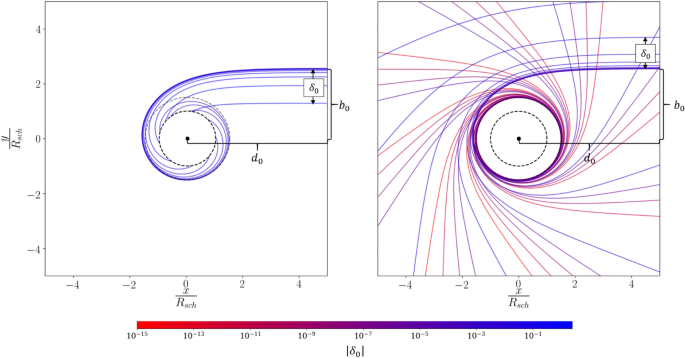
Simulated rays of light satisfying Eq. ( 3 ) with \(\delta _0 < 0\) (left) and \(\delta _0 > 0\) (right) with coloring indicating magnitude of \(\delta _0\) . The black hole is shaded in grey with the last photon orbit indicated with a dotted grey line. Each successive light-trajectory plotted is a factor of 2 closer to the photon capture radius with the resulting deflection angle increasing just below \(40^{\circ }\) . Thus, the logarithmic scaling towards the photon capture radius maps to a linear evolution in \(\phi\) .

The path for light with varying \(\delta _0\) can be seen in Fig. 1 . Positive and negative perturbations will respectively spiral out to infinity or plunge into the event horizon as expected. As \(\delta _0\) becomes smaller the deflection angle increases. Note, \(\phi\) increases linearly when moving logarithmically closer to the photon capture radius.

In Fig. 2 the results can be seen for positive (where the angle \(\phi\) is the unwrapped deflection angle) and negative perturbations (with the angle \(\phi\) being defined as the angle orbited around the black hole at the time when photons cross the event horizon). For large perturbations ( \(|\delta _0|>10^{-2}\) ) the relationship between angle and distance is not simply exponential. However in the small perturbation regime ( \(|\delta _0| < 10^{-2}\) ) a tight exponential relationship is visible. To determine the exponent in the exponential regime, we can fit, \(\phi = s \ln (\delta _0) + c\) , and with slope: \(s = -1.0000 \pm 0.0001\) . Inverting this expression for \(\delta _0\) implies that to achieve another orbit requires being a factor of \(f = e^{-2 \pi s} = 535.60 \pm 0.45\) closer to the optical edge of the black hole.

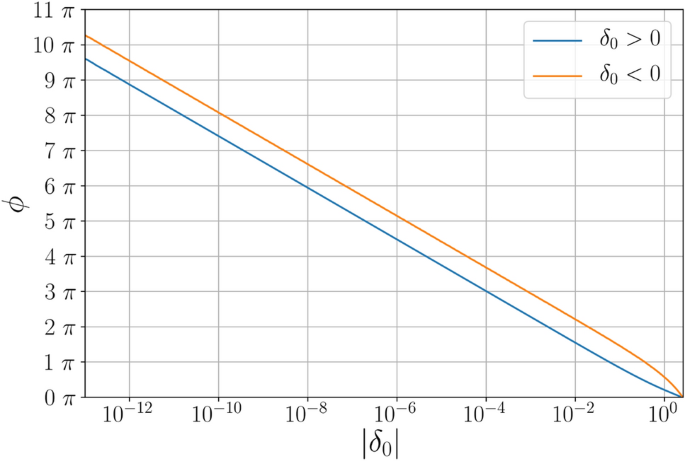
Angle of rotation for simulated light-rays as a function of deviations from the equilibrium (in dimensionless units with \(\delta _0 = l/R_s\) ) with \(\phi =0\) representing unbent light-rays. For both small positive and negative perturbations a clear exponential relation to \(\phi\) is visible.

Linear stability

To interpret these numerical results we will utilise linear stability analysis by adding small perturbations, \(u \rightarrow u_{eq} + \delta\) to the equilibrium solution of Eq. ( 3 ):

Linearlizing the equation around \(u_{eq} = \frac{2}{3}\) one gets:

which has the solution:

Evidently the first term grows in magnitude while the latter decreases, with the constants \(\delta _1\) and \(\delta _{-1}\) determining in which regime each term dominates. The constants are set by the initial conditions of the trajectory, which will be discussed further in “ Linear stability ”. Note the dual exponential form is to be expected as the equilibrium solution is a saddle point.

Intuition through manifolds

An alternate perspective on these exponential solutions is in the phase-space of Eq. ( 3 ). This is shown in Fig. 3 where for every initial condition ( \(u,\frac{du}{d\phi }\) ) a vector is plotted indicating the angular change in both variables (i.e. \(\frac{d u}{d \phi },\frac{d^2 u}{d \phi ^2}\) ). The trajectories terminating at \(u=1\) (i.e. \(r=R_s\) ) are the rays of light reaching the event horizon, while infinity is at \(u=0\) . Most trajectories will cross the photon-sphere with radial velocities, but if \(\frac{d u}{d \phi }=0\) on the photon-sphere then the photon will stay in its circular orbit indefinitely. Thus, orbits on the photon-sphere represent a fixed point in the phase-space.

Entire (left) and zoomed-in (right) phase-space portrait for light trajectories obeying Eq. ( 3 ) with the arrows’ coloring indicating the magnitude of change (brighter hues implies longer vectors). \(u = 1\) is the event-horizon, \(u=0\) represents infinity and \(u=\frac{2}{3}\) is at the photon sphere. If \(u=\frac{2}{3}\) and \(\frac{d u}{d \phi }=0\) the photons are on circular orbit, so this represents a fixed point. Notable, this is not a stable fixed point as deviations will in general grow. The stable and unstable manifolds are drawn which in the enlarged version are approximately linear. The stable manifold evidently represents a separatrix between the initial conditions of trajectories which will cross the event horizon or be ejected to infinity. Thus, the stable manifold is equivalent to the optical rim of the black hole.

The set of initial conditions which converge towards the photon sphere (which is called the stable manifold) is indicated with a blue line. Photons on this trajectory will asymptotically approach the photon sphere. Conversely, the unstable manifold (i.e. the set of initial conditions which reach the fixed point for \(\phi \rightarrow - \infty\) ) is plotted in red. The symmetry between stable and unstable manifolds seen in the phase-space is due to the Schwarzschild metric and therefore Eq. ( 14 ) being independent of the direction of time.

As seen in Fig. 3 (left) for the stable and unstable manifolds \(\frac{\partial u}{\partial \phi }\) is in general not linear in u , but when we are close to the fixed point ( \(\delta ^2 < |\delta |\) , see Eq. ( 5 )), the relationship becomes approximately linear. Importantly, there are two sets of eigenvectors around the photon sphere. The first with an eigenvalue of \(-1\) (the exponentially approaching term) and the unstable manifold with an eigenvalue of \(+1\) (the exponentially diverging term). Thus, the phase space clearly follows the intuition of Eq. ( 6 ).

The different signs of the eigenvalues proves that the fixed point is a saddle-point. A saddle-point is inherently unstable as a perturbation from the photon sphere will generically result in an exponential divergence. Evidently, the positive eigenvalue implies that a trajectory will diverge exponentially from the bound orbit with a factor \(e^{\pi n} = e^{\gamma n}\) for each half orbit n. Here the Lyapunov exponent, \(\gamma\) [following the definition by Johnson 11 ] characterizes the instability of the bound orbit relative to a half-orbit n. Thus, for the Schwarschild case for the photon sphere, \(\gamma =\pi\) .

Lastly, notice the eigenvalues around the fixed point in u are also the eigenvalues for r as \(\frac{\partial u}{\partial \phi } = u \Rightarrow \frac{\partial r}{\partial \phi } = -r\) . Therefore, the \(\pm 1\) eigenvalues in ( \(u,\frac{\partial u}{\partial \phi }\) ) corresponds to the eigenvalues \({\mp } 1\) in ( \(r,\frac{\partial r}{\partial \phi }\) ).

A tail of two exponentials

Given Eq. ( 6 ) we find the linearlized solutions:

When investigating the trajectory of light close to the black hole both exponential terms are needed to cross the equilibrium distance (see Eq. 7 ) or for \(\frac{d u}{d \phi }\) to change sign (as seen in Eq. 8 ). The importance of both exponential terms is also illustrated in Fig. 4 , where the light approaches the photon sphere exponentially (with each rotation bringing it a factor \(e^{2 \pi }\) closer) until at a crossover-angle of \(\phi _c \approx 6 \pi\) . After this the divergent \(e^{\phi }\) dominates and the light is ejected towards infinity. If \(\delta _{1}\) had the opposite sign then \(\frac{du}{d\phi }\) would remain negative so the crossover-angle would be on the last photon orbit, after which the light would diverge exponentially from the photon-sphere towards the black hole. Curiously, this implies the angle swept by the ray around the black hole prior to the photon sphere is similar to the angle swept by the ray from the photon-sphere to the event horizon.

Notably, the light-ray on the trajectory exactly on the rim of the black hole’s shadow (i.e. \(\delta _0=0\) ) is the solution which is exponentially approaching the photon-sphere indefinitely as it neither diverges towards the black hole or the background universe. It follow that the convergent exponential and in extension \(\delta _{-1}\) must be independent of \(\delta _{0}\) . Instead \(\delta _{-1}\) is set by the approximate distance where the linearised expression holds ( \(\delta _{-1} \approx 1\) ). Any deviations from the critical impact parameter, \(\delta _0 \ne 0\) , will grow exponentially, which implies \(\delta _1\) (the divergent exponential) is set by \(\delta _0\) . Thus, the order of magnitude estimates neatly follow the fitted lines in Fig. 4 .

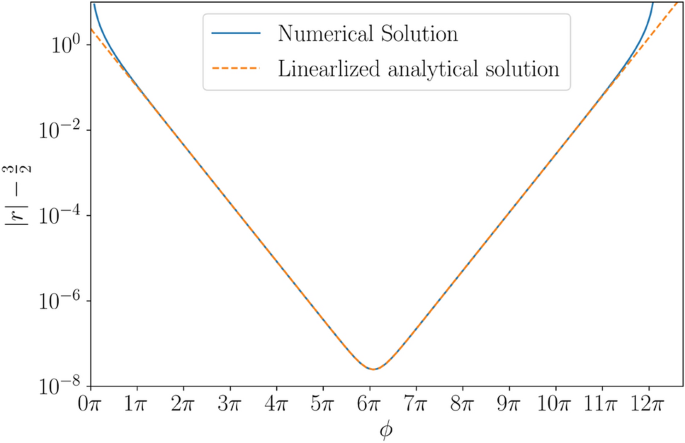
The radial distance between a light-ray (with \(\delta _0 = 10^{-15}\) ) and the last photon orbit as a function of deflection angle [in blue]. The predicted analytical combination of an exponentially declining ( \(e^{-\phi }\) ) and exponentially growing ( \(e^{\phi }\) ) term is indicated with a yellow dashed line. Evidently, each term dominates at different angles of \(\phi\) , with fitted lines suggesting \(\delta _1 \approx 10^{-16}\) and \(\delta _{-1} \approx 1\) . For \(u-u_{eq} \approx 1\) , the linearised solution no longer holds.

While the derivation is only applicable in the linearized regime the implications reach beyond the immediate surroundings of the photon-sphere, as the total deflection of light may be dominated by the angular rotation, while the photons are in the linearized regime. When investigating the total deflection angle or angle of rotation for light (as seen “ Simulated orbits ”) we are solving the trajectories for light moving away from \(u_{eq}\) , where the divergent exponential must dominate. Each additional orbit of light will be mapped a factor \(f = e^{2 \pi }\) nearer the rim of the black hole’s shadow, because decreasing \(\delta _0\) by a factor \(e^{2\pi }\) delays the exponentially growing term exactly one orbit. Furthermore, it should be noted that the predicted analytical value, \(f = e^{2 \pi } \approx 535.49\) , is remarkably close to the numerically fitted relationship seen in “ Simulated orbits ”.

Additionally, for deflected light it is noteworthy that the closest approach to the photon-sphere will only decrease by a factor of \(e^{\pi }\) for each additional orbit, because the cross-over angle is set by the intersection of the two exponential terms. Similarly, for light crossing the photon-sphere the angle swept from the event horizon to the photon-sphere is similar to the angle swept from the photon-sphere to the observer, as the cross-over angle is still defined by the intersection.

Generalization to Kerr Metric

It should be emphasised, that the Schwarzschild metric is the limiting case of a non-spinning black hole. Without this requirement one gets the so-called Kerr metric (Here written in Boyer-Lindquist coordinates with \(\Sigma =r^2+a^2 cos(\theta )\) and \(\Delta = r^2 - R_s r + a^2\) ):

here \(0 \le a \le 1\) is the angular momentum factor, so naturally the Kerr metric reduces to the Schwarzschild metric for \(a=0\) . For orbits in the equatorial plane (where a 2-dimensional analysis is still an exhaustive description) we set \(\theta =\frac{\pi }{2}\) . Further deliberation on non-equatorial orbits may be found through elliptic integrals 12 . Introducing the two conserved quantities, angular momentum and energy, the trajectory of photons reduces to 13 :

With b once more being the constant ratio of a photon’s angular momentum to energy. Differentiating both sides with \(\frac{d}{d\phi }\) yields a second order differential equation.

The phase portrait for Eq. ( 11 ) for \(a=0.5\) is illustrated in Fig. 5 . As before, the fixed point is set by the roots of \(\frac{dr^2}{d\phi ^2}\) , which will depend on a . In contrast to the Schwarzschild parameterization, Eq. ( 11 ) depends on b , so the critical impact parameter of prograde and retrograde orbits must be evaluated at any a 13 .

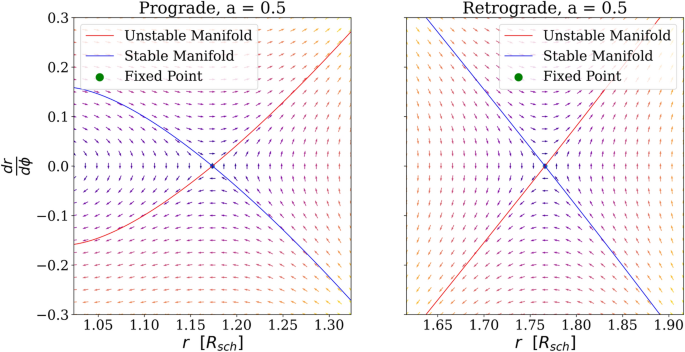
Phase-space portrait for light trajectories obeying Eq. ( 11 ) with \(a=0.5\) (left: prograde and right: retrograde) with the arrows’ coloring indicating the magnitude of change (brighter hues imply longer vectors). The stable and unstable manifolds are drawn which behave approximately linear with a flatter and steeper slope than Fig. 3 for respectively the prograde and retrograde orbits. Note the substitution \(u=\frac{1}{r}\) does not remove the critical impact parameter unlike the Schwarzschild case. Therefore the figure remains in r not u like Fig. 3 .

Retrograde and prograde orbits are obtained by evaluating the critical impact parameter with Eq. ( 12 ) and ( 13 ). For any given spin we may then determine the fixed points, \(r_{eq}\) such that \(\frac{\partial r^2}{\partial \phi ^2}=0\) . One root, \(\Delta =0\) , representing the event horizon with the remaining real root describing the photon circle (see Fig. 6 ). Linearizing generically yields:

Importantly, we once more we get a family of two exponentials and for the first time derive the exponential unwinding for the strong field limit of light:

For any spin, a , the exponential coefficient, s is shown in Fig. 6 . Evidently the fixed point is still a saddle point and therefore unstable. Here, the exponential divergent term corresponds to Lyapunov exponent of \(\gamma = \pi \sqrt{s}\) as trajectories will diverge from the photon sphere with a factor of \(e^{\pi \sqrt{s}}\) over a half orbit. Notable, the exponential coefficient s results in a even faster divergence of the logarithmic angle for retrograde orbits. For \(\lim _{a \rightarrow 1}(s_{retrograde})=\frac{27}{16}\) , so another orbit would require being a factor of \(f = e^{2 \pi \sqrt{27/16}} \approx 3500\) closer to the optical edge of the black hole. Conversely, for prograde orbits the exponential function unwinds evermore slowly for larger spins. For a black hole spinning with \(a=0.99\) (as potentially observed 15 ), where \(s=0.012\) , only a factor \(f = e^{2 \pi \sqrt{0.012}} \approx 2\) is required. Here, each repeated image would merely be a factor of 2 closer to the optical edge of the black hole. In the limit of an extreme Kerr field, \(\lim _{a \rightarrow 1}(s_{prograde}) = 0\) , the eigenvectors collapse and the fixed point becomes a degenerate node. Thus, an extremely rotating Kerr black hole has no exponential trajectories for the prograde motion.

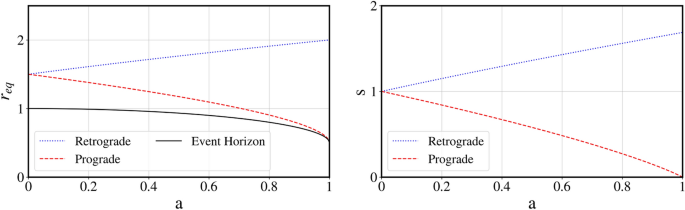
Radii of photon circle, \(r_{eq}\) (left), and linear coefficient of Taylor-expansion, s (right). Retrograde orbits (in dotted blue) and prograde orbits (in dashed red). The location of the photon circle is in agreement with 14 , while the generic result \(s>0\) for \(0 \le a < 1\) , implies that the fixed point will always be a saddle point with eigenvalues \(\pm \sqrt{s}\) and therefore unstable. Notable at \(a=1\) the two real fixed points of prograde motion bifurcate.

Thus, when viewing the equatorial plane of a spinning black hole both prograde and retrograde reflections display the exponential repetition, but prograde copies of a source will repeat rapidly compared to the retrograde copies. This asymmetry has potentially far-reaching applications to observables as any observational signature is limited by the brightness of subsequent images decreasing sharply 11 . Therefore, the rapid spatial repetition of prograde images will provide the first observational signatures of the exponential repetition within detection capabilities.

Lastly, the mathematical generality of two real eigenvalues existing for all a should not go unstated. Regardless of the spin of the black hole, there will always exist a family of a convergent and divergent exponential. These exponentials prescribe the entire trajectories of light near the photon orbits. Their prescription implies that any source object in the plane be repeated in an exponentially thinner series of copies, with the scale of repetitions set by the spin of the black hole.

This work introduces a family of two distinct exponential solutions which together provide a succinct description of the entire orbital trajectories of light near a Schwarzschild black hole. Thereby we provide analytical insight into the solutions previously developed 2 , 4 , 5 , 6 , 7 , 8 . Our formalism provides a few important interpretations. Firstly, it states that the deflection angle of background light will diverge logarithmically when the trajectory approaches the last photon orbit. Equivalently, from the perspective of a distant observer looking at the optical edge of the black hole (the photon capture radius) the entire background will be mapped to exponentially thinner rings. Secondly, the event horizon of the black hole itself will be mapped repeatedly in exponentially thinner rings just inside the photon capture radius. Therefore, any object accretting onto the black hole may be observed repeatedly nearer and nearer the optical edge. Thirdly, this edge of the black hole is the location of both the stable and unstable manifold.

The proof presented here is immediately generalizable to any spherically symmetric space-time (such as a Reissner–Nordstrøm black hole). Such metrics can similarly be written as a second order differential equation in r with steady state and perturbed solutions. Further work may investigate these exponentials, which will in general be characterised by a constant, \(s \ne 1\) , to be multiplied on \(\phi\) in the exponents of Eq. ( 14 ). Importantly, as seen in “ Generalization to Kerr Metric ”, our methodology may even be applied to non-spherically symmetric black holes, such as the spinning black holes of the Kerr Metric. With increasing spin, the exponential coefficient, s , of prograde trajectories decreases while retrograde conversely increase. Thus, proving that the side of the black hole which rotates towards the observer repeatedly mirrors the universe in wide bands. In the limit of an extremely rotating Kerr Hole, the \(s_{retrograde}=\frac{27}{16}\) and \(s_{prograde}=0\) . Thus, there is no logarithmic divergence for prograde reflections when \(a=1\) , but given any spin \(a<1\) , there exists an exponential family prescribing the trajectories.

Philosophically, there is a mathematical beauty within the dual exponentials of Eqs. ( 7 ) and ( 14 ). The exponentials prescribes, that an observer at infinity will see the entire black hole’s event horizon and anything accreting onto the black hole mapped infinitely when looking closer towards the photon capture radius of the black hole. Just beyond the photon capture radius, the exponentials dictate, that the observer will also see the entire universe mirrored in exponentially smaller slivers until the quantum limit. A divergence which certainly merits further reflection.

Change history

30 august 2021.

A Correction to this paper has been published: https://doi.org/10.1038/s41598-021-97272-w

Schwarzschild, K. On the gravitational field of a mass point according to Einstein’s theory. Abh. Konigl. Preuss. Akad. Wissenschaften Jahre 1906,92, Berlin,1907 1916 , 189–196 (1916).

Luminet, J. P. Image of a spherical black hole with thin accretion disk. Astron. Astrophys. 75 , 228–235 (1979).

ADS   Google Scholar  

Stuckey, W. M. The Schwarzschild black hole as a gravitational mirror. Am. J. Phys. 61 , 448–456. https://doi.org/10.1119/1.17434 (1993).

Article   ADS   Google Scholar  

Perlick, V. Gravitational lensing from a spacetime perspective. Preprint at https://arxiv.org/pdf/1010.3416.pdf (2010)

Darwin, C. The gravity field of a particle. Proc. Royal Soc. Lond. Ser. A 249 , 180–194. https://doi.org/10.1098/rspa.1959.0015 (1959) ( gr-qc/0208075 ).

Article   ADS   MathSciNet   MATH   Google Scholar  

Bozza, V. Gravitational lensing in the strong field limit. Phys. Rev. D 66 , 103001. https://doi.org/10.1103/PhysRevD.66.103001 (2002).

Article   ADS   CAS   Google Scholar  

Muñoz, G. Orbits of massless particles in the Schwarzschild metric: Exact solutions. Am. J. Phys. 82 , 564–573. https://doi.org/10.1119/1.4866274 (2014).

Gralla, S. E., Holz, D. E. & Wald, R. M. Black hole shadows, photon rings, and lensing rings. Phys. Rev. 100 , 024018. https://doi.org/10.1103/PhysRevD.100.024018 (2019) ( 1906.00873 ).

Musiri, S. Two conserved angular momenta in Schwarzschild spacetime geodesics. J. Phys. Conf. Series 1380 , 012168. https://doi.org/10.1088/1742-6596/1380/1/012168 (2019).

Article   Google Scholar  

Schutz, B. A First Course in General Relativity (Cambridge University Press, 2009).

Book   Google Scholar  

Johnson, M. D. et al. Universal interferometric signatures of a black hole’s photon ring. Sci. Adv. 6 , eaaz1310. https://doi.org/10.1126/sciadv.aaz1310 (2020) ( 1907.04329 ).

Article   ADS   PubMed   PubMed Central   Google Scholar  

Gralla, S. E. & Lupsasca, A. Lensing by Kerr black holes. Phys. Rev. D 101 , 044031. https://doi.org/10.1103/PhysRevD.101.044031 (2020) ( 1910.12873 ).

Article   ADS   MathSciNet   CAS   Google Scholar  

Cramer, C. R. Using the uncharged Kerr black hole as a gravitational mirror. Gen. Relativ. Gravit. 29 , 445–454. https://doi.org/10.1023/A:1018878515046 (1997) ( gr-qc/9510053 ).

Bardeen, J. M., Press, W. H. & Teukolsky, S. A. Rotating black holes: Locally nonrotating frames, energy extraction, and scalar synchrotron radiation. Astrophys. J. 178 , 347–370. https://doi.org/10.1086/151796 (1972).

McClintock, J. E. et al. The spin of the near-extreme Kerr black hole GRS 1915 + 105. Astrophys. J. 652 , 518–539. https://doi.org/10.1086/508457 (2006) ( astro-ph/0606076 ).

Download references

Acknowledgements

The author would like to thank Mogens Høgh Jensen, Martin Pessah, Charles Steinhardt and Nikki Arendse for useful deliberations and insightful feedback. The Cosmic Dawn Center (DAWN) is funded by the Danish National Research Foundation under Grant no. 140.

Author information

Authors and affiliations.

Niels Bohr Institute, University of Copenhagen, Blegdamsvej 17, Ø 2200, Copenhagen, Denmark

Albert Sneppen

Cosmic Dawn Center (DAWN), Copenhagen, Denmark

You can also search for this author in PubMed   Google Scholar

Contributions

A.S. wrote and reviewed the entire manuscript.

Corresponding author

Correspondence to Albert Sneppen .

Ethics declarations

Competing interests.

The authors declare no competing interests.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The original online version of this Article was revised: The original version of this Article contained an error in the spelling of the author Albert Sneppen which was incorrectly given as Albert Snepppen.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

Sneppen, A. Divergent reflections around the photon sphere of a black hole. Sci Rep 11 , 14247 (2021). https://doi.org/10.1038/s41598-021-93595-w

Download citation

Received : 12 May 2021

Accepted : 21 June 2021

Published : 09 July 2021

DOI : https://doi.org/10.1038/s41598-021-93595-w

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

By submitting a comment you agree to abide by our Terms and Community Guidelines . If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Help | Advanced Search

General Relativity and Quantum Cosmology

Title: gravitational lensing by spinning black holes in astrophysics, and in the movie interstellar.

Abstract: Interstellar is the first Hollywood movie to attempt depicting a black hole as it would actually be seen by somebody nearby. For this we developed a code called DNGR (Double Negative Gravitational Renderer) to solve the equations for ray-bundle (light-beam) propagation through the curved spacetime of a spinning (Kerr) black hole, and to render IMAX-quality, rapidly changing images. Our ray-bundle techniques were crucial for achieving IMAX-quality smoothness without flickering. This paper has four purposes: (i) To describe DNGR for physicists and CGI practitioners . (ii) To present the equations we use, when the camera is in arbitrary motion at an arbitrary location near a Kerr black hole, for mapping light sources to camera images via elliptical ray bundles. (iii) To describe new insights, from DNGR, into gravitational lensing when the camera is near the spinning black hole, rather than far away as in almost all prior studies. (iv) To describe how the images of the black hole Gargantua and its accretion disk, in the movie \emph{Interstellar}, were generated with DNGR. There are no new astrophysical insights in this accretion-disk section of the paper, but disk novices may find it pedagogically interesting, and movie buffs may find its discussions of Interstellar interesting.

Submission history

Access paper:.

• Other Formats

References & Citations

• INSPIRE HEP
• Google Scholar
• Semantic Scholar

1 blog link

Bibtex formatted citation.

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .