unit 12 trigonometry homework 13 double and half angle identities

7.1 Solving Trigonometric Equations with Identities

Learning objectives.

In this section, you will:

• Verify the fundamental trigonometric identities.
• Simplify trigonometric expressions using algebra and the identities.

In espionage movies, we see international spies with multiple passports, each claiming a different identity. However, we know that each of those passports represents the same person. The trigonometric identities act in a similar manner to multiple passports—there are many ways to represent the same trigonometric expression. Just as a spy will choose an Italian passport when traveling to Italy, we choose the identity that applies to the given scenario when solving a trigonometric equation.

In this section, we will begin an examination of the fundamental trigonometric identities, including how we can verify them and how we can use them to simplify trigonometric expressions.

Verifying the Fundamental Trigonometric Identities

Identities enable us to simplify complicated expressions. They are the basic tools of trigonometry used in solving trigonometric equations, just as factoring, finding common denominators, and using special formulas are the basic tools of solving algebraic equations. In fact, we use algebraic techniques constantly to simplify trigonometric expressions. Basic properties and formulas of algebra, such as the difference of squares formula and the perfect squares formula, will simplify the work involved with trigonometric expressions and equations. We already know that all of the trigonometric functions are related because they all are defined in terms of the unit circle. Consequently, any trigonometric identity can be written in many ways.

To verify the trigonometric identities, we usually start with the more complicated side of the equation and essentially rewrite the expression until it has been transformed into the same expression as the other side of the equation. Sometimes we have to factor expressions, expand expressions, find common denominators, or use other algebraic strategies to obtain the desired result. In this first section, we will work with the fundamental identities: the Pythagorean Identities , the even-odd identities, the reciprocal identities, and the quotient identities.

We will begin with the Pythagorean Identities (see Table 1 ), which are equations involving trigonometric functions based on the properties of a right triangle. We have already seen and used the first of these identifies, but now we will also use additional identities.

The second and third identities can be obtained by manipulating the first. The identity 1 + cot 2 θ = csc 2 θ 1 + cot 2 θ = csc 2 θ is found by rewriting the left side of the equation in terms of sine and cosine.

Prove: 1 + cot 2 θ = csc 2 θ 1 + cot 2 θ = csc 2 θ

Similarly, 1 + tan 2 θ = sec 2 θ 1 + tan 2 θ = sec 2 θ can be obtained by rewriting the left side of this identity in terms of sine and cosine. This gives

The next set of fundamental identities is the set of even-odd identities. The even-odd identities relate the value of a trigonometric function at a given angle to the value of the function at the opposite angle and determine whether the identity is odd or even. (See Table 2 ).

Recall that an odd function is one in which f (− x ) = − f ( x ) f (− x ) = − f ( x ) for all x x in the domain of f . f . The sine function is an odd function because sin ( − θ ) = − sin θ . sin ( − θ ) = − sin θ . The graph of an odd function is symmetric about the origin. For example, consider corresponding inputs of π 2 π 2 and − π 2 . − π 2 . The output of sin ( π 2 ) sin ( π 2 ) is opposite the output of sin ( − π 2 ) . sin ( − π 2 ) . Thus,

This is shown in Figure 2 .

Recall that an even function is one in which

The graph of an even function is symmetric about the y- axis. The cosine function is an even function because cos ( − θ ) = cos θ . cos ( − θ ) = cos θ . For example, consider corresponding inputs π 4 π 4 and − π 4 . − π 4 . The output of cos ( π 4 ) cos ( π 4 ) is the same as the output of cos ( − π 4 ) . cos ( − π 4 ) . Thus,

See Figure 3 .

For all θ θ in the domain of the sine and cosine functions, respectively, we can state the following:

• Since sin (− θ ) = − sin θ , sin (− θ ) = − sin θ , sine is an odd function.
• Since, cos (− θ ) = cos θ , cos (− θ ) = cos θ , cosine is an even function.

The other even-odd identities follow from the even and odd nature of the sine and cosine functions. For example, consider the tangent identity, tan (− θ ) = −tan θ . tan (− θ ) = −tan θ . We can interpret the tangent of a negative angle as tan (− θ ) = sin ( − θ ) cos (− θ ) = − sin θ cos θ = − tan θ . tan (− θ ) = sin ( − θ ) cos (− θ ) = − sin θ cos θ = − tan θ . Tangent is therefore an odd function, which means that tan ( − θ ) = − tan ( θ ) tan ( − θ ) = − tan ( θ ) for all θ θ in the domain of the tangent function .

The cotangent identity, cot ( − θ ) = − cot θ , cot ( − θ ) = − cot θ , also follows from the sine and cosine identities. We can interpret the cotangent of a negative angle as cot ( − θ ) = cos ( − θ ) sin ( − θ ) = cos θ − sin θ = − cot θ . cot ( − θ ) = cos ( − θ ) sin ( − θ ) = cos θ − sin θ = − cot θ . Cotangent is therefore an odd function, which means that cot ( − θ ) = − cot ( θ ) cot ( − θ ) = − cot ( θ ) for all θ θ in the domain of the cotangent function .

The cosecant function is the reciprocal of the sine function, which means that the cosecant of a negative angle will be interpreted as csc ( − θ ) = 1 sin ( − θ ) = 1 − sin θ = − csc θ . csc ( − θ ) = 1 sin ( − θ ) = 1 − sin θ = − csc θ . The cosecant function is therefore odd.

Finally, the secant function is the reciprocal of the cosine function, and the secant of a negative angle is interpreted as sec ( − θ ) = 1 cos ( − θ ) = 1 cos θ = sec θ . sec ( − θ ) = 1 cos ( − θ ) = 1 cos θ = sec θ . The secant function is therefore even.

To sum up, only two of the trigonometric functions, cosine and secant, are even. The other four functions are odd, verifying the even-odd identities.

The next set of fundamental identities is the set of reciprocal identities , which, as their name implies, relate trigonometric functions that are reciprocals of each other. See Table 3 .

The final set of identities is the set of quotient identities , which define relationships among certain trigonometric functions and can be very helpful in verifying other identities. See Table 4 .

The reciprocal and quotient identities are derived from the definitions of the basic trigonometric functions.

Summarizing Trigonometric Identities

The Pythagorean Identities are based on the properties of a right triangle.

The even-odd identities relate the value of a trigonometric function at a given angle to the value of the function at the opposite angle.

The reciprocal identities define reciprocals of the trigonometric functions.

The quotient identities define the relationship among the trigonometric functions.

Graphing the Equations of an Identity

Graph both sides of the identity cot θ = 1 tan θ . cot θ = 1 tan θ . In other words, on the graphing calculator, graph y = cot θ y = cot θ and y = 1 tan θ . y = 1 tan θ .

See Figure 4 .

We see only one graph because both expressions generate the same image. One is on top of the other. This is a good way to confirm an identity verified with analytical means. If both expressions give the same graph, then they are most likely identities.

Given a trigonometric identity, verify that it is true.

• Work on one side of the equation. It is usually better to start with the more complex side, as it is easier to simplify than to build.
• Look for opportunities to factor expressions, square a binomial, or add fractions.
• Noting which functions are in the final expression, look for opportunities to use the identities and make the proper substitutions.
• If these steps do not yield the desired result, try converting all terms to sines and cosines.

Verifying a Trigonometric Identity

Verify tan θ cos θ = sin θ . tan θ cos θ = sin θ .

We will start on the left side, as it is the more complicated side:

This identity was fairly simple to verify, as it only required writing tan θ tan θ in terms of sin θ sin θ and cos θ . cos θ .

Verify the identity csc θ cos θ tan θ = 1. csc θ cos θ tan θ = 1.

Verifying the Equivalency Using the Even-Odd Identities

Verify the following equivalency using the even-odd identities:

Working on the left side of the equation, we have

Verifying a Trigonometric Identity Involving sec 2 θ

Verify the identity sec 2 θ − 1 sec 2 θ = sin 2 θ sec 2 θ − 1 sec 2 θ = sin 2 θ

As the left side is more complicated, let’s begin there.

There is more than one way to verify an identity. Here is another possibility. Again, we can start with the left side.

In the first method, we used the identity sec 2 θ = tan 2 θ + 1 sec 2 θ = tan 2 θ + 1 and continued to simplify. In the second method, we split the fraction, putting both terms in the numerator over the common denominator. This problem illustrates that there are multiple ways we can verify an identity. Employing some creativity can sometimes simplify a procedure. As long as the substitutions are correct, the answer will be the same.

Show that cot θ csc θ = cos θ . cot θ csc θ = cos θ .

Creating and Verifying an Identity

Create an identity for the expression 2 tan θ sec θ 2 tan θ sec θ by rewriting strictly in terms of sine.

There are a number of ways to begin, but here we will use the quotient and reciprocal identities to rewrite the expression:

Verifying an Identity Using Algebra and Even/Odd Identities

Verify the identity:

Let’s start with the left side and simplify:

Verify the identity sin 2 θ − 1 tan θ sin θ − tan θ = sin θ + 1 tan θ . sin 2 θ − 1 tan θ sin θ − tan θ = sin θ + 1 tan θ .

Verifying an Identity Involving Cosines and Cotangents

Verify the identity: ( 1 − cos 2 x ) ( 1 + cot 2 x ) = 1. ( 1 − cos 2 x ) ( 1 + cot 2 x ) = 1.

We will work on the left side of the equation.

Using Algebra to Simplify Trigonometric Expressions

We have seen that algebra is very important in verifying trigonometric identities, but it is just as critical in simplifying trigonometric expressions before solving. Being familiar with the basic properties and formulas of algebra, such as the difference of squares formula, the perfect square formula, or substitution, will simplify the work involved with trigonometric expressions and equations.

For example, the equation ( sin x + 1 ) ( sin x − 1 ) = 0 ( sin x + 1 ) ( sin x − 1 ) = 0 resembles the equation ( x + 1 ) ( x − 1 ) = 0 , ( x + 1 ) ( x − 1 ) = 0 , which uses the factored form of the difference of squares. Using algebra makes finding a solution straightforward and familiar. We can set each factor equal to zero and solve. This is one example of recognizing algebraic patterns in trigonometric expressions or equations.

Another example is the difference of squares formula, a 2 − b 2 = ( a − b ) ( a + b ) , a 2 − b 2 = ( a − b ) ( a + b ) , which is widely used in many areas other than mathematics, such as engineering, architecture, and physics. We can also create our own identities by continually expanding an expression and making the appropriate substitutions. Using algebraic properties and formulas makes many trigonometric equations easier to understand and solve.

Writing the Trigonometric Expression as an Algebraic Expression

Write the following trigonometric expression as an algebraic expression: 2 cos 2 θ + cos θ − 1. 2 cos 2 θ + cos θ − 1.

Notice that the pattern displayed has the same form as a standard quadratic expression, a x 2 + b x + c . a x 2 + b x + c . Letting cos θ = x , cos θ = x , we can rewrite the expression as follows:

This expression can be factored as ( 2 x − 1 ) ( x + 1 ) . ( 2 x − 1 ) ( x + 1 ) . If it were set equal to zero and we wanted to solve the equation, we would use the zero factor property and solve each factor for x . x . At this point, we would replace x x with cos θ cos θ and solve for θ . θ .

Rewriting a Trigonometric Expression Using the Difference of Squares

Rewrite the trigonometric expression: 4 cos 2 θ − 1. 4 cos 2 θ − 1.

Notice that both the coefficient and the trigonometric expression in the first term are squared, and the square of the number 1 is 1. This is the difference of squares. Thus,

If this expression were written in the form of an equation set equal to zero, we could solve each factor using the zero factor property. We could also use substitution like we did in the previous problem and let cos θ = x , cos θ = x , rewrite the expression as 4 x 2 − 1 , 4 x 2 − 1 , and factor ( 2 x − 1 ) ( 2 x + 1 ) . ( 2 x − 1 ) ( 2 x + 1 ) . Then replace x x with cos θ cos θ and solve for the angle.

Rewrite the trigonometric expression: 25 − 9 sin 2 θ . 25 − 9 sin 2 θ .

Simplify by Rewriting and Using Substitution

Simplify the expression by rewriting and using identities:

We can start with the Pythagorean identity.

Now we can simplify by substituting 1 + cot 2 θ 1 + cot 2 θ for csc 2 θ . csc 2 θ . We have

Use algebraic techniques to verify the identity: cos θ 1 + sin θ = 1 − sin θ cos θ . cos θ 1 + sin θ = 1 − sin θ cos θ .

(Hint: Multiply the numerator and denominator on the left side by 1 − sin θ . ) 1 − sin θ . )

Access these online resources for additional instruction and practice with the fundamental trigonometric identities.

• Fundamental Trigonometric Identities
• Verifying Trigonometric Identities

7.1 Section Exercises

We know g ( x ) = cos x g ( x ) = cos x is an even function, and f ( x ) = sin x f ( x ) = sin x and h ( x ) = tan x h ( x ) = tan x are odd functions. What about G ( x ) = cos 2 x , F ( x ) = sin 2 x , G ( x ) = cos 2 x , F ( x ) = sin 2 x , and H ( x ) = tan 2 x ? H ( x ) = tan 2 x ? Are they even, odd, or neither? Why?

Examine the graph of f ( x ) = sec x f ( x ) = sec x on the interval [ − π , π ] . [ − π , π ] . How can we tell whether the function is even or odd by only observing the graph of f ( x ) = sec x ? f ( x ) = sec x ?

After examining the reciprocal identity for sec t , sec t , explain why the function is undefined at certain points.

All of the Pythagorean Identities are related. Describe how to manipulate the equations to get from sin 2 t + cos 2 t = 1 sin 2 t + cos 2 t = 1 to the other forms.

For the following exercises, use the fundamental identities to fully simplify the expression.

sin x cos x sec x sin x cos x sec x

sin ( − x ) cos ( − x ) csc ( − x ) sin ( − x ) cos ( − x ) csc ( − x )

tan x sin x + sec x cos 2 x tan x sin x + sec x cos 2 x

csc x + cos x cot ( − x ) csc x + cos x cot ( − x )

cot t + tan t sec ( − t ) cot t + tan t sec ( − t )

3 sin 3 t csc t + cos 2 t + 2 cos ( − t ) cos t 3 sin 3 t csc t + cos 2 t + 2 cos ( − t ) cos t

− tan ( − x ) cot ( − x ) − tan ( − x ) cot ( − x )

− sin ( − x ) cos x sec x csc x tan x cot x − sin ( − x ) cos x sec x csc x tan x cot x

1 + tan 2 θ csc 2 θ + sin 2 θ + 1 sec 2 θ 1 + tan 2 θ csc 2 θ + sin 2 θ + 1 sec 2 θ

( tan x csc 2 x + tan x sec 2 x ) ( 1 + tan x 1 + cot x ) − 1 cos 2 x ( tan x csc 2 x + tan x sec 2 x ) ( 1 + tan x 1 + cot x ) − 1 cos 2 x

1 − cos 2 x tan 2 x + 2 sin 2 x 1 − cos 2 x tan 2 x + 2 sin 2 x

For the following exercises, simplify the first trigonometric expression by writing the simplified form in terms of the second expression.

tan x + cot x csc x ; cos x tan x + cot x csc x ; cos x

sec x + csc x 1 + tan x ; sin x sec x + csc x 1 + tan x ; sin x

cos x 1 + sin x + tan x ; cos x cos x 1 + sin x + tan x ; cos x

1 sin x cos x − cot x ; cot x 1 sin x cos x − cot x ; cot x

1 1 − cos x − cos x 1 + cos x ; csc x 1 1 − cos x − cos x 1 + cos x ; csc x

( sec x + csc x ) ( sin x + cos x ) − 2 − cot x ; tan x ( sec x + csc x ) ( sin x + cos x ) − 2 − cot x ; tan x

1 csc x − sin x ; sec x  and  tan x 1 csc x − sin x ; sec x  and  tan x

1 − sin x 1 + sin x − 1 + sin x 1 − sin x ; sec x  and  tan x 1 − sin x 1 + sin x − 1 + sin x 1 − sin x ; sec x  and  tan x

tan x ; sec x tan x ; sec x

sec x ; cot x sec x ; cot x

sec x ; sin x sec x ; sin x

cot x ; sin x cot x ; sin x

cot x ; csc x cot x ; csc x

For the following exercises, verify the identity.

cos x − cos 3 x = cos x sin 2 x cos x − cos 3 x = cos x sin 2 x

cos x ( tan x − sec ( − x ) ) = sin x − 1 cos x ( tan x − sec ( − x ) ) = sin x − 1

1 + sin 2 x cos 2 x = 1 cos 2 x + sin 2 x cos 2 x = 1 + 2 tan 2 x 1 + sin 2 x cos 2 x = 1 cos 2 x + sin 2 x cos 2 x = 1 + 2 tan 2 x

( sin x + cos x ) 2 = 1 + 2 sin x cos x ( sin x + cos x ) 2 = 1 + 2 sin x cos x

cos 2 x − tan 2 x = 2 − sin 2 x − sec 2 x cos 2 x − tan 2 x = 2 − sin 2 x − sec 2 x

For the following exercises, prove or disprove the identity.

1 1 + cos x − 1 1 − cos ( − x ) = − 2 cot x csc x 1 1 + cos x − 1 1 − cos ( − x ) = − 2 cot x csc x

csc 2 x ( 1 + sin 2 x ) = cot 2 x csc 2 x ( 1 + sin 2 x ) = cot 2 x

( sec 2 ( − x ) − tan 2 x tan x ) ( 2 + 2 tan x 2 + 2 cot x ) − 2 sin 2 x = cos 2 x ( sec 2 ( − x ) − tan 2 x tan x ) ( 2 + 2 tan x 2 + 2 cot x ) − 2 sin 2 x = cos 2 x

tan x sec x sin ( − x ) = cos 2 x tan x sec x sin ( − x ) = cos 2 x

sec ( − x ) tan x + cot x = − sin ( − x ) sec ( − x ) tan x + cot x = − sin ( − x )

1 + sin x cos x = cos x 1 + sin ( − x ) 1 + sin x cos x = cos x 1 + sin ( − x )

For the following exercises, determine whether the identity is true or false. If false, find an appropriate equivalent expression.

cos 2 θ − sin 2 θ 1 − tan 2 θ = sin 2 θ cos 2 θ − sin 2 θ 1 − tan 2 θ = sin 2 θ

3 sin 2 θ + 4 cos 2 θ = 3 + cos 2 θ 3 sin 2 θ + 4 cos 2 θ = 3 + cos 2 θ

sec θ + tan θ cot θ + cos θ = sec 2 θ sec θ + tan θ cot θ + cos θ = sec 2 θ

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/precalculus-2e/pages/1-introduction-to-functions

• Authors: Jay Abramson
• Publisher/website: OpenStax
• Book title: Precalculus 2e
• Publication date: Dec 21, 2021
• Location: Houston, Texas
• Book URL: https://openstax.org/books/precalculus-2e/pages/1-introduction-to-functions
• Section URL: https://openstax.org/books/precalculus-2e/pages/7-1-solving-trigonometric-equations-with-identities

© Jan 9, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Chapter 5: Equations and Identities

Exercises: 5.3 Trigonometric Identities

                              skills.

Practice each skill in the Homework Problems listed:

• Recognize identities
• Verify identities
• Rewrite expressions using identities
• Use identities to evaluate expressions
• Solve trigonometric equations
• Given one trig ratio, find the others

Suggested Problems

Exercises Homework 5.3

Exercise group.

For Problems 1–8, decide which of the following equations are identities. Explain your reasoning.

[latex]\left(\sqrt{a} + \sqrt{b}\right)^2 = a + b[/latex]

[latex]\sqrt{a^2 - b^2} = a - b[/latex]

[latex]\dfrac{1}{a + b} = \dfrac{1}{a} + \dfrac{1}{b}[/latex]

[latex]\dfrac{a + b}{a} = b[/latex]

[latex]\tan (\alpha + \beta) = \dfrac{\sin (\alpha + \beta)}{\cos (\alpha + \beta)}[/latex]

[latex]\dfrac{1}{\tan \theta} = \dfrac{\cos \theta}{\sin \theta}[/latex]

[latex](1 + \tan \theta)^2 = 1 + \tan^2 \theta[/latex]

[latex]\sqrt{1 - \sin^2 \phi} = 1 - \sin \phi[/latex]

For Problems 9–16, use graphs to decide which of the following equations are identities.

[latex]\sin 2t = 2 \sin t[/latex]

[latex]\cos \theta + \sin \theta = 1[/latex]

[latex]\sin (30° + \beta) = \dfrac{1}{2} + \sin \beta[/latex]

[latex]\cos (90° - C) = \sin C[/latex]

[latex]\tan (90° - \theta) = \dfrac{1}{\tan \theta}[/latex]

[latex]\tan 2\theta = \dfrac{2\tan \theta}{1 - \tan^2 \theta}[/latex]

[latex]\dfrac{\tan^2 x}{1 + \tan^2 x} = \sin^2 x[/latex]

[latex]\tan x + \dfrac{1}{\tan x} = \sin x \cos x[/latex]

For Problems 17–26, show that the equation is an identity by transforming the left side into the right side.

[latex](1 + \sin w)(1 - \sin w) = \cos^2 w[/latex]

[latex](\cos \theta - 1)(\cos \theta + 1) = -\sin^2 \theta[/latex]

[latex](\cos \theta - \sin \theta)^2 = 1 - 2 \sin \theta \cos \theta[/latex]

[latex]\sin^2 x - \cos^2 x = 1 - 2\cos^2 x[/latex]

[latex]\tan \theta \cos \theta = \sin \theta[/latex]

[latex]\dfrac{\sin \mu}{\tan \mu} = \cos \mu[/latex]

[latex]\cos^4 x - \sin^4 x = \cos^2 x - \sin^2 x[/latex]

[latex]1 - 2\cos^2 v + \cos^4 v = \sin^4 v[/latex]

[latex]\dfrac{\sin u}{1 + \cos u} = \dfrac{1 - \cos u}{\sin u}[/latex]

Multiply numerator and denominator of the left side by [latex]1 - \cos u{.}[/latex]

[latex]\dfrac{\sin v}{1 - \cos v} = \dfrac{\tan v(1 + \sin v)}{\cos v}[/latex]

Multiply numerator and denominator of the left side by [latex]1 + \sin v{.}[/latex]

For Problems 27–34, simplify, using identities as necessary.

[latex]\dfrac{1}{\cos^2 \beta}- \dfrac{\sin^2 \beta}{\cos^2 \beta}[/latex]

[latex]\dfrac{1}{\sin^2 \phi}- \dfrac{1}{\tan^2 \phi}[/latex]

[latex]\cos^2 \alpha (1 + \tan^2 \alpha)[/latex]

[latex]\cos^3 \phi + \sin^2 \phi \cos \phi[/latex]

[latex]\tan^2 A - \tan^2 A \sin^2 A[/latex]

[latex]\cos^2 B \tan^2 B + \cos^2 B[/latex]

[latex]\dfrac{1 - \cos^2 z}{\cos^2 z}[/latex]

[latex]\dfrac{\sin t}{\cos t \tan t}[/latex]

For Problems 35–40, evaluate without using a calculator.

[latex]3\cos^2 1.7° + 3\sin^2 1.7°[/latex]

[latex]4 - \cos^2 338° - \sin^2 338°[/latex]

[latex](\cos^2 20° + \sin^2 20°)^4[/latex]

[latex]\dfrac{18}{\cos^2 17° + \sin^2 17°}[/latex]

[latex]\dfrac{6}{\cos^2 53°} - 6 \tan^2 53°[/latex]

[latex]\dfrac{1}{\sin^2 102°} - \dfrac{\cos^2 102°}{\sin^2 102°}[/latex]

For Problems 41–46, one side of an identity is given. Graph the expression and make a conjecture about the other side of the identity.

[latex]2\cos^2 \theta - 1 = ?[/latex]

[latex]1 - 2\sin^2 \left(\dfrac{\theta}{2}\right) = ?[/latex]

[latex]1 - \dfrac{\sin^2 x}{1 + \cos x} = ?[/latex]

[latex]\dfrac{\sin x}{\sqrt{1 - \sin^2 x}} = ?[/latex]

[latex]2\tan t \cos^2 t = ?[/latex]

[latex]\dfrac{2 \tan t}{1 - \tan^2 t} = ?[/latex]

For Problems 47–50, use identities to rewrite each expression.

[latex]2 - \cos^2 \theta + 2 \sin \theta~~~[/latex] as an expression in [latex]\sin \theta[/latex] only

[latex]3\sin^2 B + 2\cos B - 4~~~[/latex] as an expression in [latex]\cos B[/latex] only

[latex]\cos^2 \phi - 2\sin^2 \phi~~~[/latex] as an expression in [latex]\cos \phi[/latex] only

[latex]\cos^2 \phi \sin^2 \phi~~~[/latex] as an expression in [latex]\sin \phi[/latex] only

For Problems 51–58, solve the equation for [latex]0° \le\theta\le 360°{.}[/latex] Round angles to three decimal places if necessary.

[latex]\cos \theta - \sin^2 \theta + 1 = 0[/latex]

[latex]4\sin \theta + 2\cos^2 \theta - 3 = -1[/latex]

[latex]1 - \sin \theta - 2\cos^2 \theta = 0[/latex]

[latex]3\cos^2 \theta - \sin^2 \theta = 2[/latex]

[latex]2\cos \theta \tan \theta + 1 = 0[/latex]

[latex]\cos \theta - \sin \theta = 0[/latex]

[latex]\dfrac{1}{3}\cos \theta = \sin \theta[/latex]

[latex]5\sin C = 2\cos C[/latex]

For Problems 59–62, use identities to find exact values for the other two trig ratios.

[latex]\cos A = \dfrac{12}{13}~~~[/latex] and [latex]~270° \lt\ A \lt 360°[/latex]

[latex]\sin B = \dfrac{-3}{5}~~~[/latex] and [latex]~180° \lt\ B \lt 270°[/latex]

[latex]\sin \phi = \dfrac{1}{7}~~~[/latex] and [latex]~90° \lt\ \phi \lt 180°[/latex]

[latex]\cos t = \dfrac{-2}{3}~~~[/latex] and [latex]~180° \lt\ t \lt 270°[/latex]

For Problems 63–66, use the identity below to find the sine and cosine of the angle. [latex]{1 + \tan^2 \theta = \dfrac{1}{\cos^2 \theta}}[/latex]

[latex]\tan \theta = -\dfrac{1}{2}~~~[/latex] and [latex]~270° \lt\ \theta \lt 360°[/latex]

[latex]\tan \theta = 2~~~[/latex] and [latex]~180° \lt\ \theta \lt 270°[/latex]

[latex]\tan \theta = \dfrac{3}{4}~~~[/latex] and [latex]~180° \lt\ \theta \lt 270°[/latex]

[latex]\tan \theta = -3~~~[/latex] and [latex]~90° \lt\ \theta \lt 180°[/latex]

For Problems 67–72, find exact values for the sine, cosine, and tangent of the angle.

[latex]2\cos A + 9 = 8~~~[/latex] and [latex]~90° \lt\ A \lt 180°[/latex]

[latex]25\sin B + 8 = -12~~~[/latex] and [latex]~180° \lt\ B \lt 270°[/latex]

[latex]8\tan \beta + 5 = -11~~~[/latex] and [latex]~90° \lt\ \beta \lt 180°[/latex]

[latex]6(\tan \beta - 4) = -24~~~[/latex] and [latex]~90° \lt\ \beta \lt 270°[/latex]

[latex]\tan^2 C - \dfrac{1}{4} = 0~~~[/latex] and [latex]~0° \lt\ C \lt 180°[/latex]

[latex]4\cos^2 A - \cos A = 0~~~[/latex] and [latex]~00° \lt\ A \lt 180°[/latex]

For Problems 73–76, prove the identity by rewriting tangents in terms of sines and cosines. (These problems involve simplifying complex fractions. See the Algebra Refresher to review this skill.)

[latex]\dfrac{\tan \alpha}{1 + \tan \alpha} = \dfrac{\sin \alpha}{\sin \alpha + \cos \alpha}[/latex]

[latex]\dfrac{1 - \tan u}{1 + \tan u} = \dfrac{\cos u - \sin u}{\cos u + \sin u}[/latex]

[latex]\dfrac{1 + \tan^2 \beta}{1 - \tan^2 \beta} = \dfrac{1}{\cos^2 \beta - \sin^2 \beta}[/latex]

[latex]\tan^2 v - \sin^2 v = \tan^2 v \sin^2 v[/latex]

Prove the Pythagorean identity [latex]\cos^2 \theta + \sin^2 \theta = 1[/latex] by carrying out the following steps. Sketch an angle [latex]\theta[/latex] in standard position and label a point [latex](x,y)[/latex] on the terminal side, at a distance [latex]r[/latex] from the vertex.

• Begin with the equation [latex]\sqrt{x^2 + y^2} = r{,}[/latex] and square both sides.
• Divide both sides of your equation from part (a) by [latex]r^2{.}[/latex]
• Write the left side of the equation as the sum of the squares of two fractions.
• Substitute the appropriate trigonometric ratio for each fraction.

Prove the tangent identity [latex]\tan \theta = \dfrac{\sin \theta}{\cos \theta}[/latex] by carrying out the following steps. Sketch an angle [latex]\theta[/latex] in standard position and label a point [latex](x,y)[/latex] on the terminal side, at a distance [latex]r[/latex] from the vertex.

• Write [latex]\sin \theta[/latex] in terms of [latex]y[/latex] and [latex]r{,}[/latex] and solve for [latex]y{.}[/latex]
• Write [latex]\cos \theta[/latex] in terms of [latex]x[/latex] and [latex]r{,}[/latex] and solve for [latex]x{.}[/latex]
• Write [latex]\tan \theta[/latex] in terms of [latex]x[/latex] and [latex]y{,}[/latex] then substitute your results from parts (a) and (b).
• Simplify your fraction in part (c).

Trigonometry Copyright © 2024 by Bimal Kunwor; Donna Densmore; Jared Eusea; and Yi Zhen. All Rights Reserved.

Study Guides > Precalculus II

Double angle, half angle, and reduction formulas, using double-angle formulas to find exact values, a general note: double-angle formulas, how to: given the tangent of an angle and the quadrant in which it is located, use the double-angle formulas to find the exact value..

• Draw a triangle to reflect the given information.
• Determine the correct double-angle formula.
• Substitute values into the formula based on the triangle.

Example 1: Using a Double-Angle Formula to Find the Exact Value Involving Tangent

• [latex]\sin \left(2\theta \right)[/latex]
• [latex]\cos \left(2\theta \right)[/latex]
• [latex]\tan \left(2\theta \right)[/latex]

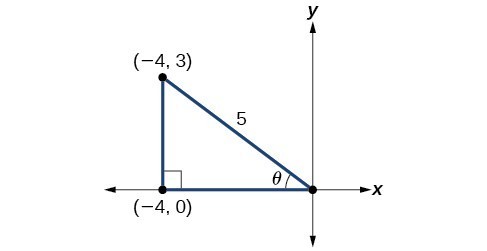
• Let’s begin by writing the double-angle formula for sine. [latex]\sin \left(2\theta \right)=2\sin \theta \cos \theta [/latex] We see that we to need to find [latex]\sin \theta [/latex] and [latex]\cos \theta [/latex]. Based on Figure 2, we see that the hypotenuse equals 5, so [latex]\sin \theta =\frac{3}{5}[/latex], and [latex]\cos \theta =−\frac{4}{5}[/latex]. Substitute these values into the equation, and simplify. Thus, [latex]\begin{array}{l}\sin \left(2\theta \right)=2\left(\frac{3}{5}\right)\left(−\frac{4}{5}\right)\hfill \\ \text{ }=−\frac{24}{25}\hfill \end{array}[/latex]
• Write the double-angle formula for cosine. [latex]\cos \left(2\theta \right)={\cos }^{2}\theta -{\sin }^{2}\theta [/latex] Again, substitute the values of the sine and cosine into the equation, and simplify. [latex]\begin{array}{l}\cos \left(2\theta \right)={\left(−\frac{4}{5}\right)}^{2}−{\left(\frac{3}{5}\right)}^{2}\hfill \\ \text{ }=\frac{16}{25}−\frac{9}{25}\hfill \\ \text{ }=\frac{7}{25}\hfill \end{array}[/latex]
• Write the double-angle formula for tangent. [latex]\tan \left(2\theta \right)=\frac{2\tan \theta }{1−{\tan }^{2}\theta }[/latex] In this formula, we need the tangent, which we were given as [latex]\tan \theta =−\frac{3}{4}[/latex]. Substitute this value into the equation, and simplify. [latex]\begin{array}{l}\tan \left(2\theta \right)=\frac{2\left(-\frac{3}{4}\right)}{1-{\left(-\frac{3}{4}\right)}^{2}}\hfill \\ \text{ }=\frac{-\frac{3}{2}}{1-\frac{9}{16}}\hfill \\ \text{ }=-\frac{3}{2}\left(\frac{16}{7}\right)\hfill \\ \text{ }=-\frac{24}{7}\hfill \end{array}[/latex]

Example 2: Using the Double-Angle Formula for Cosine without Exact Values

[latex]\begin{array}{l}\cos \left(6x\right)=\cos \left(3x+3x\right)\hfill \\ \text{ }=\cos 3x\cos 3x-\sin 3x\sin 3x\hfill \\ \text{ }={\cos }^{2}3x-{\sin }^{2}3x\hfill \end{array}[/latex]

Analysis of the Solution

Using double-angle formulas to verify identities, example 3: using the double-angle formulas to establish an identity, example 4: verifying a double-angle identity for tangent, use reduction formulas to simplify an expression, a general note: reduction formulas, example 5: writing an equivalent expression not containing powers greater than 1, example 6: using the power-reducing formulas to prove an identity, using half-angle formulas to find exact values, a general note: half-angle formulas, example 7: using a half-angle formula to find the exact value of a sine function, how to: given the tangent of an angle and the quadrant in which the angle lies, find the exact values of trigonometric functions of half of the angle..

• Draw a triangle to represent the given information.
• Determine the correct half-angle formula.

Example 8: Finding Exact Values Using Half-Angle Identities

• [latex]\sin \left(\frac{\alpha }{2}\right)[/latex]
• [latex]\cos \left(\frac{\alpha }{2}\right)[/latex]
• [latex]\tan \left(\frac{\alpha }{2}\right)[/latex]

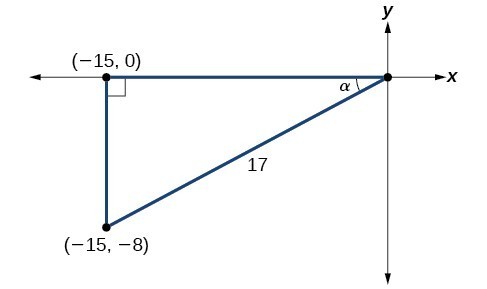
• Before we start, we must remember that, if [latex]\alpha [/latex] is in quadrant III, then [latex]180^\circ <\alpha <270^\circ [/latex], so [latex]\frac{180^\circ }{2}<\frac{\alpha }{2}<\frac{270^\circ }{2}[/latex]. This means that the terminal side of [latex]\frac{\alpha }{2}[/latex] is in quadrant II, since [latex]90^\circ <\frac{\alpha }{2}<135^\circ [/latex].To find [latex]\sin \frac{\alpha }{2}[/latex], we begin by writing the half-angle formula for sine. Then we substitute the value of the cosine we found from the triangle in Figure 3 and simplify. [latex]\begin{array}{l}\begin{array}{l}\\ \sin \frac{\alpha }{2}=\pm \sqrt{\frac{1-\cos \alpha }{2}}\end{array}\hfill \\ \text{ }=\pm \sqrt{\frac{1-\left(-\frac{15}{17}\right)}{2}}\hfill \\ \text{ }=\pm \sqrt{\frac{\frac{32}{17}}{2}}\hfill \\ \text{ }=\pm \sqrt{\frac{32}{17}\cdot \frac{1}{2}}\hfill \\ \text{ }=\pm \sqrt{\frac{16}{17}}\hfill \\ \text{ }=\pm \frac{4}{\sqrt{17}}\hfill \\ \text{ }=\frac{4\sqrt{17}}{17}\hfill \end{array}[/latex] We choose the positive value of [latex]\sin \frac{\alpha }{2}[/latex] because the angle terminates in quadrant II and sine is positive in quadrant II.
• To find [latex]\cos \frac{\alpha }{2}[/latex], we will write the half-angle formula for cosine, substitute the value of the cosine we found from the triangle in Figure 3, and simplify. [latex]\begin{array}{l}\begin{array}{l}\hfill \\ \hfill \\ \cos \frac{\alpha }{2}=\pm \sqrt{\frac{1+\cos \alpha }{2}}\hfill \end{array}\hfill \\ \text{ }=\pm \sqrt{\frac{1+\left(-\frac{15}{17}\right)}{2}}\hfill \\ \text{ }=\pm \sqrt{\frac{\frac{2}{17}}{2}}\hfill \\ \text{ }=\pm \sqrt{\frac{2}{17}\cdot \frac{1}{2}}\hfill \\ \text{ }=\pm \sqrt{\frac{1}{17}}\hfill \\ \text{ }=-\frac{\sqrt{17}}{17}\hfill \end{array}[/latex] We choose the negative value of [latex]\cos \frac{\alpha }{2}[/latex] because the angle is in quadrant II because cosine is negative in quadrant II.
• To find [latex]\tan \frac{\alpha }{2}[/latex], we write the half-angle formula for tangent. Again, we substitute the value of the cosine we found from the triangle in Figure 3 and simplify. [latex]\begin{array}{l}\begin{array}{l}\hfill \\ \tan \frac{\alpha }{2}=\pm \sqrt{\frac{1-\cos \alpha }{1+\cos \alpha }}\hfill \end{array}\hfill \\ \text{ }=\pm \sqrt{\frac{1-\left(-\frac{15}{17}\right)}{1+\left(-\frac{15}{17}\right)}}\hfill \\ \text{ }=\pm \sqrt{\frac{\frac{32}{17}}{\frac{2}{17}}}\hfill \\ \text{ }=\pm \sqrt{\frac{32}{2}}\hfill \\ \text{ }=-\sqrt{16}\hfill \\ \text{ }=-4\hfill \end{array}[/latex] We choose the negative value of [latex]\tan \frac{\alpha }{2}[/latex] because [latex]\frac{\alpha }{2}[/latex] lies in quadrant II, and tangent is negative in quadrant II.

Example 9: Finding the Measurement of a Half Angle

Key Equations

Key concepts.

• Double-angle identities are derived from the sum formulas of the fundamental trigonometric functions: sine, cosine, and tangent.
• Reduction formulas are especially useful in calculus, as they allow us to reduce the power of the trigonometric term.
• Half-angle formulas allow us to find the value of trigonometric functions involving half-angles, whether the original angle is known or not.

Section Exercises

Licenses & Attributions

Cc licensed content, original.

• Precalculus. Provided by: OpenStax Authored by: OpenStax College. Located at: https://cnx.org/contents/ [email protected] :1/Preface. License: CC BY: Attribution .

Please add a message.

Message received. Thanks for the feedback.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

13 Double-Angle, Half-Angle, and Reduction Formulas

Learning objectives.

In this section, you will:

• Use double-angle formulas to find exact values.
• Use double-angle formulas to verify identities.
• Use reduction formulas to simplify an expression.
• Use half-angle formulas to find exact values.

Using Double-Angle Formulas to Find Exact Values

Using the Pythagorean properties, we can expand this double-angle formula for cosine and get two more variations. The first variation is:

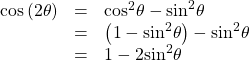
The second variation is:

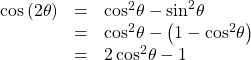
Double-Angle Formulas

The double-angle formulas are summarized as follows:

Given the tangent of an angle and the quadrant in which it is located, use the double-angle formulas to find the exact value.

• Draw a triangle to reflect the given information.
• Determine the correct double-angle formula.
• Substitute values into the formula based on the triangle.

Using a Double-Angle Formula to Find the Exact Value Involving Tangent

Now we can draw a triangle similar to the one shown in (Figure 2) .

Again, substitute the values of the sine and cosine into the equation, and simplify.

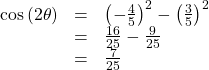
Using the Double-Angle Formula for Cosine without Exact Values

This example illustrates that we can use the double-angle formula without having exact values. It emphasizes that the pattern is what we need to remember and that identities are true for all values in the domain of the trigonometric function.

Using Double-Angle Formulas to Verify Identities

Establishing identities using the double-angle formulas is performed using the same steps we used to derive the sum and difference formulas. Choose the more complicated side of the equation and rewrite it until it matches the other side.

Using the Double-Angle Formulas to Verify an Identity

Verify the following identity using double-angle formulas:

We will work on the right side of the equal sign and rewrite the expression until it matches the left side.

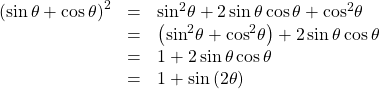
This process is not complicated, as long as we recall the perfect square formula from algebra:

Verifying a Double-Angle Identity for Tangent

Verify the identity:

In this case, we will work with the left side of the equation and simplify or rewrite until it equals the right side of the equation.

Here is a case where the more complicated side of the initial equation appeared on the right, but we chose to work the left side. However, if we had chosen the left side to rewrite, we would have been working backwards to arrive at the equivalency. For example, suppose that we wanted to show

Let’s work on the right side.

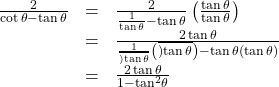
When using the identities to simplify a trigonometric expression or solve a trigonometric equation, there are usually several paths to a desired result. There is no set rule as to what side should be manipulated. However, we should begin with the guidelines set forth earlier.

Use Reduction Formulas to Simplify an Expression

The double-angle formulas can be used to derive the reduction formulas , which are formulas we can use to reduce the power of a given expression involving even powers of sine or cosine. They allow us to rewrite the even powers of sine or cosine in terms of the first power of cosine. These formulas are especially important in higher-level math courses, calculus in particular. Also called the power-reducing formulas, three identities are included and are easily derived from the double-angle formulas.

The last reduction formula is derived by writing tangent in terms of sine and cosine:

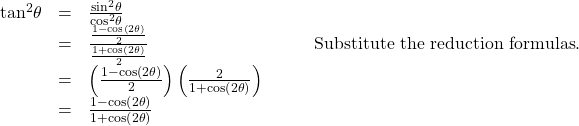
Reduction Formulas

The reduction formulas are summarized as follows:

Writing an Equivalent Expression Not Containing Powers Greater Than 1

We will apply the reduction formula for cosine twice.

The solution is found by using the reduction formula twice, as noted, and the perfect square formula from algebra.

Using the Power-Reducing Formulas to Prove an Identity

Use the power-reducing formulas to prove

We will work on simplifying the left side of the equation:

Note that in this example, we substituted

Using Half-Angle Formulas to Find Exact Values

The half-angle formula for sine is derived as follows:

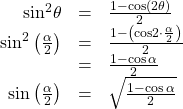
To derive the half-angle formula for cosine, we have

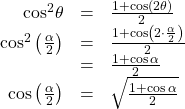
For the tangent identity, we have

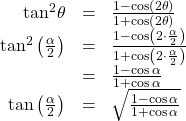
Half-Angle Formulas

The half-angle formulas are as follows:

Using a Half-Angle Formula to Find the Exact Value of a Sine Function

Remember that we can check the answer with a graphing calculator.

Given the tangent of an angle and the quadrant in which the angle lies, find the exact values of trigonometric functions of half of the angle.

• Draw a triangle to represent the given information.
• Determine the correct half-angle formula.

Finding Exact Values Using Half-Angle Identities

Finding the Measurement of a Half Angle

Access these online resources for additional instruction and practice with double-angle, half-angle, and reduction formulas.

• Double-Angle Identities
• Half-Angle Identities

Key Equations

Key concepts.

• Double-angle identities are derived from the sum formulas of the fundamental trigonometric functions: sine, cosine, and tangent. See (Figure) , (Figure) , (Figure) , and (Figure) .
• Reduction formulas are especially useful in calculus, as they allow us to reduce the power of the trigonometric term. See (Figure) and (Figure) .
• Half-angle formulas allow us to find the value of trigonometric functions involving half-angles, whether the original angle is known or not. See (Figure) , (Figure) , and (Figure) .

Section Exercises

Use the Pythagorean identities and isolate the squared term.

For the following exercises, find the values of the six trigonometric functions if the conditions provided hold.

For the following exercises, simplify to one trigonometric expression.

For the following exercises, find the exact value using half-angle formulas.

For the following exercises, use (Figure 5) to find the requested half and double angles.

For the following exercises, simplify each expression. Do not evaluate.

For the following exercises, prove the given identity.

For the following exercises, rewrite the expression with an exponent no higher than 1.

For the following exercises, reduce the equations to powers of one, and then check the answer graphically.

For the following exercises, prove the identities.

Trigonometry Copyright © 2015 by OpenStax is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

• Anatomy & Physiology
• Astrophysics
• Earth Science
• Environmental Science
• Organic Chemistry
• Precalculus
• Trigonometry
• English Grammar
• U.S. History
• World History

... and beyond

• Socratic Meta
• Featured Answers

• Half-Angle Identities

Key Questions

Common Half angle identity: 1. #sin a = 2 sin (a/2)* cos (a/2)#

Half angle Identities in term of t = tan a/2. 2. #sin a = (2t)/(1 + t^2)#

3. #cos a = (1 - t^2)/(1 + t^2)#

• #tan a = (2t)/(1 - t^2).#

Use of half angle identities to solve trig equations.

Example. Solve #cos x + 2*sin x = 1 + tan (x/2).# Solution. Call #t = tan (x/2)# . Use half angle identities (2) and (3) to transform the equation.

#(1 - t^2)/4 + (1 + t^2)/4 = 1 + t.#

#1 - t^2 + 4t = (1 + t)(1 + t^2)#

#t^3 + 2t^2 - 3t = t*(t^2 + 2t - 3) = 0.#

Next, solve the #3# basic trig equations: #tan (x/2) = t = 0; tan (x/2) = -3;# and #tan (x/2) = 1.#

• Google Apps™

What educators are saying

Also included in.

Description

Due to the length of this Trigonometry Unit Bundle , it is divided into two parts with two unit tests. In addition to the unit tests, each part includes guided notes, homework assignments, quizzes, and study guides to cover the following topics:

Unit 12 Part I:

• Pythagorean Theorem

• Special Right Triangles

• Trigonometric Functions (sin, cos, tan, csc, sec, cot)

• Finding Side and Angle Measures

• Applications: Angle of Elevation and Depression

• Angles in Standard Position

• Converting between Degrees and Radians

• Coterminal and Reference Angles

• Trigonometric Functions in the Coordinate Plane

• The Unit Circle

• Law of Sines

• Law of Cosines

• Area of Triangles

• Applications of Law of Sines, Law of Cosines, and Area

Unit 12 Part II:

• Graphing Trigonometric Functions

• Trigonometric Identities

• Sum and Difference of Angle Identities

• Double-Angle and Half-Angle Identities

• Solving Trigonometric Equations

ADDITIONAL COMPONENTS INCLUDED:

(1) Links to Instructional Videos: Links to videos of each lesson in the unit are included. Videos were created by fellow teachers for their students using the guided notes and shared in March 2020 when schools closed with no notice.  Please watch through first before sharing with your students. Many teachers still use these in emergency substitute situations. (2) Editable Assessments: Editable versions of each quiz and the unit test are included. PowerPoint is required to edit these files. Individual problems can be changed to create multiple versions of the assessment. The layout of the assessment itself is not editable. If your Equation Editor is incompatible with mine (I use MathType), simply delete my equation and insert your own.

(3) Google Slides Version of the PDF: The second page of the Video links document contains a link to a Google Slides version of the PDF. Each page is set to the background in Google Slides. There are no text boxes;  this is the PDF in Google Slides.  I am unable to do text boxes at this time but hope this saves you a step if you wish to use it in Slides instead! 

This resource is included in the following bundle(s):

Algebra 2 Curriculum

More Algebra 2 Units:

Unit 1 – Equations and Inequalities

Unit 2 – Linear Functions and Systems

Unit 3 – Parent Functions and Transformations

Unit 4 – Solving Quadratics and Complex Numbers

Unit 5 – Polynomial Functions

Unit 6 – Radical Functions

Unit 7 – Exponential and Logarithmic Functions

Unit 8 – Rational Functions

Unit 9 – Conic Sections

Unit 10 – Sequences and Series

Unit 11 – Probability and Statistics

LICENSING TERMS: This purchase includes a license for one teacher only for personal use in their classroom. Licenses are non-transferable , meaning they can not be passed from one teacher to another. No part of this resource is to be shared with colleagues or used by an entire grade level, school, or district without purchasing the proper number of licenses. If you are a coach, principal, or district interested in transferable licenses to accommodate yearly staff changes, please contact me for a quote at [email protected].

COPYRIGHT TERMS: This resource may not be uploaded to the internet in any form, including classroom/personal websites or network drives, unless the site is password protected and can only be accessed by students.

© All Things Algebra (Gina Wilson), 2012-present

Questions & Answers

All things algebra.

• We're hiring
• Help & FAQ
• Privacy policy
• Student privacy
• Terms of service
• Tell us what you think

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Precalculus

Course: precalculus   >   unit 2.

• Trig angle addition identities
• Using the cosine angle addition identity

Using the cosine double-angle identity

• Using the trig angle addition identities
• Proof of the sine angle addition identity
• Proof of the cosine angle addition identity
• Proof of the tangent angle sum and difference identities

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

Half Angle Calculator

Trigonometric functions, half-angle trig identities, example: using the half-angle calculator.

Welcome to Omni's half-angle calculator , where we'll study half-angle trig identities . The double angle formulas let us easily find the functions of twice the angle. Here, we'd like to do the same, but instead of multiplying the angle by two, we'll divide it . In fact, the main tool to find the sin, cos, and tan half-angle formulas are the power reducing identities .

But let's not get ahead of ourselves! There's more than enough time in the upcoming sections to go through it all slowly and in detail .

We hope you're ready and fully awake because it's time to begin !

Triangles are the simplest geometric objects we can construct. They have three sides, three angles, and that's basically all there is to them . Arguably, we can't have a polygon that has two, not to mention one side. So since triangles are that easy, it should be quite simple to understand them , right?

In some sense, it is indeed the case . For example, there are quite a few ways to find the area of a triangle. Although not all of them are pretty (check out Heron's formula calculator , for instance), there are times when each can be useful .

Furthermore, as the simplest polygons, triangles have been studied thoroughly since ancient times (remember Pythagoras?). Well, he was not the first, nor the last to commit his life to them.) After all, we can divide every polygon into triangles (e.g., by drawing a few diagonals), so if we understand the basic object, we should be able to understand all the others.

Trigonometry might just be the most useful tool in triangle studies. The idea behind it is to relate the side lengths to the inside angles. After all, you can easily see that if you have a triangle and increase one of its angles, then the sides must change accordingly . It turns out that the " accordingly " can be translated into some really nice functions. Check the trigonometric functions calculator to learn more!

There is only one right way to start talking about trigonometric functions - the right triangles (pun fully intended). Angle-wise, they are the easy case: we know that one angle must be 90 degrees, so that leaves us with only two to worry about . We define the trigonometric functions by the formulas listed below:

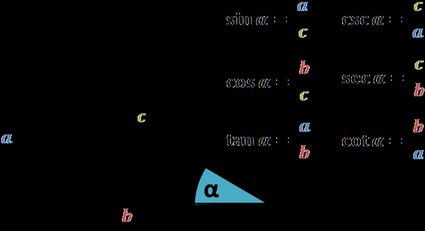
Note that we (and the half-angle identities calculator) limit ourselves to studying the sine, cosine, and tangent since the others are not as common in applications and textbooks.

There is, however, one significant drawback to the definitions above: the angle α must be between 0 and 90 degrees (or between 0 and π/2 radians) simply because it's a right triangle. Nevertheless, we can extend the definitions to any real value (even negative) by translating it all into a two-dimensional plane.

Let A = (x, y) be a point on the plane and denote by α the angle going counterclockwise from the positive half of the horizontal axis and the line segment connecting (0, 0) and A . (Observe how we said that α goes from one line to the other and not that it is between them. Because of that, we often call α a directed angle .)

Clearly, such an angle can be larger than 90 degrees. Even better - it can be larger than the full 360 degrees : it can make one full circle, and from 360 upwards begin its second lap. Also, since we've defined α to be directed, we can now have negative angles by simply going the other way, i.e., clockwise instead of counterclockwise.

For such angles, we extend the definitions of trigonometric functions from above by substituting in the formulas above a for y , b for x , and c for √(x² + y²) (the distance from (0, 0) to A ).

Alright, we hope that we've managed to convince you that trigonometric functions are useful . It may take a week or two to befriend them, but that moment is sure to come. Before that happens, however, let's mention some nice identities that use them. Needless to say, we'll focus on the tan, sin, and cos half-angle formulas .

In trigonometry, once we become familiar with the functions, the next step is to study the relations between them . It turns out that not only does, say, sine describe the ratio of a triangle's sides, but it is also connected to the cosine by nice and useful formulas .

The study of trigonometric identities and equations could easily fill a whole book or two. As a small encouragement to delve into the topic, let's mention two that appear quite often when dealing with triangles : the law of sines and the law of cosines.

We, however, have gathered here today to study the half-angle identities . And to understand where they come from, we'll use the so-called power reducing formulas . Below, we list the identities, but if you'd like to learn more about them, be sure to check out Omni's dedicated power reducing calculator .

A keen eye will observe that in each formula on the right, we have twice the angle that we have on the left . To be precise, the one on the left is half of the one on the right . And that's precisely what we need!

Firstly, take the top formula. We rewrite it with an angle of x 2 \frac{x}{2} 2 x ​ on the left and with x x x on the right (note that this notation must only keep the relation that one is half of the other ) and take the square root of both sides.

Observe that we need the ± \pm ± sign because of the properties of an even exponent. In practical calculations, the sign depends on which quadrant of the plane we are in with our angle.

The cos half-angle formula is obtained similarly:

Lastly, we take the tangent power reducing identity and do the same to get the tan half-angle formula . Note that equivalently, we could use the trigonometric identity tan ⁡ ( x ) = sin ⁡ ( x ) cos ⁡ ( x ) \tan\left(x\right) = \frac{\sin\left(x\right)}{\cos\left(x\right)} tan ( x ) = c o s ( x ) s i n ( x ) ​ .

Additionally, we can get two other tan half-angle formulas (which are also listed in the half-angle formula calculator) that have the advantage of not having the ± \pm ± sign. They come from using the double angle identities together with the tan ⁡ ( x ) = sin ⁡ ( x ) cos ⁡ ( x ) \tan\left(x\right) = \frac{\sin\left(x\right)}{\cos\left(x\right)} tan ( x ) = c o s ( x ) s i n ( x ) ​ formula and the Pythagorean identity of sin ⁡ 2 ( x ) + cos ⁡ 2 ( x ) = 1 \sin^2\left(x\right) + \cos^2\left(x\right) = 1 sin 2 ( x ) + cos 2 ( x ) = 1 . Indeed, on the one hand, we have

and on the other hand, similarly,

Aaand with that, we declare the end of theory for this article. After all this time spent reading through formulas, it's time for some numeric examples , and that's what the next section is all about!

Finally, your biggest dream has come true - you bought yourself a little hut in the mountains ! Well, it's not really a hut just yet, so far it's only a piece of land that you'll be building on, but it's most certainly a start. And after consulting our time value of money calculator , you've decided that it's the best form of investment.

You've taken social distancing to the next level and chosen an area far away from civilization . Unfortunately, this means that even before you let in a crew to put down some concrete foundations, you have to make sure that the machinery can get there safely . In particular, you need to prepare a stable driveway , at least a gravel one. There will come a time to upgrade it to asphalt, but for now, it will have to do .

There is one place that requires some extra attention - a 30 -degree slope that is a serious obstacle for heavier construction equipment. However, the crew tells you that if only you could flatten it out to half that, then it should be fine .

Wait, did anyone mention halving an angle ? Now, this should be a piece of cake for the half-angle calculator !

For precise data of what, where, and how you should flatten, you need to do some calculations about the slope . For that reason you can head to our slope calculator where we explained it in detail. To find gradient of a slope, it'd be useful to know the trigonometric functions of the angle you're dealing with. (After all, we can think of the slope as the hypotenuse of a large right triangle.) Of course, we could just Google the data, but where's the fun in that ? Answer: the fun is in using the half-angle identities calculator !

Let's break it down into a simple step-by-step solution/instruction .

• We know that the slope is at a 30 -degree angle, and we'd like to reduce it to half that . To find the trigonometric functions in this case, it is enough to enter into the half-angle calculator the data that we begin with .
• Under " Angle " we input the 30 degrees, and the moment we do, the tool will spit out the answer , both for the full angle and the halved one.
• Note also that 30 is a special case of a right triangle, so the half-angle calculator will show you the precise values of the trigonometric functions before we round them up, i.e., in the form of a fraction with square roots.

Just on the side, let us now see how to use the half-angle trig identities to find the answer by hand . So grab a piece of paper, and let's get to it !

First of all, let's begin with the obvious : half of 30 degrees is 15 degrees. This means that our half-angle is in the first quadrant (because it's between 0 and 90 degrees). This further translates to the sine, cosine, and tangent being positive . Therefore, for the sin, cos, and tan half-angle formulas, we'll use the identities with a + + + where we had the ± \pm ± sign.

We'll begin with sine . Recall that cos ⁡ ( 30 ° ) = 3 2 \cos\left(30 \degree\right) = \frac{\sqrt{3}}{2} cos ( 30° ) = 2 3 ​ ​ , so:

Next, the cos half-angle formula gives:

Lastly, from the tan half-angle formula , we obtain:

And there it is! We now have all the information needed to get to work and reduce that angle of ascension. Or... Maybe first, a short hike up the mountain? The job can wait an hour or two, can't it?

How do you calculate the sine of a half angle?

To calculate the sine of a half angle sin(x/2) , follow these short steps:

Write down the angle x and replace it within the sine of half angle formula :

sin(x/2) = ± √[(1 - cos x)/2] .

Determine the sign using the half angle:

• Positive (+) if the half angle lies on the 1st or 2nd quadrants ; or
• Negative (-) if it lies on the 3rd or 4th quadrants .

What is cos(15°)?

√[(2 + √3) / 2] . Since 15° is half of 30° , you can use the half-angle formula for cosine to find the cosine of 15° :

cos(30°/2) = ±√[(1 + cos 30°)/2] = √[(2 + √3) / 2] .

How do you determine the sign in half-angle trigonometric identities?

The sign of trigonometric identities involving half-angles depends on the quadrant where the half-angle is and the trigonometric function:

• Positive if half angle lies on 1st or 2nd quadrants . Negative otherwise.
• Positive if half angle lies on 1st or 4th quadrants . Negative otherwise.
• Positive if half angle lies on 1st or 3rd quadrants . Negative otherwise.

Is cos(x/2) the same as cos(x)/2?

No . The expression cos(x/2) refers to the cosine of half an angle x , while cos(x)/2 is half the cosine of x . To modify the argument of a trigonometric expression, you need to use trigonometric identities, such as the cosine of half an angle:

cos(x/2) = ±√[(1 + cos 30°)/2] .

• Trig Identities Calculator

Distributive property

Expanded form, plastic footprint.

• Biology (101)
• Chemistry (100)
• Construction (145)
• Conversion (295)
• Ecology (30)
• Everyday life (262)
• Finance (571)
• Health (440)
• Physics (511)
• Sports (105)
• Statistics (184)
• Other (183)
• Discover Omni (40)

• Skip to main content

PAYMENT PLANS ARE NOW AVAILABLE • VISIT THE SHOP TO LEARN MORE!

All Things Algebra®

Algebra 2 Unit 12: Trigonometry

This unit includes 96 pages of guided notes, homework assignments, three quizzes, two study guides, and two unit tests that cover the topics listed in the description below.

• Description
• Additional Information
• What Educators Are Saying

This unit contains the following topics:

Part I: • Pythagorean Theorem • Special Right Triangles • Trigonometric Functions (sin, cos, tan, csc, sec, cot) • Finding Side and Angle Measures • Applications: Angle of Elevation and Depression • Angles in Standard Position • Converting between Degrees and Radians • Coterminal and Reference Angles • Trigonometric Functions in the Coordinate Plane • The Unit Circle • Law of Sines • Law of Cosines • Area of Triangles • Applications of Law of Sines, Law of Cosines, and Area

Unit 12 Part II: • Graphing Trigonometric Functions • Trigonometric Identities • Sum and Difference of Angle Identities • Double-Angle and Half-Angle Identities • Solving Trigonometric Equations

Note:  Due to the length of this unit, it is divided into two parts with two unit tests.

This unit does not contain activities.

This is the guided notes, homework assignments, quizzes, study guide, and unit test only.  For suggested activities to go with this unit, check out the ATA Activity Alignment Guides .

This resource is included in the following bundle(s):

Algebra 2 Curriculum

License Terms:

This purchase includes a single non-transferable license, meaning it is for one teacher only for personal use in their classroom and can not be passed from one teacher to another.  No part of this resource is to be shared with colleagues or used by an entire grade level, school, or district without purchasing the proper number of licenses.  A t ransferable license is not available for this resource.

Copyright Terms:

No part of this resource may be uploaded to the internet in any form, including classroom/personal websites or network drives, unless the site is password protected and can only be accessed by students.

What standards is this curriculum aligned to?

What format are the files in, will i have access to materials if they are updated, are answer keys included, are videos included.

All things algebra is the best math creator in my opinion, I will continuously use and purchase the products! Students find them easy to use, engaging, and fun! I love the opportunities for differentiation as well.

I'm teaching a Pre-Calculus class but with students whose skill level is slightly below average (and most of whom won't be on a Calculus track for senior year/college), and using this Alg. II unit for the Trigonometry lessons has been really helpful. It breaks it down for them and covers all of the basics/necessities without getting too "into the weeds" on the parts that I knew they would struggle more with.

This is a great bridge to my textbook that is a little high for the average student. My lower level classes, this is the perfect fit in not set up and work. The topic examples are on target for the standards as well.

• + ACCUPLACER Mathematics
• + ACT Mathematics
• + AFOQT Mathematics
• + ALEKS Tests
• + ASVAB Mathematics
• + ATI TEAS Math Tests
• + Common Core Math
• + DAT Math Tests
• + FSA Tests
• + FTCE Math
• + GED Mathematics
• + Georgia Milestones Assessment
• + GRE Quantitative Reasoning
• + HiSET Math Exam
• + HSPT Math
• + ISEE Mathematics
• + PARCC Tests
• + Praxis Math
• + PSAT Math Tests
• + PSSA Tests
• + SAT Math Tests
• + SBAC Tests
• + SIFT Math
• + SSAT Math Tests
• + STAAR Tests
• + TABE Tests
• + TASC Math
• + TSI Mathematics
• + ACT Math Worksheets
• + Accuplacer Math Worksheets
• + AFOQT Math Worksheets
• + ALEKS Math Worksheets
• + ASVAB Math Worksheets
• + ATI TEAS 6 Math Worksheets
• + FTCE General Math Worksheets
• + GED Math Worksheets
• + 3rd Grade Mathematics Worksheets
• + 4th Grade Mathematics Worksheets
• + 5th Grade Mathematics Worksheets
• + 6th Grade Math Worksheets
• + 7th Grade Mathematics Worksheets
• + 8th Grade Mathematics Worksheets
• + 9th Grade Math Worksheets
• + HiSET Math Worksheets
• + HSPT Math Worksheets
• + ISEE Middle-Level Math Worksheets
• + PERT Math Worksheets
• + Praxis Math Worksheets
• + PSAT Math Worksheets
• + SAT Math Worksheets
• + SIFT Math Worksheets
• + SSAT Middle Level Math Worksheets
• + 7th Grade STAAR Math Worksheets
• + 8th Grade STAAR Math Worksheets
• + THEA Math Worksheets
• + TABE Math Worksheets
• + TASC Math Worksheets
• + TSI Math Worksheets
• + AFOQT Math Course
• + ALEKS Math Course
• + ASVAB Math Course
• + ATI TEAS 6 Math Course
• + CHSPE Math Course
• + FTCE General Knowledge Course
• + GED Math Course
• + HiSET Math Course
• + HSPT Math Course
• + ISEE Upper Level Math Course
• + SHSAT Math Course
• + SSAT Upper-Level Math Course
• + PERT Math Course
• + Praxis Core Math Course
• + SIFT Math Course
• + 8th Grade STAAR Math Course
• + TABE Math Course
• + TASC Math Course
• + TSI Math Course
• + Number Properties Puzzles
• + Algebra Puzzles
• + Geometry Puzzles
• + Intelligent Math Puzzles
• + Ratio, Proportion & Percentages Puzzles
• + Other Math Puzzles

Unlocking Trigonometric Secrets: A Comprehensive Guide to Double-Angle and Half-Angle Formulas

Understanding double-angle and half-angle formulas is essential for solving advanced problems in trigonometry. These formulas are pivotal in simplifying and solving trigonometric expressions and equations involving angles that are multiples or submultiples of a given angle.

Step-by-step Guide to Understanding Double-Angle and Half-Angle Formulas

Here is a step-by-step guide to understanding double-Angle and half-Angle formulas:

Double Angle Formulas

Double angle formulas are used to express trigonometric ratios of double angles (\(2θ\)) in terms of trigonometric ratios of single angles (\(θ\)). These are particularly useful in integration, differentiation, and when solving trigonometric equations.

• \(sin(2θ)=2sin(θ)cos(θ)\)
• \(cos(2θ)=cos^{2}(θ)−sin^{2}(θ)\)
• \(cos(2θ)=1−2sin^{2}(θ)\)
• \(cos(2θ)=2cos^{2}(θ)−1\)
• \(tan(2θ)=\frac{2tan(θ)​}{1−tan^2(θ)}\)

These formulas can be derived from the sum formulas for sine and cosine. For example, the sine double angle formula can be derived from the sine addition formula \(sin(α+β)\).

Half-Angle Formulas

Half-angle formulas are used to find the trigonometric ratios of half an angle (\(\frac{θ}{2}\)). These are useful when dealing with power reduction or solving trigonometric equations that involve half angles.

• \(sin \ (\frac{θ}{2}​)=±\sqrt{\frac{1−cos(θ)}{2}​​}\)
• \(cos \ (\frac{θ}{2}​)=±\sqrt{\frac{1+cos(θ)}{2}​​}\)
• \(tan \ (\frac{θ}{2}​)=±\sqrt{\frac{1−cos(θ)​​}{1+cos(θ)}}\)
• \(tan \ (\frac{θ}{2}​)=\frac{sin(θ)​}{1+cos(θ)}\)
• \(tan \ (\frac{θ}{2}​)=\frac{1−cos(θ)​}{sin(θ)}\)

The choice of a positive or negative square root in the half-angle formulas depends on the quadrant in which \((\frac{θ}{2}​)​\)​ lies.

Applying These Formulas

To effectively use these formulas, follow these steps:

• Identify the Need : Recognize when a double-angle or half-angle formula is useful. This is typically when you’re dealing with trigonometric expressions involving \(2θ\) or \((\frac{θ}{2}​)​\).
• Select the Appropriate Formula : Choose the formula that best simplifies the given problem. For instance, in a problem involving \(sin(2θ)\), use the sine double angle formula.
• Substitute and Simplify : Replace the double or half-angle expression with its equivalent from the formula. Then, simplify the expression further if needed.
• Solve : If you’re solving an equation, proceed to find the values of \(θ\) after applying the formula.

Understanding and applying double-angle and half-angle formulas is key to simplifying complex trigonometric expressions. These formulas not only offer a more profound understanding of trigonometry but also are essential tools in calculus and physics.

by: Effortless Math Team about 7 months ago (category: Articles )

Effortless Math Team

Related to this article, more math articles.

• How to Find Volume and Surface Area of Cubes? (+FREE Worksheet!)
• How to Write a Formula for a Recursive Sequence
• How to Find Complementary and Supplementary Angles? (+FREE Worksheet!)
• Algebra Puzzle – Challenge 58
• How to Use Models to Multiply Two Fractions?
• 10 Most Common PERT Math Questions
• Overview of Middle-Level SSAT Mathematics Test
• 8 Ways to Get Your Kids To Love Math
• The Ultimate 6th Grade MEA Math Course (+FREE Worksheets)
• 5 Best ASVAB Math Study Guides

What people say about "Unlocking Trigonometric Secrets: A Comprehensive Guide to Double-Angle and Half-Angle Formulas - Effortless Math: We Help Students Learn to LOVE Mathematics"?

No one replied yet.

Leave a Reply Cancel reply

You must be logged in to post a comment.

Algebra I Study Guide A Comprehensive Review and Step-By-Step Guide to Preparing for Algebra I

Oar math study guide 2020 – 2021 a comprehensive review and step-by-step guide to preparing for the oar math, psat math study guide 2020 – 2021 a comprehensive review and step-by-step guide to preparing for the psat math, act math study guide 2020 – 2021 a comprehensive review and step-by-step guide to preparing for the act math, accuplacer math study guide 2020 – 2021 a comprehensive review and step-by-step guide to preparing for the accuplacer math, aleks math study guide 2020 – 2021 a comprehensive review and step-by-step guide to preparing for the aleks math, pre-algebra study guide 2020 – 2021 a comprehensive review and step-by-step guide to preparing for the pre-algebra, asvab math study guide 2020 – 2021 a comprehensive review and step-by-step guide to preparing for the asvab math, afoqt math study guide 2020 – 2021 a comprehensive review and step-by-step guide to preparing for the afoqt math, hiset math study guide 2020 – 2021 a comprehensive review and step-by-step guide to preparing for the hiset math, chspe math study guide 2020 – 2021 a comprehensive review and step-by-step guide to preparing for the chspe math, tsi math study guide 2020 – 2021 a comprehensive review and step-by-step guide to preparing for the tsi math, tabe 11 & 12 math study guide 2020 – 2021 for level d a comprehensive review and step-by-step guide to preparing for the tabe math, ftce math study guide 2020 – 2021 a comprehensive review and step-by-step guide to preparing for the ftce general knowledge math, ged math study guide 2020 – 2021 a comprehensive review and step-by-step guide to preparing for the ged math.

• ATI TEAS 6 Math
• ISEE Upper Level Math
• SSAT Upper-Level Math
• Praxis Core Math
• 8th Grade STAAR Math

Limited time only!

Save Over 45 %

It was $89.99 now it is $49.99

Login and use all of our services.

Effortless Math services are waiting for you. login faster!

Register Fast!

Password will be generated automatically and sent to your email.

After registration you can change your password if you want.

• Math Worksheets
• Math Courses
• Math Topics
• Math Puzzles
• Math eBooks
• GED Math Books
• HiSET Math Books
• ACT Math Books
• ISEE Math Books
• ACCUPLACER Books
• Premium Membership
• Youtube Videos

Effortless Math provides unofficial test prep products for a variety of tests and exams. All trademarks are property of their respective trademark owners.

• Bulk Orders
• Refund Policy

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.6: Half Angle Identities

• Last updated
• Save as PDF
• Page ID 61256

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Apply the half-angle identities to expressions, equations and other identities.
• Use the half-angle identities to find the exact value of trigonometric functions for certain angles.

Power Reduction and Half Angle Identities

Another use of the cosine double angle identities is to use them in reverse to rewrite a squared sine or cosine in terms of the double angle. Starting with one form of the cosine double angle identity:

\[\cos (2\alpha )=2\cos ^{2} (\alpha )-1\nonumber\]Isolate the cosine squared term \[\cos (2\alpha )+1=2\cos ^{2} (\alpha )\nonumber\] Add 1 \[\cos ^{2} (\alpha )=\dfrac{\cos (2\alpha )+1}{2}\nonumber\]Divide by 2 \[\cos ^{2} (\alpha )=\dfrac{\cos (2\alpha )+1}{2}\nonumber\] This is called a power reduction identity

Exercise \(\PageIndex{1}\)

Use another form of the cosine double angle identity to prove the identity \(\sin ^{2} (\alpha )=\dfrac{1-\cos (2\alpha )}{2}\).

\[\begin{array}{l} {\dfrac{1-\cos (2\alpha )}{2} } \\ {\dfrac{1-\left(\cos ^{2} (\alpha )-\sin ^{2} (\alpha )\right)}{2} } \\ {\dfrac{1-\cos ^{2} (\alpha )+\sin ^{2} (\alpha )}{2} } \\ {\dfrac{\sin ^{2} (\alpha )+\sin ^{2} (\alpha )}{2} } \\ {\dfrac{2\sin ^{2} (\alpha )}{2} =\sin ^{2} (\alpha )} \end{array}\nonumber\]

The cosine double angle identities can also be used in reverse for evaluating angles that are half of a common angle. Building from our formula \(\cos ^{2} (\alpha )=\dfrac{\cos (2\alpha )+1}{2}\), if we let \(\theta =2\alpha\), then \(\alpha =\dfrac{\theta }{2}\) this identity becomes \(\cos ^{2} \left(\dfrac{\theta }{2} \right)=\dfrac{\cos (\theta )+1}{2}\). Taking the square root, we obtain

\[\cos \left(\dfrac{\theta }{2} \right)=\pm \sqrt{\dfrac{\cos (\theta )+1}{2} }\nonumber\]where the sign is determined by the quadrant.

This is called a half-angle identity .

Exercise \(\PageIndex{2}\)

Use your results from the last Try it Now to prove the identity \(\sin \left(\dfrac{\theta }{2} \right)=\pm \sqrt{\dfrac{1-\cos (\theta )}{2} }\).

\[\begin{array}{l} {\sin ^{2} (\alpha )=\dfrac{1-\cos (2\alpha )}{2} } \\ {\sin (\alpha )=\pm \sqrt{\dfrac{1-\cos (2\alpha )}{2} } } \\ {\alpha =\dfrac{\theta }{2} } \\ {\sin \left(\dfrac{\theta }{2} \right)=\pm \sqrt{\dfrac{1-\cos \left(2\left(\dfrac{\theta }{2} \right)\right)}{2} } } \\ {\sin \left(\dfrac{\theta }{2} \right)=\pm \sqrt{\dfrac{1-\cos (\theta )}{2} } } \end{array}\nonumber\]

Half-Angle Identities

\[\cos \left(\dfrac{\theta }{2} \right)=\pm \sqrt{\dfrac{\cos (\theta )+1}{2} }\]

\[\sin \left(\dfrac{\theta }{2} \right)=\pm \sqrt{\dfrac{1-\cos (\theta )}{2} }\]

Power Reduction Identities

\[\cos ^{2} (\alpha )=\dfrac{\cos (2\alpha )+1}{2}\]

\[\sin ^{2} (\alpha )=\dfrac{1-\cos (2\alpha )}{2}\]

Since these identities are easy to derive from the double-angle identities, the power reduction and half-angle identities are not ones you should need to memorize separately.

Example \(\PageIndex{1}\)

Rewrite \(\cos ^{4} (x)\) without any powers.

\[\cos ^{4} (x)=\left(\cos ^{2} (x)\right)^{2}\nonumber\]Using the power reduction formula \[=\left(\dfrac{\cos (2x)+1}{2} \right)^{2}\nonumber\]Square the numerator and denominator \[=\dfrac{\left(\cos (2x)+1\right)^{2} }{4}\nonumber\]Expand the numerator \[=\dfrac{\cos ^{2} (2x)+2\cos (2x)+1}{4}\nonumber\]Split apart the fraction \[=\dfrac{\cos ^{2} (2x)}{4} +\dfrac{2\cos (2x)}{4} +\dfrac{1}{4}\nonumber\]Apply the formula above to \(\cos ^{2} (2x)\) \[\cos ^{2} (2x)=\dfrac{\cos (2\cdot 2x)+1}{2}\nonumber\] \[=\dfrac{\left(\dfrac{\cos (4x)+1}{2} \right)}{4} +\dfrac{2\cos (2x)}{4} +\dfrac{1}{4}\nonumber\]Simplify \[=\dfrac{\cos (4x)}{8} +\dfrac{1}{8} +\dfrac{1}{2} \cos (2x)+\dfrac{1}{4}\nonumber\]Combine the constants \[=\dfrac{\cos (4x)}{8} +\dfrac{1}{2} \cos (2x)+\dfrac{3}{8}\nonumber\]

Example \(\PageIndex{2}\)

Find an exact value for \(\cos \left(15{}^\circ \right)\).

Since 15 degrees is half of 30 degrees, we can use our result from above:

\[\cos (15{}^\circ )=\cos \left(\dfrac{30{}^\circ }{2} \right)=\pm \sqrt{\dfrac{\cos (30{}^\circ )+1}{2} }\nonumber\]

We can evaluate the cosine. Since 15 degrees is in the first quadrant, we need the positive result.

\[\sqrt{\dfrac{\cos (30{}^\circ )+1}{2} } =\sqrt{\dfrac{\dfrac{\sqrt{3} }{2} +1}{2} }\nonumber\] \[=\sqrt{\dfrac{\sqrt{3} }{4} +\dfrac{1}{2} }\nonumber\]

Exercise \(\PageIndex{3}\)

If \(\csc \left(x\right)=7\) and \(90{}^\circ <x<180{}^\circ\), then find exact values for (without solving for \(x\)):

a. \(\sin \left(\dfrac{x}{2} \right)\) b. \(\cos \left(\dfrac{x}{2} \right)\) c. \(\tan \left(\dfrac{x}{2} \right)\)

a. \(\sqrt{\dfrac{1}{2}+\dfrac{2 + \sqrt{7}}{7}}\) b. \(\sqrt{\dfrac{1}{2}-\dfrac{2 + \sqrt{7}}{7}}\) c. \(\dfrac{1}{7 - 4\sqrt{3}}\)

Important Topics of This Section

• Power reduction identity
• Half angle identity
• Using identities
• Simplify equations
• Prove identities
• Solve equations