High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Straight angle
Angles in parallel lines

Corresponding angles
Here you will learn about corresponding angles including how to recognize corresponding angles and apply this understanding to solve problems.
Students will first learn about corresponding angles as part of geometry in 8 th grade and expand their learning in high school.
Every week, we teach lessons on corresponding angles to students in schools and districts across the US as part of our online one-on-one math tutoring programs. On this page we’ve broken down everything we’ve learnt about teaching this topic effectively.
What are corresponding angles?
Corresponding angles occur when a transversal line crosses two parallel lines. The pairs of angles formed on the same side of the transversal and in the same relative position are called corresponding angles and are equal in size.
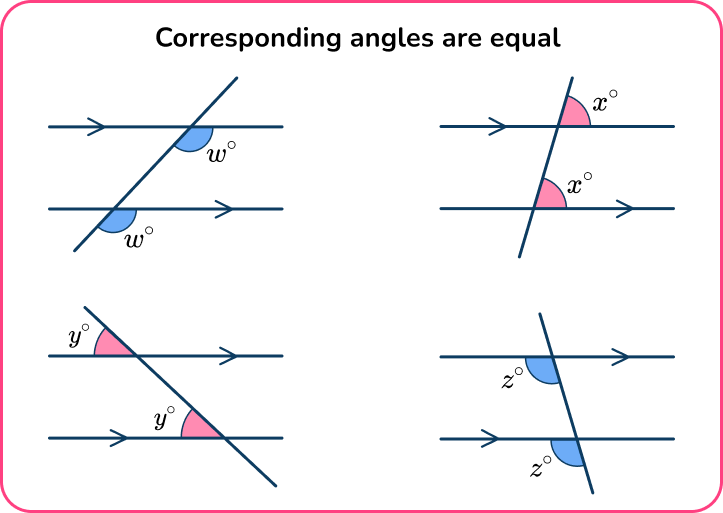
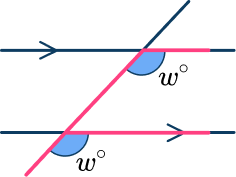
You can often spot corresponding angles by drawing an F shape.
Common Core State Standards
How does this relate to 8 th grade math and high school math?
- Grade 8 – Geometry (8.G.A.5) Use informal arguments to establish facts about the angle sum and exterior angle of triangles, about the angles created when parallel lines are cut by a transversal, and the angle-angle criterion for similarity of triangles. For example, arrange three copies of the same triangle so that the sum of the three angles appears to form a line, and give an argument in terms of transversals why this is so.
- High School – Geometry (HSG.CO.C.9) Prove theorems about lines and angles. Theorems include: vertical angles are congruent; when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent; points on a perpendicular bisector of a line segment are exactly those equidistant from the segment’s endpoints.
![geometry assignment identify each pair of angles as corresponding [FREE] Angles Check for Understanding Quiz (Grade 4)](https://thirdspacelearning.com/wp-content/uploads/2023/08/Angles-check-for-understanding-quiz-listing-image.png)
[FREE] Angles Check for Understanding Quiz (Grade 4)
Use this quiz to check your grade 4 students’ understanding of angles. 10+ questions with answers covering a range of 4th grade angles topics to identify areas of strength and support!
How to find corresponding angles
In order to find corresponding angles:
Identify two parallel lines that are intersected by a transversal.
Locate the angles that lie on the same side of the transversal and on different parallel lines.
Recognize that these pairs of angles are corresponding angles and are congruent.
Corresponding angles examples
Example 1: find the corresponding angles.
\overleftarrow{\,C}\overrightarrow{D\,} and \overleftarrow{\,E}\overrightarrow{H\,} are parallel lines.
Which angle is the corresponding angle to \angle ABC?
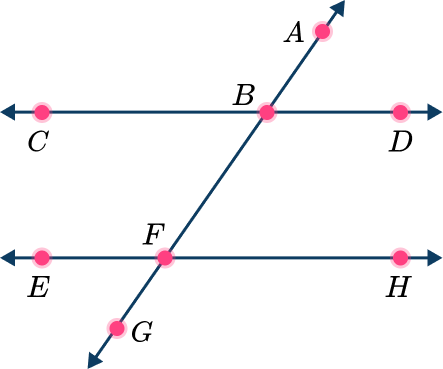
CD and EH are parallel lines. Line AG is the transversal.
2 Locate the angles that lie on the same side of the transversal and on different parallel lines.
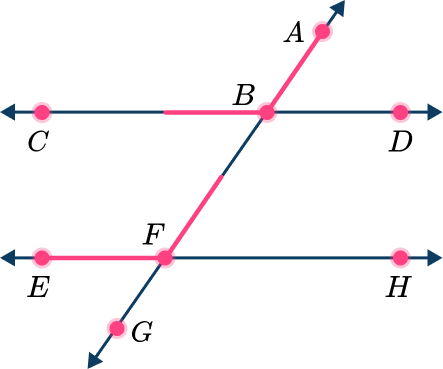
There are many pairs of corresponding lines, but the question asks which angle is a corresponding angle to \angle ABC. \angle BFE is on the same side of the transversal and on a different parallel line than \angle ABC.
3 Recognize that these pairs of angles are corresponding angles and are congruent.
\angle BFE and \angle ABC are corresponding angles.
Example 2: find pairs of corresponding angles
\overleftarrow{\,S}\overrightarrow{Y\,} and \overleftarrow{\,T}\overrightarrow{Z\,} are parallel lines.
Name all pairs of corresponding angles.
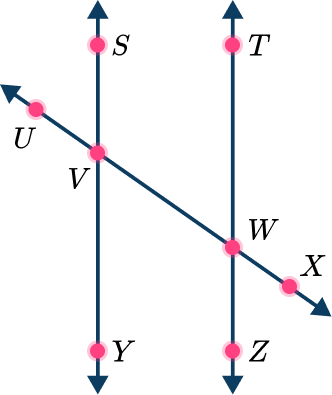
The two parallel lines are SY and TZ. Line UX is the transversal.
There are four pairs of angles that lie on the same side of the transversal and on different parallel lines. All 4 are pairs of corresponding angles.
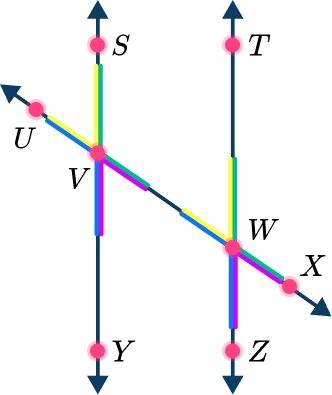
The pairs of corresponding angles are:
\angle SVW and \angle TWX
\angle SVU and \angle TWV
\angle UVY and \angle VWZ
\angle YVW and \angle ZWX
Example 3: corresponding angles in a real-world object
Look at the road intersections shown below. Which two letters represent corresponding angles?
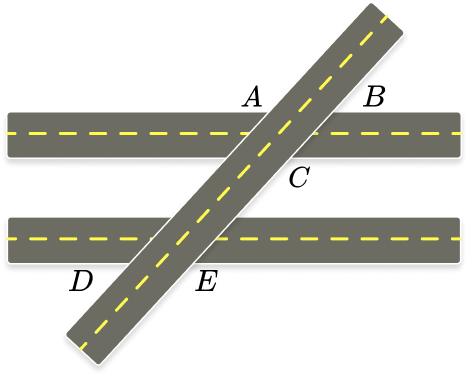
The two horizontal roads are parallel lines, and the diagonal road is the transversal.
C and E are the only letters on the same side of the transversal and on different parallel lines.
C and E are corresponding angles.
How to find the missing angle with corresponding angles
In order to find the missing angle with corresponding angles:
Highlight the angle(s) that you already know.
Use corresponding angles to find a missing angle.
Use basic angle facts if needed to calculate other missing angles.
Note: Steps 2 and 3 may be done in either order and may need to be repeated. Step 3 may not always be required.
Example 4: corresponding angles
Find the measure of the missing angle \theta. Justify your answer.
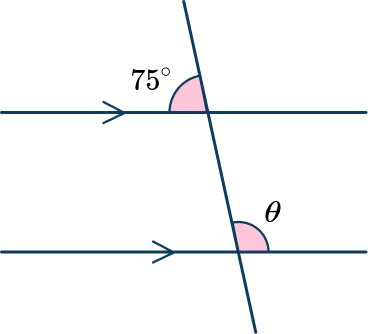
Here you can label the corresponding angle on the diagram as 75^{\circ}.
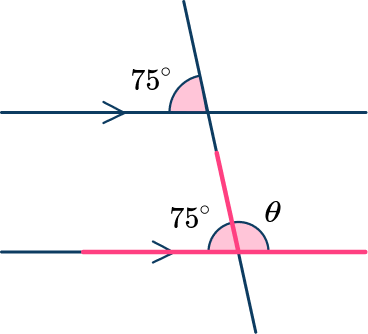
Here \theta is on a straight line with 75^{\circ}
\begin{aligned}\theta&=180^{\circ}-75^{\circ} \\\\ \theta&=105^{\circ}\end{aligned}
Example 5: corresponding angles
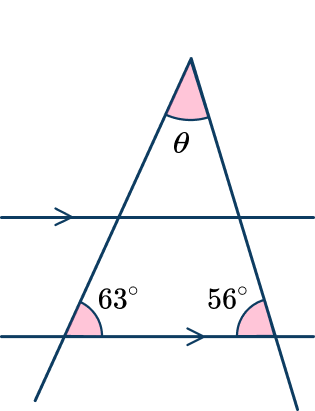
The new angles of 63^{\circ} and 56^{\circ} are corresponding angles to the original angles as shown above as they are on the same side of each transversal.
As the sum of angles in a triangle is 180^{\circ},
\begin{aligned}\theta&=180^{\circ}-\left(63^{\circ}+56^{\circ}\right) \\\\ \theta&=61^{\circ}\end{aligned}
Example 6: corresponding angles with algebra
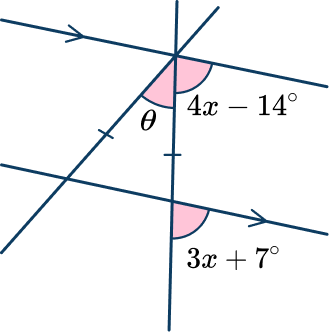
Here, you need to find the value for x to find the value of \theta.
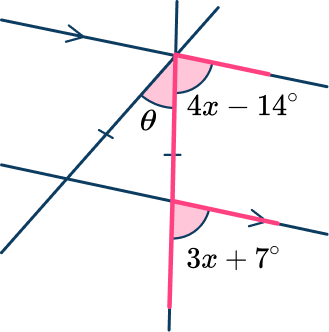
4 x-14 and 3 x+7 are corresponding angles. This allows you to find the value of x as the two angles are equal:
\begin{aligned}&4x-14=3 x+7 \\\\ &4x=3x+21 \\\\ &x=21^{\circ}\end{aligned}
As x=21^{\circ}, you have the two angles 4 x-14=3 x+7=70^{\circ}.
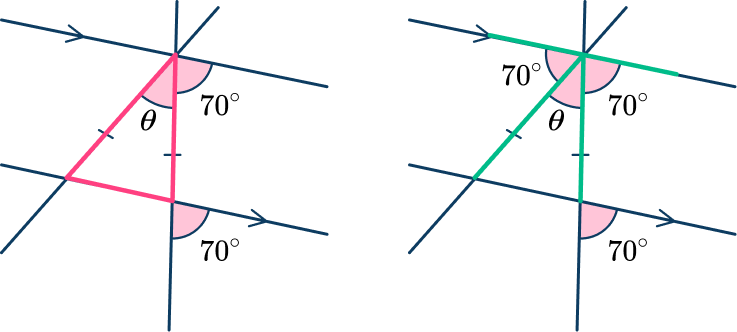
Here you can combine the fact that you have an isosceles triangle and the sum of angles on a straight line is 180^{\circ}.
As the triangle is isosceles with the base of the triangle on one parallel line, the angles on either side of the top vertex of the triangle are symmetrical (this can also be calculated using the alternate angle rule). These angles form a straight line. You can therefore find \theta \text{:}
\begin{aligned}\theta&=180-(70+70) \\\\ \theta&=40^{\circ}\end{aligned}
Teaching tips for corresponding angles
- Provide examples on student worksheets of corresponding angles alongside other types of angles, such as alternate interior angles or alternate exterior angles. This allows students to compare and contrast different angle relationships.
- Relate corresponding angles to real-life scenarios, such as the angles formed by intersecting streets, railway tracks, or architectural structures. This can help students understand the practical significance of corresponding angles
Easy mistakes to make
- Mixing up angle facts There are a lot of angle facts and it is easy to mistake alternate angles with corresponding angles. To prevent this from occurring, think about corresponding angles as being underneath the F shape.
- Using a protractor to measure an angle Using a protractor to find angle measures can be problematic. Most diagrams are not to scale, so using a protractor will not result in a correct answer unless it is a coincidence.
Related angles in parallel lines lessons
- Alternate interior angles theorem
- Parallel angles
- Same side interior angles
Practice corresponding angles questions
1. Which two angles are corresponding angles?
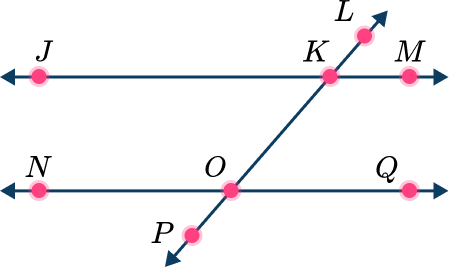
JKL and \angle LKM

\angle JKO and \angle KON
\angle MKO and \angle QOP

\angle MKO and \angle LKM
The only pair of angles listed that are on the same side of the traversal and on different parallel lines are \angle MKO and \angle QOP.
2. Find the measure of angle \theta.
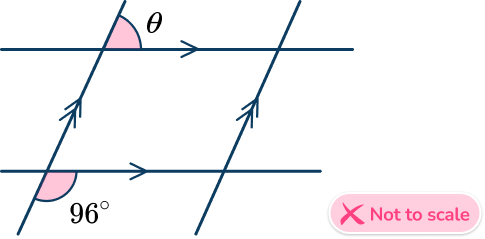
Using corresponding angles, you can see the angle 96^{\circ}.
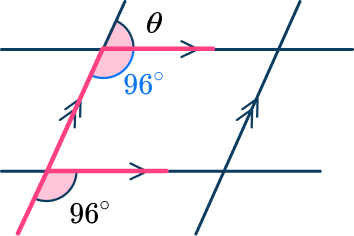
You can then use angles on a straight line:
3. Find the measure of \theta.
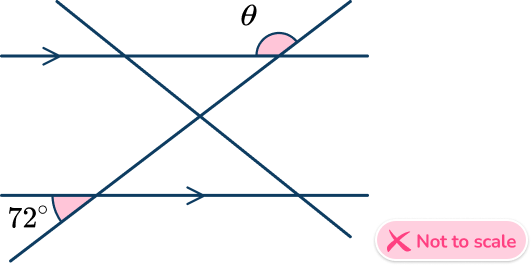
Using corresponding angles, you can see the angle 72^{\circ}.
4. Find the measure of angle \theta.
You start by calculating the missing angle in the triangle:
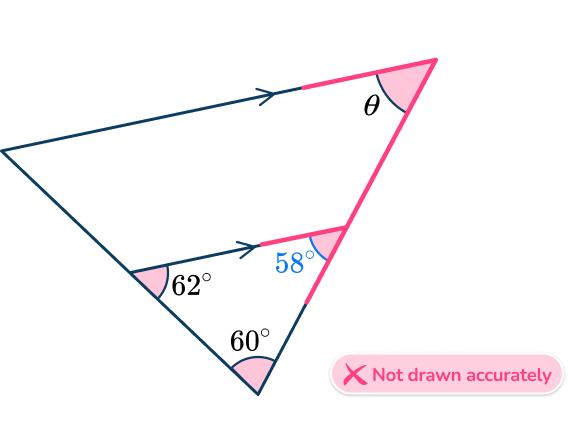
You can then use corresponding angles to see that \theta=58^{\circ}
5. Find the measure for angle \theta.
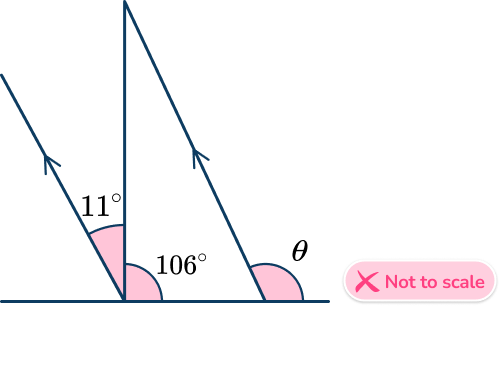
Using corresponding angles, you can see that \theta is corresponding to 106+11, therefore, \theta=106+11=115^{\circ}
6. By finding the measure of x, find the size of each of the corresponding angles labeled in the diagram.
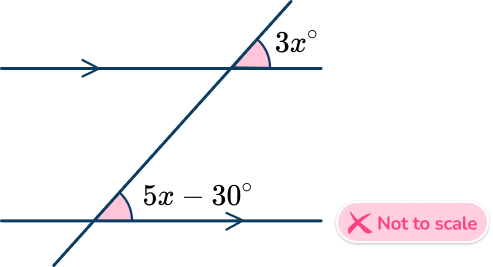
45^{\circ} and 45^{\circ}
45^{\circ} and 135^{\circ}
30^{\circ} and 20^{\circ}
50^{\circ} and 50^{\circ}
3x and 5 x-30 are corresponding angles and so are equal.
Therefore you can write 3 x=5 x-30.
You can then solve this:
Corresponding angles FAQs
Corresponding angles are angle pairs formed when a transversal intersects two parallel lines. Pairs of corresponding angles are located on the same side of the transversal but on different parallel lines, and they have equal measures.
1. Corresponding angles formed by parallel lines and transversals 2. Corresponding angles formed by non-parallel lines and transversals
The corresponding angle postulate states that when a transversal intersects two parallel lines, the corresponding angles formed are congruent (for example, ., they have equal measures).
The converse of the corresponding angles theorem states that if two lines are cut by a transversal and the corresponding angles are congruent, then the lines are parallel.
Corresponding angles are found on the same side of the transversal but on different parallel lines and have equal measures. Consecutive interior angles are located on the same side of the transversal and inside the intersecting lines, and are supplementary angles, meaning they add up to 180 degrees.
The next lessons are
- Quadrilateral
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!
Privacy Overview
Corresponding angles
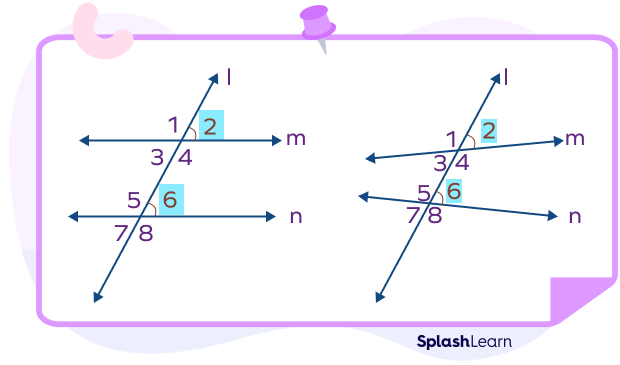
In geometry, corresponding angles are pairs of angles formed when a transversal intersects two lines. Refer to the figure below. The corresponding angles are the angles that lie on the same side of the transversal in matching corners. In other words, they occupy the same relative position in the figure. In a pair of corresponding angles, one is an exterior angle and one is an interior angle.
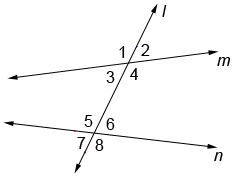
In the figure, transversal l intersects lines m and n. ∠1 and ∠5 are a pair of corresponding angles. Similarly, ∠2 and ∠6, ∠3 and 7, and ∠4 and ∠8 are also corresponding angles.
Corresponding angles can never be adjacent angles. If the angles are adjacent (touch), they are not corresponding angles. This also means that consecutive internal angles, such as angles 7 and 8, can never be corresponding angles.
Corresponding angles are just one type of angle pair. Alternate angles are another type of angle pair. In the figure, angles 6 and 3 are alternate angles; so are angles 5 and 4. Unlike corresponding angles, which lie on the same side of the transversal, alternate angles lie on different sides of the transversal.
Corresponding angles postulate
The corresponding angles postulate states that if two parallel lines are cut by a transversal, the corresponding angles are congruent .
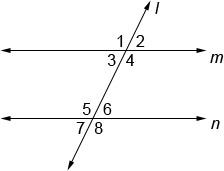
Parallel lines m and n are cut by transversal l above, forming four pairs of congruent, corresponding angles: ∠1 ≅ ∠5, ∠2 ≅ ∠6, ∠3 ≅ 7, and ∠4 ≅ ∠8.
This postulate tells us several things about the eight angles formed when a transversal intersects two lines:
- If one of the angles is a right angle, all of the angles are right angles.
- If one of the angles is acute, 4 of the angles are acute.
- If one of the angles is obtuse, 4 of the angles are obtuse.
- All of the angles can be classified as one of the following types of angles: corresponding, vertical, or adjacent.
The converse of the corresponding angles postulate is also true. If the corresponding angles of two lines cut by a transversal are congruent, then the lines are parallel.
Using corresponding angles and straight angles, find the measures of the angles formed by the intersection of parallel lines m and n cut by transversal l below.

- ∠2 ≅ ∠60° since they are corresponding angles, and m and n are parallel.
- ∠1 and ∠2 form a straight angle, so∠1=120°.
- ∠5 ≅ ∠120° since ∠1 and ∠5 are corresponding angles, and m and n are parallel.
- ∠7 and ∠5 form a straight angle, so∠7=60°.
- ∠3 ≅ ∠60° since ∠3 and ∠7 are corresponding angles, and m and n are parallel.
- ∠3 and ∠4 form a straight angle, so∠4=120°.
- ∠8 ≅ ∠120° since ∠4 and ∠8 are corresponding angles, and m and n are parallel.

Corresponding Angles
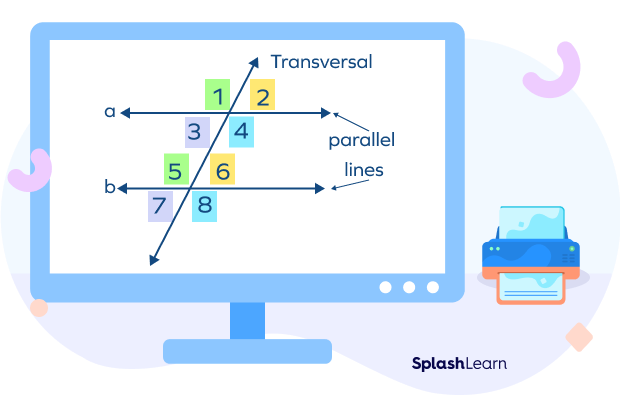
Corresponding angles are two angles that lie in similar relative positions on the same side of a transversal or at each intersection. They are usually formed when two parallel or non-parallel lines are cut by a transversal.
Remember that a transversal is a line that intersects two or more lines.
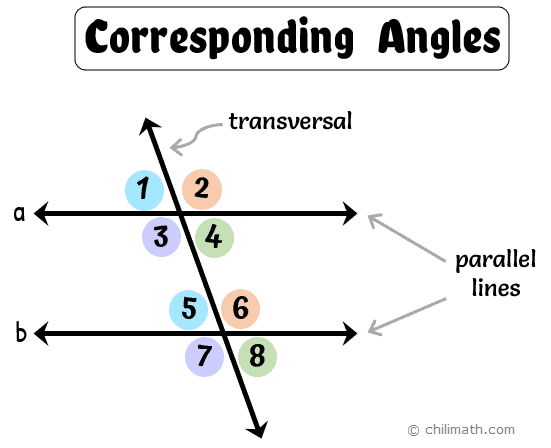
In our illustration above, parallel lines [latex]a[/latex] and [latex]b[/latex] are cut by a transversal which as a result, formed 4 corresponding angles. For example, [latex]\angle 2[/latex] and [latex]\angle 6[/latex] are corresponding angles. Why? Because both angles are located in matching corners or corresponding positions on the right-hand side of the transversal. In other words, each angle is located above the line and to the right of the transversal.
Here are our corresponding angles (must be in pairs) from the diagram and their location.
- [latex]\angle \textbf{1}[/latex] and [latex]\angle \textbf{5}[/latex] – above the line, left of the transversal
- [latex]\angle \textbf{3}[/latex] and [latex]\angle \textbf{7}[/latex] – below the line, left of the transversal
- [latex]\angle \textbf{2}[/latex] and [latex]\angle \textbf{6}[/latex] – above the line, right of the transversal
- [latex]\angle \textbf{4}[/latex] and [latex]\angle \textbf{8}[/latex] – below the line, right of the transversal
There are a few things to remember when dealing with corresponding angles.
Corresponding Angles Postulate
When two parallel lines are cut by a transversal, then the pairs of corresponding angles are congruent or have the same measure .
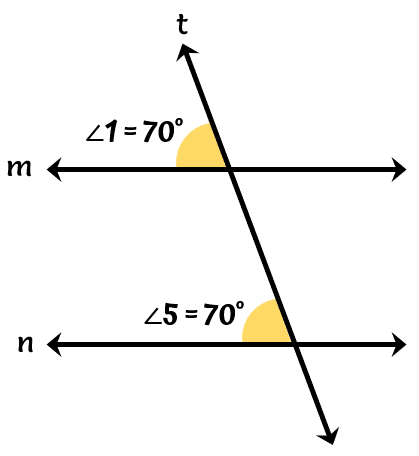
Take for example in our diagram above, since [latex]\angle 1[/latex] and [latex]\angle 5[/latex] are corresponding angles, they are congruent. This also means that if [latex]\angle 1[/latex] measures [latex]70^\circ [/latex] then [latex]\angle 5[/latex] also measures [latex]70^\circ [/latex]. Therefore, [latex]\angle 1 \cong \angle 5[/latex].
On the other hand, if the transversal intersects with two non-parallel lines , the corresponding angles formed are not congruent and do not have a specific relationship to each other.
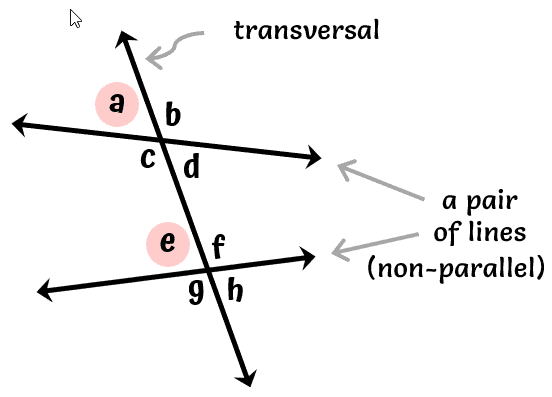
Hence, [latex]\angle a[/latex] and [latex]\angle e[/latex] are corresponding angles but are NOT congruent.
Example Problems Involving Corresponding Angles
Example 1: Identify the corresponding angles.
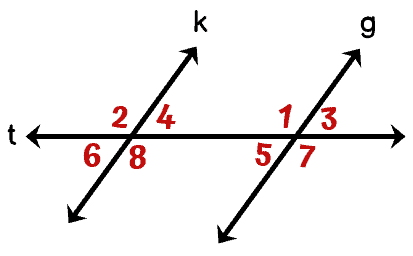
Here we have two parallel lines, lines [latex]k[/latex] and [latex]g[/latex], that are cut by the transversal, [latex]t[/latex]. Remember that corresponding angles are angles that are in similar positions on the same side of the transversal.
So the corresponding angles are:
- [latex]\angle 2[/latex] and [latex]\angle 1[/latex]
- [latex]\angle 4[/latex] and [latex]\angle 3[/latex]
- [latex]\angle 6[/latex] and [latex]\angle 5[/latex]
- [latex]\angle 8[/latex] and [latex]\angle 7[/latex]
Example 2: Name the pairs of corresponding angles and their location.
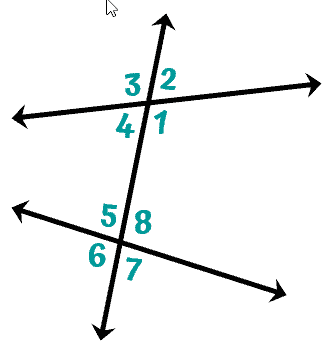
As you can see, the transversal cuts across two non-parallel lines forming 4 corresponding angles. Always remember that in this case, though the angles are located in corresponding positions relative to the two lines, they are not congruent.
The corresponding angles are:
- [latex]\angle 3[/latex] and [latex]\angle 5[/latex] – above the line, left of the transversal
- [latex]\angle 4[/latex] and [latex]\angle 6[/latex] – below the line, left of the transversal
- [latex]\angle 2[/latex] and [latex]\angle 8[/latex] – above the line, right of the transversal
- [latex]\angle 1[/latex] and [latex]\angle 7[/latex] – below the line, right of the transversal
Example 3: Find the measure of [latex]\angle 8[/latex].
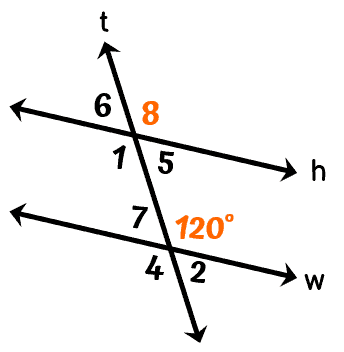
Since line [latex]h[/latex] and line [latex]w[/latex] are parallel lines, the measure of [latex]\angle 8[/latex] should be the same as its corresponding angle. Hence, the [latex]m\angle 8[/latex] is [latex]120^\circ[/latex].
You may also be interested in these related math lessons or tutorials:
Alternate Exterior Angles
Alternate Interior Angles
Complementary Angles
Supplementary Angles
Vertical Angles

Corresponding Angles – Definition, Theorem, Types, Examples
What are corresponding angles, types of corresponding angles, how to locate and identify corresponding angles, solved examples on corresponding angles, practice problems on corresponding angles, frequently asked questions about corresponding angles.
If two parallel lines or non-parallel lines are cut by a transversal, the angles at the in matching corners or corresponding corners on the same side of the transversal are called “corresponding angles.”
So, what do the corresponding angles look like? In each pair of corresponding angles, one angle is in the interior region of the two lines and one angle is in the exterior region.
Corresponding Angles: Definition
When two lines are crossed by a transversal, corresponding angles are pairs of angles that are in the same relative position in relation to a pair of intersecting lines.
Related Worksheets

The two cases that may arise while checking corresponding angles are as follows:
- Corresponding angles formed by parallel lines and transversals
When two or more parallel lines are cut by a transversal, then the corresponding angles are formed at the matching corners or at the same relative position at each intersection.
When the lines are parallel, each pair of corresponding angles are congruent .
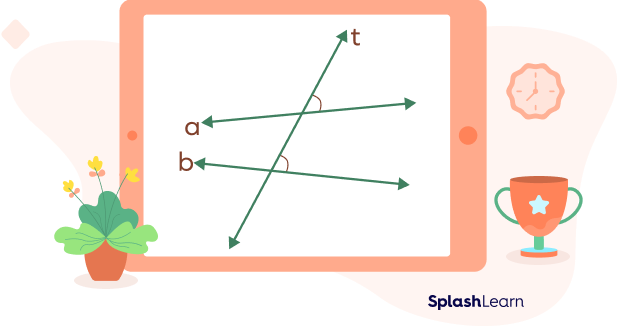
- Corresponding angles formed by non-parallel lines and transversals
In the case of non-parallel lines, the angles in previously stated positions will remain corresponding angles. However, they will not be equal in measure anymore. Two non-parallel lines form pairs of non-congruent corresponding angles.
Let’s understand how to identify which angles are corresponding angles when two parallel lines (or non-parallel lines) are cut by a transversal.
- They lie on the same side of the transversal.
- They lie at the matching corners.
- In each pair, one angle is in the interior region and the other is outside the two parallel (or non-parallel) lines.
- Corresponding angles form a F-shaped pattern.
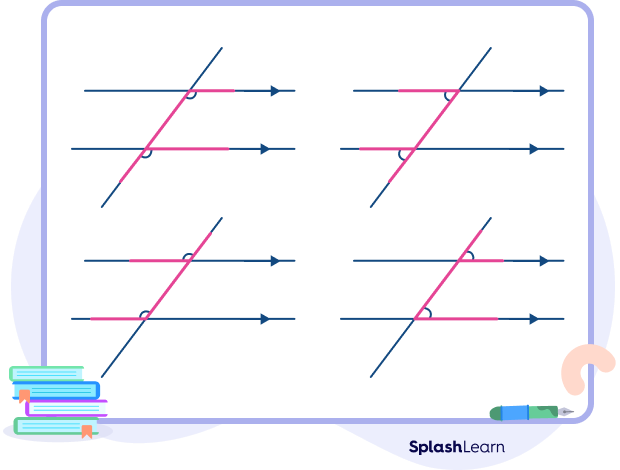
Corresponding Angles Theorem
The corresponding angle theorem states that when parallel lines are cut by a transversal, each pair of corresponding angles are congruent or equal.

Converse of Corresponding Angles Theorem
If the corresponding angles are congruent, the lines intersected by transversal are parallel.
Facts about Corresponding Angles
- If non-parallel lines are cut by a transversal, the corresponding angles are not congruent. There is no specific relationship between the corresponding angles.
- If parallel lines are cut by a transversal, the corresponding angles are congruent.
In this article, we learned about the corresponding angles formed by parallel lines and non-parallel lines with a transversal. Let’s solve a few examples and practice problems based on the concept of corresponding angles.
1. The measures of corresponding angles formed by two parallel lines and a transversal are (x + 20 ) ° and (3x + 9 ) ° . What is the value of x ?
Solution:
The corresponding angles formed by parallel lines and a transversal are always equal.
Thus, they are congruent.
x + 20 = 3x + 9
3x – x = 20 – 9
2. If EG and BD are two parallel lines, find the measure of the angle x.
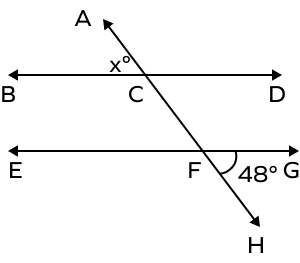
Solution: The angles ∠GFH and ∠EFC are vertically opposite angles.
Vertical angles are always congruent.
Thus, m∠CFE = m∠GFH = 48°
Now, the angles ∠EFC and ∠BCA are corresponding angles formed by parallel lines.
Thus, they will also be equal.
Thus, m∠EFC and m∠BCA = 48°.
3. Write all the pairs of corresponding angles.
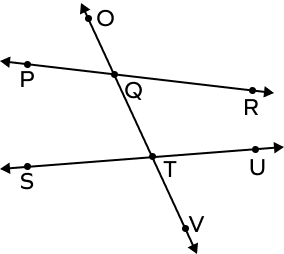
Solution:
Pairs of Corresponding Angles:
- ∠OQR and ∠QTU
- ∠RQT and ∠UTV
- ∠OQP and ∠QTS
- ∠PQT and ∠STV
Corresponding Angles - Definition, Theorem, Types, Examples
Attend this quiz & Test your knowledge.
If the corresponding angles are not congruent, then
Corresponding angles are equal, when ______ lines are cut by a transversal., what is the corresponding angle of ∠age.
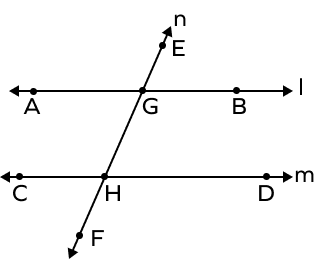
Are corresponding angles equal?
Corresponding angles formed when parallel lines are cut by a transversal are equal.
What are the relative positions of corresponding angles and a transversal?
Corresponding angles are formed on the same side of the transversal, at the matching corners.
Are corresponding angles supplementary?
No, corresponding angles need not be supplementary.
What is a transversal?
Transversal is the line intersecting two lines (parallel or non-parallel) at two distinct points.
RELATED POSTS
- Perimeter of a Semicircle – Definition, Formula, Examples, Facts
- Comparing Decimals – Definition, Solved Examples, Facts, FAQs
- Milliliters to Gallons Conversion
- Parallel and Perpendicular Lines – Definition With Examples
- Comparing and Ordering Numbers: Definition with Examples

Math & ELA | PreK To Grade 5
Kids see fun., you see real learning outcomes..
Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.
Parents, Try for Free Teachers, Use for Free
Pairs Of Angles
In these lessons, we look at how pairs of angles can relate to each other in several ways. Some examples are complementary angles , supplementary angles , vertical angles , alternate interior angles , alternate exterior angles , corresponding angles and adjacent angles .
Related Pages Angles Types Of Angles More Geometry Lessons
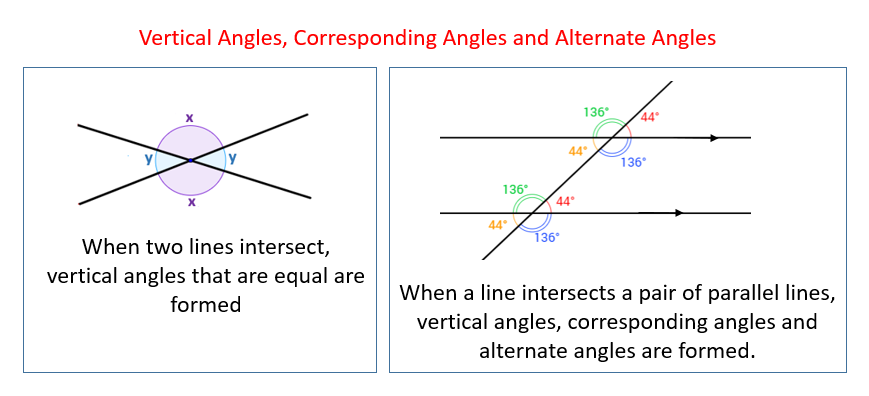
The following diagrams show how vertical angles, corresponding angles, and alternate angles are formed. Scroll down the page for more examples and solutions.
Complementary Angles
Two angles are called complementary angles if the sum of their degree measurements equals 90 degrees (right angle). One of the complementary angles is said to be the complement of the other.
The two angles do not need to be together or adjacent. They just need to add up to 90 degrees. If the two complementary angles are adjacent then they will form a right angle.
Supplementary Angles
Two angles are called supplementary angles if the sum of their degree measurements equals 180 degrees (straight line). One of the supplementary angles is said to be the supplement of the other.
The two angles do not need to be together or adjacent. They just need to add up to 180 degrees. If the two supplementary angles are adjacent then they will form a straight line.
Vertical Angles
Two pairs of angles are formed by two intersecting lines . Vertical angles are opposite angles in such an intersection. Vertical angles are equal to each other.
Very often math questions will require you to work out the values of angles given in diagrams by applying the relationships between the pairs of angles.
Example 1: Given the diagram below, determine the values of the angles x, y and z.
Solution: Step 1: x is a supplement of 65°. Therefore, x + 65° = 180° ⇒ x = 180° – 65° = 115°
Step 2: z and 115° are vertical angles. Therefore, z = 115°
Step 3: y and 65° are vertical angles. Therefore, y = 65°
Answer: x = 115°, y = 65° and z = 115°
How To Use Complementary, Supplementary, And Vertical Angle Pairs Property To Solve For X?
Alternate Interior Angles
When a line intersects a pair of parallel lines alternate interior angles are formed. Alternate interior angles are equal to each other.
One way to find the alternate interior angles is to draw a zigzag line on the diagram. In the above diagrams, d and e are alternate interior angles. Similarly, c and f are also alternate interior angles.
Example 1: Given the diagram below, determine the values of the angles b, c, d, e, f, g and h.
Solution: Step 1: b is a supplement of 60°. Therefore, b + 60° =180° ⇒ b = 180° – 60° = 120°
Step 2: b and c are vertical angles. Therefore, c = b = 120°
Step 3: d and 60° are vertical angles. Therefore, d = 60°
Step 4: d and e are alternate interior angles. Therefore, e = d = 60°
Step 5: f and e are supplementary angles. Therefore, f + 60° =180° ⇒ f = 180° – 60° = 120°
Step 6: g and f are vertical angles. Therefore, g = f = 120°
Step 7: h and e are vertical angles. Therefore, h = e = 60°
Answer: b = 120°, c = 120°, d = 60°, e = 60°, f = 120°, g = 120°and h = 60°
From the above example, you may notice that either an angle is 60° or it is 120°. Actually, all the small angles are 60° and all the big angles are 120°. In general, the diagram will be as shown below. The small and big pair of angles are supplementary (i.e. small + big = 180°). Therefore, given any one angle you would be able to work out the values of all the other angles.
How To Find Alternate Interior Angles?
If two parallel lines are intersected by a transversal then alternate interior angles are congruent.
Alternate Exterior Angles
One way to remember alternate exterior angles is that they are the vertical angles of the alternate interior angles . Alternate exterior anglesare equal to one another.
∠a and ∠h are alternate exterior angles and they are equal to one another.
∠b and ∠g are alternate exterior angles and they are equal to one another.
How To Find Alternate Exterior Angles? If two parallel lines are intersected by a transversal then alternate exterior angles are congruent.
Corresponding Angles
When a line intersects a pair of parallel lines corresponding angles are formed. Corresponding angles are equal to each other.
One way to find the corresponding angles is to draw a letter F on the diagram. The F can also be facing backwards.
In the above diagram, ∠d and ∠h are corresponding angles .
There many other corresponding pairs of angles in the diagram: ∠b and ∠f ; ∠c and ∠g ; ∠a and ∠e .
How To Find Congruent Corresponding Angles?
Adjacent Angles
When two angles are next to one another, they are called adjacent angles . Adjacent angles share a common side and a common vertex.
Example: ∠x and ∠y are adjacent angles.
How To Find Adjacent Angles?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
Corresponding Angles
When two lines are crossed by another line (called the Transversal ):
The angles in matching corners are called Corresponding Angles .
In this example a and e are corresponding angles
Also: • b and f are corresponding angles • c and g are corresponding angles • d and h are corresponding angles
Parallel Lines
When the two lines being crossed are Parallel Lines the Corresponding Angles are equal .
(Click on "Corresponding Angles" to have them highlighted for you.)
Free Printable Math Worksheets for Geometry
Created with infinite geometry, stop searching. create the worksheets you need with infinite geometry..
- Fast and easy to use
- Multiple-choice & free-response
- Never runs out of questions
- Multiple-version printing
Free 14-Day Trial
- Review of equations
- Simplifying square roots
- Adding and subtracting square roots
- Multiplying square roots
- Dividing square roots
- Line segments and their measures inches
- Line segments and their measures cm
- Segment Addition Postulate
- Angles and their measures
- Classifying angles
- Naming angles
- The Angle Addition Postulate
- Angle pair relationships
- Understanding geometric diagrams and notation
- Parallel lines and transversals
- Proving lines parallel
- Points in the coordinate plane
- The Midpoint Formula
- The Distance Formula
- Parallel lines in the coordinate plane
- Classifying triangles
- Triangle angle sum
- The Exterior Angle Theorem
- Triangles and congruence
- SSS and SAS congruence
- ASA and AAS congruence
- SSS, SAS, ASA, and AAS congruences combined
- Right triangle congruence
- Isosceles and equilateral triangles
- Midsegment of a triangle
- Angle bisectors
- The Triangle Inequality Theorem
- Inequalities in one triangle
- Classifying quadrilaterals
- Angles in quadrilaterals
- Properties of parallelograms
- Properties of trapezoids
- Properties of rhombuses
- Properties of kites
- Areas of triangles and quadrilaterals
- Introduction to polygons
- Polygons and angles
- Areas of regular polygons
- Solving proportions
- Similar polygons
- Using similar polygons
- Similar triangles
- Similar right triangles
- Proportional parts in triangles and parallel lines
- The Pythagorean Theorem and its Converse
- Multi-step Pythagorean Theorem problems
- Special right triangles
- Multi-step special right triangle problems
- Trig. ratios
- Inverse trig. ratios
- Solving right triangles
- Multi-step trig. problems
- Rhombuses and kites with right triangles
- Trigonometry and area
- Identifying solid figures
- Volume of prisms and cylinders
- Surface area of prisms and cylinders
- Volume of pyramids and cones
- Surface area of pyramids and cones
- More on nets of solids
- Similar solids
- Arcs and central angles
- Arcs and chords
- Circumference and area
- Inscribed angles
- Tangents to circles
- Secant angles
- Secant-tangent and tangent-tangent angles
- Segment measures
- Equations of circles
- Translations
- Reflections
- All transformations combined
- Sample spaces and The Counting Principle
- Independent and dependent events
- Mutualy exclusive events
- Permutations
- Combinations
- Permutations vs combinations
- Probability using permutations and combinations
- Line segments
- Perpendicular segments
- Medians of triangles
- Altitudes of triangles

In order to continue enjoying our site, we ask that you confirm your identity as a human. Thank you very much for your cooperation.
Angle Relationships (Types of Angles)
Types of angles.
In geometry, there are many types of angles such as congruent, adjacent, vertical, corresponding, alternating, exterior, and interior angles. All angles have relationships to other angles and those angle relationships are what we will cover here.
Angle relationships
Beyond measuring the degrees or radians, you can also compare angles and consider their relationships to other angles. We talk of angle relationships because we are comparing position, measurement, and congruence between two or more angles.

For example, when two lines or line segments intersect, they form two pairs of vertical angles. When two parallel lines are intersected by a transversal, complex angle relationships form, such as alternating interior angles, corresponding angles, and so on.
Being able to spot angle relationships, and confidently find congruent angles when lines intersect, will make you a better, geometry student. You will solve complex problems faster when you are thoroughly familiar with all the types of angle relationships.
Congruent angles
Any two angles, no matter their orientation, that have equal measures (in radians or degrees) are congruent . They show the same "openness" between the two rays, line segments or lines that form them. So these two 35° angles are congruent, even if they are not identically presented, and are formed with different constructions:

Adjacent angles
When two lines cross each other, they form four angles. Any two angles sharing a ray, line segment or line are adjacent . In the following drawing, Line JC intersects Line OK , creating four adjacent pairs and intersecting at Point Y . Can you find them all?

Did you find ∠JYO adjacent to ∠OYC ?
How about ∠OYC adjacent to ∠KYC ?
You saw ∠KYC adjacent to ∠KYJ , right?
And you found ∠KYJ adjacent to ∠JYO , surely!
Vertical angles
In our same drawing above, angles that skip an angle, that is, angles that are not touching each other except at their vertex, are vertical angles . Here the word "vertical" means "relating to a vertex," not "up and down." Vertical angles are opposite angles; they share only their vertex point.

Two intersecting lines create two pairs of vertical angles. See if you can spot them in our drawing.
Did you find ∠JYO and ∠KYC made a pair? They touch only at Point Y
Did you find ∠KYJ and ∠OYC made the other pair? They also touch only at Point Y
You may wonder why adjacent angles are not also vertical angles, since they share the vertex, too. Adjacent angles share more than the vertex; they share a common side to an angle.
Corresponding angles
Anytime a transversal crosses two other lines, we get corresponding angles . The more restrictive our intersecting lines get, the more restrictive are their angle relationships. When a line crosses two parallel lines (a transversal), a whole new level of angle relationships opens up:

We can adroitly pull from this figure angles that look like each other. Angles that have the same position relative to one another in the two sets of four angles (four at the top, Line AR ; four at the bottom, Line TO ) are corresponding angles. When the corresponding angles are on parallel lines, they are congruent.
Our transversal and parallel lines create four pairs of corresponding angles. Can you name them all?
Did you find ∠AYD corresponding to ∠TLY ?
How about ∠DYR corresponding to ∠YLO ?
You found ∠RYL corresponding to ∠OLI , right?
And you did not overlook ∠AYL corresponding to ∠TLI , did you?
In all cases, since our Line AR and TO are parallel, their corresponding angles are congruent.
Exterior angles
Those same parallel lines and their transversal create exterior angles. An exterior angle among line constructions (not polygons) is one that lies outside the parallel lines. You can see two types of exterior angle relationships:
Consecutive exterior angles
When the exterior angles are on the same side of the transversal, they are consecutive exterior angles, and they are supplementary (adding to 180° ). In our figure above, ∠AYD and ∠TLI are consecutive exterior angles. The only other pair of consecutive exterior angles is ∠DYR and ∠OLI.

Alternate exterior angles
Alternate exterior angles are similar to vertex angles, in that they are opposite angles (on either side of the transversal). Alternate exterior angles are on opposite sides of the transversal (that's the alternate part) and outside the parallel lines (that's the exterior part). Can you find the two pairs of alternate exterior angles in our drawing?
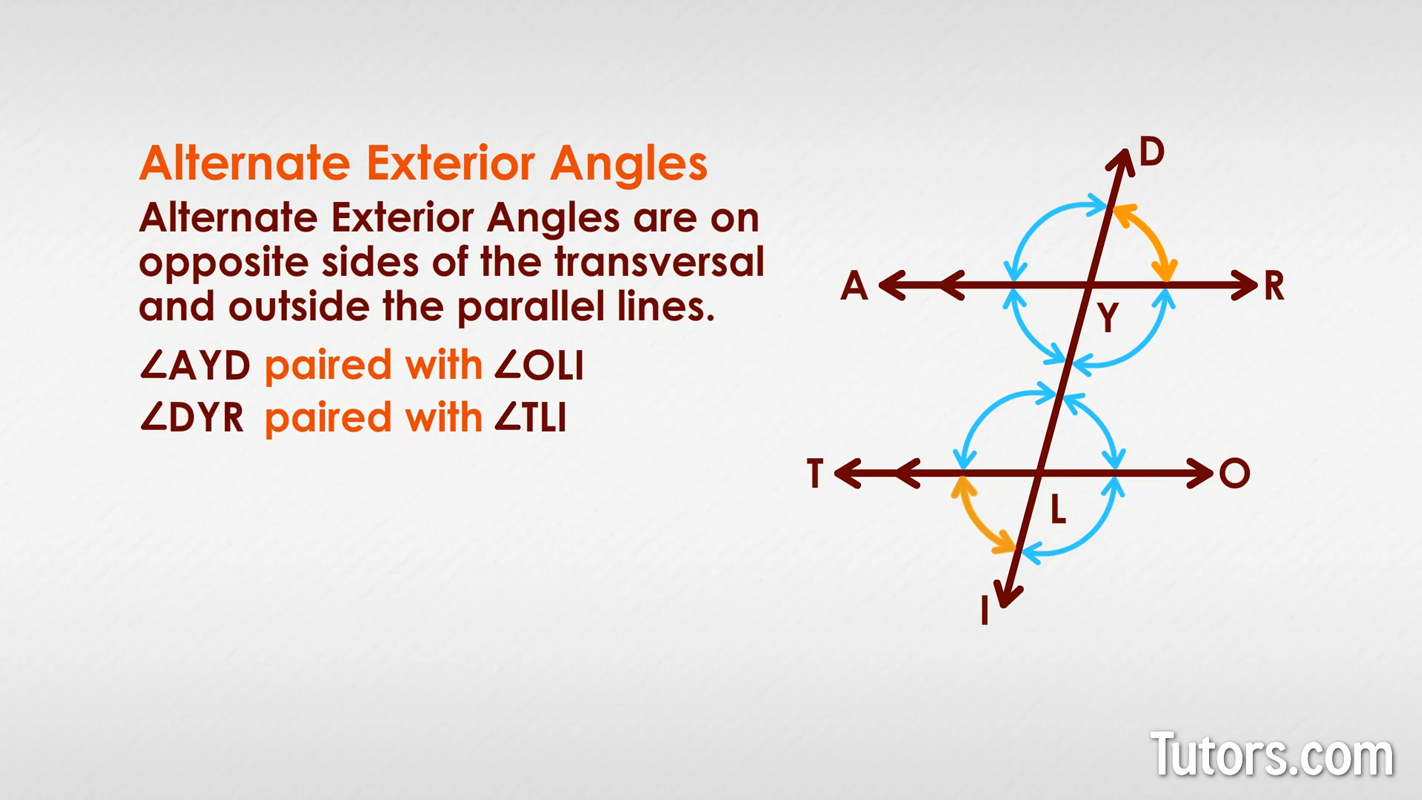
You wrote down ∠AYD and ∠OLI , and then you wrote ∠DYR paired with ∠TLI , no doubt!
Congruent alternate exterior angles are used to prove that lines are parallel, using (fittingly) the Alternate Exterior Angles Theorem.
Interior angles
Angles between the bounds of the two parallel lines are interior angles , again created by the transversal. Just as with exterior angles, we can have consecutive interior angles and alternate interior angles.
Consecutive Interior Angles
Interior angles on the same side of the transversal are consecutive interior angles . In our figure, can you find the two pairs? Did you find ∠RYL pairing off with ∠YLO ? Did you see that ∠AYL paired up with ∠TLY ?
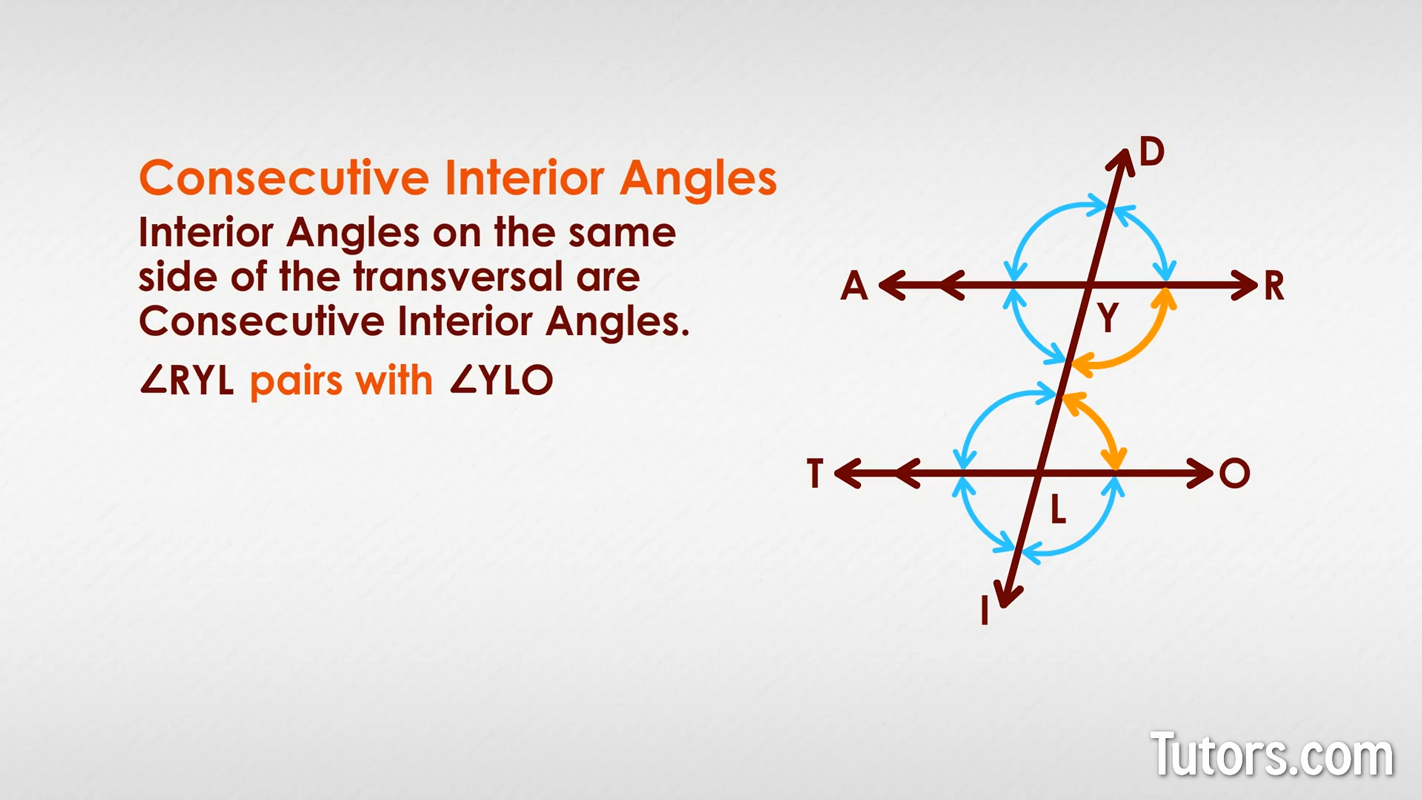
In parallel lines, consecutive interior angles are supplementary.
Alternate interior angles
When the interior angles are on opposite sides of the transversal, they are alternate interior angles . They lend themselves to the Alternate Interior Angles Theorem, which states that congruent alternate interior angles prove parallel lines (much as the Alternate Exterior Angles Theorem did).
In our figure, ∠ALY is the alternate interior angle for ∠YLO , making them congruent. And, of course, ∠RYL pairs off as the alternate interior angle of ∠TLY .
Angle relationships examples
You can use your newfound knowledge of angle relationships to solve algebraic challenges about geometric figures. When viewing any new figure, go through your list and determine three things:
Relative positions of the two questioned angles
Whether the angles are outside the parallel lines (exterior) or inside the parallel lines (interior)
Whether the two angles under investigation are on the same side of the transversal (consecutive) or opposite sides of the transversal (alternate)
Once you understand the relationship between the two angles, you can assume some basic facts, such as their congruence or that they may be supplementary.
You can use that awareness to solve seemingly difficult algebraic problems like this:
Draw parallel lines MJ and TE and the transversal AS with intersecting Point C on Line MJ and intersecting Point I on Line TE , spelling in a circular way MAJESTIC. Let ∠MCA = 123° .
Given the figure, find the value of x if ∠ MCA = 4x + 3° while ∠EIS = 5x − 27° .
You see right away that these two angles, ∠MCA and ∠EIS , are exterior angles on opposite sides of the transversal. So they are alternate exterior angles, making them congruent and allowing you to set up a simple algebraic equation:
Next, we subtract 4 x from both sides:
Next, we add 27° to both sides:
To find our angles, substitute 30° for x :
Though ∠EIS is supposed to be congruent, you can still check it:
Let's try a second exercise, using the same figure. If you can solve this, you will have accomplished some MAJESTIC mathematics!
What can you tell us about ∠JCI and ∠TIS ?
What if we told you ∠JCI = 2y − 7° while ∠TIS = y − 8° ?
Can you solve for y ?
Neither angle is on the same side of the transversal, nor are they both outside the parallel lines. They are not both inside the parallel lines, either! They seem to have no relationship at all!
And yet, by deduction, you can see a relationship:
∠JCI is the consecutive interior angle partner of ∠EIC
∠EIC is the vertical angle partner of ∠TIS
This means our two problematic angles are actually supplementary, which is a great hint. Together, their two equations must add to 180° :
Now, simplify:
Need 15° to both sides:
Working back through the problem, you will find that ∠JCI = 123° and ∠TIS = 57° . Success! Practice for yourself, by constructing parallel lines with transversals and identifying all the angle relationships they create.
Remember, too, the relationships still hold when the lines cut by the transversal are not parallel; you just cannot use Theorems to make assumptions about the angles.

IMAGES
VIDEO
COMMENTS
Kuta Software - Infinite Geometry Name_____ Parallel Lines and Transversals Date_____ Period____ Identify each pair of angles as corresponding, alternate interior, alternate exterior, or consecutive interior. 1) y x 2) y x 3) y x 4) y x 5) y x 6) y x 7) y x 8) y x-1-©i L2c0 j1e1 2 wKcuXtwaN NSmoFfft DwxaTr1eS OLwLXCZ. 4 b GAKlzl x 7rHi1gVhntis ...
Geometry chapter 5 vocab. 12 terms. SIENNA_SCHURING. Preview. Unit 6: Polygons and Quadrilaterals. 11 terms. Talia_Bisbe. Preview. Geometry Terms August. ... Identify each pair of angles as corresponding, alternate interior, alternate exterior, consecutive interior, vertical, or adjacent. 113 degrees. Find the measure of the angle indicated.
Example 2: find pairs of corresponding angles. \overleftarrow {\,S}\overrightarrow {Y\,} S Y and \overleftarrow {\,T}\overrightarrow {Z\,} T Z are parallel lines. Name all pairs of corresponding angles. Identify two parallel lines that are intersected by a transversal. The two parallel lines are SY S Y and TZ. TZ. Line UX U X is the transversal ...
Angle a Given that the two lines are parallel , find the value of x and all other angles. 60 1. Angle b = _____ 2. Angle a = _____ 3. Angle d = _____ 4. Angle e = _____ 5. Angle f = _____ 6. Angle g = _____ 7. Angle h = _____ and b Angle c and f Angle a and h Angle b and f Angle e and h Angle d and e
Angle Pair Relationships Date_____ Period____ Name the relationship: complementary, linear pair, vertical, or adjacent. 1) a b linear pair 2) a b adjacent 3) a b adjacent 4) a b complementary 5) a b vertical 6) a b adjacent 7) a b linear pair 8) a b vertical Find the measure of angle b. 9) b 50° 130° 10) 43° b 43° 11) 209° 96° b 55° 12 ...
Refer to the figure below. The corresponding angles are the angles that lie on the same side of the transversal in matching corners. In other words, they occupy the same relative position in the figure. In a pair of corresponding angles, one is an exterior angle and one is an interior angle. In the figure, transversal l intersects lines m and n ...
Corresponding angles are two angles that lie in similar relative positionson the same side of a transversal or at each intersection. They are usually formed when two parallel or non-parallel lines are cut by a transversal. Remember that a transversalis a line that intersects two or more lines. In our illustration above, parallel lines [latex]a ...
Corrective Assignment 3.1 Identify each pair of angles as corresponding, alternate exterior, alternate interior or same-side interior angles. ... Corresponding angles are on the same side of the transversal 15) Two skew lines are coplanar 17) Two planes that do not intersect are parallel.
In each pair, one angle is in the interior region and the other is outside the two parallel (or non-parallel) lines. Corresponding angles form a F-shaped pattern. Corresponding Angles Theorem. The corresponding angle theorem states that when parallel lines are cut by a transversal, each pair of corresponding angles are congruent or equal.
Corresponding Angles. When a line intersects a pair of parallel lines corresponding angles are formed. Corresponding angles are equal to each other. One way to find the corresponding angles is to draw a letter F on the diagram. The F can also be facing backwards. In the above diagram, ∠d and ∠h are corresponding angles.
Angles between two lines and on opposite sides of a transversal. Angles that lie outside a pair of lines and on opposite sides of a transversal. Angles that are on the same side of the transversal and inside the two lines. If two parallel lines are cut by a transversal, then the alternate interior angles are congruent.
Corresponding Angles. Corresponding Angles. When two lines are crossed by another line (called the Transversal ): The angles in matching corners are called Corresponding Angles. In this example a and e are corresponding angles. Also: • b and f are corresponding angles • c and g are corresponding angles • d and h are corresponding angles.
1. Line(s) parallel to CD and containing point A. 2. Line(s) skew to CD and containing point A. suur suu r 3. Line(s) perpendicular to CD and containing point A. 4. Plane(s) parallel to EFG. * If there is a line and a point not on that line, there exists exactly one line through that point, parallel to the given line.
Two angles are said to be Supplementary Angles if their sum is 180 degrees. The angles A and B shown in the figure are complementary since their angle sum is 180°. + B = 180°. A. Vertical Angles are the angles opposite each other when two lines are intersect. The two vertical angles are congruent. The angles A and B shown in the figure are ...
Corresponding angles are two angles that are in the "same place" with respect to the transversal but on different lines. Imagine sliding the four angles formed with line l down to line m. The angles which match up are corresponding. Corresponding Angles Postulate: If two parallel lines are cut by a transversal, then the corresponding angles are ...
Angles. Triangles. Medians of triangles. Altitudes of triangles. Angle bisectors. Circles. Free Geometry worksheets created with Infinite Geometry. Printable in convenient PDF format.
Our expert help has broken down your problem into an easy-to-learn solution you can count on. Question: Identify each pair of angles as corresponding, alternate interior, alternate exterior, same-side interior, vertical, or adjacent. 1) 2) 3) 5) Here's the best way to solve it.
Geometry Assignment Name Date ID: I Period Identify each pair of angles as corresponding, alternate interior, or alternate exterior. c orresponding altemate interior c orresp onding Find the measure of each angle indicated. 830 1270 1270 alternate interior c orresp onding a Iternate exterior 840 10) 630 630
Step 1: Identify the corresponding angles. Corresponding angles will be on the same side of the transversal and in the same position relative to one of the parallel lines. Step 2: Identify the ...
For example, when two lines or line segments intersect, they form two pairs of vertical angles. When two parallel lines are intersected by a transversal, complex angle relationships form, such as alternating interior angles, corresponding angles, and so on. Being able to spot angle relationships, and confidently find congruent angles when lines ...
Learn how to identify and use corresponding angles. Click Create Assignment to assign this modality to your LMS. We have a new and improved read on this topic.
Geometry Assignment ... ©M L2R0^2a0[ [KNudtna` JSxoGfLtjwtaarzeY JLQL`Cc.V R NAHl_ll hr_iZg_hxtDsb trlebsseDrnvIepdU. Identify each pair of angles as corresponding, alternate interior, same-side interior, or vertical. 1) y x 2) y x 3) y x 4) y x 5) y x 6) y x Find the measure of each angle indicated. 7) ? 127° ...
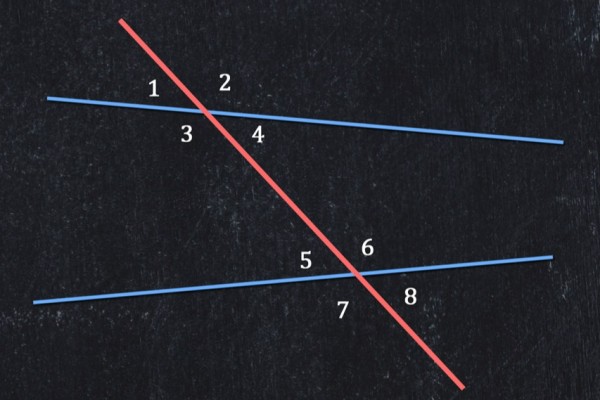
When two lines are crossed by another line, the angles in matching corners are corresponding angles. Therefore, observing the figure we can conclude that pairs. ∠ 2 and ∠ 6 \angle 2 \text{ and } \angle 6 ∠2 and ∠6. ∠ 1 and ∠ 5 \angle 1 \text{ and } \angle 5 ∠1 and ∠5. ∠ 4 and ∠ 8 \angle 4 \text{ and } \angle 8 ∠4 and ∠8. and