Module 11: Chi-Square Tests

Test of Homogeneity
Learning outcomes.
- Conduct a chi-square test of homogeneity. Interpret the conclusion in context.
We have learned the details for two chi-square tests, the goodness-of-fit test, and the test of independence. Now we focus on the third and last chi-square test that we will learn, the test for homogeneity . This test determines if two or more populations (or subgroups of a population) have the same distribution of a single categorical variable.
The test of homogeneity expands the test for a difference in two population proportions, which is the two-proportion Z-test we learned in Inference for Two Proportions . We use the two-proportion Z-test when the response variable has only two outcome categories and we are comparing two populations (or two subgroups.) We use the test of homogeneity if the response variable has two or more categories and we wish to compare two or more populations (or subgroups.)
We can answer the following research questions with a chi-square test of homogeneity:
- Does the use of steroids in collegiate athletics differ across the three NCAA divisions?
- Was the distribution of political views (liberal, moderate, conservative) different for last three presidential elections in the United States?
The null hypothesis states that the distribution of the categorical variable is the same for the populations (or subgroups). In other words, the proportion with a given response is the same in all of the populations, and this is true for all response categories. The alternative hypothesis says that the distributions differ.
Note: Homogeneous means the same in structure or composition. This test gets its name from the null hypothesis, where we claim that the distribution of the responses are the same (homogeneous) across groups.
To test our hypotheses, we select a random sample from each population and gather data on one categorical variable. As with all chi-square tests, the expected counts reflect the null hypothesis. We must determine what we expect to see in each sample if the distributions are identical. As before, the chi-square test statistic measures the amount that the observed counts in the samples deviate from the expected counts.
Steroid Use in Collegiate Sports
In 2006, the NCAA published a report called “Substance Use: NCAA Study of Substance Use of College Student-Athletes.” We use data from this report to investigate the following question: Does steroid use by student athletes differ for the three NCAA divisions?
The data comes from a random selection of teams in each NCAA division. The sampling plan was somewhat complex, but we can view the data as though it came from a random sample of athletes in each division. The surveys are anonymous to encourage truthful responses.
To see the NCAA report on substance use, click here .
Step 1: State the hypotheses.
In the test of homogeneity, the null hypothesis says that the distribution of a categorical response variable is the same in each population. In this example, the categorical response variable is steroid use (yes or no). The populations are the three NCAA divisions.
- H 0 : The proportion of athletes using steroids is the same in each of the three NCAA divisions.
- H a : The proportion of athletes using steroids is not same in each of the three NCAA divisions.
Note: These hypotheses imply that the proportion of athletes not using steroids is also the same in each of the three NCAA divisions, so we don’t need to state this explicitly. For example, if 2% of the athletes in each division are using steroids, then 98% are not.
Here is an alternative way we could state the hypotheses for a test of homogeneity.
- H 0 : For each of the three NCAA divisions, the distribution of “yes” and “no” responses to the question about steroid use is the same.
- H a : The distribution of responses is not the same.
Step 2: Collect and analyze the data.
We summarized the data from these three samples in a two-way table.
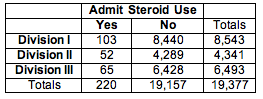
We use percentages to compare the distributions of yes and no responses in the three samples. This step is similar to our data analysis for the test of independence.
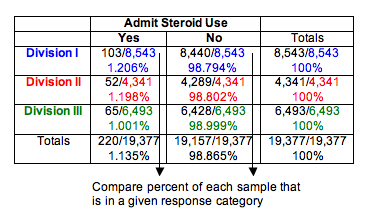
We can see that Division I and Division II schools have essentially the same percentage of athletes who admit steroid use (about 1.2%). Not surprisingly, the least competitive division, Division III, has a slightly lower percentage (about 1.0%). Do these results suggest that the proportion of athletes using steroids is the same for the three divisions? Or is the difference seen in the sample of Division III schools large enough to suggest differences in the divisions? After all, the sample sizes are very large. We know that for large samples, a small difference can be statistically significant. Of course, we have to conduct the test of homogeneity to find out.
Note: We decided not to use ribbon charts for visual comparison of the three distributions because the percentage admitting steroid use is too small in each sample to be visible.
Step 3: Assess the evidence.
We need to determine the expected values and the chi-square test statistic so that we can find the P-value.
Calculating Expected Values for a Test of Homogeneity
Expected counts always describe what we expect to see in a sample if the null hypothesis is true. In this situation, we expect the percentage using steroids to be the same for each division. What percentage do we use? We find the percentage using steroids in the combined samples. This calculation is the same as we did when finding expected counts for a test of independence, though the logic of the calculation is subtly different.
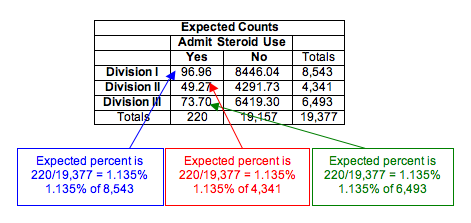
Here are the calculations for the response “yes”:
- Percentage using steroids in combined samples: 220/19,377 = 0.01135 = 1.135%
Expected count of steroid users for Division I is 1.135% of Division I sample:
- 0.01135(8,543) = 96.96
Expected count of steroid users for Division II is 1.135% of Division II sample:
- 0.01135(4,341) = 49.27
Expected count of steroid users for Division III is 1.135% of Division III sample:
- 0.01135(6,493) = 73.70
Checking Conditions
The conditions for use of the chi-square distribution are the same as we learned previously:
- A sample is randomly selected from each population.
- All of the expected counts are 5 or greater.
Since this data meets the conditions, we can proceed with calculating the χ 2 test statistic.
Calculating the Chi-Square Test Statistic
There are no changes in the way we calculate the chi-square test statistic.
[latex]X^2 = \Sigma \frac {(observed-expected)^2} {expected}[/latex]
We use technology to calculate the chi-square value. For this example, we show the calculation. There are six terms, one for each cell in the 3 × 2 table. (We ignore the totals, as always.)

Finding Degrees of Freedom and the P-Value
For chi-square tests based on two-way tables (both the test of independence and the test of homogeneity), the degrees of freedom are ( r − 1)( c − 1), where r is the number of rows and c is the number of columns in the two-way table (not counting row and column totals). In this case, the degrees of freedom are (3 − 1)(2 − 1) = 2.
We use the chi-square distribution with df = 2 to find the P-value. The P-value is large (0.4561), so we fail to reject the null hypothesis.
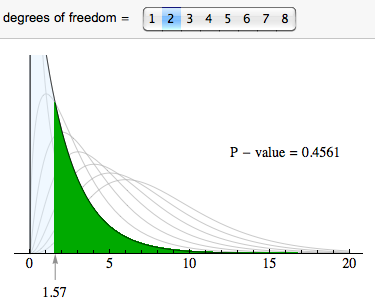
Step 4: Conclusion.
The data does not provide strong enough evidence to conclude that steroid use differs in the three NCAA divisions (P-value = 0.4561).
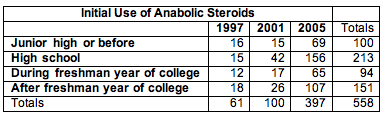
First Use of Anabolic Steroids by NCAA Athletes
The NCAA survey includes this question: “When, if ever, did you start using anabolic steroids?” The response options are: have never used, before junior high, junior high, high school, freshman year of college, after freshman year of college. We focused on those who admitted use of steroids and compared the distribution of their responses for the years 1997, 2001, and 2005. (These are the years that the NCAA conducted the survey. Counts are estimates from reported percentages and sample size.) Recall that the NCAA uses random sampling in its sampling design.
Use this simulation to answer the questions below.
We now know the details for the chi-square test for homogeneity. We conclude with two activities that will give you practice recognizing when to use this test.
Gender and Politics
Consider these two situations:
- A: Liberal, moderate, or conservative: Are there differences in political views of men and women in the United States? We survey a random sample of 100 U.S. men and 100 U.S. women.
- B: Do you plan to vote in the next presidential election? We ask a random sample of 100 U.S. men and 100 U.S. women. We look for differences in the proportion of men and women planning to vote.
Steroid Use for Male Athletes in NCAA Sports
We plan to compare steroid use for male athletes in NCAA baseball, basketball, and football. We design two different sampling plans.
- A: Survey distinct random samples of NCAA athletes from each sport: 500 baseball players, 400 basketball players, 900 football players.
- B. Survey a random sample of 1,800 NCAA male athletes and categorize players by sport and admitted steroid use. Responses are anonymous.
Let’s Summarize
In “Chi-Square Tests for Two-Way Tables,” we discussed two different hypothesis tests using the chi-square test statistic:
- Test of independence for a two-way table
- Test of homogeneity for a two-way table
Test of Independence for a Two-Way Table
- In the test of independence, we consider one population and two categorical variables.
- In Probability and Probability Distribution , we learned that two events are independent if P ( A | B ) = P ( A ), but we did not pay attention to variability in the sample. With the chi-square test of independence, we have a method for deciding whether our observed P ( A | B ) is “too far” from our observed P ( A ) to infer independence in the population.
- The null hypothesis says the two variables are independent (or not associated). The alternative hypothesis says the two variables are dependent (or associated).
- To test our hypotheses, we select a single random sample and gather data for two different categorical variables.
- Example: Do men and women differ in their perception of their weight? Select a random sample of adults. Ask them two questions: (1) Are you male or female? (2) Do you feel that you are overweight, underweight, or about right in weight?
Test of Homogeneity for a Two-Way Table
- In the test of homogeneity, we consider two or more populations (or two or more subgroups of a population) and a single categorical variable.
- The test of homogeneity expands on the test for a difference in two population proportions that we learned in Inference for Two Proportions by comparing the distribution of the categorical variable across multiple groups or populations.
- The null hypothesis says that the distribution of proportions for all categories is the same in each group or population. The alternative hypothesis says that the distributions differ.
- To test our hypotheses, we select a random sample from each population or subgroup independently. We gather data for one categorical variable.
- Example: Is the rate of steroid use different for different men’s collegiate sports (baseball, basketball, football, tennis, track/field)? Randomly select a sample of athletes from each sport and ask them anonymously if they use steroids.
The difference between these two tests is subtle. They differ primarily in study design. In the test of independence, we select individuals at random from a population and record data for two categorical variables. The null hypothesis says that the variables are independent. In the test of homogeneity, we select random samples from each subgroup or population separately and collect data on a single categorical variable. The null hypothesis says that the distribution of the categorical variable is the same for each subgroup or population.
Both tests use the same chi-square test statistic.
Chi-Square Test Statistic and Distribution
For all chi-square tests, the chi-square test statistic χ 2 is the same. It measures how far the observed data are from the null hypothesis by comparing observed counts and expected counts. Expected counts are the counts we expect to see if the null hypothesis is true.
The chi-square model is a family of curves that depend on degrees of freedom. For a two-way table, the degrees of freedom equals ( r − 1)( c − 1). All chi-square curves are skewed to the right with a mean equal to the degrees of freedom.
A chi-square model is a good fit for the distribution of the chi-square test statistic only if the following conditions are met:
- The sample is randomly selected.
- All expected counts are 5 or greater.
If these conditions are met, we use the chi-square distribution to find the P-value. We use the same logic that we have used in all hypothesis tests to draw a conclusion based on the P-value. If the P-value is at least as small as the significance level, we reject the null hypothesis and accept the alternative hypothesis. The P-value is the likelihood that results from random samples have a χ 2 value equal to or greater than that calculated from the data if the null hypothesis is true.
- Concepts in Statistics. Provided by : Open Learning Initiative. Located at : http://oli.cmu.edu . License : CC BY: Attribution
Concepts in Statistics Copyright © 2023 by CUNY School of Professional Studies is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License , except where otherwise noted.
Share This Book
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
- Null and Alternative Hypotheses | Definitions & Examples
Null & Alternative Hypotheses | Definitions, Templates & Examples
Published on May 6, 2022 by Shaun Turney . Revised on June 22, 2023.
The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test :
- Null hypothesis ( H 0 ): There’s no effect in the population .
- Alternative hypothesis ( H a or H 1 ) : There’s an effect in the population.
Table of contents
Answering your research question with hypotheses, what is a null hypothesis, what is an alternative hypothesis, similarities and differences between null and alternative hypotheses, how to write null and alternative hypotheses, other interesting articles, frequently asked questions.
The null and alternative hypotheses offer competing answers to your research question . When the research question asks “Does the independent variable affect the dependent variable?”:
- The null hypothesis ( H 0 ) answers “No, there’s no effect in the population.”
- The alternative hypothesis ( H a ) answers “Yes, there is an effect in the population.”
The null and alternative are always claims about the population. That’s because the goal of hypothesis testing is to make inferences about a population based on a sample . Often, we infer whether there’s an effect in the population by looking at differences between groups or relationships between variables in the sample. It’s critical for your research to write strong hypotheses .
You can use a statistical test to decide whether the evidence favors the null or alternative hypothesis. Each type of statistical test comes with a specific way of phrasing the null and alternative hypothesis. However, the hypotheses can also be phrased in a general way that applies to any test.
Here's why students love Scribbr's proofreading services
Discover proofreading & editing
The null hypothesis is the claim that there’s no effect in the population.
If the sample provides enough evidence against the claim that there’s no effect in the population ( p ≤ α), then we can reject the null hypothesis . Otherwise, we fail to reject the null hypothesis.
Although “fail to reject” may sound awkward, it’s the only wording that statisticians accept . Be careful not to say you “prove” or “accept” the null hypothesis.
Null hypotheses often include phrases such as “no effect,” “no difference,” or “no relationship.” When written in mathematical terms, they always include an equality (usually =, but sometimes ≥ or ≤).
You can never know with complete certainty whether there is an effect in the population. Some percentage of the time, your inference about the population will be incorrect. When you incorrectly reject the null hypothesis, it’s called a type I error . When you incorrectly fail to reject it, it’s a type II error.
Examples of null hypotheses
The table below gives examples of research questions and null hypotheses. There’s always more than one way to answer a research question, but these null hypotheses can help you get started.
| ( ) | ||
| Does tooth flossing affect the number of cavities? | Tooth flossing has on the number of cavities. | test: The mean number of cavities per person does not differ between the flossing group (µ ) and the non-flossing group (µ ) in the population; µ = µ . |
| Does the amount of text highlighted in the textbook affect exam scores? | The amount of text highlighted in the textbook has on exam scores. | : There is no relationship between the amount of text highlighted and exam scores in the population; β = 0. |
| Does daily meditation decrease the incidence of depression? | Daily meditation the incidence of depression.* | test: The proportion of people with depression in the daily-meditation group ( ) is greater than or equal to the no-meditation group ( ) in the population; ≥ . |
*Note that some researchers prefer to always write the null hypothesis in terms of “no effect” and “=”. It would be fine to say that daily meditation has no effect on the incidence of depression and p 1 = p 2 .
The alternative hypothesis ( H a ) is the other answer to your research question . It claims that there’s an effect in the population.
Often, your alternative hypothesis is the same as your research hypothesis. In other words, it’s the claim that you expect or hope will be true.
The alternative hypothesis is the complement to the null hypothesis. Null and alternative hypotheses are exhaustive, meaning that together they cover every possible outcome. They are also mutually exclusive, meaning that only one can be true at a time.
Alternative hypotheses often include phrases such as “an effect,” “a difference,” or “a relationship.” When alternative hypotheses are written in mathematical terms, they always include an inequality (usually ≠, but sometimes < or >). As with null hypotheses, there are many acceptable ways to phrase an alternative hypothesis.
Examples of alternative hypotheses
The table below gives examples of research questions and alternative hypotheses to help you get started with formulating your own.
| Does tooth flossing affect the number of cavities? | Tooth flossing has an on the number of cavities. | test: The mean number of cavities per person differs between the flossing group (µ ) and the non-flossing group (µ ) in the population; µ ≠ µ . |
| Does the amount of text highlighted in a textbook affect exam scores? | The amount of text highlighted in the textbook has an on exam scores. | : There is a relationship between the amount of text highlighted and exam scores in the population; β ≠ 0. |
| Does daily meditation decrease the incidence of depression? | Daily meditation the incidence of depression. | test: The proportion of people with depression in the daily-meditation group ( ) is less than the no-meditation group ( ) in the population; < . |
Null and alternative hypotheses are similar in some ways:
- They’re both answers to the research question.
- They both make claims about the population.
- They’re both evaluated by statistical tests.
However, there are important differences between the two types of hypotheses, summarized in the following table.
| A claim that there is in the population. | A claim that there is in the population. | |
|
| ||
| Equality symbol (=, ≥, or ≤) | Inequality symbol (≠, <, or >) | |
| Rejected | Supported | |
| Failed to reject | Not supported |
To help you write your hypotheses, you can use the template sentences below. If you know which statistical test you’re going to use, you can use the test-specific template sentences. Otherwise, you can use the general template sentences.
General template sentences
The only thing you need to know to use these general template sentences are your dependent and independent variables. To write your research question, null hypothesis, and alternative hypothesis, fill in the following sentences with your variables:
Does independent variable affect dependent variable ?
- Null hypothesis ( H 0 ): Independent variable does not affect dependent variable.
- Alternative hypothesis ( H a ): Independent variable affects dependent variable.
Test-specific template sentences
Once you know the statistical test you’ll be using, you can write your hypotheses in a more precise and mathematical way specific to the test you chose. The table below provides template sentences for common statistical tests.
| ( ) | ||
| test
with two groups | The mean dependent variable does not differ between group 1 (µ ) and group 2 (µ ) in the population; µ = µ . | The mean dependent variable differs between group 1 (µ ) and group 2 (µ ) in the population; µ ≠ µ . |
| with three groups | The mean dependent variable does not differ between group 1 (µ ), group 2 (µ ), and group 3 (µ ) in the population; µ = µ = µ . | The mean dependent variable of group 1 (µ ), group 2 (µ ), and group 3 (µ ) are not all equal in the population. |
| There is no correlation between independent variable and dependent variable in the population; ρ = 0. | There is a correlation between independent variable and dependent variable in the population; ρ ≠ 0. | |
| There is no relationship between independent variable and dependent variable in the population; β = 0. | There is a relationship between independent variable and dependent variable in the population; β ≠ 0. | |
| Two-proportions test | The dependent variable expressed as a proportion does not differ between group 1 ( ) and group 2 ( ) in the population; = . | The dependent variable expressed as a proportion differs between group 1 ( ) and group 2 ( ) in the population; ≠ . |
Note: The template sentences above assume that you’re performing one-tailed tests . One-tailed tests are appropriate for most studies.
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
- Normal distribution
- Descriptive statistics
- Measures of central tendency
- Correlation coefficient
Methodology
- Cluster sampling
- Stratified sampling
- Types of interviews
- Cohort study
- Thematic analysis
Research bias
- Implicit bias
- Cognitive bias
- Survivorship bias
- Availability heuristic
- Nonresponse bias
- Regression to the mean
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.
Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.
The null hypothesis is often abbreviated as H 0 . When the null hypothesis is written using mathematical symbols, it always includes an equality symbol (usually =, but sometimes ≥ or ≤).
The alternative hypothesis is often abbreviated as H a or H 1 . When the alternative hypothesis is written using mathematical symbols, it always includes an inequality symbol (usually ≠, but sometimes < or >).
A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (“ x affects y because …”).
A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses . In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Turney, S. (2023, June 22). Null & Alternative Hypotheses | Definitions, Templates & Examples. Scribbr. Retrieved June 24, 2024, from https://www.scribbr.com/statistics/null-and-alternative-hypotheses/
Is this article helpful?

Shaun Turney
Other students also liked, inferential statistics | an easy introduction & examples, hypothesis testing | a step-by-step guide with easy examples, type i & type ii errors | differences, examples, visualizations, what is your plagiarism score.
User Preferences
Content preview.
Arcu felis bibendum ut tristique et egestas quis:
- Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
- Duis aute irure dolor in reprehenderit in voluptate
- Excepteur sint occaecat cupidatat non proident
Keyboard Shortcuts
17.1 - test for homogeneity.
As suggested in the introduction to this lesson, the test for homogeneity is a method, based on the chi-square statistic, for testing whether two or more multinomial distributions are equal. Let's start by trying to get a feel for how our data might "look" if we have two equal multinomial distributions.
Example 17-1 Section

A university admissions officer was concerned that males and females were accepted at different rates into the four different schools (business, engineering, liberal arts, and science) at her university. She collected the following data on the acceptance of 1200 males and 800 females who applied to the university:
| #(Acceptances) | Business | Engineer | Lib Arts | Science | (FIXED) Total |
|---|---|---|---|---|---|
| Male | 300 (25%) | 240 (20%) | 300 (25%) | 360 (30%) | 1200 |
| Female | 200 (25%) | 160 (20%) | 200 (25%) | 240 (30%) | 800 |
| Total | 500 (25%) | 400 (20%) | 500 (25%) | 600 (30%) | 2000 |
Are males and females distributed equally among the various schools?
Let's start by focusing on the business school. We can see that, of the 1200 males who applied to the university, 300 (or 25%) were accepted into the business school. Of the 800 females who applied to the university, 200 (or 25%) were accepted into the business school. So, the business school looks to be in good shape, as an equal percentage of males and females, namely 25%, were accepted into it.
Now, for the engineering school. We can see that, of the 1200 males who applied to the university, 240 (or 20%) were accepted into the engineering school. Of the 800 females who applied to the university, 160 (or 20%) were accepted into the engineering school. So, the engineering school also looks to be in good shape, as an equal percentage of males and females, namely 20%, were accepted into it.
We probably don't have to drag this out any further. If we look at each column in the table, we see that the proportion of males accepted into each school is the same as the proportion of females accepted into each school... which therefore happens to equal the proportion of students accepted into each school, regardless of gender. Therefore, we can conclude that males and females are distributed equally among the four schools.
Example 17-2 Section

| #(Acceptances) | Business | Engineer | Lib Arts | Science | (FIXED) Total |
|---|---|---|---|---|---|
| Male | 240 (20%) | 480 (40%) | 120 (10%) | 360 (30%) | 1200 |
| Female | 240 (30%) | 80 (10%) | 320 (40%) | 160 (20%) | 800 |
| Total | 480 (24%) | 560 (28%) | 440 (22%) | 520 (26%) | 2000 |
Let's again start by focusing on the business school. In this case, of the 1200 males who applied to the university, 240 (or 20%) were accepted into the business school. And, of the 800 females who applied to the university, 240 (or 30%) were accepted into the business school. So, the business school appears to have different rates of acceptance for males and females, 20% compared to 30%.
Now, for the engineering school. We can see that, of the 1200 males who applied to the university, 480 (or 40%) were accepted into the engineering school. Of the 800 females who applied to the university, only 80 (or 10%) were accepted into the engineering school. So, the engineering school also appears to have different rates of acceptance for males and females, 40% compared to 10%.
Again, there's no need drag this out any further. If we look at each column in the table, we see that the proportion of males accepted into each school is different than the proportion of females accepted into each school... and therefore the proportion of students accepted into each school, regardless of gender, is different than the proportion of males and females accepted into each school. Therefore, we can conclude that males and females are not distributed equally among the four schools.
In the context of the two examples above, it quickly becomes apparent that if we wanted to formally test the hypothesis that males and females are distributed equally among the four schools, we'd want to test the hypotheses:
\(H_0 : p_{MB} =p_{FB} \text{ and } p_{ME} =p_{FE} \text{ and } p_{ML} =p_{FL} \text{ and } p_{MS} =p_{FS}\) \(H_A : p_{MB} \ne p_{FB} \text{ or } p_{ME} \ne p_{FE} \text{ or } p_{ML} \ne p_{FL} \text{ or } p_{MS} \ne p_{FS}\)
- \(p_{Mj}\) is the proportion of males accepted into school j = B , E , L , or S
- \(p_{Fj}\) is the proportion of females accepted into school j = B , E , L , or S
In conducting such a hypothesis test, we're comparing the proportions of two multinomial distributions. Before we can develop the method for conducting such a hypothesis test, that is, for comparing the proportions of two multinomial distributions, we first need to define some notation.
Notation Section

We'll use what I think most statisticians would consider standard notation, namely that:
- The letter i will index the h row categories, and
- The letter j will index the k column categories
(The text reverses the use of the i index and the j index.) That said, let's use the framework of the previous examples to introduce the notation we'll use. That is, rewrite the tables above using the following generic notation:
| #(Acc) | Bus \(\left(j = 1 \right)\) | Eng \(\left(j = 2 \right)\) | L Arts \(\left(j = 3 \right)\) | Sci \(\left(j = 4 \right)\) | (FIXED) Total |
|---|---|---|---|---|---|
| M \(\left(i = 1 \right)\) | \(y_{11} \left(\hat{p}_{11} \right)\) | \(y_{12} \left(\hat{p}_{12} \right)\) | \(y_{13} \left(\hat{p}_{13} \right)\) | \(y_{14} \left(\hat{p}_{14} \right)\) | \(n_{1}=\sum_\limits{j=1}^{k} y_{1 j}\) |
| F \(\left(i = 2 \right)\) | \(y_{21} \left(\hat{p}_{21} \right)\) | \(y_{22} \left(\hat{p}_{22} \right)\) | \(y_{23} \left(\hat{p}_{23} \right)\) | \(y_{24} \left(\hat{p}_{24} \right)\) | \(n_{2}=\sum_\limits{j=1}^{k} y_{2 j}\) |
| Total | \(y_{11} + y_{21} \left(\hat{p}_1 \right)\) | \(y_{12} + y_{22} \left(\hat{p}_2 \right)\) | \(y_{13} + y_{23} \left(\hat{p}_3 \right)\) | \(y_{14} + y_{24} \left(\hat{p}_4 \right)\) | \(n_1 + n_2\) |
- \(y_{ij}\) denoting the number falling into the \(j^{th}\) category of the \(i^{th}\) sample
- \(\hat{p}_{ij}=y_{ij}/n_i\)denoting the proportion in the \(i^{th}\) sample falling into the \(j^{th}\) category
- \(n_i=\sum_{j=1}^{k}y_{ij}\)denoting the total number in the \(i^{th}\) sample
- \( \hat{p}_{j}=(y_{1j}+y_{2j})/(n_1+n_2) \)denoting the (overall) proportion falling into the \(j^{th}\) category
With the notation defined as such, we are now ready to formulate the chi-square test statistic for testing the equality of two multinomial distributions.
The Chi-Square Test Statistic Section
The chi-square test statistic for testing the equality of two multinomial distributions:
\(Q=\sum_{i=1}^{2}\sum_{j=1}^{k}\frac{(y_{ij}- n_i\hat{p}_j)^2}{n_i\hat{p}_j}\)
follows an approximate chi-square distribution with k −1 degrees of freedom. Reject the null hypothesis of equal proportions if Q is large, that is, if:
\(Q \ge \chi_{\alpha, k-1}^{2}\)
For the sake of concreteness, let's again use the framework of our example above to derive the chi-square test statistic. For one of the samples, say for the males, we know that:
\(\sum_{j=1}^{k}\frac{(\text{observed }-\text{ expected})^2}{\text{expected}}=\sum_{j=1}^{k}\frac{(y_{1j}- n_1p_{1j})^2}{n_1p_{1j}} \)
follows an approximate chi-square distribution with k −1 degrees of freedom. For the other sample, that is, for the females, we know that:
\(\sum_{j=1}^{k}\frac{(\text{observed }-\text{ expected})^2}{\text{expected}}=\sum_{j=1}^{k}\frac{(y_{2j}- n_2p_{2j})^2}{n_2p_{2j}} \)
follows an approximate chi-square distribution with k −1 degrees of freedom. Therefore, by the independence of two samples, we can "add up the chi-squares," that is:
\(\sum_{i=1}^{2}\sum_{j=1}^{k}\frac{(y_{ij}- n_ip_{ij})^2}{n_ip_{ij}}\)
follows an approximate chi-square distribution with k −1+ k −1 = 2( k −1) degrees of freedom.
Oops.... but we have a problem! The \(p_{ij}\)'s are unknown to us. Of course, we know by now that the solution is to estimate the \(p_{ij}\)'s. Now just how to do that? Well, if the null hypothesis is true, the proportions are equal, that is, if:
\(p_{11}=p_{21}, p_{21}=p_{22}, ... , p_{1k}=p_{2k} \)
we would be best served by using all of the data across the sample categories. That is, the best estimate for each\(j^{th}\) category is the pooled estimate:
\(\hat{p}_j=\frac{y_{1j}+y_{2j}}{n_1+n_2}\)
We also know by now that because we are estimating some paremeters, we have to adjust the degrees of freedom. The pooled estimates \(\hat{p}_j\) estimate the true unknown proportions \(p_{1j} = p_{2j} = p_j\). Now, if we know the first k −1 estimates, that is, if we know:
\(\hat{p}_1, \hat{p}_2, ... , \hat{p}_{k-1}\)
then the \(k^{th}\) one, that is \(\hat{p}_k\), is determined because:
\(\sum_{j=1}^{k}\hat{p}_j=1\)
\(\hat{p}_k=1-(\hat{p}_1+\hat{p}_2+ ... + \hat{p}_{k-1})\)
So, we are estimating k −1 parameters, and therefore we have to subtract k −1 from the degrees of freedom. Doing so, we get that
follows an approximate chi-square distribution with 2( k −1) − ( k −1) = k − 1 degrees of freedom. As was to be proved!
Note Section
Our only example on this page has involved \(h = 2\) samples. If there are more than two samples, that is, if \(h > 2\), then the definition of the chi-square statistic is appropriately modified. That is:
\(Q=\sum_{i=1}^{h}\sum_{j=1}^{k}\frac{(y_{ij}- n_i\hat{p}_j)^2}{n_i\hat{p}_j}\)
follows an approximate chi-square distribution with \(h(k−1) − (k−1) = (h−1)(k − 1)\) degrees of freedom.
Let's take a look at another example.
Example 17-3 Section
The head of a surgery department at a university medical center was concerned that surgical residents in training applied unnecessary blood transfusions at a different rate than the more experienced attending physicians. Therefore, he ordered a study of the 49 Attending Physicians and 71 Residents in Training with privileges at the hospital. For each of the 120 surgeons, the number of blood transfusions prescribed unnecessarily in a one-year period was recorded. Based on the number recorded, a surgeon was identified as either prescribing unnecessary blood transfusions Frequently, Occasionally, Rarely, or Never. Here's a summary table (or " contingency table ") of the resulting data:
| Physician | Frequent | Occasionally | Rarely | Never | Total |
|---|---|---|---|---|---|
| Attending | 2 (4.1%) | 3 (6.1%) | 31 (63.3%) | 13 (26.5%) | 49 |
| Resident | 15 (21.1%) | 28 (39.4%) | 23 (32.4%) | 5 (7.0%) | 71 |
| Total | 17 | 31 | 54 | 18 | 120 |
Are attending physicians and residents in training distributed equally among the various unnecessary blood transfusion categories?
We are interested in testing the null hypothesis:
\(H_0 : p_{RF} =p_{AF} \text{ and } p_{RO} =p_{AO} \text{ and } p_{RR} =p_{AR} \text{ and } p_{RN} =p_{AN}\)
against the alternative hypothesis:
\(H_A : p_{RF} \ne p_{AF} \text{ or } p_{RO} \ne p_{AO} \text{ or } p_{RR} \ne p_{AR} \text{ or } p_{RN} \ne p_{AN}\)
The observed data were given to us in the table above. So, the next thing we need to do is find the expected counts for each cell of the table:
| Physician | Frequent | Occasionally | Rarely | Never | Total |
|---|---|---|---|---|---|
| Attending | 49 | ||||
| Resident | 71 | ||||
| Total | 17 | 31 | 54 | 18 | 120 |
It is in the calculation of the expected values that you can readily see why we have (2−1)(4−1) = 3 degrees of freedom in this case. That's because, we only have to calculate three of the cells directly.
| Physician | Frequent | Occasionally | Rarely | Never | Total |
|---|---|---|---|---|---|
| Attending | 6.942 | 12.658 | 22.05 | 49 | |
| Resident | 71 | ||||
| Total | 17 | 31 | 54 | 18 | 120 |
Once we do that, the remaining five cells can be calculated by way of subtraction:
| Physician | Frequent | Occasionally | Rarely | Never | Total |
|---|---|---|---|---|---|
| Attending | 6.942 | 12.658 | 22.05 | 7.35 | 49 |
| Resident | 10.058 | 18.342 | 31.95 | 10.65 | 71 |
| Total | 17 | 31 | 54 | 18 | 120 |
Now that we have the observed and expected counts, calculating the chi-square statistic is a straightforward exercise:
\(Q=\frac{(2-6.942)^2}{6.942}+ ... +\frac{(5-10.65)^2}{10.65} =31.88 \)
The chi-square test tells us to reject the null hypothesis, at the 0.05 level, if Q is greater than a chi-square random variable with 3 degrees of freedom, that is, if \(Q > 7.815\). Because \(Q = 31.88 > 7.815\), we reject the null hypothesis. There is sufficient evidence at the 0.05 level to conclude that the distribution of unnecessary transfusions differs among attending physicians and residents.
Minitab ®
Using minitab section .
- Enter the data (in the inside of the frequency table only) into the columns of the worksheet
- Select Stat >> Tables >> Chi-square test
then you'll get typical chi-square test output that looks something like this:
| Freq | Occ | Rare | Never | Total | |
|---|---|---|---|---|---|
| 1 | 2 6.94 | 3 12.66 | 31 22.05 | 13 7.35 | 49 |
| 2 | 15 10.06 | 28 18.34 | 23 31.95 | 5 10.65 | 71 |
| Total | 17 | 31 | 54 | 18 | 120 |
Chi- sq = 3.518 + 7.369 + 3.633 + 4.343 +
2.428 + 5.086 + 2.507 + 2.997 = 31.881
DF = 3, P-Value = 0.000
Teach yourself statistics
Chi-Square Test of Homogeneity
This lesson explains how to conduct a chi-square test of homogeneity . The test is applied to a single categorical variable from two or more different populations. It is used to determine whether frequency counts are distributed identically across different populations.
For example, in a survey of TV viewing preferences, we might ask respondents to identify their favorite program. We might ask the same question of two different populations, such as males and females. We could use a chi-square test for homogeneity to determine whether male viewing preferences differed significantly from female viewing preferences. The sample problem at the end of the lesson considers this example.
When to Use Chi-Square Test for Homogeneity
The test procedure described in this lesson is appropriate when the following conditions are met:
- For each population, the sampling method is simple random sampling .
- The variable under study is categorical .
- If sample data are displayed in a contingency table (Populations x Category levels), the expected frequency count for each cell of the table is at least 5.
This approach consists of four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results.
State the Hypotheses
Every hypothesis test requires the analyst to state a null hypothesis and an alternative hypothesis . The hypotheses are stated in such a way that they are mutually exclusive. That is, if one is true, the other must be false; and vice versa.
Suppose that data were sampled from r populations, and assume that the categorical variable had c levels. At any specified level of the categorical variable, the null hypothesis states that each population has the same proportion of observations. Thus,
| H : P = P = . . . = P |
The alternative hypothesis (H a ) is that at least one of the null hypothesis statements is false.
Formulate an Analysis Plan
The analysis plan describes how to use sample data to accept or reject the null hypothesis. The plan should specify the following elements.
- Significance level. Often, researchers choose significance levels equal to 0.01, 0.05, or 0.10; but any value between 0 and 1 can be used.
- Test method. Use the chi-square test for homogeneity to determine whether observed sample frequencies differ significantly from expected frequencies specified in the null hypothesis. The chi-square test for homogeneity is described in the next section.
Analyze Sample Data
Using sample data from the contingency tables, find the degrees of freedom, expected frequency counts, test statistic, and the P-value associated with the test statistic. The analysis described in this section is illustrated in the sample problem at the end of this lesson.
DF = (r - 1) * (c - 1)
E r,c = (n r * n c ) / n
Χ 2 = Σ [ (O r,c - E r,c ) 2 / E r,c ]
- P-value. The P-value is the probability of observing a sample statistic as extreme as the test statistic. Since the test statistic is a chi-square, use the Chi-Square Distribution Calculator to assess the probability associated with the test statistic. Use the degrees of freedom computed above.
Interpret Results
If the sample findings are unlikely, given the null hypothesis, the researcher rejects the null hypothesis. Typically, this involves comparing the P-value to the significance level , and rejecting the null hypothesis when the P-value is less than the significance level.
Test Your Understanding
In a study of the television viewing habits of children, a developmental psychologist selects a random sample of 300 first graders - 100 boys and 200 girls. Each child is asked which of the following TV programs they like best: The Lone Ranger, Sesame Street, or The Simpsons. Results are shown in the contingency table below.
| Viewing Preferences | Total | |||
|---|---|---|---|---|
| Lone RangerLone Ranger | Sesame StreetSesame Street | The SimpsonsThe Simpsons | ||
| Boys | 50 | 30 | 20 | 100 |
| Girls | 50 | 80 | 70 | 200 |
| Total | 100 | 110 | 90 | 300 |
Do the boys' preferences for these TV programs differ significantly from the girls' preferences? Use a 0.05 level of significance.
The solution to this problem takes four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results. We work through those steps below:
State the hypotheses. The first step is to state the null hypothesis and an alternative hypothesis.
| H : P = P H : P = P H : P = P |
- Alternative hypothesis: At least one of the null hypothesis statements is false.
- Formulate an analysis plan . For this analysis, the significance level is 0.05. Using sample data, we will conduct a chi-square test for homogeneity .
DF = (r - 1) * (c - 1) DF = (r - 1) * (c - 1) = (2 - 1) * (3 - 1) = 2
E r,c = (n r * n c ) / n E 1,1 = (100 * 100) / 300 = 10000/300 = 33.3 E 1,2 = (100 * 110) / 300 = 11000/300 = 36.7 E 1,3 = (100 * 90) / 300 = 9000/300 = 30.0 E 2,1 = (200 * 100) / 300 = 20000/300 = 66.7 E 2,2 = (200 * 110) / 300 = 22000/300 = 73.3 E 2,3 = (200 * 90) / 300 = 18000/300 = 60.0
Χ 2 = Σ[ (O r,c - E r,c ) 2 / E r,c ] Χ 2 = (50 - 33.3) 2 /33.3 + (30 - 36.7) 2 /36.7 + (20 - 30) 2 /30 + (50 - 66.7) 2 /66.7 + (80 - 73.3) 2 /73.3 + (70 - 60) 2 /60 Χ 2 = (16.7) 2 /33.3 + (-6.7) 2 /36.7 + (-10.0) 2 /30 + (-16.7) 2 /66.7 + (3.3) 2 /73.3 + (10) 2 /60 Χ 2 = 8.38 + 1.22 + 3.33 + 4.18 + 0.61 + 1.67 = 19.39
where DF is the degrees of freedom, r is the number of populations, c is the number of levels of the categorical variable, n r is the number of observations from population r , n c is the number of observations from level c of the categorical variable, n is the number of observations in the sample, E r,c is the expected frequency count in population r for level c , and O r,c is the observed frequency count in population r for level c .
The P-value is the probability that a chi-square statistic having 2 degrees of freedom is more extreme than 19.39. We use the Chi-Square Distribution Calculator to find P(Χ 2 > 19.39) = 0.00006.
- Interpret results . Since the P-value (0.00006) is less than the significance level (0.05), we reject the null hypothesis.
Note: If you use this approach on an exam, you may also want to mention why this approach is appropriate. Specifically, the approach is appropriate because the sampling method was simple random sampling, the variable under study was categorical, and the expected frequency count was at least 5 in each population at each level of the categorical variable.

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

12.13: Test of Homogeneity
- Last updated
- Save as PDF
- Page ID 251470
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
Learning Objectives
- Conduct a chi-square test of homogeneity. Interpret the conclusion in context.
We have learned the details for two chi-square tests, the goodness-of-fit test, and the test of independence. Now we focus on the third and last chi-square test that we will learn, the test for homogeneity . This test determines if two or more populations (or subgroups of a population) have the same distribution of a single categorical variable.
The test of homogeneity expands the test for a difference in two population proportions, which is the two-proportion Z-test we learned in Inference for Two Proportions . We use the two-proportion Z-test when the response variable has only two outcome categories and we are comparing two populations (or two subgroups.) We use the test of homogeneity if the response variable has two or more categories and we wish to compare two or more populations (or subgroups.)
We can answer the following research questions with a chi-square test of homogeneity:
- Does the use of steroids in collegiate athletics differ across the three NCAA divisions?
- Was the distribution of political views (liberal, moderate, conservative) different for last three presidential elections in the United States?
The null hypothesis states that the distribution of the categorical variable is the same for the populations (or subgroups). In other words, the proportion with a given response is the same in all of the populations, and this is true for all response categories. The alternative hypothesis says that the distributions differ.
Note: Homogeneous means the same in structure or composition. This test gets its name from the null hypothesis, where we claim that the distribution of the responses are the same (homogeneous) across groups.
To test our hypotheses, we select a random sample from each population and gather data on one categorical variable. As with all chi-square tests, the expected counts reflect the null hypothesis. We must determine what we expect to see in each sample if the distributions are identical. As before, the chi-square test statistic measures the amount that the observed counts in the samples deviate from the expected counts.
Steroid Use in Collegiate Sports
In 2006, the NCAA published a report called “Substance Use: NCAA Study of Substance Use of College Student-Athletes.” We use data from this report to investigate the following question: Does steroid use by student athletes differ for the three NCAA divisions?
The data comes from a random selection of teams in each NCAA division. The sampling plan was somewhat complex, but we can view the data as though it came from a random sample of athletes in each division. The surveys are anonymous to encourage truthful responses.
To see the NCAA report on substance use, click here .
Step 1: State the hypotheses.
In the test of homogeneity, the null hypothesis says that the distribution of a categorical response variable is the same in each population. In this example, the categorical response variable is steroid use (yes or no). The populations are the three NCAA divisions.
- H 0 : The proportion of athletes using steroids is the same in each of the three NCAA divisions.
- H a : The proportion of athletes using steroids is not same in each of the three NCAA divisions.
Note: These hypotheses imply that the proportion of athletes not using steroids is also the same in each of the three NCAA divisions, so we don’t need to state this explicitly. For example, if 2% of the athletes in each division are using steroids, then 98% are not.
Here is an alternative way we could state the hypotheses for a test of homogeneity.
- H 0 : For each of the three NCAA divisions, the distribution of “yes” and “no” responses to the question about steroid use is the same.
- H a : The distribution of responses is not the same.
Step 2: Collect and analyze the data.
We summarized the data from these three samples in a two-way table.
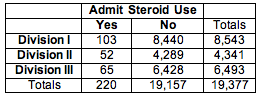
We use percentages to compare the distributions of yes and no responses in the three samples. This step is similar to our data analysis for the test of independence.
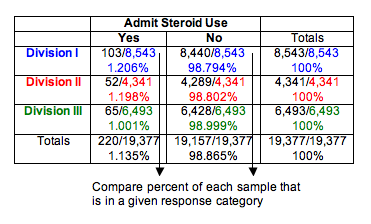
We can see that Division I and Division II schools have essentially the same percentage of athletes who admit steroid use (about 1.2%). Not surprisingly, the least competitive division, Division III, has a slightly lower percentage (about 1.0%). Do these results suggest that the proportion of athletes using steroids is the same for the three divisions? Or is the difference seen in the sample of Division III schools large enough to suggest differences in the divisions? After all, the sample sizes are very large. We know that for large samples, a small difference can be statistically significant. Of course, we have to conduct the test of homogeneity to find out.
Note: We decided not to use ribbon charts for visual comparison of the three distributions because the percentage admitting steroid use is too small in each sample to be visible.
Step 3: Assess the evidence.
We need to determine the expected values and the chi-square test statistic so that we can find the P-value.
Calculating Expected Values for a Test of Homogeneity
Expected counts always describe what we expect to see in a sample if the null hypothesis is true. In this situation, we expect the percentage using steroids to be the same for each division. What percentage do we use? We find the percentage using steroids in the combined samples. This calculation is the same as we did when finding expected counts for a test of independence, though the logic of the calculation is subtly different.
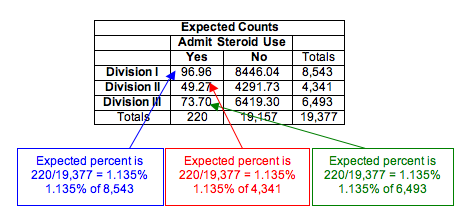
Here are the calculations for the response “yes”:
- Percentage using steroids in combined samples: 220/19,377 = 0.01135 = 1.135%
Expected count of steroid users for Division I is 1.135% of Division I sample:
- 0.01135(8,543) = 96.96
Expected count of steroid users for Division II is 1.135% of Division II sample:
- 0.01135(4,341) = 49.27
Expected count of steroid users for Division III is 1.135% of Division III sample:
- 0.01135(6,493) = 73.70
Checking Conditions
The conditions for use of the chi-square distribution are the same as we learned previously:
- A sample is randomly selected from each population.
- All of the expected counts are 5 or greater.
Since this data meets the conditions, we can proceed with calculating the χ 2 test statistic.
Calculating the Chi-Square Test Statistic
There are no changes in the way we calculate the chi-square test statistic.
We use technology to calculate the chi-square value. For this example, we show the calculation. There are six terms, one for each cell in the 3 × 2 table. (We ignore the totals, as always.)

Finding Degrees of Freedom and the P-Value
For chi-square tests based on two-way tables (both the test of independence and the test of homogeneity), the degrees of freedom are ( r − 1)( c − 1), where r is the number of rows and c is the number of columns in the two-way table (not counting row and column totals). In this case, the degrees of freedom are (3 − 1)(2 − 1) = 2.
We use the chi-square distribution with df = 2 to find the P-value. The P-value is large (0.4561), so we fail to reject the null hypothesis.
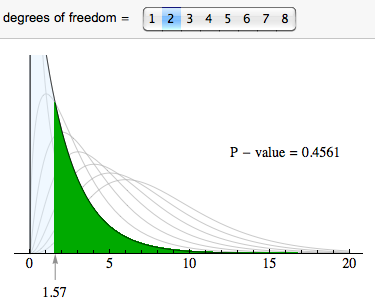
Step 4: Conclusion.
The data does not provide strong enough evidence to conclude that steroid use differs in the three NCAA divisions (P-value = 0.4561).
Learn By Doing
First use of anabolic steroids by ncaa athletes.
The NCAA survey includes this question: “When, if ever, did you start using anabolic steroids?” The response options are: have never used, before junior high, junior high, high school, freshman year of college, after freshman year of college. We focused on those who admitted use of steroids and compared the distribution of their responses for the years 1997, 2001, and 2005. (These are the years that the NCAA conducted the survey. Counts are estimates from reported percentages and sample size.) Recall that the NCAA uses random sampling in its sampling design.
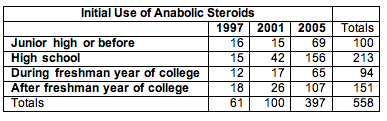
Please click here to open the simulation for use in the following activity.
https://assessments.lumenlearning.co...sessments/3798
https://assessments.lumenlearning.co...sessments/3799
https://assessments.lumenlearning.co...sessments/3730
https://assessments.lumenlearning.co...sessments/3731
https://assessments.lumenlearning.co...sessments/3800
https://assessments.lumenlearning.co...sessments/3801
https://assessments.lumenlearning.co...sessments/3802
https://assessments.lumenlearning.co...sessments/3803
We now know the details for the chi-square test for homogeneity. We conclude with two activities that will give you practice recognizing when to use this test.
Gender and Politics
Consider these two situations:
- A: Liberal, moderate, or conservative: Are there differences in political views of men and women in the United States? We survey a random sample of 100 U.S. men and 100 U.S. women.
- B: Do you plan to vote in the next presidential election? We ask a random sample of 100 U.S. men and 100 U.S. women. We look for differences in the proportion of men and women planning to vote.
https://assessments.lumenlearning.co...sessments/3732
https://assessments.lumenlearning.co...sessments/3733
Steroid Use for Male Athletes in NCAA Sports
We plan to compare steroid use for male athletes in NCAA baseball, basketball, and football. We design two different sampling plans.
- A: Survey distinct random samples of NCAA athletes from each sport: 500 baseball players, 400 basketball players, 900 football players.
- B. Survey a random sample of 1,800 NCAA male athletes and categorize players by sport and admitted steroid use. Responses are anonymous.
https://assessments.lumenlearning.co...sessments/3734
Let’s Summarize
In “Chi-Square Tests for Two-Way Tables,” we discussed two different hypothesis tests using the chi-square test statistic:
- Test of independence for a two-way table
- Test of homogeneity for a two-way table
Test of Independence for a Two-Way Table
- In the test of independence, we consider one population and two categorical variables.
- In Probability and Probability Distribution , we learned that two events are independent if P ( A | B ) = P ( A ), but we did not pay attention to variability in the sample. With the chi-square test of independence, we have a method for deciding whether our observed P ( A | B ) is “too far” from our observed P ( A ) to infer independence in the population.
- The null hypothesis says the two variables are independent (or not associated). The alternative hypothesis says the two variables are dependent (or associated).
- To test our hypotheses, we select a single random sample and gather data for two different categorical variables.
- Example: Do men and women differ in their perception of their weight? Select a random sample of adults. Ask them two questions: (1) Are you male or female? (2) Do you feel that you are overweight, underweight, or about right in weight?
Test of Homogeneity for a Two-Way Table
- In the test of homogeneity, we consider two or more populations (or two or more subgroups of a population) and a single categorical variable.
- The test of homogeneity expands on the test for a difference in two population proportions that we learned in Inference for Two Proportions by comparing the distribution of the categorical variable across multiple groups or populations.
- The null hypothesis says that the distribution of proportions for all categories is the same in each group or population. The alternative hypothesis says that the distributions differ.
- To test our hypotheses, we select a random sample from each population or subgroup independently. We gather data for one categorical variable.
- Example: Is the rate of steroid use different for different men’s collegiate sports (baseball, basketball, football, tennis, track/field)? Randomly select a sample of athletes from each sport and ask them anonymously if they use steroids.
The difference between these two tests is subtle. They differ primarily in study design. In the test of independence, we select individuals at random from a population and record data for two categorical variables. The null hypothesis says that the variables are independent. In the test of homogeneity, we select random samples from each subgroup or population separately and collect data on a single categorical variable. The null hypothesis says that the distribution of the categorical variable is the same for each subgroup or population.
Both tests use the same chi-square test statistic.
The Chi-Square Test Statistic and Distribution
For all chi-square tests, the chi-square test statistic χ 2 is the same. It measures how far the observed data are from the null hypothesis by comparing observed counts and expected counts. Expected counts are the counts we expect to see if the null hypothesis is true.
The chi-square model is a family of curves that depend on degrees of freedom. For a two-way table, the degrees of freedom equals ( r − 1)( c − 1). All chi-square curves are skewed to the right with a mean equal to the degrees of freedom.
A chi-square model is a good fit for the distribution of the chi-square test statistic only if the following conditions are met:
- The sample is randomly selected.
- All expected counts are 5 or greater.
If these conditions are met, we use the chi-square distribution to find the P-value. We use the same logic that we have used in all hypothesis tests to draw a conclusion based on the P-value. If the P-value is at least as small as the significance level, we reject the null hypothesis and accept the alternative hypothesis. The P-value is the likelihood that results from random samples have a χ 2 value equal to or greater than that calculated from the data if the null hypothesis is true.
- Concepts in Statistics. Provided by : Open Learning Initiative. Located at : http://oli.cmu.edu . License : CC BY: Attribution

Chapter 11: The Chi-Square Distribution

11.4 Test for Homogeneity
Learning objectives.
By the end of this section, the student should be able to:
- calculate the test statistic for a test for homogeneity
- test for homogeneity , and draw a conclusion about whether two populations have the same distribution
The goodness–of–fit test can be used to decide whether a population fits a given distribution, but it will not suffice to decide whether two populations follow the same unknown distribution. A different test, called the test for homogeneity , can be used to draw a conclusion about whether two populations have the same distribution. To calculate the test statistic for a test for homogeneity, follow the same procedure as with the test of independence.
The expected value for each cell needs to be at least five in order for you to use this test.
H 0 : The distributions of the two populations are the same.
H a : The distributions of the two populations are not the same.
Test Statistic: Use a [latex]{\chi }^{2}[/latex] test statistic. It is computed in the same way as the test for independence.
Degrees of Freedom ( df ) df = number of columns – 1
Requirements: All values in the table must be greater than or equal to five.
Common Uses: Comparing two populations. For example: men vs. women, before vs. after, east vs. west. The variable is categorical with more than two possible response values.
Do male and female college students have the same distribution of living arrangements? Use a level of significance of 0.05. Suppose that 250 randomly selected male college students and 300 randomly selected female college students were asked about their living arrangements: dormitory, apartment, with parents, other. The results are shown in [link] . Do male and female college students have the same distribution of living arrangements?
| Dormitory | Apartment | With Parents | Other | |
| Males | 72 | 84 | 49 | 45 |
| Females | 91 | 86 | 88 | 35 |
H0: The distribution of living arrangements for male college students is the same as the distribution of living arrangements for female college students.
Ha: The distribution of living arrangements for male college students is not the same as the distribution of living arrangements for female college students.
Degrees of Freedom (df):
df = number of columns – 1 = 4 – 1 = 3
Distribution for the test:[latex]{\chi }_{3}^{2}[/latex]
Calculate the test statistic: χ2 = 10.1287 (calculator or computer)
Probability statement: p-value = P(χ2 >10.1287) = 0.0175
Press the MATRX key and arrow over to EDIT. Press 1:[A]. Press 2 ENTER 4 ENTER. Enter the table values by row. Press ENTER after each. Press 2nd QUIT. Press STAT and arrow over to TESTS. Arrow down to C:χ2-TEST. Press ENTER. You should see Observed:[A] and Expected:[B]. Arrow down to Calculate. Press ENTER. The test statistic is 10.1287 and the p-value = 0.0175. Do the procedure a second time but arrow down to Draw instead of calculate.
Compare α and the p-value: Since no α is given, assume α = 0.05. p-value = 0.0175. α > p-value.
Make a decision: Since α > p-value, reject H0. This means that the distributions are not the same.
Conclusion: At a 5% level of significance, from the data, there is sufficient evidence to conclude that the distributions of living arrangements for male and female college students are not the same.
Notice that the conclusion is only that the distributions are not the same. We cannot use the test for homogeneity to draw any conclusions about how they differ.
Do families and singles have the same distribution of cars? Use a level of significance of 0.05. Suppose that 100 randomly selected families and 200 randomly selected singles were asked what type of car they drove: sport, sedan, hatchback, truck, van/SUV. The results are shown in [link] . Do families and singles have the same distribution of cars? Test at a level of significance of 0.05.
| Sport | Sedan | Hatchback | Truck | Van/SUV | |
|---|---|---|---|---|---|
| Family | 5 | 15 | 35 | 17 | 28 |
| Single | 45 | 65 | 37 | 46 | 7 |
With a p -value of almost zero, we reject the null hypothesis. The data show that the distribution of cars is not the same for families and singles.
Both before and after a recent earthquake, surveys were conducted asking voters which of the three candidates they planned on voting for in the upcoming city council election. Has there been a change since the earthquake? Use a level of significance of 0.05. [link] shows the results of the survey. Has there been a change in the distribution of voter preferences since the earthquake?
| Perez | Chung | Stevens | |
| Before | 167 | 128 | 135 |
| After | 214 | 197 | 225 |
H0: The distribution of voter preferences was the same before and after the earthquake.
Ha: The distribution of voter preferences was not the same before and after the earthquake.
df = number of columns – 1 = 3 – 1 = 2
Distribution for the test: [latex]{\chi }_{2}^{2}[/latex]
Calculate the test statistic: χ2 = 3.2603 (calculator or computer)
Probability statement: p-value=P(χ2 > 3.2603) = 0.1959
Press the MATRX key and arrow over to EDIT. Press 1:[A]. Press 2 ENTER 3 ENTER. Enter the table values by row. Press ENTER after each. Press 2nd QUIT. Press STAT and arrow over to TESTS. Arrow down to C:χ2-TEST. Press ENTER. You should see Observed:[A] and Expected:[B]. Arrow down to Calculate. Press ENTER. The test statistic is 3.2603 and the p-value = 0.1959. Do the procedure a second time but arrow down to Draw instead of calculate.
Compare α and the p-value:α = 0.05 and the p-value = 0.1959. α < p-value.
Make a decision: Since α < p-value, do not reject Ho.
Conclusion: At a 5% level of significance, from the data, there is insufficient evidence to conclude that the distribution of voter preferences was not the same before and after the earthquake.
Ivy League schools receive many applications, but only some can be accepted. At the schools listed in [link] , two types of applications are accepted: regular and early decision.
| Application Type Accepted | Brown | Columbia | Cornell | Dartmouth | Penn | Yale |
|---|---|---|---|---|---|---|
| Regular | 2,115 | 1,792 | 5,306 | 1,734 | 2,685 | 1,245 |
| Early Decision | 577 | 627 | 1,228 | 444 | 1,195 | 761 |
We want to know if the number of regular applications accepted follows the same distribution as the number of early applications accepted. State the null and alternative hypotheses, the degrees of freedom and the test statistic, sketch the graph of the p -value, and draw a conclusion about the test of homogeneity.
H 0 : The distribution of regular applications accepted is the same as the distribution of early applications accepted.
H a : The distribution of regular applications accepted is not the same as the distribution of early applications accepted.
df = 5
χ 2 test statistic = 430.06
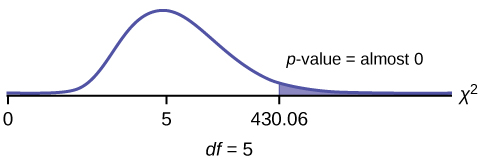
Press the MATRX key and arrow over to EDIT . Press 1:[A] . Press 3 ENTER 3 ENTER . Enter the table values by row. Press ENTER after each. Press 2nd QUIT . Press STAT and arrow over to TESTS . Arrow down to C:χ2-TEST . Press ENTER . You should see Observed:[A] and Expected:[B] . Arrow down to Calculate . Press ENTER . The test statistic is 430.06 and the p -value = 9.80E-91. Do the procedure a second time but arrow down to Draw instead of calculate .
Data from the Insurance Institute for Highway Safety, 2013. Available online at www.iihs.org/iihs/ratings (accessed May 24, 2013).
“Energy use (kg of oil equivalent per capita).” The World Bank, 2013. Available online at http://data.worldbank.org/indicator/EG.USE.PCAP.KG.OE/countries (accessed May 24, 2013).
“Parent and Family Involvement Survey of 2007 National Household Education Survey Program (NHES),” U.S. Department of Education, National Center for Education Statistics. Available online at http://nces.ed.gov/pubsearch/pubsinfo.asp?pubid=2009030 (accessed May 24, 2013).
“Parent and Family Involvement Survey of 2007 National Household Education Survey Program (NHES),” U.S. Department of Education, National Center for Education Statistics. Available online at http://nces.ed.gov/pubs2009/2009030_sup.pdf (accessed May 24, 2013).
Introductory Statistics Copyright © 2024 by LOUIS: The Louisiana Library Network is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License , except where otherwise noted.
Share This Book

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

8.1.1: Null and Alternative Hypotheses
- Last updated
- Save as PDF
- Page ID 10971

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.
\(H_0\): The null hypothesis: It is a statement of no difference between the variables—they are not related. This can often be considered the status quo and as a result if you cannot accept the null it requires some action.
\(H_a\): The alternative hypothesis: It is a claim about the population that is contradictory to \(H_0\) and what we conclude when we reject \(H_0\). This is usually what the researcher is trying to prove.
Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.
After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are "reject \(H_0\)" if the sample information favors the alternative hypothesis or "do not reject \(H_0\)" or "decline to reject \(H_0\)" if the sample information is insufficient to reject the null hypothesis.
| equal (=) | not equal \((\neq)\) greater than (>) less than (<) |
| greater than or equal to \((\geq)\) | less than (<) |
| less than or equal to \((\geq)\) | more than (>) |
\(H_{0}\) always has a symbol with an equal in it. \(H_{a}\) never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.
Example \(\PageIndex{1}\)
- \(H_{0}\): No more than 30% of the registered voters in Santa Clara County voted in the primary election. \(p \leq 30\)
- \(H_{a}\): More than 30% of the registered voters in Santa Clara County voted in the primary election. \(p > 30\)
Exercise \(\PageIndex{1}\)
A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.
- \(H_{0}\): The drug reduces cholesterol by 25%. \(p = 0.25\)
- \(H_{a}\): The drug does not reduce cholesterol by 25%. \(p \neq 0.25\)
Example \(\PageIndex{2}\)
We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:
- \(H_{0}: \mu = 2.0\)
- \(H_{a}: \mu \neq 2.0\)
Exercise \(\PageIndex{2}\)
We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol \((=, \neq, \geq, <, \leq, >)\) for the null and alternative hypotheses.
- \(H_{0}: \mu \_ 66\)
- \(H_{a}: \mu \_ 66\)
- \(H_{0}: \mu = 66\)
- \(H_{a}: \mu \neq 66\)
Example \(\PageIndex{3}\)
We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:
- \(H_{0}: \mu \geq 5\)
- \(H_{a}: \mu < 5\)
Exercise \(\PageIndex{3}\)
We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- \(H_{0}: \mu \_ 45\)
- \(H_{a}: \mu \_ 45\)
- \(H_{0}: \mu \geq 45\)
- \(H_{a}: \mu < 45\)
Example \(\PageIndex{4}\)
In an issue of U. S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.
- \(H_{0}: p \leq 0.066\)
- \(H_{a}: p > 0.066\)
Exercise \(\PageIndex{4}\)
On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (\(=, \neq, \geq, <, \leq, >\)) for the null and alternative hypotheses.
- \(H_{0}: p \_ 0.40\)
- \(H_{a}: p \_ 0.40\)
- \(H_{0}: p = 0.40\)
- \(H_{a}: p > 0.40\)
COLLABORATIVE EXERCISE
Bring to class a newspaper, some news magazines, and some Internet articles . In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.
In a hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we:
- Evaluate the null hypothesis , typically denoted with \(H_{0}\). The null is not rejected unless the hypothesis test shows otherwise. The null statement must always contain some form of equality \((=, \leq \text{or} \geq)\)
- Always write the alternative hypothesis , typically denoted with \(H_{a}\) or \(H_{1}\), using less than, greater than, or not equals symbols, i.e., \((\neq, >, \text{or} <)\).
- If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis.
- Never state that a claim is proven true or false. Keep in mind the underlying fact that hypothesis testing is based on probability laws; therefore, we can talk only in terms of non-absolute certainties.
Formula Review
\(H_{0}\) and \(H_{a}\) are contradictory.
| equal \((=)\) | greater than or equal to \((\geq)\) | less than or equal to \((\leq)\) | |
| has: | not equal \((\neq)\) greater than \((>)\) less than \((<)\) | less than \((<)\) | greater than \((>)\) |
- If \(\alpha \leq p\)-value, then do not reject \(H_{0}\).
- If\(\alpha > p\)-value, then reject \(H_{0}\).
\(\alpha\) is preconceived. Its value is set before the hypothesis test starts. The \(p\)-value is calculated from the data.References
Data from the National Institute of Mental Health. Available online at http://www.nimh.nih.gov/publicat/depression.cfm .
An official website of the United States government
The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.
The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.
- Publications
- Account settings
Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .
- Advanced Search
- Journal List
- Indian J Crit Care Med
- v.23(Suppl 3); 2019 Sep
An Introduction to Statistics: Understanding Hypothesis Testing and Statistical Errors
Priya ranganathan.
1 Department of Anesthesiology, Critical Care and Pain, Tata Memorial Hospital, Mumbai, Maharashtra, India
2 Department of Surgical Oncology, Tata Memorial Centre, Mumbai, Maharashtra, India
The second article in this series on biostatistics covers the concepts of sample, population, research hypotheses and statistical errors.
How to cite this article
Ranganathan P, Pramesh CS. An Introduction to Statistics: Understanding Hypothesis Testing and Statistical Errors. Indian J Crit Care Med 2019;23(Suppl 3):S230–S231.
Two papers quoted in this issue of the Indian Journal of Critical Care Medicine report. The results of studies aim to prove that a new intervention is better than (superior to) an existing treatment. In the ABLE study, the investigators wanted to show that transfusion of fresh red blood cells would be superior to standard-issue red cells in reducing 90-day mortality in ICU patients. 1 The PROPPR study was designed to prove that transfusion of a lower ratio of plasma and platelets to red cells would be superior to a higher ratio in decreasing 24-hour and 30-day mortality in critically ill patients. 2 These studies are known as superiority studies (as opposed to noninferiority or equivalence studies which will be discussed in a subsequent article).
SAMPLE VERSUS POPULATION
A sample represents a group of participants selected from the entire population. Since studies cannot be carried out on entire populations, researchers choose samples, which are representative of the population. This is similar to walking into a grocery store and examining a few grains of rice or wheat before purchasing an entire bag; we assume that the few grains that we select (the sample) are representative of the entire sack of grains (the population).
The results of the study are then extrapolated to generate inferences about the population. We do this using a process known as hypothesis testing. This means that the results of the study may not always be identical to the results we would expect to find in the population; i.e., there is the possibility that the study results may be erroneous.
HYPOTHESIS TESTING
A clinical trial begins with an assumption or belief, and then proceeds to either prove or disprove this assumption. In statistical terms, this belief or assumption is known as a hypothesis. Counterintuitively, what the researcher believes in (or is trying to prove) is called the “alternate” hypothesis, and the opposite is called the “null” hypothesis; every study has a null hypothesis and an alternate hypothesis. For superiority studies, the alternate hypothesis states that one treatment (usually the new or experimental treatment) is superior to the other; the null hypothesis states that there is no difference between the treatments (the treatments are equal). For example, in the ABLE study, we start by stating the null hypothesis—there is no difference in mortality between groups receiving fresh RBCs and standard-issue RBCs. We then state the alternate hypothesis—There is a difference between groups receiving fresh RBCs and standard-issue RBCs. It is important to note that we have stated that the groups are different, without specifying which group will be better than the other. This is known as a two-tailed hypothesis and it allows us to test for superiority on either side (using a two-sided test). This is because, when we start a study, we are not 100% certain that the new treatment can only be better than the standard treatment—it could be worse, and if it is so, the study should pick it up as well. One tailed hypothesis and one-sided statistical testing is done for non-inferiority studies, which will be discussed in a subsequent paper in this series.
STATISTICAL ERRORS
There are two possibilities to consider when interpreting the results of a superiority study. The first possibility is that there is truly no difference between the treatments but the study finds that they are different. This is called a Type-1 error or false-positive error or alpha error. This means falsely rejecting the null hypothesis.
The second possibility is that there is a difference between the treatments and the study does not pick up this difference. This is called a Type 2 error or false-negative error or beta error. This means falsely accepting the null hypothesis.
The power of the study is the ability to detect a difference between groups and is the converse of the beta error; i.e., power = 1-beta error. Alpha and beta errors are finalized when the protocol is written and form the basis for sample size calculation for the study. In an ideal world, we would not like any error in the results of our study; however, we would need to do the study in the entire population (infinite sample size) to be able to get a 0% alpha and beta error. These two errors enable us to do studies with realistic sample sizes, with the compromise that there is a small possibility that the results may not always reflect the truth. The basis for this will be discussed in a subsequent paper in this series dealing with sample size calculation.
Conventionally, type 1 or alpha error is set at 5%. This means, that at the end of the study, if there is a difference between groups, we want to be 95% certain that this is a true difference and allow only a 5% probability that this difference has occurred by chance (false positive). Type 2 or beta error is usually set between 10% and 20%; therefore, the power of the study is 90% or 80%. This means that if there is a difference between groups, we want to be 80% (or 90%) certain that the study will detect that difference. For example, in the ABLE study, sample size was calculated with a type 1 error of 5% (two-sided) and power of 90% (type 2 error of 10%) (1).
Table 1 gives a summary of the two types of statistical errors with an example
Statistical errors
| (a) Types of statistical errors | |||
| : Null hypothesis is | |||
| True | False | ||
| Null hypothesis is actually | True | Correct results! | Falsely rejecting null hypothesis - Type I error |
| False | Falsely accepting null hypothesis - Type II error | Correct results! | |
| (b) Possible statistical errors in the ABLE trial | |||
| There is difference in mortality between groups receiving fresh RBCs and standard-issue RBCs | There difference in mortality between groups receiving fresh RBCs and standard-issue RBCs | ||
| Truth | There is difference in mortality between groups receiving fresh RBCs and standard-issue RBCs | Correct results! | Falsely rejecting null hypothesis - Type I error |
| There difference in mortality between groups receiving fresh RBCs and standard-issue RBCs | Falsely accepting null hypothesis - Type II error | Correct results! | |
In the next article in this series, we will look at the meaning and interpretation of ‘ p ’ value and confidence intervals for hypothesis testing.
Source of support: Nil
Conflict of interest: None

Statistics Made Easy
Bartlett’s Test for Homogeneity of Variances (Definition & Example)
Bartlett’s Test is a statistical test that is used to determine whether or not the variances between several groups are equal.
Many statistical tests (like a one-way ANOVA ) assume that variances are equal across samples. Bartlett’s test can be used to verify that assumption.
The following steps explain how to perform Bartlett’s test.
Note: Don’t confuse this test with Bartlett’s Test of Sphericity , which is used to compare an observed correlation matrix to the identity matrix.
Steps to Perform Bartlett’s Test
Bartlett’s Test uses the following null and alternative hypotheses :
H 0 : The variance among each group is equal.
H A : At least one group has a variance that is not equal to the rest.
The test statistic can be calculated as follows:
B = (n-k)lns 2 – Σ(n j -1)lns j 2 / c
- n: The total number of observations across all groups
- k: The total number of groups
- ln: This stands for “natural log”
- s 2 : The pooled variance
- n j : The number of observations in group j
- s j 2 : The variance of group j
And where c is calculated as:
- c = 1 + (1/3(k-1))*(Σ(1/(n j -1)) – (1/(n-k))
This test statistic follows a Chi-Square distribution with k-1 degrees of freedom. That is, B ~ X 2 (k-1).
If the p-value that corresponds to the test statistic is less than some significance level (like α = 0.05) then we can reject the null hypothesis and conclude that not all groups have the same variance.
Example: Bartlett’s Test
Suppose a professor wants to know if three different studying techniques lead to different average exam scores.
She randomly assigns 10 students to use each technique for one week, then makes each student take an exam of equal difficulty.
The exam scores of the 30 students are shown below:

The professor wants to conduct a one-way ANOVA to see if the three techniques lead to different average exam scores, but she first must conduct Bartlett’s Test to verify that the three groups have equal variances.
It’s cumbersome to perform Bartlett’s Test by hand, so we’ll enter the following data values into the Bartlett’s Test Calculator :

The test returns the following results:
- Test statistic B : 3.30244
- P-value: 0.19182
Since the p-value is not less than 0.05, the professor will fail to reject the null hypothesis. In other words, she doesn’t have sufficient evidence to say that the three groups have different variances.
Thus, she can proceed to perform the one-way ANOVA.
Additional Resources
How to Perform Bartlett’s Test in R (Step-by-Step) How to Perform Bartlett’s Test in Python (Step-by-Step)
Featured Posts
Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike. My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.
Leave a Reply Cancel reply
Your email address will not be published. Required fields are marked *
Join the Statology Community
Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!
By subscribing you accept Statology's Privacy Policy.

- Statistical Reference Guide
- Compare groups
Homogeneity of variance hypothesis test
A homogeneity hypothesis test formally tests if the populations have equal variances.
Many statistical hypothesis tests and estimators of effect size assume that the variances of the populations are equal. This assumption allows the variances of each group to be pooled together to provide a better estimate of the population variance. A better estimate of the variance increases the statistical power of the test meaning you can use a smaller sample size to detect the same difference, or detect smaller differences and make sharper inferences with the same sample size.
- For two samples, the null hypothesis states that the ratio of the variances of the populations is equal to a hypothesized value (usually 1 indicating equality), against the alternative hypothesis that it is not equal to (or less than, or greater than) the hypothesized value.
- For more than two samples, the null hypothesis states that the variances of the populations are equal, against the alternative hypothesis that at least one population variance is different.
When the test p-value is small, you can reject the null hypothesis and conclude that the populations differ in variance.


Snapsolve any problem by taking a picture. Try it in the Numerade app?
9.1 Null and Alternative Hypotheses
The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.
H 0 : The null hypothesis: It is a statement of no difference between the variables—they are not related. This can often be considered the status quo and as a result if you cannot accept the null it requires some action.
H a : The alternative hypothesis: It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 . This is usually what the researcher is trying to prove.
Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.
After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are "reject H 0 " if the sample information favors the alternative hypothesis or "do not reject H 0 " or "decline to reject H 0 " if the sample information is insufficient to reject the null hypothesis.
Mathematical Symbols Used in H 0 and H a :
| equal (=) | not equal (≠) greater than (>) less than (<) |
| greater than or equal to (≥) | less than (<) |
| less than or equal to (≤) | more than (>) |
H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.
Example 9.1
H 0 : No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ .30 H a : More than 30% of the registered voters in Santa Clara County voted in the primary election. p > 30
A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.
Example 9.2
We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are: H 0 : μ = 2.0 H a : μ ≠ 2.0
We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : μ __ 66
- H a : μ __ 66
Example 9.3
We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are: H 0 : μ ≥ 5 H a : μ < 5
We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : μ __ 45
- H a : μ __ 45
Example 9.4
In an issue of U. S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066
On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : p __ 0.40
- H a : p __ 0.40
Collaborative Exercise
Bring to class a newspaper, some news magazines, and some Internet articles . In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.
As an Amazon Associate we earn from qualifying purchases.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/introductory-statistics/pages/1-introduction
- Authors: Barbara Illowsky, Susan Dean
- Publisher/website: OpenStax
- Book title: Introductory Statistics
- Publication date: Sep 19, 2013
- Location: Houston, Texas
- Book URL: https://openstax.org/books/introductory-statistics/pages/1-introduction
- Section URL: https://openstax.org/books/introductory-statistics/pages/9-1-null-and-alternative-hypotheses
© Jun 23, 2022 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.
Chapter 11: Chi-Square Tests
Test of homogeneity, learning objectives.
- Conduct a chi-square test of homogeneity. Interpret the conclusion in context.
We have learned the details for two chi-square tests, the goodness-of-fit test, and the test of independence. Now we focus on the third and last chi-square test that we will learn, the test for homogeneity . This test determines if two or more populations (or subgroups of a population) have the same distribution of a single categorical variable.
The test of homogeneity expands the test for a difference in two population proportions, which is the two-proportion Z-test we learned in Inference for Two Proportions . We use the two-proportion Z-test when the response variable has only two outcome categories and we are comparing two populations (or two subgroups.) We use the test of homogeneity if the response variable has two or more categories and we wish to compare two or more populations (or subgroups.)
We can answer the following research questions with a chi-square test of homogeneity:
- Does the use of steroids in collegiate athletics differ across the three NCAA divisions?
- Was the distribution of political views (liberal, moderate, conservative) different for last three presidential elections in the United States?
The null hypothesis states that the distribution of the categorical variable is the same for the populations (or subgroups). In other words, the proportion with a given response is the same in all of the populations, and this is true for all response categories. The alternative hypothesis says that the distributions differ.
Note: Homogeneous means the same in structure or composition. This test gets its name from the null hypothesis, where we claim that the distribution of the responses are the same (homogeneous) across groups.
To test our hypotheses, we select a random sample from each population and gather data on one categorical variable. As with all chi-square tests, the expected counts reflect the null hypothesis. We must determine what we expect to see in each sample if the distributions are identical. As before, the chi-square test statistic measures the amount that the observed counts in the samples deviate from the expected counts.
Steroid Use in Collegiate Sports
In 2006, the NCAA published a report called “Substance Use: NCAA Study of Substance Use of College Student-Athletes.” We use data from this report to investigate the following question: Does steroid use by student athletes differ for the three NCAA divisions?
The data comes from a random selection of teams in each NCAA division. The sampling plan was somewhat complex, but we can view the data as though it came from a random sample of athletes in each division. The surveys are anonymous to encourage truthful responses.
To see the NCAA report on substance use, click here .
Step 1: State the hypotheses.
In the test of homogeneity, the null hypothesis says that the distribution of a categorical response variable is the same in each population. In this example, the categorical response variable is steroid use (yes or no). The populations are the three NCAA divisions.
- H 0 : The proportion of athletes using steroids is the same in each of the three NCAA divisions.
- H a : The proportion of athletes using steroids is not same in each of the three NCAA divisions.
Note: These hypotheses imply that the proportion of athletes not using steroids is also the same in each of the three NCAA divisions, so we don’t need to state this explicitly. For example, if 2% of the athletes in each division are using steroids, then 98% are not.
Here is an alternative way we could state the hypotheses for a test of homogeneity.
- H 0 : For each of the three NCAA divisions, the distribution of “yes” and “no” responses to the question about steroid use is the same.
- H a : The distribution of responses is not the same.
Step 2: Collect and analyze the data.
We summarized the data from these three samples in a two-way table.

We use percentages to compare the distributions of yes and no responses in the three samples. This step is similar to our data analysis for the test of independence.

We can see that Division I and Division II schools have essentially the same percentage of athletes who admit steroid use (about 1.2%). Not surprisingly, the least competitive division, Division III, has a slightly lower percentage (about 1.0%). Do these results suggest that the proportion of athletes using steroids is the same for the three divisions? Or is the difference seen in the sample of Division III schools large enough to suggest differences in the divisions? After all, the sample sizes are very large. We know that for large samples, a small difference can be statistically significant. Of course, we have to conduct the test of homogeneity to find out.
Note: We decided not to use ribbon charts for visual comparison of the three distributions because the percentage admitting steroid use is too small in each sample to be visible.
Step 3: Assess the evidence.
We need to determine the expected values and the chi-square test statistic so that we can find the P-value.
Calculating Expected Values for a Test of Homogeneity
Expected counts always describe what we expect to see in a sample if the null hypothesis is true. In this situation, we expect the percentage using steroids to be the same for each division. What percentage do we use? We find the percentage using steroids in the combined samples. This calculation is the same as we did when finding expected counts for a test of independence, though the logic of the calculation is subtly different.

Here are the calculations for the response “yes”:
- Percentage using steroids in combined samples: 220/19,377 = 0.01135 = 1.135%
Expected count of steroid users for Division I is 1.135% of Division I sample:
- 0.01135(8,543) = 96.96
Expected count of steroid users for Division II is 1.135% of Division II sample:
- 0.01135(4,341) = 49.27
Expected count of steroid users for Division III is 1.135% of Division III sample:
- 0.01135(6,493) = 73.70
Checking Conditions
The conditions for use of the chi-square distribution are the same as we learned previously:
- A sample is randomly selected from each population.
- All of the expected counts are 5 or greater.
Since this data meets the conditions, we can proceed with calculating the χ 2 test statistic.
Calculating the Chi-Square Test Statistic
There are no changes in the way we calculate the chi-square test statistic.
[latex]{\chi }^{2}\text{}=\text{}∑\frac{{(\mathrm{observed}-\mathrm{expected})}^{2}}{\mathrm{expected}}[/latex]
We use technology to calculate the chi-square value. For this example, we show the calculation. There are six terms, one for each cell in the 3 × 2 table. (We ignore the totals, as always.)

Finding Degrees of Freedom and the P-Value
For chi-square tests based on two-way tables (both the test of independence and the test of homogeneity), the degrees of freedom are ( r − 1)( c − 1), where r is the number of rows and c is the number of columns in the two-way table (not counting row and column totals). In this case, the degrees of freedom are (3 − 1)(2 − 1) = 2.
We use the chi-square distribution with df = 2 to find the P-value. The P-value is large (0.4561), so we fail to reject the null hypothesis.

Step 4: Conclusion.
The data does not provide strong enough evidence to conclude that steroid use differs in the three NCAA divisions (P-value = 0.4561).
Learn By Doing
First use of anabolic steroids by ncaa athletes.
The NCAA survey includes this question: “When, if ever, did you start using anabolic steroids?” The response options are: have never used, before junior high, junior high, high school, freshman year of college, after freshman year of college. We focused on those who admitted use of steroids and compared the distribution of their responses for the years 1997, 2001, and 2005. (These are the years that the NCAA conducted the survey. Counts are estimates from reported percentages and sample size.) Recall that the NCAA uses random sampling in its sampling design.

Please click here to open the simulation for use in the following activity.
We now know the details for the chi-square test for homogeneity. We conclude with two activities that will give you practice recognizing when to use this test.
Gender and Politics
Consider these two situations:
- A: Liberal, moderate, or conservative: Are there differences in political views of men and women in the United States? We survey a random sample of 100 U.S. men and 100 U.S. women.
- B: Do you plan to vote in the next presidential election? We ask a random sample of 100 U.S. men and 100 U.S. women. We look for differences in the proportion of men and women planning to vote.
Steroid Use for Male Athletes in NCAA Sports
We plan to compare steroid use for male athletes in NCAA baseball, basketball, and football. We design two different sampling plans.
- A: Survey distinct random samples of NCAA athletes from each sport: 500 baseball players, 400 basketball players, 900 football players.
- B. Survey a random sample of 1,800 NCAA male athletes and categorize players by sport and admitted steroid use. Responses are anonymous.
Let’s Summarize
In “Chi-Square Tests for Two-Way Tables,” we discussed two different hypothesis tests using the chi-square test statistic:
- Test of independence for a two-way table
- Test of homogeneity for a two-way table
Test of Independence for a Two-Way Table
- In the test of independence, we consider one population and two categorical variables.
- In Probability and Probability Distribution , we learned that two events are independent if P ( A | B ) = P ( A ), but we did not pay attention to variability in the sample. With the chi-square test of independence, we have a method for deciding whether our observed P ( A | B ) is “too far” from our observed P ( A ) to infer independence in the population.
- The null hypothesis says the two variables are independent (or not associated). The alternative hypothesis says the two variables are dependent (or associated).
- To test our hypotheses, we select a single random sample and gather data for two different categorical variables.
- Example: Do men and women differ in their perception of their weight? Select a random sample of adults. Ask them two questions: (1) Are you male or female? (2) Do you feel that you are overweight, underweight, or about right in weight?
Test of Homogeneity for a Two-Way Table
- In the test of homogeneity, we consider two or more populations (or two or more subgroups of a population) and a single categorical variable.
- The test of homogeneity expands on the test for a difference in two population proportions that we learned in Inference for Two Proportions by comparing the distribution of the categorical variable across multiple groups or populations.
- The null hypothesis says that the distribution of proportions for all categories is the same in each group or population. The alternative hypothesis says that the distributions differ.
- To test our hypotheses, we select a random sample from each population or subgroup independently. We gather data for one categorical variable.
- Example: Is the rate of steroid use different for different men’s collegiate sports (baseball, basketball, football, tennis, track/field)? Randomly select a sample of athletes from each sport and ask them anonymously if they use steroids.
The difference between these two tests is subtle. They differ primarily in study design. In the test of independence, we select individuals at random from a population and record data for two categorical variables. The null hypothesis says that the variables are independent. In the test of homogeneity, we select random samples from each subgroup or population separately and collect data on a single categorical variable. The null hypothesis says that the distribution of the categorical variable is the same for each subgroup or population.
Both tests use the same chi-square test statistic.
The Chi-Square Test Statistic and Distribution
For all chi-square tests, the chi-square test statistic χ 2 is the same. It measures how far the observed data are from the null hypothesis by comparing observed counts and expected counts. Expected counts are the counts we expect to see if the null hypothesis is true.
The chi-square model is a family of curves that depend on degrees of freedom. For a two-way table, the degrees of freedom equals ( r − 1)( c − 1). All chi-square curves are skewed to the right with a mean equal to the degrees of freedom.
A chi-square model is a good fit for the distribution of the chi-square test statistic only if the following conditions are met:
- The sample is randomly selected.
- All expected counts are 5 or greater.
If these conditions are met, we use the chi-square distribution to find the P-value. We use the same logic that we have used in all hypothesis tests to draw a conclusion based on the P-value. If the P-value is at least as small as the significance level, we reject the null hypothesis and accept the alternative hypothesis. The P-value is the likelihood that results from random samples have a χ 2 value equal to or greater than that calculated from the data if the null hypothesis is true.
- Concepts in Statistics. Provided by : Open Learning Initiative. Located at : http://oli.cmu.edu . License : CC BY: Attribution

Privacy Policy
Journal of Materials Chemistry A
Copper- and manganese-based layered hybrid organic–inorganic compounds with polymorphic transitions as energy storage materials †.
* Corresponding authors
a Department of Materials Science and Physical Chemistry, Section of Materials Science and Engineering, Faculty of Chemistry, Universitat de Barcelona, C/ Martí i Franquès 1-11, Barcelona, Spain E-mail: [email protected]
b X-ray Diffraction Unit, Scientific and Technological Centers, University of Barcelona, Lluís Solé i Sabarís 1-3, Barcelona, Spain
c Department of Inorganic and Organic Chemistry, Section of Organic Chemistry, Faculty of Chemistry, Universitat de Barcelona, C/ Martí i Franquès 1-11, 08028 Barcelona, Spain
Solid–solid phase change materials (ss-PCM) have emerged as a promising alternative to traditional methods of thermal regulation, such as solid–liquid transformations. Due to their wide operational temperature range and competitive performance, ss-PCM materials are increasingly being explored for their potential in cooling electronic devices. Here, we explore the potential of layered hybrid organic–inorganic perovskites (LHOIPs) as thermal energy storage materials for passive cooling applications. Two formulations, bis(dodecylammonium) tetrachlorocuprate( II ) (CuC 12 ) and bis(dodecylammonium) tetrachloromanganate( II ) (MnC 12 ) were synthesised and comprehensively characterised. The analyses revealed that these materials present a two-dimensional structure with a triclinic conformation at 100 K. Notably, both materials exhibited a polymorphic transformation with low thermal hysteresis (1.3–2.5 K). These findings indicate that these materials hold significant potential as thermoregulator materials in cooling electronics. Furthermore, both CuC 12 and MnC 12 demonstrated good thermal stability compared to other types of ss-PCM. Overall, the findings of this study suggest that LHOIPs, particularly CuC 12 and MnC 12 , are promising candidates for further exploration as thermal energy storage materials in electronic cooling applications.

Supplementary files
- Supplementary information PDF (498K)
- Crystal structure data CIF (2773K)
Article information
Download Citation
Permissions.
Copper- and manganese-based layered hybrid organic–inorganic compounds with polymorphic transitions as energy storage materials
R. Salgado-Pizarro, C. Puigjaner, J. García, A. I. Fernández and C. Barreneche, J. Mater. Chem. A , 2024, Advance Article , DOI: 10.1039/D4TA01060D
This article is licensed under a Creative Commons Attribution-NonCommercial 3.0 Unported Licence . You can use material from this article in other publications, without requesting further permission from the RSC, provided that the correct acknowledgement is given and it is not used for commercial purposes.
To request permission to reproduce material from this article in a commercial publication , please go to the Copyright Clearance Center request page .
If you are an author contributing to an RSC publication, you do not need to request permission provided correct acknowledgement is given.
If you are the author of this article, you do not need to request permission to reproduce figures and diagrams provided correct acknowledgement is given. If you want to reproduce the whole article in a third-party commercial publication (excluding your thesis/dissertation for which permission is not required) please go to the Copyright Clearance Center request page .
Read more about how to correctly acknowledge RSC content .
Social activity
Search articles by author.
This article has not yet been cited.
Advertisements

IMAGES
VIDEO
COMMENTS
The alternative hypothesis is then: \(\mathbf{H_A:}\) The population distributions of the responses for variable \(\mathbf{y}\) are NOT ALL the same across the \(\mathbf{R}\) groups. To make this concrete, consider what the proportions could look like if they satisfied the null hypothesis for the Arthritis example, as displayed in Figure 5.4 ...
The null hypothesis says that the variables are independent. In the test of homogeneity, we select random samples from each subgroup or population separately and collect data on a single categorical variable. The null hypothesis says that the distribution of the categorical variable is the same for each subgroup or population.
State the null and alternative hypotheses, the degrees of freedom and the test statistic, sketch the graph of the p-value, and draw a conclusion about the test of homogeneity. Answer \(H_{0}\): The distribution of regular applications accepted is the same as the distribution of early applications accepted.
State the null and alternative hypotheses, the degrees of freedom and the test statistic, sketch the graph of the p-value, and draw a conclusion about the test of homogeneity. H 0 : The distribution of regular applications accepted is the same as the distribution of early applications accepted.
9.1 Null and Alternative Hypotheses; 9.2 Outcomes and the Type I and Type II Errors; 9.3 Distribution Needed for Hypothesis Testing; 9.4 Rare Events, the Sample, and the Decision and Conclusion; ... suffice to decide whether two populations follow the same unknown distribution. A different test, called the test for homogeneity, can be used to ...
The null hypothesis says that the variables are independent. In the test of homogeneity, we select random samples from each subgroup or population separately and collect data on a single categorical variable. The null hypothesis says that the distribution of the categorical variable is the same for each subgroup or population.
The null hypothesis (H 0) answers "No, there's no effect in the population." The alternative hypothesis (H a) answers "Yes, there is an effect in the population." The null and alternative are always claims about the population. That's because the goal of hypothesis testing is to make inferences about a population based on a sample.
The actual test begins by considering two hypotheses.They are called the null hypothesis and the alternative hypothesis.These hypotheses contain opposing viewpoints. H 0, the —null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.
17.1 - Test For Homogeneity. As suggested in the introduction to this lesson, the test for homogeneity is a method, based on the chi-square statistic, for testing whether two or more multinomial distributions are equal. Let's start by trying to get a feel for how our data might "look" if we have two equal multinomial distributions.
Alternative hypothesis: At least one of the null hypothesis statements is false. Formulate an analysis plan. For this analysis, the significance level is 0.05. Using sample data, we will conduct a chi-square test for homogeneity. Analyze sample data. Applying the chi-square test for homogeneity to sample data, we compute the degrees of freedom ...
These institutions do not offer athletic scholarships. Step 1: State the hypotheses. In the test of homogeneity, the null hypothesis says that the distribution of a categorical response variable is the same in each population. In this example, the categorical response variable is steroid use (yes or no). The populations are the three NCAA ...
Step 1: State the hypotheses. In the test of homogeneity, the null hypothesis says that the distribution of a categorical response variable is the same in each population. In this example, the categorical response variable is steroid use (yes or no). The populations are the three NCAA divisions. H 0: The proportion of athletes using steroids is ...
State the null and alternative hypotheses, the degrees of freedom and the test statistic, sketch the graph of the p-value, and draw a conclusion about the test of homogeneity. Solution H 0 : The distribution of regular applications accepted is the same as the distribution of early applications accepted.
The null hypothesis and the alternative hypothesis are types of conjectures used in statistical tests to make statistical inferences, ... Null hypotheses of homogeneity are used to verify that multiple experiments are producing consistent results. For example, the effect of a medication on the elderly is consistent with that of the general ...
The actual test begins by considering two hypotheses.They are called the null hypothesis and the alternative hypothesis.These hypotheses contain opposing viewpoints. \(H_0\): The null hypothesis: It is a statement of no difference between the variables—they are not related. This can often be considered the status quo and as a result if you cannot accept the null it requires some action.
HYPOTHESIS TESTING. A clinical trial begins with an assumption or belief, and then proceeds to either prove or disprove this assumption. In statistical terms, this belief or assumption is known as a hypothesis. Counterintuitively, what the researcher believes in (or is trying to prove) is called the "alternate" hypothesis, and the opposite ...
Bartlett's Test uses the following null and alternative hypotheses: H 0: The variance among each group is equal. H A: At least one group has a variance that is not equal to the rest. The test statistic can be calculated as follows: B = (n-k)lns 2 - Σ(n j-1)lns j 2 / c. where: n: The total number of observations across all groups; k: The ...
The actual test begins by considering two hypotheses.They are called the null hypothesis and the alternative hypothesis.These hypotheses contain opposing viewpoints. H 0: The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt.
A homogeneity hypothesis test formally tests if the populations have equal variances. ... the null hypothesis states that the ratio of the variances of the populations is equal to a hypothesized value (usually 1 indicating equality), against the alternative hypothesis that it is not equal to (or less than, or greater than) the hypothesized ...
The alternative hypothesis is a statement that the observed difference in data is due to a relationship in the population and not due to chance alone. Step 2/4 Step 2: For a chi-square homogeneity test, the null hypothesis and alternative hypothesis are defined in terms of the distribution of a designated variable across different populations ...
The actual test begins by considering two hypotheses.They are called the null hypothesis and the alternative hypothesis.These hypotheses contain opposing viewpoints. H 0: The null hypothesis: It is a statement of no difference between the variables—they are not related. This can often be considered the status quo and as a result if you cannot accept the null it requires some action.
The null hypothesis says that the variables are independent. In the test of homogeneity, we select random samples from each subgroup or population separately and collect data on a single categorical variable. The null hypothesis says that the distribution of the categorical variable is the same for each subgroup or population.
Solid-solid phase change materials (ss-PCM) have emerged as a promising alternative to traditional methods of thermal regulation, such as solid-liquid transformations. Due to their wide operational temperature range and competitive performance, ss-PCM materials are increasingly being explored for their potential in