Quadratic assignment problem
Author: Thomas Kueny, Eric Miller, Natasha Rice, Joseph Szczerba, David Wittmann (SysEn 5800 Fall 2020)
- 1 Introduction
- 2.1 Koopmans-Beckman Mathematical Formulation
- 2.2.1 Parameters
- 2.3.1 Optimization Problem
- 2.4 Computational Complexity
- 2.5 Algorithmic Discussions
- 2.6 Branch and Bound Procedures
- 2.7 Linearizations
- 3.1 QAP with 3 Facilities
- 4.1 Inter-plant Transportation Problem
- 4.2 The Backboard Wiring Problem
- 4.3 Hospital Layout
- 4.4 Exam Scheduling System
- 5 Conclusion
- 6 References

Introduction
The Quadratic Assignment Problem (QAP), discovered by Koopmans and Beckmann in 1957 [1] , is a mathematical optimization module created to describe the location of invisible economic activities. An NP-Complete problem, this model can be applied to many other optimization problems outside of the field of economics. It has been used to optimize backboards, inter-plant transportation, hospital transportation, exam scheduling, along with many other applications not described within this page.
Theory, Methodology, and/or Algorithmic Discussions
Koopmans-beckman mathematical formulation.
Economists Koopmans and Beckman began their investigation of the QAP to ascertain the optimal method of locating important economic resources in a given area. The Koopmans-Beckman formulation of the QAP aims to achieve the objective of assigning facilities to locations in order to minimize the overall cost. Below is the Koopmans-Beckman formulation of the QAP as described by neos-guide.org.
Quadratic Assignment Problem Formulation

Inner Product

Note: The true objective cost function only requires summing entries above the diagonal in the matrix comprised of elements

Since this matrix is symmetric with zeroes on the diagonal, dividing by 2 removes the double count of each element to give the correct cost value. See the Numerical Example section for an example of this note.
Optimization Problem
With all of this information, the QAP can be summarized as:

Computational Complexity
QAP belongs to the classification of problems known as NP-complete, thus being a computationally complex problem. QAP’s NP-completeness was proven by Sahni and Gonzalez in 1976, who states that of all combinatorial optimization problems, QAP is the “hardest of the hard”. [2]
Algorithmic Discussions
While an algorithm that can solve QAP in polynomial time is unlikely to exist, there are three primary methods for acquiring the optimal solution to a QAP problem:
- Dynamic Program
- Cutting Plane
Branch and Bound Procedures
The third method has been proven to be the most effective in solving QAP, although when n > 15, QAP begins to become virtually unsolvable.
The Branch and Bound method was first proposed by Ailsa Land and Alison Doig in 1960 and is the most commonly used tool for solving NP-hard optimization problems.
A branch-and-bound algorithm consists of a systematic enumeration of candidate solutions by means of state space search: the set of candidate solutions is thought of as forming a rooted tree with the full set at the root. The algorithm explores branches of this tree, which represent subsets of the solution set. Before one lists all of the candidate solutions of a branch, the branch is checked against upper and lower estimated bounds on the optimal solution, and the branch is eliminated if it cannot produce a better solution than the best one found so far by the algorithm.
Linearizations
The first attempts to solve the QAP eliminated the quadratic term in the objective function of

in order to transform the problem into a (mixed) 0-1 linear program. The objective function is usually linearized by introducing new variables and new linear (and binary) constraints. Then existing methods for (mixed) linear integer programming (MILP) can be applied. The very large number of new variables and constraints, however, usually poses an obstacle for efficiently solving the resulting linear integer programs. MILP formulations provide LP relaxations of the problem which can be used to compute lower bounds.
Numerical Example
Qap with 3 facilities.

| Permutation | Cost |
| (123) | 91.4 |
| 99.8 | |
| 98.4 | |
| 86.5 | |
| 103.3 | |
| 90 |

Applications
Inter-plant transportation problem.
The QAP was first introduced by Koopmans and Beckmann to address how economic decisions could be made to optimize the transportation costs of goods between both manufacturing plants and locations. [1] Factoring in the location of each of the manufacturing plants as well as the volume of goods between locations to maximize revenue is what distinguishes this from other linear programming assignment problems like the Knapsack Problem.
The Backboard Wiring Problem
As the QAP is focused on minimizing the cost of traveling from one location to another, it is an ideal approach to determining the placement of components in many modern electronics. Leon Steinberg proposed a QAP solution to optimize the layout of elements on a blackboard by minimizing the total amount of wiring required. [4]
When defining the problem Steinberg states that we have a set of n elements

as well as a set of r points

In his paper he derives the below formula:

In his paper Steinberg a backboard with a 9 by 4 array, allowing for 36 potential positions for the 34 components that needed to be placed on the backboard. For the calculation, he selected a random initial placement of s1 and chose a random family of 25 unconnected sets.
The initial placement of components is shown below:

After the initial placement of elements, it took an additional 35 iterations to get us to our final optimized backboard layout. Leading to a total of 59 iterations and a final wire length of 4,969.440.
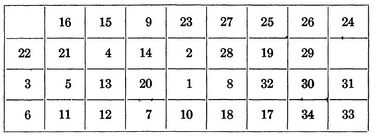
Hospital Layout
Building new hospitals was a common event in 1977 when Alealid N Elshafei wrote his paper on "Hospital Layouts as a Quadratic Assignment Problem". [5] With the high initial cost to construct the hospital and to staff it, it is important to ensure that it is operating as efficiently as possible. Elshafei's paper was commissioned to create an optimization formula to locate clinics within a building in such a way that minimizes the total distance that a patient travels within the hospital throughout the year. When doing a study of a major hospital in Cairo he determined that the Outpatient ward was acting as a bottleneck in the hospital and focused his efforts on optimizing the 17 departments there.
Elshafei identified the following QAP to determine where clinics should be placed:

For the Cairo hospital with 17 clinics, and one receiving and recording room bringing us to a total of 18 facilities. By running the above optimization Elshafei was able to get the total distance per year down to 11,281,887 from a distance of 13,973,298 based on the original hospital layout.
Exam Scheduling System
The scheduling system uses matrices for Exams, Time Slots, and Rooms with the goal of reducing the rate of schedule conflicts. To accomplish this goal, the “examination with the highest cross faculty student is been prioritized in the schedule after which the examination with the highest number of cross-program is considered and finally with the highest number of repeating student, at each stage group with the highest number of student are prioritized.” [6]

- ↑ 1.0 1.1 1.2 Koopmans, T., & Beckmann, M. (1957). Assignment Problems and the Location of Economic Activities. Econometrica, 25(1), 53-76. doi:10.2307/1907742
- ↑ 2.0 2.1 Quadratic Assignment Problem. (2020). Retrieved December 14, 2020, from https://neos-guide.org/content/quadratic-assignment-problem
- ↑ 3.0 3.1 3.2 Burkard, R. E., Çela, E., Pardalos, P. M., & Pitsoulis, L. S. (2013). The Quadratic Assignment Problem. https://www.opt.math.tugraz.at/~cela/papers/qap_bericht.pdf .
- ↑ 4.0 4.1 Leon Steinberg. The Backboard Wiring Problem: A Placement Algorithm. SIAM Review . 1961;3(1):37.
- ↑ 5.0 5.1 Alwalid N. Elshafei. Hospital Layout as a Quadratic Assignment Problem. Operational Research Quarterly (1970-1977) . 1977;28(1):167. doi:10.2307/300878
- ↑ 6.0 6.1 Muktar, D., & Ahmad, Z.M. (2014). Examination Scheduling System Based On Quadratic Assignment.
Navigation menu
- Analysis of Algorithms
- Backtracking
- Dynamic Programming
- Divide and Conquer
- Geometric Algorithms
- Mathematical Algorithms
- Pattern Searching
- Bitwise Algorithms
- Branch & Bound
- Randomized Algorithms
Quadratic Assignment Problem (QAP)
- Channel Assignment Problem
- Assignment Operators In C++
- Solidity - Assignment Operators
- Job Assignment Problem using Branch And Bound
- Worker-Bike Assignments (Campus Bikes)
- Range Minimum Query with Range Assignment
- Transportation Problem | Set 1 (Introduction)
- Transportation Problem | Set 2 (NorthWest Corner Method)
- Transportation Problem | Set 3 (Least Cost Cell Method)
- Transportation Problem | Set 4 (Vogel's Approximation Method)
- Minimum boats to save people
- Assignment Operators in C
- QA - Placement Quizzes | Profit and Loss | Question 7
- QA - Placement Quizzes | Profit and Loss | Question 4
- QA - Placement Quizzes | Profit and Loss | Question 12
- QA - Placement Quizzes | Profit and Loss | Question 10
- QA - Placement Quizzes | Age | Question 4
- IBM Placement Paper | Quantitative Analysis Set - 5
- IBM Placement Paper | Quantitative Analysis Set - 4
The Quadratic Assignment Problem (QAP) is an optimization problem that deals with assigning a set of facilities to a set of locations, considering the pairwise distances and flows between them.
The problem is to find the assignment that minimizes the total cost or distance, taking into account both the distances and the flows.
The distance matrix and flow matrix, as well as restrictions to ensure each facility is assigned to exactly one location and each location is assigned to exactly one facility, can be used to formulate the QAP as a quadratic objective function.
The QAP is a well-known example of an NP-hard problem , which means that for larger cases, computing the best solution might be difficult. As a result, many algorithms and heuristics have been created to quickly identify approximations of answers.
There are various types of algorithms for different problem structures, such as:
- Precise algorithms
- Approximation algorithms
- Metaheuristics like genetic algorithms and simulated annealing
- Specialized algorithms
Example: Given four facilities (F1, F2, F3, F4) and four locations (L1, L2, L3, L4). We have a cost matrix that represents the pairwise distances or costs between facilities. Additionally, we have a flow matrix that represents the interaction or flow between locations. Find the assignment that minimizes the total cost based on the interactions between facilities and locations. Each facility must be assigned to exactly one location, and each location can only accommodate one facility.
Facilities cost matrix:
| L1 | L2 | L3 | L4 | |
|---|---|---|---|---|
| F1 | 0 | 2 | 3 | 1 |
| F2 | 2 | 0 | 1 | 4 |
| F3 | 3 | 1 | 0 | 2 |
| F4 | 1 | 4 | 2 | 0 |
Flow matrix:
| F1 | F2 | F3 | F4 | |
|---|---|---|---|---|
| L1 | 0 | 1 | 2 | 3 |
| L2 | 1 | 0 | 4 | 2 |
| L3 | 2 | 4 | 0 | 1 |
| L4 | 3 | 2 | 1 | 0 |
To solve the QAP, various optimization techniques can be used, such as mathematical programming, heuristics, or metaheuristics. These techniques aim to explore the search space and find the optimal or near-optimal solution.
The solution to the QAP will provide an assignment of facilities to locations that minimizes the overall cost.
The solution generates all possible permutations of the assignment and calculates the total cost for each assignment. The optimal assignment is the one that results in the minimum total cost.
To calculate the total cost, we look at each pair of facilities in (i, j) and their respective locations (location1, location2). We then multiply the cost of assigning facility1 to facility2 (facilities[facility1][facility2]) with the flow from location1 to location2 (locations[location1][location2]). This process is done for all pairs of facilities in the assignment, and the costs are summed up.
Overall, the output tells us that assigning facilities to locations as F1->L1, F3->L2, F2->L3, and F4->L4 results in the minimum total cost of 44. This means that Facility 1 is assigned to Location 1, Facility 3 is assigned to Location 2, Facility 2 is assigned to Location 3, and Facility 4 is assigned to Location 4, yielding the lowest cost based on the given cost and flow matrices.This example demonstrates the process of finding the optimal assignment by considering the costs and flows associated with each facility and location. The objective is to find the assignment that minimizes the total cost, taking into account the interactions between facilities and locations.
Applications of the QAP include facility location, logistics, scheduling, and network architecture, all of which require effective resource allocation and arrangement.
Please Login to comment...
Similar reads, improve your coding skills with practice.
What kind of Experience do you want to share?
(Stanford users can avoid this Captcha by logging in.)
- Send to text email RefWorks EndNote printer
The Quadratic Assignment Problem : Theory and Algorithms
Available online.
- SpringerLink
More options
- Find it at other libraries via WorldCat
- Contributors
Description
Creators/contributors, contents/summary.
- Preface. List of Figures. List of Tables.
- 1. Problem Statement and Complexity Aspects.
- 2. Exact Algorithms and Lower Bounds.
- 3. Heuristics and Asymptotic Behavior.
- 4. QAPs on Specially Structured Matrices.
- 5. Two More Restricted Versions of the QAP.
- 6. QAPs Arising as Optimization Problems in Graphs.
- 7. On the Biquadratic Assignment Problem (BIQAP). References. Notation Index. Subject Index.
- (source: Nielsen Book Data)
Bibliographic information
- Stanford Home
- Maps & Directions
- Search Stanford
- Emergency Info
- Terms of Use
- Non-Discrimination
- Accessibility
© Stanford University , Stanford , California 94305 .

The week's pick

Random Articles
- Configuration Issues and Efforts for Configuring Agile Approaches-Situational based Method Engineering January 2013 Personalization of Web Browsing for Novice Users February 2010 Ontology based Web Page Topic Identification January 2014 A Design of Star Shaped Fractal Antenna for Wireless Applications January 2016
Reseach Article
A survey of quadratic assignment problems.

| International Journal of Computer Applications |
| Foundation of Computer Science (FCS), NY, USA |
| Volume 101 - Number 6 |
| Year of Publication: 2014 |
| Authors: Abdel Nasser H. Zaied, Laila Abd El-fatah Shawky |
Abdel Nasser H. Zaied, Laila Abd El-fatah Shawky . A Survey of Quadratic Assignment Problems. International Journal of Computer Applications. 101, 6 ( September 2014), 28-36. DOI=10.5120/17693-8662
The quadratic assignment problem (QAP) is very challengeable and interesting problem that can model many real-life problems. In this paper, we will simply discuss the meaning of quadratic assignment problem, solving techniques and we will give a survey of some developments and researches.
- E. M. Loiola, N. M. de Abreu, P. O. Boaventura-Netto, P. Hahn, T. Querido. A survey for the quadratic assignment problem. European journal of operational research, 27 December 2005.
- Quadratic Assignment Problem. (2012). retrieved May 2014 , from: http://www. neos-guide. org/content/quadratic-assignment-problem
- QAPLIB - A Quadratic Assignment Problem Library. (2012). Retrieved May 2014, from: http://www. seas. upenn. edu/qaplib
- P. Ji, Y. Wu, H. Liu. A Solution Method for the Quadratic Assignment Problem (QAP), Department of Industrial and Systems Engineering, The Hong Kong Polytechnic University, Hung Hom, Kowloon, Hong Kong ,China, August 2006.
- Quadratic assignment problem. (2013). Retrieved May 2014, from: http://en. wikipedia. org/wiki/Quadratic_assignment_problem
- I. Kudelska . Methods of using the quadratic assignment problem solution, LogForum 8, Issue 3, 2012.
- Assignment problem (2014). Retrieved May 2014, from: http://en. wikipedia. org/wiki/Assignment_problem
- T. Stützle. Iterated local search for the quadratic assignment problem, European Journal of Operational Research , Volume 174, Issue 3, 1 November 2006.
- Z. Wu, Y. Yang, F. Bai, J. Tian. Global optimality conditions and optimization methods for quadratic assignment problems , Volume 218, Issue 11, 5 February 2012.
- E. Duman, M. Uysal, A. F. Alkaya. Migrating Birds Optimization: A new metaheuristic approach and its performance on quadratic assignment problem, Information Sciences, Volume 217, 25 December 2012.
- U. Benlic, J. Hao. Breakout local search for the quadratic assignment problem, Applied Mathematics and Computation, Volume 219, Issue 9, 1 January 2013.
- E. . Klerk, M. Nagy, R. Sotirov, U. Truetsch. Symmetry in RLT-type relaxations for the quadratic assignment and standard quadratic optimization problems, European Journal of Operational Research, Volume 233, Issue 3, 16 March 2014.
- Y. Xia, and Y. Yuan. A new linearization method for quadratic assignment problems, Institute of Computational Mathematics and Scientific/Engineering Computing,The Academy of Mathematics and Systems Sciences,Chinese Academy of Sciences, Beijing, China.
- R. E. Burkard , E. Cela ,P. M. Pardalos , and L. S. Pitsoulis. The Quadratic Assignment Problem, Handbook of combinatorial optimization, 1998.
- C. W. Commander. A Survey of the Quadratic Assignment Problem, with Applications, Morehead Electronic Journal of Applicable Mathematics, Issue 4,1 March 2005.
- N. W. Brixius and K. M. Anstreicher. The Steinberg wiring problem. Working Paper, The University of Iowa, October 2001.
- A. N. Elshafei. Hospital layout as a quadratic assignment problem, Operational Research Quarterly, 1977.
- Juillet. comparison of iterative searches for the quadratic assignment problem, Montréal university, Canada,1994.
- E. M. Loiola, N. M. de Abreu, P. O. Boaventura-Netto, P. Hahn, and T. Querido. A survey for the quadratic assignment problem, European Journal of Operational Research, 27 December 2005.
- F. D. Fomeni. New Solution Approaches for the Quadratic Assignment Problem, University of the Witwatersrand, Johannesburg, September 2011.
- R. K. Ahuja, K. C. Jha, J. B. Orlin and D. Sharma. Very large-scale neighborhood search for the quadratic assignment problem, Working Paper, MIT Sloan School of Management, July 2002.
- N. Christofides and E. Benavent. An exact algorithm for the quadratic assignment problem on a tree, Operation Research, 1989.
- E. -G. Talbi , O. Roux, C. Fonlupt, and D. Robillard. Parallel Ant Colonies for the quadratic assignment problem. Future Generation Computer Systems , Volume 17 ,France, 2001.
- M. Dorigo. Optimization, learning and natural algorithms, Ph. D. Thesis, Politecnico di Milano, Italy, 1992.
- A. kaveh. Algorithms and theoretical topics on selected combinatorial optimization problems. Simon fraser university,2006.
- T. C. Koopmans and M. Beckman. Assignment Problems and the Location of Economic Activities. Econometric ,1957.
- Hanan, M. and J. M. Kurtzberg . A Review of the Placement and Quadratic Assignment Problems, 1972.
- Sahni, S. and T. Gonzalez. P-Complete Aproximation Problems. Journal of the ACM ,1976.
- P. C. Gilmore . Optimal and Suboptimal Algorithms for the Quadratic Assignment Problem. SIAM Journal on Applied Mathematics , Volume 10, 1962.
- E. L. Lawler. The Quadratic Assignment Problem, Management Science, Volume 9, 1963.
- M. S. Hussin and T. Stutzle. Hierarchical Iterated Local Search for the Quadratic Assignment Problem, Institut de Recherches Interdisciplinaires, et de D´eveloppements en Intelligence Artificielle, Universite Libre de Bruxelles, Bruxelles, Belgium, June 2009.
- F. Rendl and H. Wolkowicz . Applications of Parametric Programming and Eigenvalue Maximization to the Quadratic Assignment Problem. Mathematical Programming , Volume 53, 1992.
- P. . M. Zvidrezner , and E. D. Taillard. Recent Advances for the Quadratic Assignment Problem with Special Emphasis on Instances that are Difficult for Meta-Heuristic Methods. Annals of Operations Research , Volume 139, 2005.
- P. Carraresi, and F. Malucelli. A New Lower Bound for the Quadratic Assignment Problem. Tech Report TR-34/92, Universita di Pisa, 1992.
- M. Dell'Amico, J. Carlos D´?az , M. Iori and R. Montanari . The single-finger keyboard layout problem. University of Modena and Reggio Emilia, Italy, November 2008.
- P. M. Pardalos, F. Rendl, and H. Wolkowicz. The Quadratic Assignment Problem: A Survey and Recent Developments, in Quadratic Assignment and Related Problems, DIMACS Series in Discrete Mathematics and Theoretical Computer Science, Volume 16, 1994.
- P. Hahn, T. Grant, and N. Hall. A Branch-and-Bound Algorithm for the Quadratic Assignment Problem Based on the Hungarian Method, European Journal of Operational Research, 1996.
- M. S. Bazaraa and H. D. Sherali. On the Use of Exact and Heuristic Cutting Plane Methods for the Quadratic Assignment Problem . The Journal of the Operational Research Society, Volume 33, Issue 11, Novmber 1982.
- G. Erdo?an. quadratic assignment problem:linearizations and polynomial time solvable cases. October, 2006.
- R. Bellman, An introduction to the theory of dynamic programming, 1953.
- Francesco. A Bandit-Inspired Memetic Algorithm for Quadratic Assignment Problems. University of Utrecht. August 2012.
- E. Cela. Assignment Problems . Technical University Graz, Institute of Mathematics,Steyrergasse 30, A-8010 Graz, Austria.
- G. C. Armour, and E. S. Buffa. Heuristic Algorithm and Simulation Approach to Relative Location of Facilities. Management Science, Volume 9, 1963.
- Y. Li, P. M. Pardalos, and M. G. C. Resende. A Greedy Randomized Adaptive Search Procedure for the Quadratic Assignment Problem. DIMACS Series in Discrete Mathematics and Theoretical Computer Science.
- B. Vahedinori, M. Kianpour and P. Fattahi. Using Greedy Randomize Adaptive Search Procedure for solve the Quadratic Assignment Problem, Volume 22, November 2011.
- H. M. Nehi, and S. Gelareh. A Survey of Meta-Heuristic Solution Methods for the Quadratic Assignment Problem. Applied Mathematical Sciences, Volume 1, Issue 46, 2007.
Index Terms
Computer Science Information Sciences
Quadratic Assignment Problem formulation Exact Algorithm NP-complete Bound Heuristic.
The Quadratic Assignment Problem
- pp 1713–1809
Cite this chapter

- Rainer E. Burkard 3 ,
- Eranda Çela 3 ,
- Panos M. Pardalos 4 &
- Leonidas S. Pitsoulis 4
4470 Accesses
80 Citations
The quadratic assignment problem (QAP) was introduced by Koopmans and Beckmann in 1957 as a mathematical model for the location of a set of indivisible economical activities [113]. Consider the problem of allocating a set of facilities to a set of locations, with the cost being a function of the distance and flow between the facilities, plus costs associated with a facility being placed at a certain location. The objective is to assign each facility to a location such that the total cost is minimized. Specifically, we are given three n x n input matrices with real elements F = ( f ij ), D = ( d kl ) and B = ( b ik ), where f ij is the flow between the facility i and facility j , d kl is the distance between the location k and location l , and b ik is the cost of placing facility i at location k . The Koopmans-Beckmann version of the QAP can be formulated as follows: Let n be the number of facilities and locations and denote by N the set N = {1, 2,..., n}.
These authors have been supported by the Spezialforschungsbereich F 003 “Optimierung und Kontrolle”, Projektbereich Diskrete Optimierung.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
- Available as PDF
- Read on any device
- Instant download
- Own it forever
- Compact, lightweight edition
- Dispatched in 3 to 5 business days
- Free shipping worldwide - see info
- Durable hardcover edition
Tax calculation will be finalised at checkout
Purchases are for personal use only
Institutional subscriptions
Unable to display preview. Download preview PDF.
Similar content being viewed by others

Quadratic Assignment Problems
A linear formulation with $$o(n^2)$$ variables for quadratic assignment problems with manhattan distance matrices.
E. H. L. Aarts and J. Korst, Simulated Annealing and Boltzmann Machines: A Stochastic Approach to Combinatorial Optimization and Neural Computing , Wiley, Chichester, 1989.
MATH Google Scholar
E. Aarts and J. K. Lenstra, eds., Local Search in Combinatorial Optimization , Wiley, Chichester, 1997.
W. P. Adams and T. A. Johnson, Improved linear programming-based lower bounds for the quadratic assignment problem, in Quadratic Assignment and Related Problems , P. M. Pardalos and H. Wolkowicz, eds., DIMACS Series on Discrete Mathematics and Theoretical Computer Science 16 , 1994, 43–75, AMS, Providence, RI.
Google Scholar
W. P. Adams and H. D. Sherali, A tight linearization and an algorithm for zero-one quadratic programming problems, Management Science 32 , 1986, 1274–1290.
Article MATH MathSciNet Google Scholar
W. P. Adams and H. D. Sherali, Linearization strategies for a class of zero-one mixed integer programming problems, Operations Research 38 , 1990, 217–226.
R. K. Ahuja, J. B. Orlin, and A. Tivari, A greedy genetic algorithm for the quadratic assignment problem, Working paper 3826–95, Sloan School of Management, MIT, 1995.
S. Arora, A. Frieze, and H. Kaplan, A new rounding procedure for the assignment problem with applications to dense graph arrangement problems, Proceedings of the 37-th Annual IEEE Symposium on Foundations of Computer Science (FOCS) , 1996, 21–30.
A. A. Assad, and W. Xu, On lower bounds for a class of quadratic 0–1 programs, Operations Research Letters 4 , 1985, 175–180.
E. Balas and J. B. Mazzola, Quadratic 0–1 programming by a new linearization, presented at the Joint ORSA/TIMS National Meeting , 1980, Washington D.C.
E. Balas and J. B. Mazzola, Nonlinear programming: I . Linearization techniques, Mathematical Programming 30 , 1984, 1–21.
E. Balas and J. B. Mazzola, Nonlinear programming: II. Dominance relations and algorithms, Mathematical Programming 30 , 1984, 2245.
A. I. Barvinok, Computational complexity of orbits in representations of symmetric groups, Advances in Soviet Mathematics 9 , 1992, 161–182.
MathSciNet Google Scholar
R. Battiti and G. Tecchiolli, The reactive tabu search, ORSA Journal on Computing 6 , 1994, 126–140.
M. S. Bazaraa and O. Kirca, Branch and bound based heuristics for solving the quadratic assignment problem, Naval Research Logistics Quarterly 30 , 1983, 287–304.
M. S. Bazaraa and H. D. Sherali, Benders’ partitioning scheme applied to a new formulation of the quadratic assignment problem, Naval Research Logistics Quarterly 27 , 1980, 29–41.
M. S. Bazaraa and H. D. Sherali, On the use of exact and heuristic cutting plane methods for the quadratic assignment problem, Journal of Operations Research Society 33 , 1982, 991–1003.
MATH MathSciNet Google Scholar
G. Birkhoff, Tres observaciones sobre el algebra lineal, Univ. Nac. Tucumán Rev., Ser. A , 1946, 147–151
B. Bollobâs, Extremal Graph Theory , Academic Press, London, 1978.
A. Bruengger, J. Clausen, A. Marzetta, and M. Perregaard, Joining forces in solving large-scale quadratic assignment problems in parallel, in Proceedings of the 11-th IEEE International Parallel Processing Symposium (IPPS) , 1997, 418–427.
E. S. Buffa, G. C. Armour, and T. E. Vollmann, Allocating facilities with CRAFT, Harvard Business Review 42, 1962, 136–158.
R. E. Burkard, Die Störungsmethode zur Lösung quadratischer Zuordnungsprobleme, Operations Research Verfahren 16 , 1973, 84–108.
R. E. Burkard, Quadratische Bottleneckprobleme, Operations Research Verfahren 18, 1974, 26–41.
R. E. Burkard, Locations with spatial interactions: the quadratic assignment problem, in Discrete Location Theory, P. B. Mirchandani and R. L. Francis, eds., Wiley, 1991.
R. E. Burkard and T. Bönniger, A heuristic for quadratic boolean programs with applications to quadratic assignment problems, European Journal of Operational Research 13, 1983, 374–386.
Article MATH Google Scholar
R. E. Burkard and E. Çela, Heuristics for biquadratic assignment problems and their computational comparison, European Journal of Operational Research 83 , 1995, 283–300.
R. E. Burkard, E. Çela, V. M. Demidenko, N. N. Metelski, and G. J. Woeginger, Perspectives of Easy and Hard Cases of the Quadratic Assignment Problems, SFB Report 104, Institute of Mathematics, Technical University Graz, Austria, 1997.
R. E. Burkard, E. Çela, and B. Klinz, On the biquadratic assignment problem, in Quadratic Assignment and Related Problems , P. M. Pardalos and H. Wolkowicz, eds., DIMACS Series on Discrete Mathematics and Theoretical Computer Science 16, 1994, 117–146, AMS, Providence, RI.
R. E. Burkard, E. Çela, G. Rote, and G. J. Woeginger, The quadratic assignment problem with an Anti-Monge and a Toeplitz matrix: Easy and hard cases, SFB Report 34, Institute of Mathematics, Technical University Graz, Austria, 1995. To appear in Mathematical Programming.
R. E. Burkard and U. Derigs, Assignment and matching problems: Solution methods with Fortran programs, Lecture Notes in Economics and Mathematical Systems 184, Springer-Verlag, Berlin, 1980.
R. E. Burkard and U. Fincke, On random quadratic bottleneck assignment problems, Mathematical Programming 23 , 1982, 227–232.
R. E. Burkard and U. Fincke, The asymptotic probabilistic behavior of the quadratic sum assignment problem, Zeitschrift für Operations Research 27, 1983, 73–81.
R. E. Burkard and U. Fincke, Probabilistic asymptotic properties of some combinatorial optimization problems, Discrete Applied Mathematics 12, 1985, 21–29.
R. E. Burkard, W. Hahn and U. Zimmermann, An algebraic approach to assignment problems, Mathematical Programming 12 , 1977, 318–327.
R. E. Burkard, S. E. Karisch, and F. Rendl, QAPLIB-a quadratic assignment prob- lem library, Journal of Global Optimization 10, 1997, 391–403. An on-line version is available via World Wide Web at the following URL: http://www.opt.math.tu-graz.ac.at/karisch/gaplib/
Article MathSciNet Google Scholar
R. E. Burkard, B. Klinz, and R. Rudolf, Perspectives of Monge properties in optimization, Discrete Applied Mathematics 70, 1996, 95–161.
R. E. Burkard and J. Offermann, Entwurf von Schreibmaschinentastaturen mittels quadratischer Zuordnungsprobleme, Zeitschrift für Operations Research 21 , 1977, B121–B132, (in German).
Article Google Scholar
R. E. Burkard and F. Rendl, A thermodynamically motivated simulation procedure for combinatorial optimization problems, European Journal Operational Research 17 , 1984, 169–174.
R. E. Burkard and U. Zimmermann, Combinatorial optimization in linearly ordered semimodules: a survey, in Modern Applied Mathematics , B. Korte, ed., North Holland, Amsterdam, 1982, 392–436.
P. Carraresi and F. Malucelli, A new lower bound for the quadratic assignment problem, Operations Research 40 , 1992, Suppl. No. 1 , S22–S27.
P. Carraresi and F. Malucelli, A reformulation scheme and new lower bounds for the QAP, in Quadratic Assignment and Related Problems , P. Pardalos and H. Wolkowicz, eds., DIMACS Series in Discrete Mathematics and Theoretical Computer Science 16 , 1994, 147–160, AMS, Providence, RI.
E. Çela, The Quadratic Assignment Problem: Theory and Algorithms , Kluwer Academic Publishers, Dordrecht, The Netherlands, 1998.
V. Cerny, Thermodynamical approach to the traveling salesman problem: An efficient simulation algorithm, Journal of Optimization Theory and Applications 45 , 1985, 41–51.
J. Chakrapani and J. Skorin-Kapov, Massively parallel tabu search for the quadratic assignment problem, Annals of Operations Research 41 , 1993, 327–342.
J. Chakrapani and J. Skorin-Kapov, A constructive method to improve lower bounds for the quadratic assignment problem, in Quadratic Assignment and Related Problems , P. Pardalos and H. Wolkowicz, eds., DIMACS Series in Discrete Mathematics and Theoretical Computer Science 16 , 1994, 161–171, AMS, Providence, RI.
P. Chretienne, A polynomial algorithm to optimally schedule tasks on a virtual distributed system under tree-like precedence constraints, European Journal of Operational Research 43 , 1989, 225–230.
N. Christofides, Worst case analysis of a new heuristic for the traveling salesman problem, Technical Report 338, Graduate School of Industrial Administration, Carnegie-Mellon University, Pittsburgh, PA, 1976.
N. Christofides and E. Benavent, An exact algorithm for the quadratic assignment problem, Operations Research 37 , 1989, 760–768.
N. Christofides and M. Gerrard, A graph theoretic analysis of bounds for the quadratic assignment problem, in Studies on Graphs and Discrete Programming , P. Hansen, ed., North Holland, 1981, pp. 61–68.
Chapter Google Scholar
J. Clausen, S. E. Karisch, M. Perregaard, and F. Rendl, On the applicability of lower bounds for solving rectilinear quadratic assignment problems in parallel, Computational Optimization and Applications 10 , 1998, 127–147.
J. Clausen and M. Perregaard, Solving large quadratic assignment problems in parallel, Computational Optimization and Applications 8 , 1997, 111–127.
A. Colorni, M. Dorigo, and V. Maniezzo, The ant system: optimization by a colony of cooperating agents, IEEE Transactions on Systems , Man , and Cybernetics -Part B 26 , 1996, 29–41.
A. Colorni and V. Maniezzo, The ant system applied to the quadratic assignment problem, to appear in IEEE Transactions on Knowledge and Data Engineering , 1998.
D. T. Connolly, An improved annealing scheme for the QAP, European Journal of Operational Research 46 , 1990, 93–100.
K. Conrad, Das Quadratische Zuweisungsproblem and zwei seiner Spezialfälle , Mohr-Siebeck, Tübingen, 1971.
D. Cyganski, R. F. Vaz, and V. G. Virball, Quadratic assignment problems with the Palubeckis’ algorithm are degenerate, IEEE Transactions on Circuits and Systems-I 41 , 1994, 481–484.
L. Davis, Genetic Algorithms and Simulated Annealing , Pitman, London, 1987.
V. G. Deineko and G. J. Woeginger, A solvable case of the quadratic assignment problem, SFB Report 88, Institute of Mathematics, Technical University Graz, Austria, 1996.
J. W. Dickey and J. W. Hopkins, Campus building arrangement using TOPAZ, Transportation Research 6 , 1972, 59–68.
M. Dorigo, Optimization, Learning, and Natural algorithms , Ph.D. Thesis, Dipartimento die Elettronica e Informazione, Politecnico di Milano, Milano, Italy, 1992, (in Italian).
M. E. Dyer, A. M. Frieze, and C. J. H. McDiarmid, On linear programs with random costs, Mathematical Programming 35 , 1986, 3–16.
C. S. Edwards, The derivation of a greedy approximator for the Koopmans-Beckmann quadratic assignment problem, Proceedings of the 77-th Combinatorial Programming Conference (CP77) , 1977, 55–86.
C. S. Edwards, A branch and bound algorithm for the Koopmans-Beckmann quadratic assignment problem, Mathematical Programming Study 13 , 1980, 35–52.
A. N. Elshafei, Hospital layout as a quadratic assignment problem, Operations Research Quarterly 28 , 1977, 167–179.
T. Espersen, S. E. Karisch, E. Cela, and J. Clausen, QAPPACK - a JAVA package for solving quadratic assignment problems, working paper, Department of Mathematical Modelling, Technical University of Denmark, Denmark, and Institute of Mathematics, Technical University Graz, Austria.
T. A. Feo, M. G. C. Resende, and S. H. Smith, A greedy randomized adaptive search procedure for the maximum independent set, Technical report, AT&T Bell Laboratories, Murray Hill, NJ, 1989. To appear in Operations Research .
T. A. Feo and M. G. C. Resende, Greedy randomized adaptive search procedures, Journal of Global Optimization 6 , 1995, 109–133.
G. Finke, R. E. Burkard, and F. Rendl, Quadratic assignment problems, Annals of Discrete Mathematics 31 , 1987, 61–82.
C. Fleurent and J. Ferland, Genetic hybrids for the quadratic assignment problem, in Quadratic Assignment and Related Problems , P. Pardalos and H. Wolkowicz, eds., DIMACS Series in Discrete Mathematics and Theoretical Computer Science 16 , 1994, 173–187, AMS, Providence, RI.
J. B. G. Frenk, M. van Houweninge, and A. H. G. Rinnooy Kan, Asymptotic properties of the quadratic assignment problem, Mathematics of Operations Research 10 , 1985, 100–116.
A. M. Frieze and J. Yadegar, On the quadratic assignment problem, Discrete Applied Mathematics 5 , 1983, 89–98.
A. M. Frieze, J. Yadegar, S. El-Horbaty, and D. Parkinson, Algorithms for assignment problems on an array processor, Parallel Computing 11 , 1989, 151–162.
L. M. Gambardella, E. D. Taillard, and M. Dorigo, Ant colonies for the QAP, Technical Report IDSIA-4–97, 1997, Istituto dalle Molle Di Studi sull’ Intelligenza Artificiale, Lugano, Switzerland.
M. R. Garey and D. S. Johnson, Computers and intractability: A guide to the theory of NP-completeness , W. H. Freeman and Company, New York, 1979.
J. W. Gavett and N. V. Plyter, The optimal assignment of facilities to locations by branch and bound, Operations Research 14 , 1966, 210–232.
A. M. Geoffrion, Lagrangean relaxation and its uses in integer programming, Mathematical Programming Study 2 , 1974, 82–114.
A. M. Geoffrion and G. W. Graves, Scheduling parallel production lines with changeover costs: Practical applications of a quadratic assignment/LP approach. Operations Research 24 , 1976, 595–610.
P. C. Gilmore, Optimal and suboptimal algorithms for the quadratic assignment problem, SIAM Journal on Applied Mathematics 10 , 1962, 305–313.
F. Glover, Improved linear integer programming formulations of nonlinear integer problems, Management Science 22 , 1975, 455–460.
F. Glover, Tabu search-Part I, ORSA Journal on Computing 1 , 1989, 190–206.
F. Glover, Tabu search-Part II, ORSA Journal on Computing 2 , 1989, 4–32.
F. Glover, M. Laguna, E. Taillard, and D. de Werra, eds., Tabu search, Annals of Operations Research 41 , 1993.
M. X. Goemans and D. P. Williamson, Improved approximation algorithms for maximum cut and satisfiability problems using semidefinite programming, Journal of the ACM 42 , 1995, 1115–1145.
D. E. Goldberg, Genetic Algorithms in Search , Optimization and Machine Learning , Addison-Wesley, Wokingham, England, 1989.
A. Graham, Kronecker Products and Matrix Calculus with Applications , Halsted Press, Toronto, 1981.
H. Greenberg, A quadratic assignment problem without column constraints, Naval Research Logistic Quarterly 16 , 1969, 417–422.
S. W. Hadley, Continuous Optimization Approaches for the Quadratic Assignment Problem , PhD thesis, University of Waterloo, Ontario, Canada, 1989.
S. W. Hadley, F. Rendl, and H. Wolkowicz, Bounds for the quadratic assignment problem using continuous optimization techniques, Proceedings of the 1-st Integer Programming and Combinatorial Optimization Conference (IPCO) , University of Waterloo Press, 1990, 237–248.
S. W. Hadley, F. Rendl, and H. Wolkowicz, A new lower bound via projection for the quadratic assignment problem, Mathematics of Operations Research 17 , 1992, 727–739.
S. W. Hadley, F. Rendl, and H. Wolkowicz, Nonsymmetric quadratic assignment problems and the Hoffman-Wielandt inequality, Linear Algebra and its Applications 58 , 1992, 109–124.
P. Hahn and T. Grant, Lower bounds for the quadratic assignment problem based upon a dual formulation, to appear in Operations Research.
P. Hahn, T. Grant, and N. Hall, Solution of the quadratic assignment problem using the Hungarian method, to appear in European Journal of Operational Research .
G. G. Hardy, J. E. Littlewood, and G. Pblya, Inequalities , Cambridge University Press, London and New York, 1952.
D. R. Hefiiey, Assigning runners to a relay team, in Optimal Strategies in Sports , S. P. Ladany and R. E. Machol, eds., North-Holland, Amsterdam, 1977, 169–171.
C. H. Heider, A computationally simplified pair exchange algorithm for the quadratic assignment problem, Paper No. 101, Center for Naval Analysis, Arlington, Virginia, 1972.
J. H. Holland, Adaptation in Natural and Artificial Systems , University of Michigan Press, Ann Arbor, 1975.
B. Jansen. A note on lower bounds for the QAP, Technical report, Mathematics and Computer Science, Delft University of Technology, The Netherlands, December 1993.
D. S. Johnson, C. H. Papadimitriou, and M. Yannakakis, How easy is local search, Journal of Computer and System Sciences 37 , 1988, 79–100.
T. A. Johnson, New linear programming-based solution procedures for the quadratic assignment problem, Ph.D. Thesis, Clemson University, SC, 1992.
M. Jünger, Polyhedral Combinatorics and the Acyclic Subdigraph Problem , Heldermann Verlag, Berlin, Germany, 1985.
M. Jünger and V. Kaibel, A basic study of the QAP polytope, Technical Report 96. 215, Institut für Informatik, Universität zu Köln, Germany, 1996.
M. Jünger and V. Kaibel, On the SQAP polytope, Technical Report 96. 241, Institut für Informatik, Universität zu Köln, Germany, 1996.
V. Kaibel, Polyhedral Combinatorics of the Quadratic Assignment Problem, Ph.D. Thesis, Universität zu Köln, Germany, 1997.
S. E. Karisch, Nonlinear Approaches for Quadratic Assignment and Graph Partition Problems, Ph.D. Thesis , Technical University Graz, Austria, 1995.
S. E. Karisch, E. Çela, J. Clausen, and T. Espersen, A dual framework for lower bounds of the quadratic assignment problem based on linearization, SFB Report 120, Institute of Mathematics, Technical University Graz, Austria, 1997.
S. E. Karisch and F. Rendl, Lower bounds for the quadratic assignment problem via triangle decompositions, Mathematical Programming 71 , 1995, 137–151.
S. E. Karisch, F. Rendl, and H. Wolkowicz, Trust regions and relaxations for the quadratic assignment problem, in Quadratic Assignment and Related Problems , P. Pardalos and H. Wolkowicz, eds., DIMACS Series in Discrete Mathematics and Theoretical Computer Science 16 , 1994, 199–220, AMS, Providence, RI.
R. M. Karp, Reducibility among combinatorial problems, in Complexity of Computer Computations , R. E. Miller and J. W. Thatcher, eds., Plenum, New York, 1972, 85–103.
L. Kaufmann and Fe Broeckx, An algorithm for the quadratic assignment problem using Benders’ decomposition, European Journal of Operational Research 2 , 1978, 204–211.
B. Kernighan and S. Lin, An efficient heuristic procedure for partitioning graphs, Bell Systems Journal 49 , 1972, 291–307.
S. Kirkpatrick, C. D. Gelatt, and M. P. Vecchi, Optimization by simulated annealing, Science 220 , 1983, 671–680.
J. G. Klincewicz, Avoiding local optima in the p-hub location problem using tabu search and GRASP , Annals of Operations 40 , 1992, 283–302.
J. G. Klincewicz and A. Rajan, Using GRASP to solve the component grouping problem, Technical report, AT&T Bell Laboratories, Holmdel, NJ, 1992.
T. C. Koopmans and M. J. Beckmann, Assignment problems and the location of economic activities, Econometrica 25 , 1957, 53–76.
J. Krarup and P. M. Pruzan, Computer-aided layout design, Mathematical Programming Study 9 , 1978, 75–94.
P. J. M. van Laarhoven and E. H. L. Aarts, Simulated Annealing: Theory and Applications , D. Reidel Publishing Company, Dordrecht, 1988.
A. M. Land, A problem of assignment with interrelated costs, Operations Research Quarterly 14 , 1963, 185–198.
G. Laporte and H. Mercure, Balancing hydraulic turbine runners: A quadratic assignment problem, European Journal of Operational Research 35 , 1988, 378–382.
E. L. Lawler, The quadratic assignment problem, Management Science 9 , 1963, 586–599.
E. L. Lawler, J. K. Lenstra, A. H. G. Rinnooy Kan, and D. B. Shmoys, eds., The Traveling Salesman Problem , Wiley, Chichester, 1985.
T. Lengauer, Combinatorial Algorithms for Intergrated Circuit Layout , Wiley, Chichester, 1990.
W. Leontief, Input-Output Economics , Oxford University Press, New York, 1966.
Y. Li and P. M. Pardalos, Generating quadratic assignment test problems with known optimal permutations, Computational Optimization and Applications 1 , 1992, 163–184.
Y. Li, P. M. Pardalos, K. G. Ramakrishnan, and M. G. C. Resende, Lower bounds for the quadratic assignment problem, Annals of Operations Research 50 , 1994, 387–410.
Y. Li, P. M. Pardalos, and M. G. C. Resende, A greedy randomized adaptive search procedure for the quadratic assignment problem, in Quadratic Assignment and Related Problems , P. Pardalos and H. Wolkowicz, eds., DIMACS Series in Discrete Mathematics and Theoretical Computer Science 16 1994, 237–261, AMS, Providence, RI.
L. Lovâsz and A. Schrijver, Cones of matrices and set functions and 0–1 optimization, SIAM Journal on Optimization 1 , 1991, 166–190.
E. J. McCormick, Human Factors Engineering , McGraw-Hill, New York, 1970.
T. Magnanti, R. Ahuja, and J. Orlin. Network flows: theory, algorithms, and applications , Prentice Hall, Englewood-Cliffs, New Jersey, 1993.
F. Malucelli, Quadratic Assignment Problems: Solution Methods and Applications, Ph.D. Thesis, Dipartimento di Informatica, Universitâ di Pisa, Italy, 1993.
F. Malucelli and D. Pretolani, Lower bounds for the quadratic semi-assignment problem, Technical Report 955, Centre des Recherches sur les Transports, Université de Montréal, Canada, 1993.
A. Marzetta, Dynamic programming for the quadratic assignment problem, presented at the 2-nd Aussois Workshop on Combinatorial Optimization, 1998, Aussois, France.
T. Mautor and C. Roucairol, A new exact algorithm for the solution of quadratic assignment problems, Discrete Applied Mathematics 55 , 1992, 281–293.
T. Mavridou, P. M. Pardalos, L. S. Pitsoulis, and M. G. C. Resende, A GRASP for the biquadratic assignment problem, European Journal of Operations Research 105 , 1998, 613–621.
N. Metropolis, A. Rosenbluth, M. Rosenbluth, A. Teller, and E. Teller, Equations of state calculations by fast computing machines, Journal of Chemical Physics 21 , 1953, 1087–1092.
I. Z. Milis and V. F. Magirou, A Lagrangean relaxation algorithm for sparse quadratic assignment problems, Operations Research Letters 17 , 1995, 69–76.
P. B. Mirchandani and T. Obata, Locational decisions with interactions between facilities: the quadratic assignment problem a review, Working Paper Ps-79–1, Rensselaer Polytechnic Institute, Troy, New York, May 1979.
L. Mirsky, The spread of a matrix, Mathematika 3 , 1956, 127–130.
J. Mosevich, Balancing hydraulic turbine runners — a discrete combinatorial optimization problem, European Journal of Operational Research 26 , 1986, 202–204.
K. A. Murthy, P. Pardalos, and Y. Li, A local search algorithm for the quadratic assignment problem, Informatica 3 , 1992, 524–538.
K. G. Murty, An algorithm for ranking all the assignments in order of increasing cost, Operations Research 16 , 1968, 682–287.
H. Müller-Merbach, Optimale Reihenfolgen , Springer-Verlag, Berlin, Heidelberg, New York, 1970, pp. 158–171.
C. E. Nugent, T. E. Vollmann, and J. Ruml, An experimental comparison of techniques for the assignment of facilities to locations, Journal of Operations Research 16 , 1969, 150–173.
M. W. Padberg and M. P. Rijal, Location , Scheduling , Design and Integer Programming , Kluwer Academic Publishers, Boston, 1996.
Book MATH Google Scholar
M. W. Padberg and G. Rinaldi, Optimization of a 532-city symmetric traveling salesman problem by a branch and cut algorithm, Operations Research Letters 6 , 1987, 1–7.
G. S. Palubeckis, Generation of quadratic assignment test problems with known optimal solutions, U.S.S.R. Comput. Maths. Math. Phys . 28 , 1988, 97–98, (in Russian).
C. H. Papadimitriou and D. Wolfe, The complexity of facets resolved, Proceedings of the 25-th Annual IEEE Symposium on the Foundations of Computer Science (FOCS) , 1985, 74–78.
P. Pardalos and J. Crouse, A parallel algorithm for the quadratic assignment problem, Proceedings of the Supercomputing Conference 1989 , ACM Press, 1989, 351–360.
P. Pardalos, F. Rendl, and H. Wolkowicz, The quadratic assignment problem: A survey and recent developments, in Quadratic Assignment and Related Problems, P. Pardalos and H. Wolkowicz, eds., DIMACS Series in Discrete Mathematics and Theoretical Computer Science 16 , 1994, 1–42, AMS, Providence, RI.
P. M. Pardalos, L. S. Pitsoulis, and M. G. C. Resende, A parallel GRASP implementation for solving the quadratic assignment problem, in Parallel Algorithms for Irregular Problems: State of the Art, A. Ferreira and José D.P. Rolim, eds., Kluwer Academic Publishers, 1995, 115–133.
P. M. Pardalos, L. S. Pitsoulis, and M. G. C. Resende, Fortran subroutines for approximate solution of sparse quadratic assignment problems using GRASP, ACM Transcations on Mathematical Software 23 , 1997, 196–208.
P. M. Pardalos, K. G. Ramakrishnan, M. G. C. Resende, and Y. Li, Implementation of a variable reduction based lower bound in a branch and bound algorithm for the quadratic assignment problem, SIAM Journal on Optimization 7, 1997, 280–294.
P. M. Pardalos and J. Xue, The maximum clique problem, Research Report 93–1, Department of Industrial and System Engineering, University of Florida, Fl, 1993.
M. Queyranne, Performance ratio of heuristics for triangle inequality quadratic assignment problems, Operations Research Letters 4, 1986, 231–234.
G. Reinelt, The Linear Ordering Problem: Algorithms and Applications , Heldermann Verlag, Berlin, Germany, 1985.
F. Rendl, Ranking scalar products to improve bounds for the quadratic assignment problem, European Journal of Operations Research 20 , 1985, 363–372.
F. Rendl and H. Wolkowicz, Applications of parametric programming and eigenvalue maximization to the quadratic assignment problem, Mathematical Programming 53 , 1992, 63–78.
M. G. C. Resende, P. M. Pardalos, and Y. Li, Fortran subroutines for approximate solution of dense quadratic assignment problems using GRASP, ACM Transcations on Mathematical Software 22 , 1996, 104–118.
M. G. C. Resende, L. S. Pitsoulis, and P. M. Pardalos, Approximate solution of weighted max-sat problems using GRASP, in The Satisfiability Problem , P. M. Pardalos, M. G. C. Resende and D. Z. Du, eds., DIMACS Series in Discrete Mathematics and Theoretical Computer Science 35 , 1997, 393–405, AMS, Providence, RI.
M. G. C. Resende, K. G. Ramakrishnan, and Z. Drezner, Computing lower bounds for the quadratic assignment problem with an inte-rior point algorithm for linear programming, Operations Research 43 , 1995, 781–791.
W. T. Rhee, A note on asymptotic properties of the quadratic assignment problem, Operations Research Letters 7 , 1988, 197–200.
W. T. Rhee, Stochastic analysis of the quadratic assignment problem, Mathematics of Operations Research 16 , 1991, 223–239.
M. P. Rijal, Scheduling, Design and Assignment Problems with Quadratic Costs, Ph.D . Thesis, New York University, NY, 1995.
C. Roucairol, A reduction method for quadratic assignment problems, Operations Research Verfahren 32 , 1979, 183–187.
C. Roucairol, A parallel branch and bound algorithm for the quadratic assignment problem, Discrete Applied Mathematics 18 , 1987, 221–225.
S. Sahni and T. Gonzalez, P-complete approximation problems, Journal of the Association of Computing Machinery 23 , 1976, 555–565.
A. Schäffer and M. Yannakakis, Simple local search problems that are hard to solve, SIAM Journal on Computing 20 , 1991, 56–87.
J. Skorin-Kapov, Tabu search applied to the quadratic assignment problem, ORSA Journal on Computing 2 , 1990, 33–45.
J. Skorin-Kapov, Extensions of tabu search adaptation to the quadratic assignment problem, to appear in Computers and Operations Research .
L. Steinberg, The backboard wiring problem: A placement algorithm, SIAM Review 3 , 1961, 37–50.
H. S. Stone, Multiprocessor scheduling with the aid of network flow algorithms, IEEE Transactions on Software Engineering 3 , 1977, 8593.
W. Szpankowski, Combinatorial optimization problems for which almost every algorithm is asymptotically optimall, Optimization 33 , 1995, 359–367.
E. Taillard, Robust tabu search for the quadratic assignment problem, Parallel Computing 17 , 1991, 443–455.
D. M. Tate and A. E. Smith, A genetic approach to the quadratic assignment problem, Computers and Operations Research 22 , 1995, 73–83.
I. Ugi, J. Bauer, J. Friedrich, J. Gasteiger, C. Jochum, and W. Schubert, Neue Anwendungsgebiete für Computer in der Chemie, Angewandte Chemie 91 , 1979, 99–111.
D. H. West, Algorithm 608: Approximate solution of the quadratic assignment problem, ACM Transactions on Mathematical Software 9 , 1983, 461–466.
M. R. Wilhelm and T. L. Ward, Solving quadratic assignment problems by simulated annealing, IEEE Transactions 19 , 1987, 107–119.
Q. Zhao, Semidefinite Programming for Assignment and Partitioning Problems, Ph.D . Thesis, University of Waterloo, Ontario, Canada, 1996.
Q. Zhao, S. E. Karisch, F. Rendl, and H. Wolkowicz, Semidefinite relaxations for the quadratic assignment problem, Technical Report DIKU TR-96–32, Department of Computer Science, University of Copenhagen, Denmark, 1996. To appear in Journal of Combinatorial Optimization .
Download references
Author information
Authors and affiliations.
Institute of Mathematics, Technical University Graz, Steyrergasse 30, 8010, Graz, Austria
Rainer E. Burkard & Eranda Çela
Center for Applied Optimization, Industrial and Systems Engineering Department, University of Florida, Gainesville, FL, 32611, USA
Panos M. Pardalos & Leonidas S. Pitsoulis
You can also search for this author in PubMed Google Scholar
Editor information
Editors and affiliations.
University of Minnesota, Minneapolis, USA
Ding-Zhu Du
University of Florida, Gainesville, USA
Panos M. Pardalos
Rights and permissions
Reprints and permissions
Copyright information
© 1998 Kluwer Academic Publishers
About this chapter
Burkard, R.E., Çela, E., Pardalos, P.M., Pitsoulis, L.S. (1998). The Quadratic Assignment Problem. In: Du, DZ., Pardalos, P.M. (eds) Handbook of Combinatorial Optimization. Springer, Boston, MA. https://doi.org/10.1007/978-1-4613-0303-9_27
Download citation
DOI : https://doi.org/10.1007/978-1-4613-0303-9_27
Publisher Name : Springer, Boston, MA
Print ISBN : 978-1-4613-7987-4
Online ISBN : 978-1-4613-0303-9
eBook Packages : Springer Book Archive
Share this chapter
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Publish with us
Policies and ethics
- Find a journal
- Track your research
quadratic_assignment(method=’faq’) #
Solve the quadratic assignment problem (approximately).
This function solves the Quadratic Assignment Problem (QAP) and the Graph Matching Problem (GMP) using the Fast Approximate QAP Algorithm (FAQ) [1] .
Quadratic assignment solves problems of the following form:
where \(\mathcal{P}\) is the set of all permutation matrices, and \(A\) and \(B\) are square matrices.
Graph matching tries to maximize the same objective function. This algorithm can be thought of as finding the alignment of the nodes of two graphs that minimizes the number of induced edge disagreements, or, in the case of weighted graphs, the sum of squared edge weight differences.
Note that the quadratic assignment problem is NP-hard. The results given here are approximations and are not guaranteed to be optimal.
The square matrix \(A\) in the objective function above.
The square matrix \(B\) in the objective function above.
The algorithm used to solve the problem. This is the method-specific documentation for ‘faq’. ‘2opt’ is also available.
OptimizeResult containing the following fields.
Column indices corresponding to the best permutation found of the nodes of B .
The objective value of the solution.
The number of Frank-Wolfe iterations performed.
For documentation for the rest of the parameters, see scipy.optimize.quadratic_assignment
Maximizes the objective function if True .
Fixes part of the matching. Also known as a “seed” [2] .
Each row of partial_match specifies a pair of matched nodes: node partial_match[i, 0] of A is matched to node partial_match[i, 1] of B . The array has shape (m, 2) , where m is not greater than the number of nodes, \(n\) .
numpy.random.RandomState }, optional
If seed is None (or np.random ), the numpy.random.RandomState singleton is used. If seed is an int, a new RandomState instance is used, seeded with seed . If seed is already a Generator or RandomState instance then that instance is used.
Initial position. Must be a doubly-stochastic matrix [3] .
If the initial position is an array, it must be a doubly stochastic matrix of size \(m' \times m'\) where \(m' = n - m\) .
If "barycenter" (default), the initial position is the barycenter of the Birkhoff polytope (the space of doubly stochastic matrices). This is a \(m' \times m'\) matrix with all entries equal to \(1 / m'\) .
If "randomized" the initial search position is \(P_0 = (J + K) / 2\) , where \(J\) is the barycenter and \(K\) is a random doubly stochastic matrix.
Set to True to resolve degenerate gradients randomly. For non-degenerate gradients this option has no effect.
Integer specifying the max number of Frank-Wolfe iterations performed.
Tolerance for termination. Frank-Wolfe iteration terminates when \(\frac{||P_{i}-P_{i+1}||_F}{\sqrt{m')}} \leq tol\) , where \(i\) is the iteration number.
The algorithm may be sensitive to the initial permutation matrix (or search “position”) due to the possibility of several local minima within the feasible region. A barycenter initialization is more likely to result in a better solution than a single random initialization. However, calling quadratic_assignment several times with different random initializations may result in a better optimum at the cost of longer total execution time.
J.T. Vogelstein, J.M. Conroy, V. Lyzinski, L.J. Podrazik, S.G. Kratzer, E.T. Harley, D.E. Fishkind, R.J. Vogelstein, and C.E. Priebe, “Fast approximate quadratic programming for graph matching,” PLOS one, vol. 10, no. 4, p. e0121002, 2015, DOI:10.1371/journal.pone.0121002
D. Fishkind, S. Adali, H. Patsolic, L. Meng, D. Singh, V. Lyzinski, C. Priebe, “Seeded graph matching”, Pattern Recognit. 87 (2019): 203-215, DOI:10.1016/j.patcog.2018.09.014
“Doubly stochastic Matrix,” Wikipedia. https://en.wikipedia.org/wiki/Doubly_stochastic_matrix
As mentioned above, a barycenter initialization often results in a better solution than a single random initialization.
However, consider running from several randomized initializations and keeping the best result.
The ‘2-opt’ method can be used to further refine the results.
Help | Advanced Search
Computer Science > Machine Learning
Title: learning solution-aware transformers for efficiently solving quadratic assignment problem.
Abstract: Recently various optimization problems, such as Mixed Integer Linear Programming Problems (MILPs), have undergone comprehensive investigation, leveraging the capabilities of machine learning. This work focuses on learning-based solutions for efficiently solving the Quadratic Assignment Problem (QAPs), which stands as a formidable challenge in combinatorial optimization. While many instances of simpler problems admit fully polynomial-time approximate solution (FPTAS), QAP is shown to be strongly NP-hard. Even finding a FPTAS for QAP is difficult, in the sense that the existence of a FPTAS implies $P = NP$. Current research on QAPs suffer from limited scale and computational inefficiency. To attack the aforementioned issues, we here propose the first solution of its kind for QAP in the learn-to-improve category. This work encodes facility and location nodes separately, instead of forming computationally intensive association graphs prevalent in current approaches. This design choice enables scalability to larger problem sizes. Furthermore, a \textbf{S}olution \textbf{AW}are \textbf{T}ransformer (SAWT) architecture integrates the incumbent solution matrix with the attention score to effectively capture higher-order information of the QAPs. Our model's effectiveness is validated through extensive experiments on self-generated QAP instances of varying sizes and the QAPLIB benchmark.
| Comments: | Accepted by ICML 2024 |
| Subjects: | Machine Learning (cs.LG); Artificial Intelligence (cs.AI) |
| Cite as: | [cs.LG] |
| (or [cs.LG] for this version) | |
| Focus to learn more arXiv-issued DOI via DataCite |
Submission history
Access paper:.
- HTML (experimental)
- Other Formats
References & Citations
- Google Scholar
- Semantic Scholar
BibTeX formatted citation
Bibliographic and Citation Tools
Code, data and media associated with this article, recommenders and search tools.
- Institution
arXivLabs: experimental projects with community collaborators
arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.
Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.
Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .

IMAGES
VIDEO
COMMENTS
The quadratic assignment problem (QAP) is one of the fundamental combinatorial optimization problems in the branch of optimization or operations research in mathematics, from the category of the facilities location problems first introduced by Koopmans and Beckmann.. The problem models the following real-life problem: There are a set of n facilities and a set of n locations.
The assignment problem is a fundamental combinatorial optimization problem. In its most general form, the problem is as follows: The problem instance has a number of agents and a number of tasks. Any agent can be assigned to perform any task, incurring some cost that may vary depending on the agent-task assignment.
The Quadratic Assignment Problem (QAP), discovered by Koopmans and Beckmann in 1957, is a mathematical optimization module created to describe the location of invisible economic activities. An NP-Complete problem, this model can be applied to many other optimization problems outside of the field of economics. It has been used to optimize ...
The Quadratic Assignment Problem (QAP) is an optimization problem that deals with assigning a set of facilities to a set of locations, considering the pairwise distances and flows between them. The problem is to find the assignment that minimizes the total cost or distance, taking into account both the distances and the flows. The distance ...
The quadratic assignment problem (QAP) was introduced by Koopmans and Beckmann in 1957 as a mathematical model for the location of a set of indivisible economical activities [113]. Consider the problem of allocating a set of facilities to a set of locations, with the
The quadratic assignment problem (QAP) was introduced by Koopmans and Beckmann in 1957 as a mathematical model for the location of indivisible economical activities [].Consider the problem of allocating n facilities to n locations, with the cost being a function of the distance and flow between the facilities plus costs associated with placing a facility at a certain location.
The quadratic assignment problem (QAP) is a combinatorial optimization problem, that although there is a substantial amount of research devoted to it, it is still, up to this date, not well solvable in the sense that no exact algorithm can solve problems of size n > 20 in reasonable computational time. The QAP can be viewed as a natural extension of the linear assignment problem (LAP; cf. also ...
The quadratic assignment problem introduced by Koopmans and Beckmann (1957) has the following form: (1) (2) and fik is the flow between facilities i and k, djl is the distance between locations j and l, and cij is the cost of placing facility i at location j. The variable xij = 1 if facility i is assigned to location j, otherwise, xij = 0 and N ...
The Hungarian method is a combinatorial optimization algorithm that solves the assignment problem in polynomial time and which anticipated later primal-dual methods.It was developed and published in 1955 by Harold Kuhn, who gave it the name "Hungarian method" because the algorithm was largely based on the earlier works of two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry.
travelling salesman problem, graph isomorphism and graph packing problem [1]. The QAP problem has been shown to be NP-hard [2], hence several approaches have been used to solve this problem. Intensive studies on quadratic assignment problems produced many algorithms over the last few decades. For a survey on these methods, see [3,4].
A wide variety of practical problems in design, planning, and management can be formulated as quadratic assignment problems, and this paper discusses this class of problem. Since algorithms for producing optimal solutions to such problems are computationally infeasible for all but small problems of this type, heuristic techniques must usually ...
The quadratic assignment problem (QAP) was introduced in 1957 by Koopmans and Beckmann to model a plant location problem. Since then the QAP has been object of numerous investigations by mathematicians, computers scientists, ope- tions researchers and practitioners. Nowadays the QAP is widely considered as a classical combinatorial optimization ...
The Quadratic Assignment Problem (QAP), introduced by Koopmans and Beckmann (1957), consists in minimizing a cost function expressed by the distance and the flow between each pair of facilities assigned to their respective sites. The QAP is a well-known and well-studied problem, being considered as one of the most difficult to solve in ...
The quadratic assignment problem (QAP) is considered one of the most difficult optimization problems to solve optimally. The QAP is a combinatorial optimization problem stated for the first time by Koopmans and Beckmann ().Early papers on the subject include Gilmore (), Pierce and Crowston (), Lawler (), and Love and Wong ().The problem is defined as follows.
The Quadratic Assignment Problem: A Survey and Recent Developments, in Quadratic Assignment and Related Problems, DIMACS Series in Discrete Mathematics and Theoretical Computer Science, Volume 16, 1994. P. Hahn, T. Grant, and N. Hall. A Branch-and-Bound Algorithm for the Quadratic Assignment Problem Based on the Hungarian Method, European ...
Note that the quadratic assignment problem is NP-hard. The results given here are approximations and are not guaranteed to be optimal. Parameters: A 2-D array, square. The square matrix \(A\) in the objective function above. B 2-D array, square. The square matrix \(B\) in the objective function above. method str in {'faq', '2opt ...
In mathematics, the quadratic bottleneck assignment problem ( QBAP) is one of the fundamental combinatorial optimization problems in the branch of optimization or operations research, from the category of the facilities location problems. [1] It is related to the quadratic assignment problem in the same way as the linear bottleneck assignment ...
The quadratic assignment problem (QAP) is a combinatorial optimization problem, that although there is a substantial amount of research devoted to it, it is still, up to this date, not well solvable in the sense that no exact algorithm can solve problems of size n > 20 in reasonable computational time. The QAP can be ...
For Quadratic Assignment, one has a (Linear) Assignment, solvable in O(n 3/2) time by classical methods (recall that n is the number of entries in the Assignment cost matrix); see e.g. [20]. The corresponding bound is known as the Gilmore-Lawler bound [15] , [22] (typically presented as a lower bound since Quadratic Assignment is mainly ...
Abstract. The quadratic assignment problem (QAP) was introduced by Koopmans and Beckmann in 1957 as a mathematical model for the location of a set of indivisible economical activities [113]. Consider the problem of allocating a set of facilities to a set of locations, with the cost being a function of the distance and flow between the ...
Note that the quadratic assignment problem is NP-hard. The results given here are approximations and are not guaranteed to be optimal. Parameters: A 2-D array, square. The square matrix \(A\) in the objective function above. B 2-D array, square. The square matrix \(B\) in the objective function above. method str in {'faq', '2opt ...
Note that the quadratic assignment problem is NP-hard. The results given here are approximations and are not guaranteed to be optimal. Parameters: A 2-D array, square. The square matrix \(A\) in the objective function above. B 2-D array, square. The square matrix \(B\) in the objective function above. method str in {'faq', '2opt ...
Quadratic unconstrained binary optimization (QUBO), also known as unconstrained binary quadratic programming (UBQP), is a combinatorial optimization problem with a wide range of applications from finance and economics to machine learning. QUBO is an NP hard problem, and for many classical problems from theoretical computer science, like maximum cut, graph coloring and the partition problem ...
Recently various optimization problems, such as Mixed Integer Linear Programming Problems (MILPs), have undergone comprehensive investigation, leveraging the capabilities of machine learning. This work focuses on learning-based solutions for efficiently solving the Quadratic Assignment Problem (QAPs), which stands as a formidable challenge in combinatorial optimization. While many instances of ...