An IERI – International Educational Research Institute Journal
- Open access
- Published: 10 December 2014

The acquisition of problem solving competence: evidence from 41 countries that math and science education matters
- Ronny Scherer 1 , 2 &
- Jens F Beckmann 3
Large-scale Assessments in Education volume 2 , Article number: 10 ( 2014 ) Cite this article
14k Accesses
16 Citations
1 Altmetric
Metrics details
On the basis of a ‘problem solving as an educational outcome’ point of view, we analyse the contribution of math and science competence to analytical problem-solving competence and link the acquisition of problem solving competence to the coherence between math and science education. We propose the concept of math-science coherence and explore whether society-, curriculum-, and school-related factors confound with its relation to problem solving.
By using the PISA 2003 data set of 41 countries, we apply multilevel regression and confounder analyses to investigate these effects for each country.
Our results show that (1) math and science competence significantly contribute to problem solving across countries; (2) math-science coherence is significantly related to problem solving competence; (3) country-specific characteristics confound this relation; (4) math-science coherence is linked to capability under-utilisation based on science performance but less on math performance.
Conclusions
In sum, low problem solving scores seem a result of an impeded transfer of subjectspecific knowledge and skills (i.e., under-utilisation of science capabilities in the acquisition of problem solving competence), which is characterised by low levels of math-science coherence.
The ability to solve real-world problems and to transfer problem-solving strategies from domain-specific to domain-general contexts and vice versa has been regarded an important competence students should develop during their education in school (Greiff et al. [ 2013 ]; van Merriënboer [ 2013 ]). In the context of large-scale assessments such as the PISA study problem solving competence is defined as the ability to solve cross-disciplinary and real-world problems by applying cognitive skills such as reasoning and logical thinking (Jonassen [ 2011 ]; OECD [ 2004 ]). Since this competence is regarded a desirable educational outcome, especially math and science educators have focused on developing students’ problem solving and reasoning competence in their respective domain-specific contexts (e.g., Kind [ 2013 ]; Kuo et al. [ 2013 ]; Wu and Adams [ 2006 ]). Accordingly, different conceptual frameworks were proposed that describe the cognitive processes of problem solving such as understanding the problem, building adequate representations of the problem, developing hypotheses, conducting experiments, and evaluating the solution (Jonassen [ 2011 ]; OECD [ 2005 ]). In comparing these approaches in math and science, it seems apparent that there is a conceptual overlap between the problem solving models in these two domains. This overlap triggers the question regarding its contribution to the development of students’ cross-curricular problem-solving competence (Abd-El-Khalick et al. [ 2004 ]; Bassok and Holyoak [ 1993 ]; Hiebert et al. [ 1996 ]).
The operationalization and scaling of performance in PISA assessments enables direct contrasting of scores in students’ competences in math and problem solving. Leutner et al. ([ 2012 ]) suggest that discrepancies between math and problem solving scores are indicative of the relative effectiveness of math education (OECD [ 2004 ]). In line with a “Capability-Utilisation Hypothesis”, it is assumed that math scores that negatively deviate from their problem solving counterpart signify an under-utilisation of students’ problem-solving capabilities as indicated by their scores in generic problem solving.
We intend to extend this view in two ways: First, by introducing the concept of math-science coherence we draw the focus on the potential synergistic link between math and science education and its contribution to the acquisition of problem solving competence. Second, the introduction of a Capability Under-Utilisation Index will enable us to extend the focus of the Capability-Utilisation Hypothesis to both, math and science education. The combination of the concept of math-science coherence with the notion of capability-utilisation will help to further explore the facilitating processes involved in the transition of subject-specific knowledge and skills to the acquisition of problem solving competence. These insights are expected to contribute to a better understanding of meaningful strategies to improve and optimize educational systems in different countries.
Theoretical framework
Problem solving as an educational goal.
In the PISA 2003 framework, problem solving is referred to as “an individual’s capacity to use cognitive processes to resolve real, cross-disciplinary situations where the solution path is not immediately obvious” (OECD [ 2004 ], p. 156). This definition is based on the assumption of domain-general skills and strategies that can be employed in various situations and contexts. These skills and strategies involve cognitive processes such as: Understanding and characterizing the problem, representing the problem, solving the problem, reflecting and communicating the problem solution (OECD [ 2003 ]). Problem solving is often regarded a process rather than an educational outcome, particularly in research on the assessment and instruction of problem solving (e.g., Greiff et al. [ 2013 ]; Jonassen [ 2011 ]). This understanding of the construct is based on the assumption that problem solvers need to perform an adaptive sequence of cognitive steps in order to solve a specific problem (Jonassen [ 2011 ]). Although problem solving has also been regarded as a process skill in large-scale assessments such as the PISA 2003 study, these assessments mainly focus on problem solving performance as an outcome that can be used for international comparisons (OECD [ 2004 ]). However, problem solving competence was operationalized as a construct comprised of cognitive processes. In the context of the PISA 2003 study, these processes were referred to as analytical problem solving, which was assessed by static tasks presented in paper-and-pencil format. Analytical problem-solving competence is related to school achievement and the development of higher-order thinking skills (e.g., Baumert et al. [ 2009 ]; OECD [ 2004 ]; Zohar [ 2013 ]). Accordingly, teachers and educators have focused on models of problem solving as guidelines for structuring inquiry-based processes in their subject lessons (Oser and Baeriswyl [ 2001 ]). Van Merriënboer ([ 2013 ]) pointed out that problem solving should not only be regarded a mere instructional method but also as a major educational goal. Recent curricular reforms have therefore shifted towards the development of problem solving abilities in school (Gallagher et al. [ 2012 ]; Koeppen et al. [ 2008 ]). These reforms were coupled with attempts to strengthen the development of transferable skills that can be applied in real-life contexts (Pellegrino and Hilton [ 2012 ]). For instance, in the context of 21 st century skills, researchers and policy makers have agreed on putting emphasis on fostering skills such as critical thinking, digital competence, and problem solving (e.g., Griffin et al. [ 2012 ]). In light of the growing importance of lifelong learning and the increased complexity of work- and real-life problem situations, these skills are now regarded as essential (Griffin et al. [ 2012 ]; OECD [ 2004 ]). Hence, large-scale educational studies such as PISA have shifted towards the assessment and evaluation of problem solving competence as a 21 st century skill.
The PISA frameworks of math and science competence
In large-scale assessments such as the PISA studies, students’ achievement in the domains of science and mathematics play an important role. Moreover, scientific and mathematical literacy are now regarded essential to being a reflective citizen (Bybee [ 2004 ]; OECD [ 2003 ]). Generally, Baumert et al. ([ 2009 ]) have shown that students’ math and science achievements are highly related to domain-general ability constructs such as reasoning or intelligence. In this context, student achievement refers to “the result of domain-specific processes of knowledge acquisition and information processing” (cf. Baumert et al. [ 2009 ], p. 169). This line of argument is reflected in definitions and frameworks of scientific and mathematical literacy, which are conceptualized as domain-specific competences that are hierarchically organized and build upon abilities closely related to problem solving (Brunner et al. [ 2013 ]).
Scientific literacy has been defined within a multidimensional framework, differentiating between three main cognitive processes, namely describing, explaining, and predicting scientific phenomena, understanding scientific investigations, and interpreting scientific evidence and conclusions (OECD [ 2003 ]). In addition, various types of knowledge such as ‘knowledge about the nature of science’ are considered as factors influencing students’ achievements in this domain (Kind [ 2013 ]). We conclude that the concept of scientific literacy encompasses domain-general problem-solving processes, elements of scientific inquiry (Abd-El-Khalick et al. [ 2004 ]; Nentwig et al. [ 2009 ]), and domain-specific knowledge.
The definition of mathematical literacy refers to students’ competence to utilise mathematical modelling and mathematics in problem-solving situations (OECD [ 2003 ]). Here, we can also identify overlaps between cognitive processes involved in mathematical problem solving and problem solving in general: Structuring, mathematizing, processing, interpreting, and validating (Baumert et al. [ 2009 ]; Hiebert et al. [ 1996 ]; Kuo et al. [ 2013 ]; Polya [ 1945 ]). In short, mathematical literacy goes beyond computational skills (Hickendorff [ 2013 ]; Wu and Adams [ 2006 ]) and is conceptually linked to problem solving.
In the PISA 2003 framework, the three constructs of math, science, and problem solving competence overlap conceptually. For instance, solving the math items requires reasoning, which comprises analytical skills and information processing. Given the different dimensions of the scientific literacy framework, the abilities involved in solving the science items are also related to problem solving, since they refer to the application of knowledge and the performance of inquiry processes (OECD [ 2003 ]). This conceptual overlap is empirically supported by high correlations between math and problem solving ( r = .89) and between science and problem solving ( r = .80) obtained for the sample of 41 countries involved in PISA 2003 (OECD [ 2004 ]). The relation between math and science competence was also high ( r = .83). On the one hand, the sizes of the inter-relationships, give rise to the question regarding the uniqueness of each of the competence measures. On the other hand, the high correlations indicate that problem-solving skills are relevant in math and science (Martin et al. [ 2012 ]). Although Baumert et al. ([ 2009 ]) suggest that the domain-specific competences in math and science require skills beyond problem solving (e.g., the application of domain-specific knowledge) we argue from an assessment perspective that the PISA 2003 tests in math, science, and problem solving measure predominantly basic academic skills relatively independent from academic knowledge (see also Bulle [ 2011 ]).
The concept of capability-utilisation
Discrepancies between students’ performance in math/science and problem solving were studied at country level (OECD [ 2004 ]) and were, for example for math and problem solving scores, interpreted in two ways: (1) If students’ perform better in math than in problem solving, they would “have a better grasp of mathematics content […] after accounting for the level of generic problem-solving skills…” (OECD [ 2004 ], p. 55); (2) If students’ estimated problem-solving competence is higher than their estimated math competence, “… this may suggest that students have the potential to achieve better results in mathematics than that reflected in their current performance…” (OECD [ 2004 ], p. 55). Whilst the latter discrepancy constitutes a capability under-utilisation in math, the former suggests challenges in utilising knowledge and skills acquired in domain-specific contexts in domain-unspecific contexts (i.e., transfer problem).
To quantify the degree to which students are able to transfer their problem solving capabilities from domain-specific problems in math or science to cross-curricular problems, we introduce the Capability Under-Utilisation Index (CUUI) as the relative difference between math or science and problem solving scores:
A positive CUUI indicates that the subject-specific education (i.e., math or science) in a country tends to under-utilise its students’ capabilities to problem solve. A negative CUUI indicates that a country’s educational system fails to fully utilise its students’ capabilities to acquire math and science literacy in the development of problem solving. The CUUI reflects the relative discrepancies between the achievement scores in different domains a .
The concept of math-science coherence
In light of the conceptual and empirical discussion on the relationship between math, science, and problem solving competence, we introduce the concept of math-science coherence as follows: First, math-science coherence refers to the set of cognitive processes involved in both subjects and thus represents processes which are related to reasoning and information processing, relatively independent from domain-specific knowledge. Second, math-science coherence reflects the degree to which math and science education is harmonized as a feature of the educational environment in a country. This interpretation is based on the premise that PISA measures students’ competence as educational outcomes (OECD [ 2004 ]). The operationalization of math-science coherence is realized by means of the correlation between math and science scores [ r (M,S)] at the country level. Low math-science coherence indicates that students who are successful in the acquisition of knowledge and skills in math are not necessarily successful in the acquisition of knowledge and skills in science and vice versa.
On the basis of this conceptualization of math-science coherence, we expect a significant and positive relation to problem solving scores, since the conceptual overlap between mathematical and scientific literacy refers to cognitive abilities such as reasoning and information processing that are also required in problem solving (Arts et al. [ 2006 ]; Beckmann [ 2001 ]; Wüstenberg et al. [ 2012 ]). Hence, we assert that math-science coherence facilitates the transfer of knowledge, skills, and insights across subjects resulting in better problem solving performance (OECD [ 2004 ]; Pellegrino and Hilton [ 2012 ]).
We also assume that math-science coherence as well as capability utilisation is linked to characteristics of the educational system of a country. For instance, as Janssen and Geiser ([ 2012 ]) and Blömeke et al. ([ 2011 ]) suggested, the developmental status of a country, measured by the Human Development Index (HDI; UNDP [ 2005 ]), is positively related to students’ academic achievements as well as to teachers’ quality of teaching. Furthermore, the socio-economic status of a country co-determines characteristics of its educational system, which ultimately affects a construct referred to as national intelligence (Lynn and Meisenberg [ 2010 ]). Research also indicated that curricular settings and educational objectives are related to school achievement in general (Bulle [ 2011 ]; Martin et al. [ 2004 ]). Besides these factors, school- and classroom-related characteristics might also confound the relation between math-science coherence and problem solving. For instance, the schools’ autonomy in developing curricula and managing educational resources might facilitate the incorporation of inquiry- and problem-based activities in science lessons (Chiu and Chow [ 2011 ]). These factors have been discussed as being influential to students’ competence development (OECD [ 2004 ], [ 2005 ]). Ewell ([ 2012 ]) implies that cross-national differences in problem solving competence might be related to differences in education and in using appropriate teaching material. These factors potentially confound the relation between math-science coherence and problem solving.
Discrepancies between math and problem solving scores are discussed in relation to quality of education. Although research has found that crossing the borders between STEM subjects positively affects students’ STEM competences (e.g., National Research Council NRC [ 2011 ]), we argue that the PISA analyses have fallen short in explaining cross-country differences in the development of problem solving competence, since they ignored the link between math and science competences and the synergistic effect of learning universally applicable problem-solving skills in diverse subject areas. Hence, we use the concept of math-science coherence to provide a more detailed description of the discrepancies between problem solving and domain-specific competences. In this regard, we argue that the coherence concept indicates the synergistic potential and students’ problem-solving competence the success of transfer.
The present study
The current study is based on the premise that in contrast to math and science competence problem solving competence is not explicitly taught as a subject at school. Problem solving competence, however, is an expected outcome of education (van Merriënboer [ 2013 ]). With the first step in our analyses, we seek to establish whether math and science education are in fact main contributors to the acquisition of problem solving competence. On the basis of this regression hypothesis, we subsequently focus on the question whether there are significant and systematic differences between countries ( Moderation-Hypothesis ). In light of the conceptual overlap due to cognitive processes involved in dealing with math, science and problem solving tasks and the shared item format employed in the assessments, we expect math and science competence scores to substantially predict scores in problem solving competence. Furthermore, since math and science education are differently organized across the 41 countries participating in the PISA 2003 study, differences in the contribution are also expected.
On the basis of these premises, we introduce the concept of math-science coherence, operationalised as the correlation between math and science scores [ r (M,S)], and analyse its relationship to problem solving and the effects of confounders (i.e., country characteristics) as a step of validation. Since math, science, and problem solving competence show a conceptual overlap, we expect problem solving and math-science coherence to be positively related. Countries’ educational systems differ in numerous aspects, their educational structure, and their educational objectives. Countries also differ with regard to the frequency of assessments, the autonomy of schools in setting up curricula and resources, and the educational resources available. Consequently, we expect the relation between math-science coherence and problem solving competence to be confounded by society-, curriculum-, and school-related factors ( Confounding-Hypothesis ).
In a final step, we aim to better understand the mechanisms with which math and science education contributes to the acquisition of problem-solving competence by exploring how math-science coherence, capability utilisation, and problem solving competence are related. We thus provide new insights into factors related to the transfer between students’ domain-specific and cross-curricular knowledge and skills ( Capability-Utilisation Hypothesis ).
In PISA 2003, a total sample of N = 276,165 students (49.4% female) from 41 countries participated. The entire sample was randomly selected by applying a two-step sampling procedure: First, schools were chosen within a country. Second, students were chosen within these schools. This procedure consequently led to a clustered structure of the data set, as students were nested in 10,175 schools. On average, 27 students per school were chosen across schools within countries. Students’ mean age was 15.80 years ( SD = 0.29 years) ranging from 15.17 to 16.25 years.
In the PISA 2003 study, different assessments were used in order to measure students’ competence in math, science, and problem solving. These assessments were administered as paper-and-pencil tests within a multi-matrix design (OECD [ 2005 ]). In this section, the assessments and further constructs are described that served as predictors of the contribution of math and science competence to problem solving at the country level.
Student achievement in math, science, and problem solving
In order to assess students’ competence to solve cross-curricular problems (i.e., analytical problem solving requiring information retrieval and reasoning), students had to work on an analytical problem-solving test. This test comprised a total of 19 items (7 items referred to trouble-shooting, 7 items referred to decision-making, and 5 items referred to system analysis and design; see OECD [ 2004 ]). Items were coded according to the PISA coding scheme, resulting in dichotomous and polytomous scores (OECD [ 2005 ]). Based on these scores, models of item response theory were specified in order to obtain person and item parameters (Leutner et al. [ 2012 ]). The resulting plausible values could be regarded as valid indicators of students’ abilities in problem solving (Wu [ 2005 ]). The problem solving test showed sufficient reliabilities between .71 and .89 for the 41 countries.
To assess mathematical literacy as an indicator of math competence , an 85-items test was administered (for details, refer to OECD [ 2003 ]). Responses were dichotomously or polytomously scored. Again, plausible values were obtained as person ability estimates and reliabilities were good (range: 0.83 – 0.93). In the context of mathematical literacy, students were asked to solve real-world problems by applying appropriate mathematical models. They were prompted to “identify and understand the role mathematics plays in the world, to make well-founded judgements and to use […] mathematics […]” (OECD [ 2003 ], p. 24).
Scientific literacy as a proxy for science competence was assessed by using problems referring to different content areas of science in life, health, and technology. The reliability estimates for the 35 items in this test ranged between .68 and .88. Again, plausible values served as indicators of this competence.
Country-specific characteristics
In our analyses, we incorporated a range of country-specific characteristics that can be subdivided into three main categories. These are: society-related factors, curriculum-related factors, and school-related factors. Country-specific estimates of National Intelligence as derived by Lynn and Meisenberg ([ 2010 ]) as well as the Human Development Index (HDI) were subsumed under society-related factors . The HDI incorporates indicators of a country’s health, education, and living standards (UNDP [ 2005 ]). Both variables are conceptualised as factors that contribute to country-specific differences in academic performance.
Holliday and Holliday ([ 2003 ]) emphasised the role of curricular differences in the understanding of between-country variance in test scores. We incorporated two curriculum-related factors in our analyses. First, we used Bulle’s ([ 2011 ]) classification of curricula into ‘progressive’ and ‘academic’. Bulle ([ 2011 ]) proposed this framework and classified the PISA 2003 countries according to their educational model. In her framework, she distinguishes between ‘academic models’ which are primarily geared towards teaching academic subjects (e.g., Latin, Germanic, and East-Asian countries) and ‘progressive models’ which focus on teaching students’ general competence in diverse contexts (e.g., Anglo-Saxon and Northern countries). In this regard, academic skills refer to the abilities of solving academic-type problems, whereas so called progressive skills are needed in solving real-life problems (Bulle [ 2011 ]). It can be assumed that educational systems that focus on fostering real-life and domain-general competence might be more conducive to successfully tackling the kind of problem solving tasks used in PISA (Kind [ 2013 ]). This classification of educational systems should be seen as the two extreme poles of a continuum rather than as a strict dichotomy. In line with the reflections above, we would argue that academic and progressive skills are not exclusively distinct, since both skills utilise sets of cognitive processes that largely overlap (Klahr and Dunbar [ 1988 ]). The fact that curricular objectives in some countries are shifting (e.g., in Eastern Asia) makes a clear distinction between both models even more difficult. Nonetheless, we will use this form of country-specific categorization based on Bulle’s model in our analyses.
Second, we considered whether countries’ science curricula were ‘integrated’ or ‘not integrated’ (Martin et al. [ 2004 ]). In this context, integration refers to linking multiple science subjects (biology, chemistry, earth science, and physics) to a unifying theme or issue (cf. Drake and Reid [ 2010 ], p. 1).
In terms of school-related factors, we used the PISA 2003 scales of ‘Frequency of assessments in schools’, ‘Schools’ educational resources’, and ‘School autonomy towards resources and curricula’ from the school questionnaire. Based on frequency and rating scales, weighted maximum likelihood estimates (WLE) indicated the degree to which schools performed in these scales (OECD [ 2005 ]).
The country-specific characteristics are summarized in the Table 1 .
The PISA 2003 assessments utilised a randomized incomplete block design to select different test booklets which covered the different content areas of math, science, and problem solving (Brunner et al. [ 2013 ]; OECD [ 2005 ]). The test administration took 120 minutes, and was managed for each participating country separately. It was established that quality standards of the assessment procedure were high.
Statistical analyses
In PISA 2003, different methods of obtaining person estimates with precise standard errors were applied. The most accurate procedure produced five plausible values, which were drawn from a person ability distribution (OECD [ 2005 ]). To avoid missing values in these parameters and to obtain accurate estimates, further background variables were used within the algorithms (Wu [ 2005 ]). The resulting plausible values were subsequently used as indicators of students’ competence in math, science, and problem solving. By applying Rubin’s combination rules (Bouhilila and Sellaouti [ 2013 ]; Enders [ 2010 ]), analyses were replicated with each of the five plausible values and then combined. In this multiple imputation procedure, standard errors were decomposed to the variability across and within the five imputations (Enders [ 2010 ]; OECD [ 2005 ]; Wu [ 2005 ]).
Within the multilevel regression analyses for each country, we specified the student level as level 1 and the school level as level 2. Since PISA 2003 applied a random sampling procedure at the student and the school level, we decided to control for the clustering of data at these two levels (OECD [ 2005 ]). In addition to this two-level procedure, we regarded the 41 countries as multiple groups (fixed effects). This decision was based on our assumption that the countries selected in PISA 2003 did not necessarily represent a sample of a larger population (Martin et al. [ 2012 ]). Moreover, we did not regard the effects of countries as interchangeable, because, given the specific characteristics of education and instruction within countries; we argue that the effects of competences in mathematics and science on problem solving have their own distinct interpretation in each country (Snijders and Bosker [ 2012 ]). The resulting models were compared by taking into account the Akaike’s information criteria ( AIC ), Bayesian information criteria ( BIC ), and the sample-size adjusted BIC . Also, a likelihood ratio test of the log-Likelihood values ( LogL ) was applied (Hox [ 2010 ]).
To test the Moderation-Hypothesis, we first specified a two-level regression model with problem solving scores as outcomes at the student level (level 1), which allowed variance in achievement scores across schools (level 2). In this model, math and science scores predicted problem solving scores at the student level. To account for differences in the probabilities of being selected as a student within the 41 countries and to adjust the standard errors of regression parameters, we used the robust maximum likelihood (MLR) estimator and students’ final weights (see also Brunner et al. [ 2013 ]; OECD [ 2005 ]). All analyses were conducted in Mplus 6.0 by using the TYPE = IMPUTATION option (Muthén and Muthén [ 2010 ]). As Hox ([ 2010 ]) suggested, using multilevel regression models without taking into account the clustering of data in schools often leads to biased estimates, since achievement variables often have substantial variance at the school level. Consequently, we allowed for level-2-variance within the scores.
After having established whether success in math and science education contributes to the development in problem solving competence across the 41 countries, we then tested whether cross-country differences in the unstandardized regression coefficients were statistically significant by using a multi-group regression model, in which the coefficients were constrained to be equal across countries. We compared this model with the freely estimated model.
Finally, we conceptualized the correlation between math and science scores as an indicator of the level of coherence in math and science education in a country. In relation to the Confounding-Hypothesis, we tested country-specific characteristics for their potentially confounding effects on the relation between math-science coherence and problem solving competence. Following the recommendations proposed by (MacKinnon et al. [ 2000 ]), the confounding analysis was conducted in two steps: (1) we estimated two regression equations. In the first equation, problem solving scores across the 41 countries were regressed on math-science coherence. In the second equation, the respective country characteristics were added as further predictors; (2) the difference between the regression coefficients for math-science coherence obtained in either equation represented the magnitude of a potential confounder effect.
Lastly, we tested the Capability-Utilisation Hypothesis by investigating the bivariate correlations among the CUU Indices and math-science coherence.
Regressing problem solving on math and science performance
To test the Moderation-Hypothesis, we specified regression models with students’ problem-solving score as the outcome and math and science scores as predictors for each of the 41 countries. Due to the clustering of data in schools, these models allowed for between-level variance. Intraclass correlations (ICC-1) for math, science, and problem solving performance ranged between .03 and .61 for the school level ( M = .33, SD = .16).
We specified multilevel regression models for each country separately. These results are reported in Table 2 . The regression coefficients for math on problem solving ranged from .53 to .82 with an average of M( β Math ) = .67 ( SD = .06). The average contribution of science towards problem solving was M( β Science ) = .16 ( SD = .09, Min = -.06, Max = .30). The combination of the distributions of both parameters resulted in substantial differences in the variance explanations of the problem solving scores across the 41 countries ( M[R 2 ] = .65, SD = .15, Min = .27, Max = .86). To test whether these differences were statistically significant, we constrained the regression coefficients of math and science competence within the multi-group regression model to be equal across the 41 countries. Compared to the freely estimated model ( LogL = -4,561,273.3, df = 492, AIC = 9,123,530.5, BIC = 9,128,410.7), the restricted model was empirically not preferred LogL = -4,564,877.9, df = 412, AIC = 9,130,579.8, BIC = 9,134,917.6; Δχ 2 [80] = 7,209.2, p < .001. These findings lend evidence for the Moderation-Hypothesis.
From a slightly different perspective, the country-specific amount of variance in problem solving scores that is explained by the variation in math and science performance scores ( R 2 ) is strongly associated with the country’s problem solving score ( r = .77, p < .001), which suggests that the contribution of science and math competence to the acquisition of problem solving competence was significantly lower in low-performing countries.
As shown in Table 2 , the regression weights of math and science were significant for all but two countries. Across countries the regression weight for math tended to be higher than the regression weight for science when predicting problem solving competence. This finding indicates a stronger overlap between students’ competences in mathematics and problem solving on the one hand and similarities between the assessments in both domains on the other hand.
Validating the concept of math-science coherence
In order to validate the concept of math-science coherence, which is operationalised as the correlation between math and science scores [ r (M,S)], we explored its relation to problem solving and country characteristics.
Regarding the regression outcomes shown in Table 2 , it is apparent that math-science coherence varied considerably across countries, ranging from .39 to .88 with an average of M(r) = .70 ( SD = .13). Interestingly, countries’ level of coherence in math-science education was substantially related to their problem solving scores ( r = .76, p < .001). An inspection of Figure 1 reveals that this effect was mainly due to countries that both achieve low problem solving scores and show relatively low levels of math-science coherence (see bottom left quadrant in Figure 1 ), whilst amongst the remaining countries the correlational link between math-science coherence and problem solving score was almost zero ( r = -.08, p = .71) b . This pattern extends the moderation perspective on the presumed dependency of problem solving competence from math and science competences.
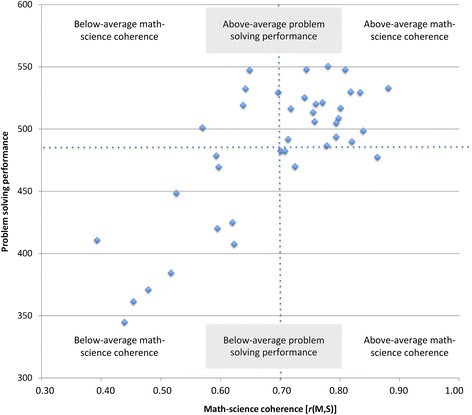
The relation between math-science coherence and problem solving performance across the 41 countries.
As a result of the moderator analysis, we know that countries not only differ in regard to their average problem-solving scores and level of coherence between math and science, countries also differ in the strengths with which math-science coherence predicts problem solving scores. To better understand the conceptual nature of the link between math-science coherence and problem solving, we now attempt to adjust this relationship for potential confounding effects that country-specific characteristics might have. To this end, we employed linear regression and path analysis with students’ problem-solving scores as outcomes, math-science coherence (i.e., r [M,S]) as predictor, and country characteristics as potential confounders.
To establish whether any of the country characteristics had a confounding effect on the link between math-science coherence and problem solving competence, two criteria had to be met: (1) a reduction of the direct effect of math-science coherence on problem solving scores, and (2) testing the difference between the direct effect within the baseline Model M0 and the effect with the confounding Model M1 (Table 3 ).
Regarding the society-related factors, both the countries’ HDI and their national intelligence were confounders with a positive effect. Furthermore, the countries’ integration of the science curriculum was also positively related to the problem solving performance. Finally, the degree of schools’ autonomy towards educational resources and the implementation of curricula and the frequency of assessments were school-related confounders, the former with a positive effect whilst the latter represents a negative confounder. The direct effect of math-science coherence to problem solving decreased and thus indicated that confounding was present (MacKinnon et al. [ 2000 ]).
These findings provide evidence on the Confounding-Hypothesis and support our expectations on the relation between math-science coherence, problem solving, and country characteristics. We regard these results as evidence for the validity of the math-science coherence measure.
Relating math-science coherence to the capability under-utilisation indices
To advance our understanding of the link between math-science coherence and problem solving scores, we tested the Capability-Utilisation Hypothesis. To this end, we explored the relationship between math-science coherence and the CUU Indices for math and science, respectively. For math competence the average Capability Under-Utilisation Index was rather neutral with M CUUI-Math = -0.001 ( SD = 0.02). This suggests that, on average, all countries sufficiently utilise their students’ math capabilities in facilitating the development of problem solving competence (i.e., transfer). It also suggests that math education across participating countries tends to sufficiently utilise generic problem-solving skills (Figure 2 ). The picture is different for science education. Here, the Capability Under-Utilisation Indices and their variation across the participating countries ( M CUUI-Science = -0.01, SD = 0.04) suggest that in a range of countries knowledge and skills taught in science education tend to be under-utilised in the facilitation of the acquisition of problem solving competence (Figure 3 ).
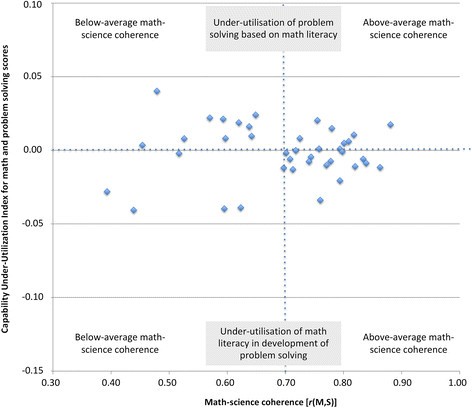
The relation between math-science coherence and the capability under-utilisation index for math and problem solving scores across the 41 countries.
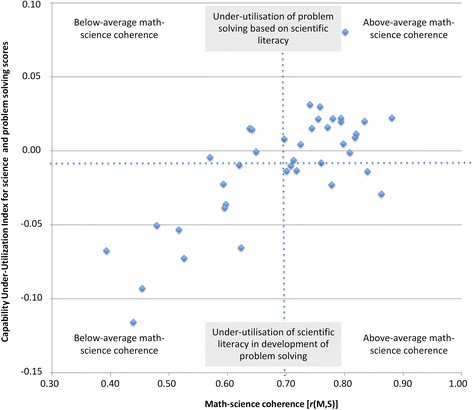
The relation between math-science coherence and the capability under-utilisation index for science and problem solving scores across the 41 countries.
For math competence, the relative difference to problem solving was not related to math-science coherence ( r = .02, p = .89; Figure 2 ). In contrast, the Capability Under-Utilisation Index for science showed a strong positive correlation with math-science coherence ( r = .76, p < .001; Figure 3 ), indicating that low levels of coherence between math and science education were associated with a less effective transfer of domain-specific knowledge and skills to problem solving.
The present study was aimed at investigating the differences in the contribution of math and science competence to problem solving competence across the 41 countries that participated in the PISA 2003 study (Moderation-Hypothesis). To this end, we proposed the concept of math-science coherence and explored its relationship to problem solving competence and how this relationship is confounded by country characteristics (Confounding-Hypothesis). To further extend our understanding of the link between math-science coherence and problem solving, we introduced the concept of capability-utilisation. Testing the Capability-Utilisation Hypothesis enabled us to identify what may contribute to varying levels of math-science coherence and ultimately the development of problem solving competence.
The contribution of math and science competence across countries
Regarding the prediction of problem solving competence, we found that in most countries, math and science competence significantly contributed to students’ performance in analytical problem solving. This finding was expected based on the conceptualizations of mathematical and scientific literacy within the PISA framework referring to shared cognitive processes such as information processing and reasoning (Kind [ 2013 ]; OECD [ 2005 ]), which are regarded as components of problem solving (Bybee [ 2004 ]; Klahr and Dunbar [ 1988 ]; Mayer [ 2010 ]).
It is noteworthy that, for some of the below-average performing countries, science competence did not significantly contribute to the prediction of problem solving competence. It can be speculated that education in these countries is more geared towards math education and modelling processes in mathematical scenarios, whilst the aspect of problem solving in science is less emphasised (Janssen and Geiser [ 2012 ]). The results of multilevel regression analyses supported this interpretation by showing that math competence was a stronger predictor of problem solving competence. On the one hand, this finding could be due to the design of the PISA tests (Adams [ 2005 ]), since math and problem solving items are designed in such a way that modelling real-life problems is required, whereas science items are mostly domain-specific and linked to science knowledge (Nentwig et al. [ 2009 ]; OECD [ 2004 ]). Moreover, one may argue that math and problem solving items allow students to employ different solution strategies, whereas science items offer fewer degrees of freedom for test takers (Nentwig et al. [ 2009 ]). In particular, the shared format of items in math, science, and problem solving may explain an overlap between their cognitive demands. For instance, most of the items were designed in such a way that students had to extract and identify relevant information from given tables or figures in order to solve specific problems. Hence, these items were static and did not require knowledge generation by interaction or exploration but rather the use of given information in problem situations (Wood et al. [ 2009 ]). In contrast to the domain-specific items in math and science, problem solving items did not require the use of prior knowledge in math and science (OECD [ 2004 ]). In addition, some of the math and science items involved cognitive operations that were specific to these domains. For instance, students had to solve a number of math items by applying arithmetic and combinatorial operations (OECD [ 2005 ]). Finally, since items referred to contextual stimuli, which were presented in textual formats, reading ability can be regarded as another, shared demand of solving the items. Furthermore, Rindermann ([ 2007 ]) clearly showed that the shared demands of the achievement tests in large-scale assessments such as PISA were strongly related to students’ general reasoning skills. This finding is in line with the strong relations between math, science, and problem solving competence, found in our study. The interpretation of the overlap between the three competences can also be interpreted from a conceptual point of view. In light of the competence frameworks in PISA, we argue that there are a number of skills that can be found in math, science, and problem solving: information retrieval and processing, knowledge application, and evaluation of results (Griffin et al. [ 2012 ]; OECD [ 2004 ], [ 2005 ]). These skills point out to the importance of reasoning in the three domains (Rindermann [ 2007 ]). Thus, the empirical overlap between math and problem solving can be explained by shared processes of, what Mayer ([ 2010 ]) refers to as, informal reasoning. On the other hand, the stronger effect of math competence could be an effect of the quality of math education. Hiebert et al. ([ 1996 ]) and Kuo et al. ([ 2013 ]) suggested that math education is more based on problem solving skills than other subjects in school (e.g., Polya [ 1945 ]). Science lessons, in contrast, are often not necessarily problem-based, despite the fact that they often start with a set problem. Risch ([ 2010 ]) showed in a cross-national review that science learning was more related to contents and contexts rather than to generic problem-solving skills. These tendencies might lead to a weaker contribution of science education to the development of problem solving competence (Abd-El-Khalick et al. [ 2004 ]).
In sum, we found support on the Moderation-Hypothesis, which assumed systematic differences in the contribution of math and science competence to problem solving competence across the 41 PISA 2003 countries.
The relation to problem solving
In our study, we introduced the concept of math-science coherence, which reflects the degree to which math and science education are harmonized. Since mathematical and scientific literacy show a conceptual overlap, which refers to a set of cognitive processes that are linked to reasoning and information processing (Fensham and Bellocchi [ 2013 ]; Mayer [ 2010 ]), a significant relation between math-science coherence and problem solving was expected. In our analyses, we found a significant and positive effect of math-science coherence on performance scores in problem solving. In this finding we see evidence for the validity of this newly introduced concept of math-science coherence and its focus on the synergistic effect of math and science education on problem solving. The results further suggest that higher levels of coordination between math and science education has beneficial effects on the development of cross-curricular problem-solving competence (as measured within the PISA framework).
Confounding effects of country characteristics
As another step of validating the concept of math-science coherence, we investigated whether country-specific characteristics that are linked to society-, curriculum-, and school-related factors confounded its relation to problem solving. Our results showed that national intelligence, the Human Development Index, the integration of the science curriculum, and schools’ autonomy were positively linked to math-science coherence and problem solving, whilst a schools’ frequency of assessment had a negative confounding effect.
The findings regarding the positive confounders are in line with and also extend a number of studies on cross-country differences in education (e.g., Blömeke et al. [ 2011 ]; Dronkers et al. [ 2014 ]; Janssen and Geiser [ 2012 ]; Risch [ 2010 ]). Ross and Hogaboam-Gray ([ 1998 ]), for instance, found that students benefit from an integrated curriculum, particularly in terms of motivation and the development of their abilities. In the context of our confounder analysis, the integration of the science curriculum as well as the autonomy to allocate resources is expected to positively affect math-science coherence. At the same time, an integrated science curriculum with a coordinated allocation of resources may promote inquiry-based experiments in science courses, which is assumed to be beneficial for the development of problem solving within and across domains. Teaching science as an integrated subject is often regarded a challenge for teachers, particularly when developing conceptual structures in science lessons (Lang and Olson, [ 2000 ]), leading to teaching practices in which cross-curricular competence is rarely taken into account (Mansour [ 2013 ]; van Merriënboer [ 2013 ]).
The negative confounding effect of assessment frequency suggests that high frequencies of assessment, as it presumably applies to both math and science subjects, contribute positively to math-science coherence. However, the intended or unintended engagement in educational activities associated with assessment preparation tends not to be conducive to effectively developing domain-general problem solving competence (see also Neumann et al. [ 2012 ]).
The positive confounder effect of HDI is not surprising as HDI reflects a country’s capability to distribute resources and to enable certain levels of autonomy (Reich et al. [ 2013 ]). To find national intelligence as a positive confounder is also to be expected as the basis for its estimation are often students’ educational outcome measures (e.g., Rindermann [ 2008 ]) and, as discussed earlier, academic achievement measures share the involvement of a set of cognitive processes (Baumert et al. [ 2009 ]; OECD [ 2004 ]).
In summary, the synergistic effect of a coherent math and science education on the development of problem solving competence is substantially linked to characteristics of a country’s educational system with respect to curricula and school organization in the context of its socio-economic capabilities. Math-science coherence, however, also is linked to the extent to which math or science education is able to utilise students’ educational capabilities.
Math-science coherence and capability-utilisation
So far, discrepancies between students’ performance in math and problem solving or science and problem solving have been discussed as indicators of students’ capability utilisation in math or science (Leutner et al. [ 2012 ]; OECD [ 2004 ]). We have extended this perspective by introducing Capability Under-Utilisation Indices for math and science to investigate the effectiveness with which knowledge and skills acquired in the context of math or science education are transferred into cross-curricular problem-solving competence. The Capability Under-Utilisation Indices for math and science reflect a potential quantitative imbalance between math, science, and problem solving performance within a country, whilst the also introduced concept of math-science coherence reflects a potential qualitative imbalance between math and science education.
The results of our analyses suggest that an under-utilisation of problem solving capabilities in the acquisition of science literacy is linked to lower levels of math-science coherence, which ultimately leads to lower scores in problem solving competence. This interpretation finds resonance in Ross and Hogaboam-Gray’s ([ 1998 ]) argumentation for integrating math and science education and supports the attempts of math and science educators to incorporate higher-order thinking skills in teaching STEM subjects (e.g., Gallagher et al. [ 2012 ]; Zohar [ 2013 ]).
In contrast, the CUU Index for math was not related to math-science coherence in our analyses. This might be due to the conceptualizations and assessments of mathematical literacy and problem solving competence. Both constructs share cognitive processes of reasoning and information processing, resulting in quite similar items. Consequently, the transfer from math-related knowledge and skills to cross-curricular problems does not necessarily depend on how math and science education are harmonised, since the conceptual and operational discrepancy between math and problem solving is rather small.
Math and science education do matter to the development of students’ problem-solving skills. This argumentation is based on the assumption that the PISA assessments in math, science, and problem solving are able to measure students’ competence as outcomes, which are directly linked to their education (Bulle [ 2011 ]; Kind [ 2013 ]). In contrast to math and science competence, problem solving competence is not explicitly taught as a subject. Problem solving competence requires the utilisation of knowledge and reasoning skills acquired in specific domains (Pellegrino and Hilton [ 2012 ]). In agreement with Kuhn ([ 2009 ]), we point out that this transfer does not happen automatically but needs to be actively facilitated. In fact, Mayer and Wittrock ([ 2006 ]) stressed that the development of transferable skills such as problem solving competence needs to be fostered within specific domains rather than taught in dedicated, distinct courses. Moreover, they suggested that students should develop a “repertoire of cognitive and metacognitive strategies that can be applied in specific problem-solving situations” (p. 299). Beyond this domain-specific teaching principle, research also proposes to train the transfer of problem solving competence in domains that are closely related (e.g., math and science; Pellegrino and Hilton [ 2012 ]). In light of the effects of aligned curricula (as represented by the concept of math-science coherence), we argue that educational efforts to increase students’ problem solving competence may focus on a coordinated improvement of math and science literacy and fostering problem solving competence within math and science. The emphasis is on coordinated, as the results of our analyses indicated that the coherence between math and science education, as a qualitative characteristic of a country’s educational system, is a strong predictor of problem solving competence. This harmonisation of math and science education may be achieved by better enabling the utilisation of capabilities, especially in science education. Sufficiently high levels of math-science coherence could facilitate the emergence of educational synergisms, which positively affect the development of problem solving competence. In other words, we argue for quantitative changes (i.e., improve science attainment) in order to achieve qualitative changes (i.e., higher levels of curriculum coherence), which are expected to create effective transitions of subject-specific knowledge and skills into subject-unspecific competences to solve real-life problems (Pellegrino and Hilton [ 2012 ]; van Merriënboer [ 2013 ]).
Finally, we encourage research that is concerned with the validation of the proposed indices for different forms of problem solving. In particular, we suggest studying the facilities of the capability-under-utilisation indices for analytical and dynamic problem solving, as assessed in the PISA 2012 study (OECD [ 2014 ]). Due to the different cognitive demands in analytical and dynamic problems (e.g., using existing knowledge vs. generating knowledge; OECD [ 2014 ]), we suspect differences in capability utilisation in math and science. This research could provide further insights into the role of 21 st century skills as educational goals.
a The differences between students’ achievement in mathematics and problem solving, and science and problem solving have to be interpreted relative to the OECD average, since the achievement scales were scaled with a mean of 500 and a standard deviation of 100 for the OECD countries (OECD [ 2004 ], p. 55). Although alternative indices such as country residuals may also be used in cross-country comparisons (e.g., Olsen [ 2005 ]), we decided to use CUU indices, as they reflect the actual differences in achievement scores.
b In addition, we checked whether this result was due to the restricted variances in low-performing countries and found that neither ceiling nor floor effects in the problem solving scores existed. The problem solving scale differentiated sufficiently reliably in the regions below and above the OECD mean of 500.
Abd-El-Khalick F, Boujaoude S, Duschl R, Lederman NG, Mamlok-Naaman R, Hofstein A, Niaz M, Treagust D, Tuan H-L: Inquiry in science education: International perspectives. Science Education 2004, 88: 397–419. doi:10.1002/sce.10118 10.1002/sce.10118
Article Google Scholar
Adams RJ: Reliability as a measurement design effect. Studies in Educational Evaluation 2005, 31: 162–172. doi:10.1016/j.stueduc.2005.05.008 10.1016/j.stueduc.2005.05.008
Arts J, Gijselaers W, Boshuizen H: Understanding managerial problem solving, knowledge use and information processing: Investigating stages from school to the workplace. Contemporary Educational Psychology 2006, 31: 387–410. doi:10.1016/j.cedpsych.2006.05.005 10.1016/j.cedpsych.2006.05.005
Bassok M, Holyoak K: Pragmatic knowledge and conceptual structure: determinants of transfer between quantitative domains. In Transfer on trial: intelligence, cognition, and instruction . Edited by: Detterman DK, Sternberg RJ. Ablex, Norwood, NJ; 1993:68–98.
Google Scholar
Baumert J, Lüdtke O, Trautwein U, Brunner M: Large-scale student assessment studies measure the results of processes of knowledge acquisition: evidence in support of the distinction between intelligence and student achievement. Educational Research Review 2009, 4: 165–176. doi:10.1016/j.edurev.2009.04.002 10.1016/j.edurev.2009.04.002
Beckmann JF: Zur Validierung des Konstrukts des intellektuellen Veränderungspotentials [On the validation of the construct of intellectual change potential] . logos, Berlin; 2001.
Blömeke S, Houang R, Suhl U: TEDS-M: diagnosing teacher knowledge by applying multidimensional item response theory and multiple-group models. IERI Monograph Series: Issues and Methodologies in Large-Scale Assessments 2011, 4: 109–129.
Bouhilila D, Sellaouti F: Multiple imputation using chained equations for missing data in TIMSS: a case study. Large-scale Assessments in Education 2013, 1: 4.
Brunner M, Gogol K, Sonnleitner P, Keller U, Krauss S, Preckel F: Gender differences in the mean level, variability, and profile shape of student achievement: Results from 41 countries. Intelligence 2013, 41: 378–395. doi:10.1016/j.intell.2013.05.009 10.1016/j.intell.2013.05.009
Bulle N: Comparing OECD educational models through the prism of PISA. Comparative Education 2011, 47: 503–521. doi: 10.1080/03050068.2011.555117 10.1080/03050068.2011.555117
Bybee R: Scientific Inquiry and Science Teaching. In Scientific Inquiry and the Nature of Science . Edited by: Flick L, Lederman N. Springer & Kluwers, New York, NY; 2004:1–14. doi:10.1007/978–1-4020–5814–1_1
Chiu M, Chow B: Classroom discipline across forty-One countries: school, economic, and cultural differences. Journal of Cross-Cultural Psychology 2011, 42: 516–533. doi:10.1177/0022022110381115 10.1177/0022022110381115
Drake S, Reid J: Integrated curriculum: Increasing relevance while maintaining accountability. Research into Practice 2010, 28: 1–4.
Dronkers J, Levels M, de Heus M: Migrant pupils’ scientific performance: the influence of educational system features of origin and destination countries. Large-scale Assessments in Education 2014, 2: 3.
Enders C: Applied Missing Data Analysis . The Guilford Press, New York, NY; 2010.
Ewell P: A world of assessment: OECD’s AHELO initiative. Change: The Magazine of Higher Learning 2012, 44: 35–42. doi:10.1080/00091383.2012.706515 10.1080/00091383.2012.706515
Fensham P, Bellocchi A: Higher order thinking in chemistry curriculum and its assessment. Thinking Skills and Creativity 2013, 10: 250–264. doi:10.1016/j.tsc.2013.06.003 10.1016/j.tsc.2013.06.003
Gallagher C, Hipkins R, Zohar A: Positioning thinking within national curriculum and assessment systems: perspectives from Israel, New Zealand and Northern Ireland. Thinking Skills and Creativity 2012, 7: 134–143. doi:10.1016/j.tsc.2012.04.005 10.1016/j.tsc.2012.04.005
Greiff S, Holt D, Funke J: Perspectives on problem solving in educational assessment: analytical, interactive, and collaborative problem solving. The Journal of Problem Solving 2013, 5: 71–91. doi:10.7771/1932–6246.1153 10.7771/1932-6246.1153
Griffin P, Care E, McGaw B: The changing role of education and schools. In Assessment and Teaching of 21st Century Skills . Edited by: Griffin P, McGaw B, Care E. Springer, Dordrecht; 2012:1–15. 10.1007/978-94-007-2324-5_1
Chapter Google Scholar
Hickendorff M: The language factor in elementary mathematics assessments: Computational skills and applied problem solving in a multidimensional IRT framework. Applied Measurement in Education 2013, 26: 253–278. doi:10.1080/08957347.2013.824451 10.1080/08957347.2013.824451
Hiebert J, Carpenter T, Fennema E, Fuson K, Human P, Murray H, Olivier A, Wearne D: Problem Solving as a Basis for Reform in Curriculum and Instruction: The Case of Mathematics. Educational Researcher 1996, 25: 12–21. doi:10.3102/0013189X025004012 10.3102/0013189X025004012
Holliday W, Holliday B: Why using international comparative math and science achievement data from TIMSS is not helpful. The Educational Forum 2003, 67: 250–257. 10.1080/00131720309335038
Hox J: Multilevel Analysis . 2nd edition. Routlegde, New York, NY; 2010.
Janssen A, Geiser C: Cross-cultural differences in spatial abilities and solution strategies: An investigation in Cambodia and Germany. Journal of Cross-Cultural Psychology 2012, 43: 533–557. doi:10.1177/0022022111399646 10.1177/0022022111399646
Jonassen D: Learning to solve problems . Routledge, New York, NY; 2011.
Kind P: Establishing Assessment Scales Using a Novel Disciplinary Rationale for Scientific Reasoning. Journal of Research in Science Teaching 2013, 50: 530–560. doi:10.1002/tea.21086 10.1002/tea.21086
Klahr D, Dunbar K: Dual Space Search during Scientific Reasoning. Cognitive Science 1988, 12: 1–48. doi:10.1207/s15516709cog1201_1 10.1207/s15516709cog1201_1
Koeppen K, Hartig J, Klieme E, Leutner D: Current issues in competence modeling and assessment. Journal of Psychology 2008, 216: 61–73. doi:10.1027/0044–3409.216.2.61
Kuhn D: Do students need to be taught how to reason? Educational Research Review 2009, 4: 1–6. doi:10.1016/j.edurev.2008.11.001 10.1016/j.edurev.2008.11.001
Kuo E, Hull M, Gupta A, Elby A: How Students Blend Conceptual and Formal Mathematical Reasoning in Solving Physics Problems. Science Education 2013, 97: 32–57. doi:10.1002/sce.21043 10.1002/sce.21043
Lang M, Olson J: Integrated science teaching as a challenge for teachers to develop new conceptual structures. Research in Science Education 2000, 30: 213–224. doi:10.1007/BF02461629 10.1007/BF02461629
Leutner D, Fleischer J, Wirth J, Greiff S, Funke J: Analytische und dynamische Problemlösekompetenz im Lichte internationaler Schulleistungsstudien [Analytical and dynamic problem-solvng competence in international large-scale studies]. Psychologische Rundschau 2012, 63: 34–42. doi:10.1026/0033–3042/a000108 10.1026/0033-3042/a000108
Lynn R, Meisenberg G: National IQs calculated and validated for 108 nations. Intelligence 2010, 38: 353–360. doi:10.1016/j.intell.2010.04.007 10.1016/j.intell.2010.04.007
MacKinnon D, Krull J, Lockwood C: Equivalence of the mediation, confounding, and suppression effect. Prevention Science 2000, 1: 173–181. doi:10.1023/A:1026595011371 10.1023/A:1026595011371
Mansour N: Consistencies and inconsistencies between science teachers’ beliefs and practices. International Journal of Science Education 2013, 35: 1230–1275. doi:10.1080/09500693.2012.743196 10.1080/09500693.2012.743196
Martin M, Mullis I, Gonzalez E, Chrostowski S: TIMSS 2003 International Science Report . IEA, Chestnut Hill, MA; 2004.
Martin AJ, Liem GAD, Mok MMC, Xu J: Problem solving and immigrant student mathematics and science achievement: Multination findings from the Programme for International Student Assessment (PISA). Journal of Educational Psychology 2012, 104: 1054–1073. doi:10.1037/a0029152 10.1037/a0029152
Mayer R: Problem solving and reasoning. In International Encyclopedia of Education . 3rd edition. Edited by: Peterson P, Baker E, McGraw B. Elsevier, Oxford; 2010:273–278. doi:10.1016/B978–0-08–044894–7.00487–5 10.1016/B978-0-08-044894-7.00487-5
Mayer R, Wittrock MC: Problem solving. In Handbook of Educational Psychology . 2nd edition. Edited by: Alexander PA, Winne PH. Lawrence Erlbaum, New Jersey; 2006:287–303.
Muthén B, Muthén L: Mplus 6 . Muthén & Muthén, Los Angeles, CA; 2010.
Successful K-12 STEM Education . National Academies Press, Washington, DC; 2011.
Nentwig P, Rönnebeck S, Schöps K, Rumann S, Carstensen C: Performance and levels of contextualization in a selection of OECD countries in PISA 2006. Journal of Research in Science Teaching 2009, 8: 897–908. doi:10.1002/tea.20338 10.1002/tea.20338
Neumann K, Kauertz A, Fischer H: Quality of Instruction in Science Education. In Second International Handbook of Science Education (Part One . Edited by: Fraser B, Tobin K, McRobbie C. Springer, Dordrecht; 2012:247–258.
The PISA 2003 Assessment Frameworks . OECD, Paris; 2003.
Problem solving for tomorrow’s world . OECD, Paris; 2004.
PISA 2003 Technical Report . OECD, Paris; 2005.
PISA 2012 Results : Creative Problem Solving – Students’ Skills in Tackling Real-Life Problems (Vol. V) . OECD, Paris; 2014.
Olsen RV: An exploration of cluster structure in scientific literacy in PISA: Evidence for a Nordic dimension? NorDiNa. ᅟ 2005, 1 (1):81–94.
Oser F, Baeriswyl F: Choreographies of Teaching: Bridging Instruction to Learning. In Handbook of Research on Teaching . 4th edition. Edited by: Richardson V. American Educational Research Association, Washington, DC; 2001:1031–1065.
Pellegrino JW, Hilton ML: Education for Life and Work – Developing Transferable Knowledge and Skills in the 21st Century . The National Academies Press, Washington, DC; 2012.
Polya G: How to solve it: a new aspect of mathematical method . Princeton University Press, Princeton, NJ; 1945.
Reich J, Hein S, Krivulskaya S, Hart L, Gumkowski N, Grigorenko E: Associations between household responsibilities and academic competencies in the context of education accessibility in Zambia. Learning and Individual Differences 2013, 27: 250–257. doi:10.1016/j.lindif.2013.02.005 10.1016/j.lindif.2013.02.005
Rindermann H: The g-factor of international cognitive ability comparisons: The homogeneity of results in PISA, TIMSS, PIRLS and IQ-tests across nations. European Journal of Personality 2007, 21: 661–706. doi:10.1002/per.634
Rindermann H: Relevance of education and intelligence at the national level for the economic welfare of people. Intelligence 2008, 36: 127–142. doi:10.1016/j.intell.2007.02.002 10.1016/j.intell.2007.02.002
Risch B: Teaching Chemistry around the World . Waxmann, Münster; 2010.
Ross J, Hogaboam-Gray A: Integrating mathematics, science, and technology: effects on students. International Journal of Science Education 1998, 20: 1119–1135. doi:10.1080/0950069980200908 10.1080/0950069980200908
Snijders TAB, Bosker RJ: Multilevel Analysis: An Introduction to Basic and Advanced Multilevel Modeling . 2nd edition. Sage Publications, London; 2012.
Human Development Report 2005 . UNDP, New York, NY; 2005.
Van Merriënboer J: Perspectives on problem solving and instruction. Computers & Education 2013, 64: 153–160. doi:10.1016/j.compedu.2012.11.025 10.1016/j.compedu.2012.11.025
Wood RE, Beckmann JF, Birney D: Simulations, learning and real world capabilities. Education Training 2009, 51 (5/6):491–510. doi:10.1108/00400910910987273 10.1108/00400910910987273
Wu M: The role of plausible values in large-scale surveys. Studies in Educational Evaluation 2005, 31: 114–128. doi:10.1016/j.stueduc.2005.05.005 10.1016/j.stueduc.2005.05.005
Wu M, Adams R: Modelling Mathematics Problem Solving Item Responses using a Multidimensional IRT Model. Mathematics Education Research Journal 2006, 18: 93–113. doi:10.1007/BF03217438 10.1007/BF03217438
Wüstenberg S, Greiff S, Funke J: Complex problem solving: More than reasoning? Intelligence 2012, 40: 1–14. doi:10.1016/j.intell.2011.11.003 10.1016/j.intell.2011.11.003
Zohar A: Scaling up higher order thinking in science classrooms: the challenge of bridging the gap between theory, policy and practice. Thinking Skills and Creativity 2013, 10: 168–172. doi:10.1016/j.tsc.2013.08.001 10.1016/j.tsc.2013.08.001
Download references
Author information
Authors and affiliations.
Centre for Educational Measurement, University of Oslo (CEMO), Oslo, Norway
Ronny Scherer
Faculty of Educational Sciences, University of Oslo, Oslo, Norway
School of Education, Durham University, Durham, UK
Jens F Beckmann
You can also search for this author in PubMed Google Scholar
Corresponding author
Correspondence to Ronny Scherer .
Additional information
Competing interests.
The authors declare that they have no competing interests.
Authors’ contributions
RS carried out the analyses, participated in the development of the rationale, and drafted the manuscript. JFB carried out some additional analyses, participated in the development of the rationale, and drafted the manuscript. Both authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Authors’ original file for figure 1
Authors’ original file for figure 2, authors’ original file for figure 3, rights and permissions.
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License ( https://creativecommons.org/licenses/by/4.0 ), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Reprints and permissions
About this article
Cite this article.
Scherer, R., Beckmann, J.F. The acquisition of problem solving competence: evidence from 41 countries that math and science education matters. Large-scale Assess Educ 2 , 10 (2014). https://doi.org/10.1186/s40536-014-0010-7
Download citation
Received : 08 June 2014
Accepted : 25 November 2014
Published : 10 December 2014
DOI : https://doi.org/10.1186/s40536-014-0010-7
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Capability under-utilisation
- Math-science coherence
- Math education
- Problem solving competence
- Science education
An official website of the United States government
The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.
The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.
- Publications
- Account settings
Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .
- Advanced Search
- Journal List
- v.9(5); 2023 May
- PMC10208825

Development and differences in mathematical problem-solving skills: A cross-sectional study of differences in demographic backgrounds
Ijtihadi kamilia amalina.
a Doctoral School of Education, University of Szeged, Hungary
Tibor Vidákovich
b Institute of Education, University of Szeged, Hungary
Associated Data
Data will be made available on request.
Problem-solving skills are the most applicable cognitive tool in mathematics, and improving the problem-solving skills of students is a primary aim of education. However, teachers need to know the best period of development and the differences among students to determine the best teaching and learning methods. This study aims to investigate the development and differences in mathematical problem-solving skills of students based on their grades, gender, and school locations. A scenario-based mathematical essay test was administered to 1067 students in grades 7–9 from schools in east Java, Indonesia, and their scores were converted into a logit scale for statistical analysis. The results of a one-way analysis of variance and an independent sample t -test showed that the students had an average level of mathematical problem-solving skills. The number of students who failed increased with the problem-solving phase. The students showed development of problem-solving skills from grade 7 to grade 8 but not in grade 9. A similar pattern of development was observed in the subsample of urban students, both male and female. The demographic background had a significant effect, as students from urban schools outperformed students from rural schools, and female students outperformed male students. The development of problem-solving skills in each phase as well as the effects of the demographic background of the participants were thoroughly examined. Further studies are needed with participants of more varied backgrounds.
1. Introduction
Problem-solving skills are a complex set of cognitive, behavioral, and attitudinal components that are situational and dependent on thorough knowledge and experience [ 1 , 2 ]. Problem-solving skills are acquired over time and are the most widely applicable cognitive tool [ 3 ]. Problem-solving skills are particularly important in mathematics education [ 3 , 4 ]. The development of mathematical problem-solving skills can differ based on age, gender stereotypes, and school locations [ [5] , [6] , [7] , [8] , [9] , [10] ]. Fostering the development of mathematical problem-solving skills is a major goal of educational systems because they provide a tool for success [ 3 , 11 ]. Mathematical problem-solving skills are developed through explicit training and enriching materials [ 12 ]. Teachers must understand how student profiles influence the development of mathematical problem-solving skills to optimize their teaching methods.
Various studies on the development of mathematical problem-solving skills have yielded mixed results. Grissom [ 13 ] concluded that problem-solving skills were fixed and immutable. Meanwhile, other researchers argued that problem-solving skills developed over time and were modifiable, providing an opportunity for their enhancement through targeted educational intervention when problem-solving skills developed quickly [ 3 , 4 , 12 ]. Tracing the development of mathematical problem-solving skills is crucial. Further, the results of previous studies are debatable, necessitating a comprehensive study in the development of students’ mathematical problem-solving skills.
Differences in mathematical problem-solving skills have been identified based on gender and school location [ [6] , [7] , [8] , [9] , [10] ]. School location affects school segregation and school quality [ 9 , 14 ]. The socioeconomic and sociocultural characteristics of a residential area where a school is located are the factors affecting academic achievement [ 14 ]. Studies in several countries have shown that students in urban schools demonstrated better performance and problem-solving skills in mathematics [ 9 , 10 , 15 ]. However, contradictory results have been obtained for other countries [ 6 , 10 ].
Studies on gender differences have shown that male students outperform female students in mathematics, which has piqued the interest of psychologists, sociologists, and educators [ 7 , 16 , 17 ]. The differences appear to be because of brain structure; however, sociologists argue that gender equality can be achieved by providing equal educational opportunities [ 8 , 16 , 18 , 19 ]. Because the results are debatable and no studies on gender differences across grades in schools have been conducted, it would be interesting to investigate gender differences in mathematical problem-solving skills.
Based on the previous explanations, teachers need to understand the best time for students to develop mathematical problem-solving skills because problem-solving is an obligatory mathematics skill to be mastered. However, no relevant studies focused on Indonesia have been conducted regarding the mathematical problem-solving skill development of students in middle school that can provide the necessary information for teachers. Further, middle school is the important first phase of developing critical thinking skills; thus relevant studies are required in this case [ 3 , 4 ]. In addition, a municipal policy-making system can raise differences in problem-solving skills based on different demographic backgrounds [ 10 ]. Moreover, the results of previous studies regarding the development and differences in mathematical problem-solving skills are debatable. Thus, the present study has been conducted to meet these gaps. This study investigated the development of mathematical problem-solving skills in students and the differences owing demographic backgrounds. Three aspects were considered: (1) student profiles of mathematical problem-solving skills, (2) development of their mathematical problem-solving skills across grades, and (3) significant differences in mathematical problem-solving skills based on gender and school location. The results of the present study will provide detailed information regarding the subsample that contributes to the development of mathematical problem-solving skills in students based on their demographic backgrounds. In addition, the description of the score is in the form of a logit scale from large-scale data providing consistent meaning and confident generalization. This study can be used to determine appropriate teaching and learning in the best period of students’ development in mathematical problem-solving skills as well as policies to achieve educational equality.
2. Theoretical background
2.1. mathematical problem-solving skills and their development.
Solving mathematical problems is a complex cognitive ability that requires students to understand the problem as well as apply mathematical concepts to them [ 20 ]. Researchers have described the phases of solving a mathematical problem as understanding the problem, devising a plan, conducting out the plan, and looking back [ [20] , [24] , [21] , [22] , [23] ]. Because mathematical problems are complex, students may struggle with several phases, including applying mathematical knowledge, determining the concepts to use, and stating mathematical sentences (e.g., arithmetic) [ 20 ]. Studies have concluded that more students fail at later stages of the solution process [ 25 , 26 ]. In other words, fewer students fail in the phase of understanding a problem than during the plan implementation phase. Different studies have stated that students face difficulties in understanding the problem, determining what to assume, and investigating relevant information [ 27 ]. This makes them unable to translate the problem into a mathematical form.
Age or grade is viewed as one factor that influences mathematical problem-solving skills because the skills of the students improve over time as a result of the teaching and learning processes [ 28 ]. Neuroscience research has shown that older students have fewer problems with arithmetic than younger students; however, the hemispheric asymmetry is reduced [ 29 ]. In other words, older students are more proficient, but their flexibility to switch among different strategies is less. Ameer & Sigh [ 28 ] obtained similar results and found a considerable difference in mathematical achievement; specifically, older students performed better than younger students in number sense and computation using one-way analysis of variance (ANOVA) ( F ) of F (2,411) = 4.82, p < 0.01. Molnár et al. [ 3 ] found that the student grade affects domain-specific and complex problem-solving skills. They observed that the development of problem-solving skills was noticeable across grades in elementary school but stopped in secondary school. The fastest development of domain-specific problem-solving occurred in grades 7 and 8 [ 3 ], but the fastest development of complex problem-solving occurred in grades 5–7 [ 3 ]. No development was detected between grades 4 and 5 as well as grades 6 and 7 for domain-specific and complex problem-solving skills, respectively. Similarly, Greiff et al. [ 4 ] concluded that students developed problem-solving skills across grades 5–11 with older students being more skilled. However, the grade 9 students deviated from the development pattern, and their problem-solving skills dropped. The theories from Molnár et al. [ 3 ] and Greiff et al. [ 4 ] are the benchmark cases herein.
The above studies showed that problem-solving skills mostly developed during compulsory schooling and developed most quickly in specific grades. This indicates that specific development times can be targeted to enhance the problem-solving skills [ 3 ]. However, Jabor et al. [ 30 ] observed contradictory results showing statistically significant differences with small effects in mathematical performance between age groups: those under the age of 19 outperformed those over the age of 19 years old. Grissom [ 13 ] observed a negative correlation between age and school achievement that remained constant over time.
2.2. Effects of school location and gender on mathematical problem-solving skills
School location has been shown to affect mathematical achievement [ 9 , 14 ]. In 15 countries, students in rural schools performed considerably worse than students in urban schools in mathematics [ 9 , 10 ], science and reading [ 9 ]. In addition, Nepal [ 15 ] discovered that urban students significantly outperformed rural students in mathematical problem-solving skills ( t = −5.11, p < 0.001) and achievement ( t = −4.45, p < 0.001) using the results of an independent sample t -test (t). However, other countries have found that rural students outperformed urban students in mathematics [ 6 , 10 ]. These variations may be attributed to a lack of instructional resources (e.g., facilities, materials, and programs), professional training (e.g., poorly trained teachers), and progressive instruction [ 6 ]. The results of Williams's study [ 10 ] serve as the basis for the current study.
Gender differences in mathematics have received attention because studies show that male students outperform female students on higher-level cognitive tasks [ 31 ]. This is a shift from a meta-analysis study that found gender differences in mathematics to be insignificant and favored female students [ 32 ]. At the college level, female students slightly outperform male students in computation while male students outperform female students in problem solving. However, no gender differences have been observed among elementary and middle school students. This result was strengthened by other meta-analysis studies [ 7 , 8 ], which concluded that there was no gender difference in mathematical performance and problem-solving skills [ 15 , [33] , [35] , [34] ]. Gender similarity in mathematics is achieved when equal learning opportunities and educational choices are provided and the curriculum is expanded to include the needs and interests of the students [ 16 , 18 , 31 ].
From a sociological perspective, gender similarity in mathematics makes sense. If there is a gender difference in mathematics, this has been attributed to science, technology, engineering, and mathematics (STEM) being stereotyped as a male domain [ 8 ]. Stereotypes influence beliefs and self-efficacy of students and perceptions of their own abilities [ 8 , 19 ]. This is the reason for the low interest of female students in advanced mathematics courses [ 18 , 19 ]. However, Halpern et al. [ 16 ] found that more female students are entering many occupations that require a high level of mathematical knowledge. Moreover, Anjum [ 36 ] found that female students outperformed male students in mathematics. This may be because female students prepared better than the male students before the test and were more thorough [ 36 , 37 ]. The study of Anjum [ 36 ] is one of the basis cases of the current study.
Differences in brain structure support the argument that there are gender differences in mathematical performance [ 16 , 17 ]. Females have less brain lateralization (i.e., symmetric left and right hemispheres), which helps them perform better verbally. Meanwhile, males have more brain lateralization, which is important for spatial tasks [ 17 ]. In addition, the male hormone testosterone slows the development of the left hemisphere [ 16 ], which improves the performance of right brain-dominant mathematical reasoning and spatial tasks.
3.1. Instrumentation
In this study, a science-related mathematical problem-solving test was used. This is a mathematics essay test where the problems are in the form of scenarios related to environmental management. Problems are solved by using technology as a tool (e.g., calculator, grid paper). The test was developed in an interdisciplinary STEM framework, and it is targeted toward grades 7–9. There were six scenarios in total: some were given to multiple grades, and others were specific to a grade. They included ecofriendly packaging (grade 7), school park (grade 7), calorie vs. greenhouse gas emissions (grades 7–9), floodwater reservoir (grade 8), city park (grades 8–9), and infiltration well (grade 9). These scenarios cover topics such as number and measurement, ratio and proportion, geometry, and statistics. Every scenario had a challenge, and students were provided with eight metacognitive prompt items to help them explore their problem-solving skills.
The test was administered by using paper and pencils for a 3-h period with a break every hour. At the end of the test, students were asked to fill in their demographic information. Each prompt item had a maximum score of 5 points: a complete and correct answer (5 points), a complete answer with a minor error (4 points), an incomplete answer with a minor error (3 points), an incomplete answer with a major error (2 points), and a completely wrong and irrelevant answer (1 point). Each scenario had a maximum total score of 40 points.
The test was validated to determine whether it contained good and acceptable psychometric evidence. It had an acceptable content validity index (CVI >0.67), moderate intraclass correlation coefficient (ICC) (rxx = 0.63), and acceptable Cronbach's alpha (α = 0.84). The construct validity indicated all scenarios and prompt items were fit (0.77 ≤ weighted mean square ≤1.59) with an acceptable discrimination value (0.48 ≤ discrimination value ≤ 0.93), acceptable behavior of the rating score, and good reliability (scenario reliability = 0.86; prompt item reliability = 0.94).
3.2. Participants
The test was administered to grades 7–9 students in east Java, Indonesia (n = 1067). The students were selected from A-accreditation schools in urban and rural areas; random classes were selected for each grade. The majority of the students were Javanese (95.01%), with the remainder being Madurese (3.3%) and other ethnicities. Table 1 describes the demographics of the participants.
Demographic characteristics of participants.
| Demographic Characteristics | N | % | |
|---|---|---|---|
| Gender | Male | 452 | 42.4 |
| Female | 615 | 57.6 | |
| Grade | 7 (M age = 12.59, SD = 0.61) | 380 | 35.61 |
| 8 (M age = 13.42, SD = 0.59) | 331 | 31.02 | |
| 9 (M age = 14.50, SD = 0.59) | 356 | 33.36 | |
| School location | Rural | 427 | 40.02 |
| Urban | 640 | 59.89 | |
3.3. Data analysis
Data were collected between July and September 2022. Prior to data collection, ethical approval was sought from the institutional review board (IRB) of the Doctoral School of Education, University of Szeged and was granted with the ethical approval number of 7/2022. In addition, permission letters were sent to several schools to request permission and confirm their participation. The test answers of the students were scored by two raters – the first author of this study and a rater with master's degree in mathematics education – to ensure that the rating scale was consistently implemented. The results showed good consistency with an ICC of 0.992 and Cronbach's alpha of 0.996.
The scores from one of the raters were converted to a logit scale by weighted likelihood estimation (WLE) using the ConQuest software. A logit scale provides a consistent value or meaning in the form of intervals. The logit scale represents the unit interval between locations on the person–item map. WLE was chosen rather than maximum likelihood estimation (MLE) because WLE is more central than MLE, which helps to correct for bias [ 38 ]. The WLE scale was represented by using descriptive statistics to profile the students' mathematical problem-solving skills in terms of the percentage, mean score ( M ) and standard deviation ( SD ) for each phase. The WLE scale was also used to describe common difficulties for each phase. The development of students’ mathematical problem-solving skills across grades was presented by a pirate plot, which is used in R to visualize the relationship between 1 and 3 categorical independent variables and 1 continuous dependent variable. It was chosen because it displays raw data, descriptive statistics, and inferential statistics at the same time. The data analysis was performed using R studio version 4.1.3 software with the YaRrr package. A one-way ANOVA was performed to find significant differences across grades. An independent sample t -test was used to analyze significant differences based on gender and school location. The descriptive statistics, one-way ANOVA test, and independent sample t -test were performed using the IBM SPSS Statistics 25 software.
4.1. Student profiles
The scores of students were converted to the WLE scale, where a score of zero represented a student with average ability, a positive score indicated above-average ability, and a negative score indicated below-average ability. A higher score indicated higher ability. The mean score represented a student with average mathematical problem-solving skills ( M = 0.001, SD = 0.39). Overall, 52.1% of students had a score below zero. The distribution of scores among students was predominantly in the interval between −1 and 0. When the problem-solving process was analyzed by phase, the results showed that exploring and understanding were the most mastered problem-solving skills ( M = 0.24, SD = 0.51). Only 27.9% of students had below-average scores for the exploring and understanding phases, which indicates that they mostly understood the given problem and recognized the important information. However, the problem-solving skills decreased with higher phases. The students had below-average abilities in the phases of representing and formulating ( M = −0.01, SD = 0.36), planning and executing ( M = −0.15, SD = 0.41), and monitoring and reflecting ( M = −0.16, SD = 0.36). About 57.9% of the students had below-average scores for the representing and formulating phase, which indicates that they had problems making hypotheses regarding science phenomena, representing problems in mathematical form, and designing a prototype. The obvious reason for their difficulty with making hypotheses was that they did not understand simple concepts of science (e.g., CO 2 vs. O 2 ). In the planning and executing phase, 66.8% of the students failed to achieve a score greater than zero. This happened because they failed to apply mathematical concepts and procedures. Because they were unable to plan and execute a strategy, this affected the next phase of the problem-solving process. In the monitoring and reflecting phase, 68.0% of the students had a below-average score.
4.2. Development of mathematical problem-solving skills across grades
The development of the mathematical problem-solving skills of the students across grades was observed based on the increase in the mean score. The problem-solving skills developed from grade 7 to grade 8. The students of grade 7 had a mean score of −0.04 while grade 8 students had the highest mean score of 0.03. The students in grades 7 and 8 also showed more varied problem-solving skills than the grade 9 students did. In contrast, the grade 9 students showed a different pattern of development, and their mean score dropped to 0.01. Although the difference was not large, further analysis was needed to determine its significance.
Fig. 1 displays the development of the mathematical problem-solving skills of the students. The dots represent raw data or WLE scores. The middle line shows the mean score. The beans represent a smoothed density curve showing the full data distribution. The scores of the students in grades 7 and 9 were concentrated in the interval between −0.5 and 0. However, the scores of the grade 8 students were concentrated in the interval between 0 and 0.5. The scores of the students in grades 7 and 8 showed a wider distribution than those of the grade 9 students. The bands which overlap with the line representing the mean score, define the inference around the mean (i.e., 95% of the data are in this interval). The inference of the WLE score was close to the mean.

Differences in students' mathematical problem-solving skills across grades.
Note : PS: Problem-Solving Skills of Students.
The one-way ANOVA results indicated a significant difference among the problem-solving skills of the students of grades 7–9 ( F (1,066) = 3.01, p = 0.046). The students of grade 8 showed a significant difference in problem-solving skills and outperformed the other students. The students of grades 7 and 9 showed no significant difference in their mathematical problem-solving skills. Table 2 presents the one-way ANOVA results of the mathematical problem-solving skills across grades.
One-way ANOVA results of the mathematical problem-solving across grades.
| Grades | N | (1,066) | Significant difference between the sub-samples | |||
|---|---|---|---|---|---|---|
| 7 | 380 | −0.04 | 0.42 | 3.01 | .046 | {7, 9} < {8} |
| 8 | 331 | 0.03 | 0.44 | |||
| 9 | 356 | 0.01 | 0.29 |
Note. Post hoc test: Dunnett's T3. 7, 8, and 9: subsample grade. <: direction of significant difference ( p < 0.05).
Fig. 2 shows the development of the mathematical problem-solving skills of the students across grades based on school location and gender. The problem-solving skills of the urban students increased from a mean score of 0.07 in grade 7 to 0.14 in grade 8. However, the mean score of urban students in grade 9 dropped. In contrast, the mean scores of the rural students increased continuously with grade. The improvements were significant for both the rural ( F (426) = 10.10, p < 0.001) and urban ( F (639) = 6.10, p < 0.01) students. For the rural students, grade 9 students showed a significant difference in problem-solving skills. In contrast, urban students in grades 8 and 9 showed significant differences in problem-solving skills but not in grade 7.

Differences in students' mathematical problem-solving skills across grades and different demographic backgrounds.
(a) Differences in students grade 7 of mathematical problem-solving skills across grades and different demographic backgrounds
(b) Differences in students grade 8 of mathematical problem-solving skills across grades and different demographic backgrounds
(c) Differences in students grade 9 of mathematical problem-solving skills across grades and different demographic backgrounds
Note: WLE_PS: The students' problem-solving skills in WLE scale; F: Female; M: Male; ScLoc: School location; R: Rural; U: Urban.
When divided by gender, both female and male students showed improvements in their problem-solving skills from grades 7 and 8. However, female students in grade 9 showed a stable score while the scores of male students in grade 9 declined. Only male students in grade 7 showed a significant difference in the mean score. In urban schools, the scores of male and female students increased and decreased, respectively, from grade 7 to grade 8. Male students in rural schools showed an increase in score from grade 7 to grade 9. However, the scores of female students in rural schools decreased from grade 7 to grade 8. Table 3 presents the one-way ANOVA results for the mathematical problem-solving skills of the students considering gender and school location.
One-way ANOVA results for mathematical problem-solving skills across grades and different demographic backgrounds.
| Grade | Significant difference between the sub-samples | ||||||
|---|---|---|---|---|---|---|---|
| Rural | 7 | 168 | −0.18 | 0.34 | < | {7, 8} < {9} | |
| 8 | 155 | −0.10 | 0.46 | ||||
| 9 | 104 | 0.03 | 0.25 | ||||
| Urban | 7 | 212 | 0.07 | 0.44 | F(639) = 6.10 | .001 | {7, 9} < {8} |
| 8 | 176 | 0.14 | 0.38 | ||||
| 9 | 252 | 0.05 | 0.30 | ||||
| Female | 7 | 219 | 0.03 | 0.44 | F(614) = 0.18 | .84 | – |
| 8 | 204 | 0.05 | 0.45 | ||||
| 9 | 192 | 0.05 | 0.26 | ||||
| Male | 7 | 161 | −0.13 | 0.36 | F(451) = 5.28 | .005 | {7} < {8, 9} |
| 8 | 127 | 0.001 | 0.42 | ||||
| 9 | 164 | −0.03 | 0.32 |
Fig. 2 shows that the distributions of the male and female scores of students were similar for every grade except rural grade 9 students. The scores of the rural female students were concentrated in the interval between 0 and 0.5 while the scores of the rural male students were mostly below 0. The scores of rural students in grade 7 and urban students in grade 9 (both male and female) were concentrated in the interval between −0.5 and 0. The scores of urban students in grades 7 and 8 were concentrated in the interval between −0.5 and 0.5.
Fig. 3 shows a detailed analysis of the development of mathematical problem-solving skills across grades for each phase of the problem-solving process. Similar patterns were observed in the exploring and understanding and the representing and formulating phases: the mean score increased from grade 7 to grade 8 but decreased from grade 8 to grade 9. Grade 8 students had the highest mean score and differed significantly from the scores of students in other grades.

Differences in students' mathematical problem-solving skills in every phase across grades: (1) Exploring & understanding, (2) Representing & formulating, (3) Planning & executing, (4) Monitoring & reflecting.
(a) Differences in students' mathematical problem-solving skills in exploring and understanding phase
(b) Differences in students' mathematical problem-solving skills in representing and formulating phase
(c) Differences in students' mathematical problem-solving skills in planning and executing phase
(d) Differences in students' mathematical problem-solving skills in monitoring and reflecting phase
Note: WLE_Exp_Un: The WLE score in exploring and understanding; WLE_Rep_For: The WLE score in representing and formulating; WLE_Plan_Ex: The WLE score in planning and executing; WLE_Mon_Ref: The WLE score in monitoring and reflecting.
The scores of the students for the planning and executing phase increased with grade. However, the difference was only significant at grade 9. Grades 7 and 8 students showed an increase in score, but the improvement was not significant. There was no pattern detected in the monitoring and reflecting phase. The score was stable for grades 7 and 8 students but improved for grade 9 students. The mean score for each phase and the one-way ANOVA results are presented in Table 4 .
One-way ANOVA results for every phase of problem-solving across grades.
| Phases | Grade | (1,066) | ||||
|---|---|---|---|---|---|---|
| Exploring & Understanding | 7 | 0.19 | 0.54 | 3.98 | .019 | {7, 9} < {8} |
| 8 | 0.30 | 0.54 | ||||
| 9 | 0.25 | 0.44 | ||||
| Representing & Formulating | 7 | −0.03 | 0.37 | 16.20 | <.001 | {7, 9} < {8} |
| 8 | 0.07 | 0.42 | ||||
| 9 | −0.08 | 0.26 | ||||
| Planning & Executing | 7 | −0.18 | 0.42 | 3.20 | .041 | {9} < {7, 8} |
| 8 | −0.17 | 0.51 | ||||
| 9 | −0.11 | 0.24 | ||||
| Monitoring & Reflecting | 7 | −0.17 | 0.41 | 1.48 | .228 | – |
| 8 | −0.17 | 0.41 | ||||
| 9 | −0.13 | 0.23 |
Fig. 3 shows that the distributions of the problem-solving skills of the students were similar across grades and phases. However, the distributions were different for grade 9 students in the representing and formulating, planning and executing, and monitoring and reflecting phases, where 95% of the data were in the interval between −0.5 and 0.5.
4.3. Effects of demographic background
4.3.1. school location.
The mathematical problem-solving skills of the students differed significantly based on school location. Urban students scored higher than rural students. The results of the t -test for mathematical problem-solving skills based on school location are presented in Table 5 .
T-test results for mathematical problem-solving skills based on school location.
| Location | (1065) | ||||||
|---|---|---|---|---|---|---|---|
| Rural | 427 | −0.10 | 0.38 | 0.18 | .674 | −6.90 | <.001 |
| Urban | 640 | 0.07 | 0.38 |
The effects of the school's location on the performances of male and female students were analyzed. The results showed that the scores of the female students differed significantly based on school location ( t (613) = −6.09, p < 0.001). Female students in urban schools ( M = 0.18, SD = 0.39) outperformed female students in rural schools ( M = −0.08, SD = 0.37). Similar results were observed for male students with urban students ( M = −0.01, SD = 0.35) outperforming rural students ( M = −0.12, SD = 0.39) by a significant margin ( t (382.764) = −3.25, p < 0.01).
When analyzed by grade, grades 7 and 8 students contributed to the difference based on school location with t (377.952) = −6.34, p < 0.001 and t (300.070) = −5.04, p < 0.001, respectively. Urban students in grades 7 and 8 performed significantly better than their rural counterparts did. However, there was no significant difference between rural and urban students in grade 9 ( t (354) = 0.71, p = 0.447).
4.3.2. Gender
Male and female students showed a significant difference in their mathematical problem-solving skills. Overall, female students outperformed male students. The detailed results of the independent sample t -test for mathematical problem-solving skills based on gender are presented in Table 6 .
T-test results for mathematical problem-solving skills based on gender.
| Gender | (1006,013) | ||||||
|---|---|---|---|---|---|---|---|
| Female | 615 | 0.04 | 0.39 | 5.20 | .023 | −4.312 | <.001 |
| Male | 452 | −0.06 | 0.38 |
The results were analyzed to determine whether the school location contributed to the gender difference. The gender difference was most significant among urban students ( t (596.796) = −4.36, p < 0.001). Female students from urban schools ( M = 0.12, SD = 0.39) outperformed male students from urban schools ( M = −0.01, SD = 0.35). There was no significant difference between female and male students from rural schools ( t (425) = −1.31, p = 0.191).
Grades 7 and 9 students contributed to the gender difference with t (372.996) = −3.90, p < 0.001 and t (354) = −2.73, p < 0.01, respectively. Female students in grades 7 and 9 outperformed their male counterparts. However, there was no significant gender difference among grade 8 students ( t (329) = −0.10, p = 0.323).
5. Discussion
The mathematical problem-solving skills of the students were categorized as average. In addition, the difficulties of students increased in line with the problem-solving phase. Fewer students failed the exploring and understanding phase than the subsequent phases. This confirms the results of previous studies indicating that more students failed further along the problem-solving process [ 25 , 26 ]. Because the problem-solving process is sequential, students who have difficulty understanding a problem will fail the subsequent phases [ 27 ].
The development of mathematical problem-solving skills was evaluated according to the mean WLE score. The mathematical problem-solving skills of the students developed from grade 7 to grade 8 based on the increase in their mean scores. However, the development dropped in grade 9. This agrees with previous results that concluded that higher grades had the highest problem-solving skills, but the fastest skill development took place in grades 7–8 after which it dropped [ 3 , 4 ]. These results indicate that the mathematical problem-solving skills of the students should improve and be strengthened in grades 7–8, which will help them perform better in grade 9.
In this study, the effects of the demographic background of the students were analyzed in detail, which is an aspect missing from previous studies. The results showed that the mathematical problem-solving skills of urban students increased from grade 7 to grade 8 but decreased in grade 9. The same pattern was found among male and female students. However, a different pattern was observed for rural students, where the skills of grade 9 students continued to increase. The different patterns may be attributed to a structural reorganization of cognitive processes at a particular age [ 3 ]. However, more research is needed on the effects of the demographic backgrounds of students on mathematical problem-solving skills. These results were different from previous results because the previous studies only analyzed the development in general, without focusing on their demographic background. Hence, different patterns of development were observed when it was thoroughly examined.
Because solving problems is a cognitive process, the development of problem-solving skills for particular phases and processes needed to be analyzed. The students showed the same pattern for knowledge acquisition (i.e., exploring and understanding, and representing and formulating phases), with an increase in skill from grade 7 to grade 8 but a decrease in grade 9. However, the students showed increasing skill in knowledge application (i.e., planning and executing, as well as monitoring and reflecting phases) across grades. This means that the difference between the mean scores in grade 9 was not significant across phases. Grade 9 students had lower scores than grade 8 students for the knowledge acquisition phase but higher scores for the knowledge application phase. In contrast, the gap between the mean scores of grades 7 and 8 was large across phases.
These results proved that there is a significant difference in the mathematical problem-solving skills of students based on their demographic backgrounds. The urban students outperformed rural students, which confirms the results of previous studies [ 9 , 10 , 15 ]. The difference can be attributed to the availability of facilities, teacher quality, and interactive teaching and learning instruction [ 6 ]. In Indonesia, the policies for the public educational system for middle schools are set at the municipal level. This means that each city has its own policies for teacher training, teacher recruitment, teaching and learning processes, facilities, etc. Urban schools mostly have stricter policies as well as various programs to help students improve their knowledge and skills. In addition, they have supportive facilities for teaching and learning. This unequal environment is the strongest reason for the difference in mathematical problem-solving skills.
The results were analyzed in detail to observe which groups in the rural and urban schools contributed to the difference. Both male and female students in urban schools performed better than their counterparts in rural schools did. In addition, urban students in grades 7 and 8 outperformed their rural counterparts. There was no significant difference between urban and rural students in grade 9. This may be because grade 9 is the last grade in middle school, so students have to prepare for high school entrance requirements, including exam and/or grade point average scores. Hence, both rural and urban schools focus much effort on the teaching and learning process in this grade.
In this study, the female students surprisingly had better mathematical problem-solving skills than the male students did. This confirmed the results of the meta-analysis by Hyde et al. [ 32 ] and study by Anjum [ 36 ], which found that female students slightly outperformed male students in mathematics. This difference may be because of motivation and attitude [ 39 , 40 ]. Female Indonesian students are typically more diligent, thorough, responsible, persistent, and serious with their tasks.
A detailed analysis was performed to evaluate which group of students contributed to the gender differences. The results showed that female students outperformed male students in urban schools. This may be because male students at urban schools typically display an unserious attitude toward low-stake tests. In addition, female students outperformed their male counterparts in grades 7 and 9. The reason for this difference requires further analysis.
6. Conclusion
Studying the problem-solving skills of students is crucial to facilitating their development. In this study, the conclusions are presented as follows:
- • The mathematical problem-solving skills of the students were categorized as average. More students failed at higher phases of the problem-solving process.
- • Students showed development of their mathematical problem-solving skills from grade 7 to grade 8 but a decline in grade 9. The same pattern was detected across grades for urban students, both female and male. However, the problem-solving skills of rural students increased with the grade.
- • A similar development was observed for the individual problem-solving phases. In the knowledge acquisition phase, the problem-solving skills of the students developed from grade 7 to grade 8 but decreased in grade 9. However, problem-solving skills increased across grades in the knowledge application phase.
- • The school location was shown to have a significant effect on the mathematical problem-solving skills of the students. Urban students generally outperform students in rural schools. However, gender and grade contributed to differences in mathematical problem-solving skills based on school location. Female and male urban students in grades 7 and 8 outperformed their rural counterparts.
- • In general, female students outperformed male students in mathematical problem-solving skills, particularly those from urban schools and in grades 7 and 9.
The sampling method and the number of demographic backgrounds limited the scope of this study. Only students from A-accreditation schools were selected because higher-order problem-solving skills were considered assets. Moreover, the study only included three demographic factors: grade, gender, and school location. More demographic information, such as school type, can be added (public or private schools). Hence, future studies will need to broaden the sample size and consider more demographic factors. Despite these limitations, this study can help teachers determine the best period for enhancing the development of mathematical problem-solving skills. Moreover, the differences in mathematical problem-solving skills due to demographic background can be used as a basis for educational policymakers and teachers to provide equal opportunity and equitable education to students.
Author contribution statement
Ijtihadi Kamilia Amalina: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Tibor Vidákovich: Conceived and designed the experiments; Contributed reagents, materials, analysis tools or data.
Funding statement
This work was supported by University of Szeged Open Access Fund with the grant number of 6020.
Data availability statement
Additional information.
No additional information is available for this paper.
Declaration of competing interest
No potential conflict of interest was reported by the authors.

Problem Solving Skills: 25 Performance Review Phrases Examples
By Status.net Editorial Team on July 21, 2023 — 4 minutes to read
Problem solving is an important skill in any work environment: it includes the ability to identify, understand, and develop solutions to complex issues while maintaining a focus on the end goal. Evaluating this skill in employees during performance reviews can be highly beneficial for both the employee and the organization.
Questions that can help you determine an employee’s rating for problem solving skills:
- How well does the employee define the problem and identify its root cause?
- How creative is the employee in generating potential solutions?
- How effective is the employee in implementing the chosen solution?
- How well does the employee evaluate the effectiveness of the solution and adjust it if necessary?
Related: Best Performance Review Examples for 48 Key Skills
2000+ Performance Review Phrases: The Complete List (Performance Feedback Examples)
Performance Review Phrases and Paragraphs Examples For Problem Solving
5 – outstanding.
Phrases examples:
- Consistently demonstrates exceptional problem-solving abilities
- Proactively identifies issues and offers innovative solutions
- Quickly adapts to unforeseen challenges and finds effective resolutions
- Exceptional problem-solving ability, consistently providing innovative solutions
- Regularly goes above and beyond to find creative solutions to complicated issues
- Demonstrates a keen understanding of complex problems and quickly identifies effective solutions
Paragraph Example 1
“Jane consistently demonstrates outstanding problem-solving skills. She proactively identifies issues in our department and offers innovative solutions that have improved processes and productivity. Her ability to quickly adapt to unforeseen challenges and find effective resolutions is commendable and has proven invaluable to the team.”
Paragraph Example 2
“Sarah has demonstrated an outstanding ability in problem solving throughout the year. Her innovative solutions have significantly improved our department’s efficiency, and she consistently goes above and beyond expectations to find creative approaches to complicated issues.”
4 – Exceeds Expectations
- Demonstrates a strong aptitude for solving complex problems
- Often takes initiative in identifying and resolving issues
- Effectively considers multiple perspectives and approaches before making decisions
- Displayed a consistently strong ability to tackle challenging problems efficiently
- Often takes the initiative to solve problems before they escalate
- Demonstrates a high level of critical thinking when resolving issues
“John exceeds expectations in problem-solving. He has a strong aptitude for solving complex problems and often takes initiative in identifying and resolving issues. His ability to consider multiple perspectives and approaches before making decisions has led to valuable improvements within the team.”
“Sam consistently exceeded expectations in problem solving this year. His efficient handling of challenging issues has made a positive impact on our team, and he often takes the initiative to resolve problems before they escalate. Sam’s critical thinking ability has been a valuable asset to our organization, and we appreciate his efforts.”
3 – Meets Expectations
- Displays adequate problem-solving skills when faced with challenges
- Generally able to identify issues and propose viable solutions
- Seeks assistance when necessary to resolve difficult situations
- Demonstrates a solid understanding of problem-solving techniques
- Capable of resolving everyday issues independently
- Shows perseverance when facing difficult challenges
“Mary meets expectations in her problem-solving abilities. She displays adequate skills when faced with challenges and is generally able to identify issues and propose viable solutions. Mary also seeks assistance when necessary to resolve difficult situations, demonstrating her willingness to collaborate and learn.”
“Sarah meets expectations in her problem-solving abilities. She demonstrates a solid understanding of problem-solving techniques and can resolve everyday issues independently. We value her perseverance when facing difficult challenges and encourage her to continue developing these skills.”
2 – Needs Improvement
- Struggles to find effective solutions to problems
- Tends to overlook critical details when evaluating situations
- Reluctant to seek help or collaborate with others to resolve issues
- Struggles to find effective solutions when faced with complex issues
- Often relies on assistance from others to resolve problems
- May lack confidence in decision-making when solving problems
“Tom’s problem-solving skills need improvement. He struggles to find effective solutions to problems and tends to overlook critical details when evaluating situations. Tom should work on being more willing to seek help and collaborate with others to resolve issues, which will ultimately strengthen his problem-solving abilities.”
“Mark’s problem-solving skills need improvement. He often struggles to find effective solutions for complex issues and seeks assistance from others to resolve problems. We encourage Mark to build his confidence in decision-making and focus on developing his problem-solving abilities.”
1 – Unacceptable
- Fails to identify and resolve problems in a timely manner
- Lacks critical thinking skills necessary for effective problem-solving
- Often creates additional issues when attempting to resolve problems
- Demonstrates a consistent inability to resolve even basic issues
- Often avoids responsibility for problem-solving tasks
- Fails to analyze problems effectively, leading to poor decision-making
“Sally’s problem-solving skills are unacceptable. She consistently fails to identify and resolve problems in a timely manner, and her lack of critical thinking skills hinders her ability to effectively solve challenges. Additionally, her attempts to resolve problems often create additional issues, resulting in a negative impact on the team’s overall performance.”
“Susan’s problem-solving performance has been unacceptable this year. She consistently demonstrates an inability to resolve basic issues and avoids taking responsibility for problem-solving tasks. Her ineffectiveness in analyzing problems has led to poor decision-making. It is crucial that Susan improve her problem-solving skills to succeed in her role.”
- Job Knowledge Performance Review Phrases (Examples)
- Cooperation Skills: 25 Performance Review Phrases Examples
- 100 Performance Review Phrases for Job Knowledge, Judgment, Listening Skills
- 10 Examples: What Are Analytical Skills?
- Collaboration Skills: 25 Performance Review Phrases Examples
- Critical Thinking: 25 Performance Review Phrases Examples
Measuring cognitive load with subjective rating scales during problem solving: differences between immediate and delayed ratings
- Published: 21 August 2014
- Volume 43 , pages 93–114, ( 2015 )

Cite this article

- Annett Schmeck 1 ,
- Maria Opfermann 1 ,
- Tamara van Gog 2 ,
- Fred Paas 2 &
- Detlev Leutner 1
5080 Accesses
114 Citations
1 Altmetric
Explore all metrics
Subjective cognitive load (CL) rating scales are widely used in educational research. However, there are still some open questions regarding the point of time at which such scales should be applied. Whereas some studies apply rating scales directly after each step or task and use an average of these ratings, others assess CL only once after the whole learning or problem-solving phase. To investigate if these two approaches are comparable indicators of experienced CL, two experiments were conducted, in which 168 and 107 teacher education university students, respectively, worked through a sequence of six problems. CL was assessed by means of subjective ratings of mental effort and perceived task difficulty after each problem and after the whole process. Results showed that the delayed ratings of both effort and difficulty were significantly higher than the average of the six ratings made during problem solving. In addition, the problems we assumed to be of higher complexity seemed to be the best predictors for the delayed ratings. Interestingly, for ratings of affective variables, such as interest and motivation, the delayed rating did not differ from the average of immediate ratings.
This is a preview of subscription content, log in via an institution to check access.
Access this article
Price includes VAT (Russian Federation)
Instant access to the full article PDF.
Rent this article via DeepDyve
Institutional subscriptions
Similar content being viewed by others

Stage Theory of Cognitive Development—Jean Piaget

A Historical Review of Collaborative Learning and Cooperative Learning
Theory of human motivation—abraham maslow.
Antonenko, P., & Niederhauser, D. (2010). The influence of leads on cognitive load and learning in a hypertext-assisted learning environment. Computers in Human Behavior, 26 , 140–150.
Article Google Scholar
Antonenko, P., Paas, F., Grabner, R., & Van Gog, T. (2010). Using electroencephalography (EEG) to measure cognitive load. Educational Psychology Review, 22 , 425–438.
Ayres, P. (2006). Using subjective measures to detect variations of intrinsic load within problems. Learning and Instruction, 16 , 389–400.
Bratfisch, O., Borg, G., & Dornic, S. (1972). Perceived item difficulty in three tests of intellectual performance capacity . Stockholm: Institute of Applied Psychology, Report No. 29.
Brünken, R., Plass, J. L., & Leutner, D. (2003). Direct measurement of cognitive load in multimedia learning. Educational Psychologist, 38 , 53–61.
Brünken, R., Plass, J. L., & Leutner, D. (2004). Assessment of cognitive load in multimedia learning with dual-task methodology: Auditory load and modality effects. Instructional Science, 32 , 115–132.
Chandler, P., & Sweller, J. (1991). Cognitive load theory and the format of instruction. Cognition and Instruction, 8 , 293–332.
Chandler, P., & Sweller, J. (1992). The split-attention effect as a factor in the design of instruction. British Journal of Educational Psychology, 62 , 233–246.
Chandler, P., & Sweller, J. (1996). Cognitive load while learning to use a computer program. Applied Cognitive Psychology, 10 , 1–20.
de Jong, T. (2010). Cognitive load theory, educational research, and instructional design: Some food for thought. Instructional Science, 38 , 105–134.
Kalyuga, S., Chandler, P., & Sweller, J. (1999). Managing split-attention and redundancy in multimedia instruction. Applied Cognitive Psychology, 13 , 351–371.
Kalyuga, S., Chandler, P., Tuovinen, J., & Sweller, J. (2001). When problem solving is superior to studying worked examples. Journal of Educational Psychology, 93 , 579–588.
Kühl, T., Scheiter, K., Gerjets, P., & Edelmann, J. (2011). The influence of text modality on learning with static and dynamic visualizations. Computers in Human Behavior, 27 , 29–35.
Kuusela, H., & Paul, P. (2000). A comparison of concurrent and retrospective verbal protocol analysis. American Journal of Psychology, 113 , 387–404.
Leutner, D., Leopold, C., & Sumfleth, E. (2009). Cognitive load and science text comprehension: Effects of drawing and mentally imagining text content. Computers in Human Behavior, 25 , 284–289.
Logie, R. H. (1995). Visuo-spatial working memory . Hove, UK: Lawrence Erlbaum Associates.
Google Scholar
Marcus, N., Cooper, M., & Sweller, J. (1996). Understanding instructions. Journal of Educational Psychology, 88 , 49–63.
Opfermann, M. (2008). There’s more to it than instructional design: The role of individual learner characteristics for hypermedia learning . Berlin, Germany: Logos.
Paas, F. (1992). Training strategies for attaining transfer of problem-solving skill in statistics: A cognitive-load approach. Journal of Educational Psychology, 84 , 429–434.
Paas, F., Ayres, P., & Pachman, M. (2008). Assessment of cognitive load in multimedia learning: Theory, methods and applications. In D. Robinson & G. Schraw (Eds.), Recent innovations in educational technology that facilitate student learning (pp. 20–36). Charlotte, NC: Information Age Publishing.
Paas, F., Renkl, A., & Sweller, J. (2003a). Cognitive load theory and instructional design: Recent developments. Educational Psychologist, 38 , 1–4.
Paas, F., Tuovinen, J., Tabbers, H. K., & Van Gerven, P. W. M. (2003b). Cognitive load measurement as a means to advance cognitive load theory. Educational Psychologist, 38 , 63–71.
Paas, F., & van Merriënboer, J. J. G. (1994). Variability of worked examples and transfer of geometrical problem solving skills: A cognitive-load approach. Journal of Educational Psychology, 86 , 122–133.
Paas, F., van Merriënboer, J. J. G., & Adam, J. J. (1994). Measurement of cognitive load in instructional research. Perceptual and Motor Skills, 79 , 419–430.
Park, B., Moreno, R., Seufert, T., & Brünken, R. (2011). Does cognitive load moderate the seductive details effect? A multimedia study. Computers in Human Behavior, 27 , 5–10.
Plass, J. L., Moreno, R., & Brünken, R. (Eds.). (2010). Cognitive load: Theory & application . Cambridge: Cambridge University Press.
Renkl, A., Gruber, H., Weber, S., Lerche, T., & Schweizer, K. (2003). Cognitive Load beim Lernen aus Lösungsbeispielen [Cognitive load of learning from worked-out examples]. Zeitschrift für Pädagogische Psychologie, 17 , 93–101.
Rheinberg, F., Vollmeyer, R., & Burns, B. D. (2001). FAM: Ein Fragebogen zur Erfassung aktueller Motivation in Lern- und Leistungssituationen [QCM: A questionnaire to assess current motivation in learning situations]. Diagnostica, 47 , 57–66.
Schwamborn, A., Thillmann, H., Opfermann, M., & Leutner, D. (2011). Cognitive load and instructionally supported learning with provided and learner-generated visualizations. Computer in Human Behavior, 27 , 89–93.
Seufert, T., & Brünken, R. (2006). Cognitive load and the format of instructional aids for coherence formation. Applied Cognitive Psychology, 20 , 321–331.
Sweller, J. (1988). Cognitive load during problem solving: Effects on learning. Cognitive Science, 12 , 257–285.
Sweller, J. (1993). Some cognitive processes and their consequences for the organization and presentation of information. Australian Journal of Psychology, 45 , 1–8.
Sweller, J. (2010). Element interactivity and intrinsic, extraneous and germane cognitive load. Educational Psychology Review, 22 , 123–138.
Sweller, J., Ayres, P., & Kalyuga, S. (2011). Cognitive load theory . New York: Springer.
Book Google Scholar
Sweller, J., van Merriënboer, J. J. G., & Paas, F. (1998). Cognitive architecture and instructional design. Educational Psychology Review, 10 , 251–296.
Tabbers, H. K., Martens, R. L., & van Merriënboer, J. J. G. (2004). Multimedia instructions and cognitive load theory: Effects of modality and cueing. British Journal of Educational Psychology, 74 , 71–81.
Taylor, K. L., & Dionne, J.-P. (2000). Accessing problem-solving strategy knowledge: The complementary use of concurrent verbal protocols and retrospective debriefing. Journal of Educational Psychology, 92 , 413–425.
Van Gerven, P. W. M., Paas, F., van Merriënboer, J. J. G., & Schmidt, H. G. (2004). Memory load and the cognitive pupillary response in aging. Psychophysiology, 41 , 167–174.
Van Gog, T., & Jarodzka, H. (2013). Eye tracking as a tool to study and enhance cognitive and metacognitive processes in computer-based learning environments. In R. Azevedo & V. Aleven (Eds.), International handbook of metacognition and learning technologies (pp. 143–156). New York: Springer.
Van Gog, T., Kirschner, F., Kester, L., & Paas, F. (2012). Timing and frequency of mental effort measurement: Evidence in favor of repeated measures. Applied Cognitive Psychology, 26 , 833–839.
Van Gog, T., & Paas, F. (2008). Instructional efficiency: Revisiting the original construct in educational research. Educational Psychologist, 43 , 16–26.
Van Gog, T., Paas, F., & van Merriënboer, J. J. G. (2006). Effects of process-oriented worked examples on troubleshooting transfer performance. Learning and Instruction, 16 , 154–164.
Van Merriënboer, J. J. G., & Sweller, J. (2005). Cognitive load theory and complex learning: Recent developments and future directions. Educational Psychology Review, 17 , 147–177.
Download references
Author information
Authors and affiliations.
Department of Instructional Psychology, Faculty for Educational Sciences, University of Duisburg-Essen, 45117, Essen, Germany
Annett Schmeck, Maria Opfermann & Detlev Leutner
Capaciteitsgroep Psychologie, Faculteit der Sociale Wetenschappen, Erasmus University Rotterdam, Burgemeester Oudlaan 50, T-gebouw, P.O. Box 1738, 3000 DR, Rotterdam, The Netherlands
Tamara van Gog & Fred Paas
You can also search for this author in PubMed Google Scholar
Corresponding author
Correspondence to Annett Schmeck .
Weekday problems (according to order of presentation in Experiment 1)
Suppose today is Tuesday. What day of the week is the day after tomorrow?
Suppose today is Thursday. What day of the week is in three days?
Suppose yesterday was Wednesday. What day of the week was four days before the day before yesterday?
What day was yesterday if the day after the day after tomorrow is three days before Sunday?
Suppose five days after the day before yesterday is Friday. What day of the week is tomorrow?
Suppose last Tuesday was the 2nd day. What day of the week is it in 17 days, if the 8th day is in two days?
Rights and permissions
Reprints and permissions
About this article
Schmeck, A., Opfermann, M., van Gog, T. et al. Measuring cognitive load with subjective rating scales during problem solving: differences between immediate and delayed ratings. Instr Sci 43 , 93–114 (2015). https://doi.org/10.1007/s11251-014-9328-3
Download citation
Received : 28 November 2013
Accepted : 21 July 2014
Published : 21 August 2014
Issue Date : January 2015
DOI : https://doi.org/10.1007/s11251-014-9328-3
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Cognitive load
- Problem solving
- Mental effort
- Task difficulty
- Measurement
- Find a journal
- Publish with us
- Track your research
.png)
Quicklinks
10 performance rating scale examples scrutinized: scale up your reviews.

As you're looking to improve performance evaluation, it's always a good idea to brush up on the mechanics of performance rating scales.
With a myriad of rating scales out there, which one strikes the right chord? Which resonates with your organization's tempo and aligns with its goals? And, crucially, how do you ensure it's fair and balanced?
This article will:
- Look at different types of performance rating scales.
- Scrutinize 10 real-life examples you can readily implement or customize within your evaluation frameworks. (We include the scales, the definitions, the whole thing!)
- Share a checklist of factors to consider to define a rating scale that delivers transparent, substantial, and constructive feedback to enhance every employee's progress and development.

🔢 What is a performance rating scale ?
Performance rating scales are a standardized tool for assessing an employee's job performanc e based on predetermined criteria or expectations . These evaluations allow organizations to measure how effectively employees fulfill their job responsibilities and contribute to the company's objectives.

In turn, managers can quantify whether performance exceeds expectations regarding their effectiveness, contributions, and output. Additionally, a performance scale lets managers establish explicit performance targets and action plans. These goals provide employees with clear guidance for task completion and skill development, preparing them for employee appraisal .
Performance assessments typically use a rating scale or scoring system to evaluate various facets of an employee's performance, focusing on productivity, work quality, communication, teamwork, problem-solving, adaptability, and alignment with company values.

Why rating scales matter
Performance rating scales provide a standardized framework for evaluating employees . This ensures that all employees are assessed using the same criteria, leading to fairness and consistency in evaluations.
Rating scales are also designed to align with the organization's goals and objectives. They help communicate what's expected from employees regarding performance and behavior. This reduces ambiguity and ensures managers and employees have a shared understanding of performance expectations .
🕵️♀️ 6 Types of performance review rating scales

Five-point rating scale
A five-point scale is a commonly used rating system that provides five options for assessing or measuring a particular trait, characteristic, or performance level.
Each option on the scale represents a distinct level of the evaluated attribute.
Often, a five-point scale ranges from a low point to a high point, with a neutral or middle option in the center. The scale is typically represented numerically, with 1 as the lowest level and 5 as the highest.
One example of a 5-point scale is:
- unacceptable performance;
- partially successful;
- fully successful;
- distinguished performance.
A simpler 5-point scale is:
- unacceptable;
- needs improvement;
- acceptable;
- excellent.
Three-point rating scale
A three-point scale is a rating system that provides three distinct options for assessing or measuring a particular trait, characteristic, or performance level. Each option on the scale represents a different level of the evaluated attribute.
Like with the five-point rating scale, you can represent a three-point scale numerically or through descriptive labels. The options typically range from a low point to a high point, with one single neutral or middle option in between.
For example, Williams College's Competency-based form uses a 3-point scale with the following ratings:
- Exceeds expectations: Performance consistently exceeded expectations in all essential areas of responsibility, and the quality of work overall was excellent.
- Effective: Performance consistently met expectations in all essential areas of responsibility, at times possibly exceeding expectations, and the quality of work overall was very good.
- Improvement needed : Performance failed to meet expectations in one or more essential areas of responsibility. The employee needs to acquire and/or develop the necessary skills to build and sustain performance standards.

Four-point rating scale
A four-point scale for performance reviews is a rating system for assessing employee performance across various competencies or tasks. This scale consists of four levels, each representing a different degree of proficiency or achievement.
This type of scale is often preferred because it avoids a neutral or middle option (the 3-point and the 5-point scales have this), compelling the reviewer to make a more definitive judgment about the performance .
Duke University offers a performance rating example on a 4-point system:
Exceeds Expectations
- Performance clearly and consistently exceeds communicated performance requirements.
- Contributes to the organization's success well beyond job requirements. Contributes unique, innovative, and workable solutions to projects/problems.
Achievements and abilities are obvious to subordinates, peers, managers, and customers.
Fully Achieves Expectations
- Performance consistently meets the requirements, standards, or objectives of the job.
- Occasionally exceeds requirements. Results can be expected which are timely and accurate with minimum supervision.
- Recognizes, participates in, and adjusts to changing situations and work assignments.
"Fully Achieves Expectations" describes solid, fully competent performance.
Needs Improvement
- Performance does not consistently meet the requirements, standards, or objectives of the job.
- Needs improvement in one or more areas of consistent weakness. Problem areas should be monitored and documented.
- Requires guidance and direction to fully achieve/accomplish responsibilities and objectives.
Improvement is required for staff members to fully achieve expectations.
Unsatisfactory
Staff members must have been counseled regarding unsatisfactory performance to receive this rating.
- Performance is consistently below requirements and is Unsatisfactory.
- Performance meets few or none of the standards/objectives.
- Shows failure to follow directions and initiate improvement.
- Knowledge inadequate to retain job without improvement.
- Corrective action must be outlined and monitored.
Unsatisfactory is a rating that a staff member should not receive twice.
Narrative scales
Narrative scales, also known as qualitative or descriptive scales, are performance rating systems that rely on written feedback rather than numerical or quantitative performance ratings.
Instead of assigning numerical scores or predefined categories, evaluators using narrative scales provide detailed written assessments of an employee's performance.
Let's look at examples of a narrative scale from Williams College's Narrative performance development form .
For each of the outlined performance development competencies, they define 2 levels: Effective and Exceed Expectations.
Personal Leadership and Innovation
Effective: Effectively manages and utilizes time, is self-motivated, and approaches work from a service mindset. Identifies and resolves problems with an eye for quality and continuous improvement.
Exceeds expectations: Takes a strategic approach to organizational challenges. Uses innovative and creative ideas to solve problems and enhance the working environment. Actively evaluates new ways of working and is not afraid to make mistakes in productive ways.
Communication and collaboration.
Effective: Is responsive to the needs and expectations of customers. Demonstrates effective listening skills, proactively shares information, and effectively communicates. Works effectively as part of a team exhibits civility and respect. Solicits input and assistance from others.
Exceeds expectations: Consistently goes above and beyond to serve others and maintains a positive attitude. Asks questions and makes efforts to resolve misinformation and concerns. Hold themselves mutually accountable for the success of the team. Makes time to help colleagues, sharing knowledge and resources.

Graphic scales
A graphic scale for employee performance rating is a visual representation of a performance evaluation tool. It uses a graphical format (often a line or a bar) with labeled intervals to assess and communicate an employee's performance level. This type of scale provides a clear, visual, and easily understandable way to gauge performance.
Behaviorally-anchored rating scales
Behaviorally anchored rating scales (BARS) are a distinctive approach to employee performance assessment, offering a more comprehensive and precise measurement than conventional Likert or 1-5 scales.
This method employs a detailed evaluation framework, using various criteria, ranging from excellent to unsatisfactory, to assess employee performance.
The primary objective of BARS is to deliver highly accurate, objective, and dependable evaluations during performance appraisals. It achieves this by honing in on specific, observable behaviors directly relevant to job requirements and desired outcomes.

5️⃣ 5-Point performance rating scale examples
Let's see real-life examples of rating scales in action, starting with the 5-point scale.
The University of Maryland, Baltimore recommends a simple 5-point performance rating scale with the following 5 rating options:
- Outstanding: The employee's work consistently exceeded expectations.
- Above Standards: The majority of the employee's work exceeded expectations.
- Meets Standards : Performance fully met the established job expectations and may have periodically exceeded expectations.
- Below Standards : Performance met some of the job expectations but did not fully meet the established measures.
- Unsatisfactory: Performance generally failed to meet the established expectations or required frequent, close supervision and/or the redoing of work.

Their documentation further expands on the descriptions for each of the rating options. For example, this is the complete description for someone worthy of the "Above standards" rating:
Above standards
- Performance consistently exceeds the requirements needed to fulfill the principal duties, responsibilities, objectives, and expectations of the position.
- Frequently integrates a wide variety of technical, managerial, and other skills to effectively solve problems and carry out duties, responsibilities, and objectives beyond the expectations of the position; makes on-going improvements.
- Employee demonstrates proficiency in performing difficult and complex aspects of the job competently and thoroughly, including extra and unique tasks assigned.
- Quality of work is excellent; consistently exceeds performance expectations.
- Performance met all major aspects of expectations and exceeded requirements in several key areas. Performed the most difficult parts of the job competently and thoroughly.
- Adds value to the organization beyond what is expected; one of the key contributors within the organization and peer group. Contributes significant results of own initiative.
This 5-point rating scale example from Forbes Advisor also leverages numbers for faster results quantification.
- 5 (Outstanding): Performs significantly above the quality/quantity criteria for this role.
- 4 (Exceeds Expectations): Generally exceeds the quality/quantity criteria for this role.
- 3 (Meets Expectations): Meets the set criteria for the designated role.
- 2 (Needs Improvement): Didn't fully meet the set criteria for the designated role.
- 1 (Unacceptable): Performs significantly below set criteria.
🙋♀️ Behaviorally anchored rating scale examples
These detailed types of rating scales often require extra documentation to be prepared before applying them.
You can use any number of rating points as long as the main focus is on getting as many details as possible on an employee's behavior.
The following behaviorally anchored rating scale examples come from the State of Michigan. They differentiate between job groups, each group having a specific competency model. All groups share the same framework for a behaviorally anchored rating scale with 3 performance levels: needs improvement, meets expectations, and high-performing.
Group one refers to Technical, Office, Administrative Support, Paraprofessional, and Service Occupations (Non-Supervisory) roles. Their competency model consists of 16 competencies:
- adaptability;
- applied learning;
- building customer loyalty;
- communication;
- contributing to team success;
- decision making;
- initiating action;
- innovation;
- integrity/honesty;
- interpersonal skills;
- managing work;
- quality orientation;
- safety awareness;
- stress tolerance;
- valuing diversity and inclusion;
Group two refers to Business, Human Service, Scientific, and Engineering Professional Classes (Non-Supervisory) roles. Their competency model consists of 15 competencies :
- building strategic working relationships;
- building trust;
- continuous learning;
- customer focus;
- planning and organizing work;
- work standards;
Group three covers the competency model for managers , consisting of 15 competencies :
- communication
- technical/professional knowledge and skills;
- delegating responsibility;
- developing a successful team;
- aligning performance for success;
- managing conflict;
- facilitating change;
- building partnerships;
Let's look at how they define adaptability for the 3 categories of roles:
| Competency BARS Level | Technical, Office, Administrative Support Staff | Business, Human Service, Scientific Staff | Managers |
|---|---|---|---|
Now, let's take an extra BARS example and look at how they define the behavioral indicators for the managerial competency of developing a successful team :
- Often fails to build consensus in team thoughts and actions; key objectives are not understood by or acted upon by team members.
- Does not promote full team involvement in decisions; the leader makes all substantive decisions.
- Expects the team to solve problems but does not give enough guidance or support.
- Ignores dissension; doesn't attain full team participation; allows one or more team members to unduly influence others.
- Does not consider diversity of skills and perspectives in assembling and developing team.
Meets Expectations
- Brings individuals together who effectively work towards solving a problem or goal.
- Monitors team progress towards goals and regularly provides feedback to the team regarding progress.
- Actively involves the team in decision-making; gives the team credit for successes as well as responsibility for failures.
- Actively seeks ideas and involvement of team members in problem-solving and shares information on why decisions are made.
- Creates an environment where team members accept differences in approaches. Values the opinions of others and acts to promote the success of the entire team.
High Performing
- Leads teams that are highly effective in producing significant business results; teams are recognized within the organization for their ability to deliver results.
- Creates high-performing teams where team members regularly learn from each other and adapt team processes for improved team efficiency and outcomes.
- Highly effective in developing and sustaining a high level of team member commitment and "ownership" for decisions and results by team members.
- Conveys strong confidence in self and team; builds pride in the team and inspires team members to perform to their fullest.
- Insightfully diagnoses critical skills and capabilities needed by individuals or by the entire team and takes effective action to bring about needed improvement.
3️⃣ 3-Point performance rating scale examples
This University of Michigan rating scale example , for instance, sticks to a 3-point scale but further develops upon the exact criteria behind each point:
- Exceeded: The employee's performance far exceeded expectations due to exceptionally high quality of work performed in all essential areas of responsibility, resulting in an overall quality of work that was superior and either included the completion of a major goal or project, or made an exceptional or unique contribution in support of unit, department, or college objectives. This rating is achievable by any employee, though given infrequently.
- Achieved: The employee's performance consistently met expectations in all essential areas of responsibility, at times possibly exceeding expectations, and the quality of work overall was very good. The most critical annual goals were met. Typically demonstrates proficient knowledge, skills, and abilities for the required work.
- Not Achieved: The employee's performance did not consistently meet expectations and failed to meet expectations in one or more essential areas of responsibility, and/or one or more of the most critical goals were not met. The employee's work failed to meet the goals of the job function and generally falls short of performance goals, even though sometimes approaching goals. The employee provides minimal support to the contributions of the organization.

🔟 10 Point performance rating scale examples
While not as popular due to its extensiveness, a 10-point performance rating scale is a system where employees are assessed on a scale from 1 to 10, with each point on the scale corresponding to a different level of performance.
This type of scale allows for a higher degree of granularity in evaluating employee performance.

Here's an example of a 10-point performance rating scale along with corresponding descriptors:
1: Poor performance: Employee consistently falls far short of meeting performance standards. Significant improvement is needed.
2: Very weak: Employee's performance is consistently below what is expected. Immediate improvement is a must.
3: Weak: Employee's performance is below the expected level, but there are occasional instances of meeting expectations.
4: Below average: Employee consistently meets the expected performance standards, but there's room for refinement and growth.
5: Average: Employee consistently meets all performance standards satisfactorily.
6: Above average: Employee not only meets but consistently exceeds expectations.
7: Good: Employee consistently surpasses performance standards with some notable achievements.
8: Very good: Employee consistently exceeds expectations with significant achievements.
9: Excellent: Employee's performance is consistently exemplary, far surpassing all expectations.
10: Outstanding: Employee's performance is consistently exceptional, demonstrating a level of achievement far beyond what is expected.

🌟 Competency rating scale 1-5 examples
Competency rating scales help you evaluate employee performance by touching on specific competencies or skills. They prove particularly valuable in assessing whether a job candidate or current employee aligns with the requirements of their role.
These scales are especially useful for performance reviews when aiming to enhance training initiatives within your team or when considering a new hire or promotion. Customized to each specific job role, they gauge employee competencies in critical areas like adaptability, communication, problem-solving, and beyond.

Competencies ratings follow a five or four-point scale such as:
1 - Needs improvement
2 - Below expectations
3 - Meets expectations
4 - Exceeds expectations
5 - Expert (sets a new standard)
We know that many companies are wary of using numbered scales. To mitigate this issue, Berfu Ulusoy , our Learning and Development Manager at Zavvy , recommends ditching the numbers altogether and using a simple scale with labels for more clarity.
Here's a growth rating scale she recommends using:
- Developing: Making efforts to improve skills and knowledge.
- Expanding : Demonstrating growth and acquiring new competencies.
- Evolving: Continuously improving and adapting to challenges.
- Advancing: Making significant strides in personal and professional development.
- Transforming: Exhibiting exceptional growth, embracing change, and inspiring others.
➡️ Get our free guide to conducting competency-based performance appraisals and learn more about the latest methods of assessing employee skills and competencies .

✅ 5 Factors to consider when choosing the right rating scale for your teams
Now that you've got a good grasp on the performance rating scale options you have let's see what you need to take into account before picking one.

The feedback culture in your company
A culture that values positive feedback and honest communication can help create an environment where employees feel comfortable providing constructive feedback and trust that their opinions will be heard and respected.
By taking this into account, you can choose rating scales tailored to the specific needs of individuals in your team and ensure that your employees feel comfortable and supported in the feedback process. Additionally, a well-designed rating scale can encourage employees to provide meaningful, thoughtful feedback that can be used to help improve team performance.
Our expert, Berfu, notes that if you're not feeling comfortable using scales, you can stick to qualitative answers to open-ended questions:
"One method is giving your employees keywords like 'developing' or 'expanding' and asking them to include them when answering the questions. This way, it'll be easier for you to analyze and even quantify qualitative data."
The type of reviews needed
Are you only looking to get manager performance reviews? Or do you want to involve different team members in performance reviews?
If you want to extend performance ratings to the entire organization, Likert or 5-point scales are fairly easy and quick to use, so you can turn to them whenever you want to gather feedback from colleagues , clients, and collaborators. Plus, employees can even use them to self-rate their performance .

The types of role or industry you're in
Customer service roles may require different rating scales than those in a design or web development role. Further, certain industries may require different scales. Simply put, to measure performance accurately, you need the right scales that will support the diversity of criteria you want to test.
Let's go back to our two industry examples.
In a creative role, performance might be measured using criteria such as creativity, collaboration, and innovation.
In contrast, in a customer service environment, performance will be evaluated using criteria such as customer satisfaction, product knowledge, and responsiveness. The latter are easier to measure using quantitative scales like a 5-point system.
The scale's complexity
Qualitative review might require a more detailed rating scale that allows you to capture different aspects of the feedback, such as the quality of the work, the speed of delivery, and the overall customer experience.
On the opposite end, a quantitative review might require a simpler rating scale that focuses on the team's overall performance. Considering the type of reviews needed will help you choose the most suitable rating scale for your team.
Jo Taylor, Founder & MD at Let's Talk Talent , advocates for keeping past performance analysis simple:
"I like the 3 levels of High Performing, Performing, and Development. You could add in needs significant development if you wanted a fourth. With any description, be clear on what you're asking of people and how they can deliver against this. No one will ever have all High performing. Not even your CEO. So this enables you to have a much more nuanced conversation about where someone is developing but also where they're overperforming."
Training requirements and available resources
Training materials and possibilities are important to consider because they can determine the complexity of the scale for employee performance reviews.
Suppose your team doesn't have access to the right training materials or enough time to learn a complex rating system. In that case, a simpler scale may be more appropriate.

➡️ Regardless of your rating scale of choice, you can easily customize our free templates and get your reviews in motion as soon as possible.
🏆 8 Best practices for ensuring your performance rating scales drive clarity, consistency, and fairness

Use these eight core best practices when defining the rating scales for your performance review cycles:
- Write clear descriptors: Leave little room for ambiguity during employee performance reviews. All raters should have the exact same understanding of what each level means.

- Maintain consistent increments: The difference between each successive level should be consistent. So, not jumping from not meeting to barely meeting or exceeding. There should always be other levels in between.
- Include anchor behaviors or examples: This ensures a shared understanding of what performance at each level should look like.
- Keep a balanced scale: Stick to an equal number of positive and negative performance levels, so you're not purely using a numerical scale.
- Always add a neutral midpoint: This is especially valid for scales with odd points, as a neutral mid-point is useful for capturing average or expected performance.
- Be wary of the cultural aspects and language you use: With any performance review, avoid jargon and stay culturally neutral to ensure all points and explanations are understood consistently across diverse groups.
- Combine performance ratings with regular feedback sessions for comprehensive performance reviews: Consider adding a calibration step after getting the results from your scales. Stick to our list of recommended steps for holding a fair and productive performance calibration meeting .
- Train your managers to ensure consistency in performance ratings across departments: Personal biases can still creep through even when descriptions are super clear. You can avoid these by ensuring your entire leadership team is up to par with the correct rating standards.

➡️ Measure and boost performance with Zavvy
Regardless of the performance rating scale you opt for, Zavvy is your go-to partner for driving performance and growth.
Elevate your performance reviews with a highly flexible and customizable tool. You have complete power over:
- The types of feedback you want to collect (peer, self-evaluations, manager reviews).
- The anonymity of the input.
- The recurrence and timeline of your cycles.
- The kinds of questions you want to ask (qualitative or quantitative).
- The kinds of ratings you want to use.
- Whether you want to link the questions to your people's competency and career frameworks .
- And much, much more.
Gain valuable insights into your workforce by pinpointing high achievers, assessing talent distribution, populating your 9-box grid with accurate data, and identifying potential issues like toxic leadership and more!

With Zavvy, you can effortlessly acknowledge strong performance and establish tailored employee development plans to support your people's professional growth.
Want to get your managers ready for their next performance review? Our experts provide manager workshops and tailored consultations to ensure you set up your organization's ideal feedback and performance review process.
📅 Book a demo of our Zavvy feedback and performance rating suite today!

What is a disadvantage of behaviorally anchored rating scales?
One disadvantage of behaviorally anchored rating scales is that they can be time-consuming and challenging to create. It requires extensive research and analysis to determine the specific behaviors needed for the rating scale. Additionally, since the scale is based on a specific set of behaviors, it can limit the feedback that is provided to employees.
What is the best rating scale for the performance review process?
Managers often find the 5-point scale encompasses the entire spectrum of job performance, ranging from excellent to unsatisfactory. This scale offers a level of detail that provides managers with valuable insights into their employees' work, surpassing the granularity of a ten-point scale. Its simplicity makes it ideal for managers seeking a clear and efficient way to assess contributions, facilitating well-informed decisions regarding employee development and promotion plans.
Can one scale fit all roles within an organization?
No. One standardized scale might not be suitable for all roles within your organization. You need to make meaningful comparisons between managers, departments, roles, etc. However, while different departments or roles might need tailored scales, it's important to have a degree of consistency across the organization to enable broader talent management initiatives, such as succession planning.

Lorelei is Zavvy's Content Marketing Manager. She is always on the hunt for the latest HR trends, fresh statistics, and academic and real-life best practices to spread the word about creating better employee experiences.
Als Nächstes lesen

How it works
Transform your enterprise with the scalable mindsets, skills, & behavior change that drive performance.
Explore how BetterUp connects to your core business systems.
We pair AI with the latest in human-centered coaching to drive powerful, lasting learning and behavior change.
Build leaders that accelerate team performance and engagement.
Unlock performance potential at scale with AI-powered curated growth journeys.
Build resilience, well-being and agility to drive performance across your entire enterprise.
Transform your business, starting with your sales leaders.
Unlock business impact from the top with executive coaching.
Foster a culture of inclusion and belonging.
Accelerate the performance and potential of your agencies and employees.
See how innovative organizations use BetterUp to build a thriving workforce.
Discover how BetterUp measurably impacts key business outcomes for organizations like yours.
A demo is the first step to transforming your business. Meet with us to develop a plan for attaining your goals.

- What is coaching?
Learn how 1:1 coaching works, who its for, and if it's right for you.
Accelerate your personal and professional growth with the expert guidance of a BetterUp Coach.
Types of Coaching
Navigate career transitions, accelerate your professional growth, and achieve your career goals with expert coaching.
Enhance your communication skills for better personal and professional relationships, with tailored coaching that focuses on your needs.
Find balance, resilience, and well-being in all areas of your life with holistic coaching designed to empower you.
Discover your perfect match : Take our 5-minute assessment and let us pair you with one of our top Coaches tailored just for you.

Research, expert insights, and resources to develop courageous leaders within your organization.
Best practices, research, and tools to fuel individual and business growth.
View on-demand BetterUp events and learn about upcoming live discussions.
The latest insights and ideas for building a high-performing workplace.
- BetterUp Briefing
The online magazine that helps you understand tomorrow's workforce trends, today.
Innovative research featured in peer-reviewed journals, press, and more.
Founded in 2022 to deepen the understanding of the intersection of well-being, purpose, and performance
We're on a mission to help everyone live with clarity, purpose, and passion.
Join us and create impactful change.
Read the buzz about BetterUp.
Meet the leadership that's passionate about empowering your workforce.
For Business
For Individuals
31 examples of problem solving performance review phrases

Jump to section
You're doing great
You should think of improving
Tips to improve
Use these practical examples of phrases, sample comments, and templates for your performance review , 360-degree feedback survey, or manager appraisal.
The following examples not only relate to problem-solving but also conflict management , effective solutions, selecting the best alternatives, decision making , problem identification, analyzing effectively, and generally becoming an effective problem-solving strategist. Start using effective performance review questions to help better guide your workforce's development.
Problem solving appraisal comments: you're doing great
- You always maintain an effective dialogue with clients when they have technical problems. Being clear and articulate makes sure our customers' faults are attended to promptly.
- You constantly make sure to look beyond the obvious you never stop at the first answer. You’re really good at exploring alternatives. Well done!
- Keeping the supervisors and managers informed of status changes and requests is important. You’re really good at communicating the changes to the projects at all times. Keep it up!
- You stay cool and collected even when things aren’t going according to plan or up in the air. This is a great trait to possess. Well done!
- You’re excellent at giving an honest and logical analysis. Keep it up! Effectively diagnosing complex problems and reaching sustainable solutions is one of your strong points.
- Your ability to ability to make complex systems into simple ones is truly a unique skill to possess. Well done!
- You often identify practical solutions to every roadblock. You’re a real asset to the team! Great job.
- You always listen actively and attentively to make sure you understand what the exact problem is and you come up with solutions in an effective manner.
- You have an amazing ability to clearly explain options and solutions effectively and efficiently. Well done!
- When driving projects, you can shift to other areas comfortably and easily. making sure the project runs smoothly. Great job!

Problem solving performance review phrases: you should think of improving
- You always seem too overwhelmed when faced with multiple problems. Try to think of ways to make problems more manageable so that they can be solved in a timely and effective manner.
- Avoiding conflicts constantly with people is not a good idea as you will only build up personal frustration and nothing will be done to remedy the situation. Try to face people when there are problems and rectify problems when they occur.
- Don’t allow demanding customers to rattle your cage too much. If they become too demanding, take a step back, regulate your emotions , and try to make use of online support tools to help you rectify problems these tools can help a lot!
- It’s necessary that you learn from your past mistakes . You cannot keep making the same mistakes , as this is not beneficial to the company.
- You tend to ask the same questions over and over again. Try to listen more attentively or take notes when colleagues are answering!
- Providing multiple solutions in an indirect and creative approach will allow you to be more effective at problem-solving . if you struggle with this typically through viewing the problem in a new and unusual light.
- You fail to provide staff with the appropriate amount of structure and direction. They must know the direction you wish them to go in to achieve their goals .
- You need to be able to recognize repetitive trends to solve problems promptly.
- You tend to have problems troubleshooting even the most basic of questions. As a problem solver and customer support person, it’s imperative that you can answer these questions easily.
- Read through your training manual and make sure you fully understand it before attempting questions again.

Performance review tips to improve problem solving
- Try to complain less about problems and come up with solutions to the problems more often. Complaining is not beneficial to progression and innovation.
- As a problem solver, it’s important to be able to handle multiple priorities under short deadlines.
- You need to be able to effectively distinguish between the cause and the symptoms of problems to solve them in an efficient and timely manner.
- Try to anticipate problems in advance before they become major roadblocks down the road.
- Try to view obstacles as opportunities to learn and thrive at the challenge of solving the problem.
- Remember to prioritize problems according to their degree of urgency. It's important that you spend the majority of your time on urgent tasks over menial ones.
- When putting plans into place, stick to them and make sure they are completed.
- When solving problems, try to allocate appropriate levels of resources when undertaking new projects. It is important to become as efficient and as effective as possible.
- Try to learn to pace yourself when solving problems to avoid burnout . You’re a great asset to the team and we cannot afford to lose at this point.
- Meeting regularly with your staff to review results is vital to the problem-solving process.
- Staff that has regular check-ins understand what it is that is required of them, what they are currently achieving, and areas they may need to improve. Try to hold one-on-one meetings every week.
Enhance your problem-solving skills
Discover personalized coaching to navigate challenges effectively and boost your performance.
Madeline Miles
Madeline is a writer, communicator, and storyteller who is passionate about using words to help drive positive change. She holds a bachelor's in English Creative Writing and Communication Studies and lives in Denver, Colorado. In her spare time, she's usually somewhere outside (preferably in the mountains) — and enjoys poetry and fiction.
How a performance review template improves the feedback process
25 performance review questions (and how to use them), agile performance management: how to improve an agile team, 53 performance review examples to boost growth, 5 tactics for managing managers effectively — and why it matters, managers have a strong effect on team performance, for better or worse, how stanford executive education embraces vulnerability as a form of resilience, awakening human potential: developing people and driving performance in the new world of work, uk leaders develop future-minded skills with betterup, similar articles, 10 problem-solving strategies to turn challenges on their head, teamwork skills self-appraisal comments: 40 example phrases, your complete guide to self-assessments (with examples), 30 communication feedback examples, finding your version of success: 29 tips to accomplish your goals, 30 customer service review examples to develop your team, 37 innovation and creativity appraisal comments, 8 creative solutions to your most challenging problems, stay connected with betterup, get our newsletter, event invites, plus product insights and research..
3100 E 5th Street, Suite 350 Austin, TX 78702
- Platform Overview
- Integrations
- Powered by AI
- BetterUp Lead™
- BetterUp Manage™
- BetterUp Care®
- Sales Performance
- Diversity & Inclusion
- Case Studies
- Why BetterUp?
- About Coaching
- Find your Coach
- Career Coaching
- Communication Coaching
- Life Coaching
- News and Press
- Leadership Team
- Become a BetterUp Coach
- BetterUp Labs
- Center for Purpose & Performance
- Leadership Training
- Business Coaching
- Contact Support
- Contact Sales
- Privacy Policy
- Acceptable Use Policy
- Trust & Security
- Cookie Preferences
- Undergraduate Admission
- Graduate Admission
- Tuition & Financial Aid
- Communications
- Health Sciences and Human Performance
- Humanities and Sciences
- Music, Theatre, and Dance
- IC Resources
- Office of the President
- Ithaca College at a Glance
- Awards and Accolades
- Five-Year Strategic Plan
- Directories
- Course Catalog
- Undergraduate
Farewell Cara!

As Cara Cirino ‘22 prepares to embark on her new journey at New York University, the team in the Office of Admission would like to express our heartfelt gratitude for her invaluable contributions. Cara's dedication and vibrant spirit have been instrumental in enhancing our daily operations, from engaging prospective families to contributing to the success of our large-scale events. Her innovative approach to problem-solving and data analysis has significantly improved our outreach efforts, particularly in one of our key recruitment territories in lower New York State and Connecticut. Cara's positive attitude and readiness to tackle challenges have not only benefited our team but have also left a lasting impression on everyone she worked with. As she transitions to her new role, we are confident that the skills and experiences she has honed here will lead to even greater achievements. Please join us as we bid Cara a fond farewell, celebrate her accomplishments, and wish her every success in her future endeavors. Her last day on campus is June 22, and while we will miss her presence, we are excited to see the heights she will reach at NYU. Thank you, Cara, for your remarkable contribution and for being a cherished member of our team!

IMAGES
VIDEO
COMMENTS
Instrument The Scale for Problem Solving Skills in Mathematics (SPSSM) was developed by Uysal (2007) in order to -report instrument consists of 28 items scored on a 5-point Likert type scale, ranging between 1 (never) to 5 (always). The scale has three subscales; utting effort in solving problems -confidence about utilized in the pilot study of ...
The fact that PSI consists of items measuring the confidence in problem-solving skills and the personal ... scale, ranging from 1 = Strongly Agree to 6 = Strongly Disagree. A total score can be calculated as a general index of problem-solving appraisal that ranges from 32 to 192. Lower scores on each factor
5. Show flexibility and persist through frustrations; continue to revise a plan or process of approach in order to arrive at a viable solution. Identifya strategy that could be used to overcome an obstacle in problem solving. Make an attempt to reach a viable solution by applying a strategy. Make multiple.
Of the participants, 218 (52.4%) were female and 198 (47.6%) were male. The Scale for Problem Solving Skills in Mathematics was developed by Uysal (2007) in order to determine the level of school ...
These are problem solving skills, teamwork skills, and other soft skills such as responsibility, accountability, self management, recognition of and respect for people's ... rubrics may be in the form of a rating scale or a checklist. Quinlan (2006) contrasts the differences between rating scales and checklists. She says that rubrics are
large‐scale assessment of problem solving competency (e.g. Blech & Funke, 2005; Funke & Frensch, 2007; Greiff & Funke, 2008; Klieme, 2004; Klieme, Leutner, & ... Problem‐ solving skills are necessary to achieve more than a basic level of skill in dealing with such situations and there is evidence that skills additional to those involved in ...
of executive functioning successfully to engage in age-appropriate levels of day-to-day planning, problem-solving, and organization necessary for success in most learning environments. Self-report of Personality . In contrast to rating scales, self-report scales lend themselves well to recording what goes on in the inner world of
The positive problem solving orientation and skills subscale did not meet the rating scale diagnostic of monotonicity, requiring the collapse of rating scale categories 0 and 1. Fit statistics demonstrated all items of all three subscales met the Infit Mnsq criteria within the range from 0.7 to 1.3, with ZSTD ranging within ±2.0 ( Table 5 ).
The ability to solve real-world problems and to transfer problem-solving strategies from domain-specific to domain-general contexts and vice versa has been regarded an important competence students should develop during their education in school (Greiff et al. []; van Merriënboer []).In the context of large-scale assessments such as the PISA study problem solving competence is defined as the ...
This paper describes the development of the teacher rating scale of interpersonal problem solving ability. It is a teacher report measure of an adolescent's problem solving ability. The 40-item measure was structured into five subscales: Interpersonal problem behavior; Negative problem solving behavior; Rational problem solving behavior; Impulsive behavior; and Avoidance behavior. The scale ...
To that end, the Problem-solving Skill Scale was administered to 39 mathematics teachers from 21 schools, for a total of 1010 sixth, seventh, and eighth grade students.
Behavior rating scales have been validated as one useful method for meeting best-practice goals in school and research-based assessment. The primary purpose of this chapter is to provide a rationale and framework for the applications of rating scales within the problem-solving model. As part of a problem-solving approach, rating scale methods can be extended and applied to facilitate problem ...
The development of the mathematical problem-solving skills of the students across grades was observed based on the increase in the mean score. The problem-solving skills developed from grade 7 to grade 8. The students of grade 7 had a mean score of −0.04 while grade 8 students had the highest mean score of 0.03.
1 - Unacceptable. Phrases examples: Fails to identify and resolve problems in a timely manner. Lacks critical thinking skills necessary for effective problem-solving. Often creates additional issues when attempting to resolve problems. Demonstrates a consistent inability to resolve even basic issues.
The second measure is the Wasik Problem-Solving Rating Scale. It isa 20-item self-rating scale designed so that it can be completed by individuals with less than. ... measure the problem-solving skills of parents of young children. The instrument measures means-end problem-solving thinking as described by Spivack and Levine
The Problem Rating Scale for Outcomes is a method to evaluate client progress throughout the period of service. It consists of three five-point, Likert-type scales to measure the entire range of severity for the concepts of Knowledge, Behavior, and Status. Knowledge is defined as what the client knows, Behavior as what the client does, and ...
Subjective cognitive load (CL) rating scales are widely used in educational research. However, there are still some open questions regarding the point of time at which such scales should be applied. Whereas some studies apply rating scales directly after each step or task and use an average of these ratings, others assess CL only once after the whole learning or problem-solving phase. To ...
The problem-solving scale was constructed to have a mean score among OECD countries of 500, with about ... Level 6 corresponds to the highest level of problem-solving skills. Students with a proficiency score within the range of Level 1 are expected to complete most Level 1 tasks successfully, but are unlikely to be able to complete tasks ...
This type of scale allows for a higher degree of granularity in evaluating employee performance. Here's an example of a 10-point performance rating scale along with corresponding descriptors: 1: Poor performance: Employee consistently falls far short of meeting performance standards. Significant improvement is needed.
The following examples not only relate to problem-solving but also conflict management, effective solutions, selecting the best alternatives, decision making, problem identification, analyzing effectively, and generally becoming an effective problem-solving strategist. Start using effective performance review questions to help better guide your ...
The purpose of checklists, rating scales and rubrics is to: provide tools for systematic recording of observations. provide tools for self-assessment. provide samples of criteria for students prior to collecting and evaluating data on their work. record the development of specific skills, strategies, attitudes and behaviours necessary for ...
The researches revealed that teachers who were lack of communication skills would have problems in leading students (Katyal & Evers, 2004) since classroom management was correlated with problem ...
We analyzed the shortcomings of existing instruments and saw a need for a new rating scale. The aim of this publication is to describe the development process for, and evaluation of, a new rating scale. Methods: First, we developed the rating scale in 10 steps. Then, two raters evaluated the newly developed rating scale by rating 135 videotaped ...
Managers with good problem-solving skills can help ensure companies run smoothly and prosper. If you're a current manager or are striving to become one, read this guide to discover what problem-solving skills are and why it's important for managers to have them. Learn the steps of the problem-solving process, and explore seven skills that can ...
Cara's dedication and vibrant spirit have been instrumental in enhancing our daily operations, from engaging prospective families to contributing to the success of our large-scale events. Her innovative approach to problem-solving and data analysis has significantly improved our outreach efforts, particularly in one of our key recruitment ...