

Difference between transportation and assignment problems?
- Engineeringbro
- February 11, 2023
- March 10, 2024
- 3 mins read
- Post author: Engineeringbro
- Post published: February 11, 2023
- Post category: Blog
- Post comments: 0 Comments
lets understand the Difference between transportation and assignment problems?
Transportation problems and assignment problems are two types of linear programming problems that arise in different applications.
The main difference between transportation and assignment problems is in the nature of the decision variables and the constraints.
If you’re unable to see the whole table kindly convert the mobile view to the desktop view
|
| |
Assignment Problem | Minimization or maximization of the cost of transporting goods from one source to another | Maximization of the total profit or minimization of the total cost in assigning tasks to individuals |
Nature of problem | Involves transporting goods from sources to destinations | Involves assigning tasks to individuals |
Number of sources and destinations | Multiple sources and destinations | An equal number of sources and destinations |
Availability and demand | Each source and destination have a supply or demand value | Each task has only one individual who can perform it |
Decision variables | Amount of goods transported from each source to each destination | Binary variables indicate whether an individual is assigned a task or not |
Constraints | Capacity constraints on sources and demand constraints on destinations | Each individual can only perform one task |
Solution method | Transportation simplex method, northwest corner rule, Vogel’s approximation method | Hungarian algorithm, brute force method |
Example | Transporting goods from factories to warehouses | Assigning tasks to employees or jobs to machines |

Additional Different between Transportation and Assignment Problems are as follows :
Decision Variables:
In a transportation problem, the decision variables represent the flow of goods from sources to destinations. Each variable represents the quantity of goods transported from a source to a destination.
In contrast, in an assignment problem, the decision variables represent the assignment of agents to tasks. Each variable represents whether an agent is assigned to a particular task or not.
Constraints:
In a transportation problem, the constraints ensure that the supply from each source matches the demand at each destination and that the total flow of goods does not exceed the capacity of each source and destination.
In contrast, in an assignment problem, the constraints ensure that each task is assigned to exactly one agent and that each agent is assigned to at most one task.
Objective function:
The objective function in a transportation problem typically involves minimizing the total cost of transportation or maximizing the total profit of transportation.
In an assignment problem, the objective function typically involves minimizing the total cost or maximizing the total benefit of assigning agents to tasks.
In summary,
The transportation problem is concerned with finding the optimal way to transport goods from sources to destinations,
while the assignment problem is concerned with finding the optimal way to assign agents to tasks.
Both problems are important in operations research and have numerous practical applications.
Checkout Home page for more informative content and Follow us on facebook for more
Please Share This Share this content
- Opens in a new window
You Might Also Like

Domestic electrolux refrigeration system – Working, Components
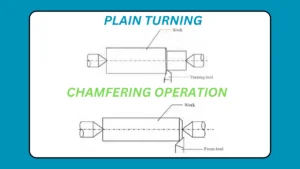
How to perform plain turning and chamfering operation

what is Chamfering machine
Leave a reply cancel reply.
- Transportation tableau
A guide to transportation problems ¶
Classic formulation ¶.
Let \(\mathcal{G}\) be a complete bipartite directed graph , with disjoint sets of vertices \(\mathcal{S}=\{s_i\}_{i=1}^{m}\) and \(\mathcal{D}=\{d_j\}_{j=1}^{n}\) interpreted respectively as supply nodes and demand nodes .
For all \(i=1,\dots,m,\;j=1,\dots,n\) let:
- \(c_{ij}\) represent the (unitary) transportation cost between \(s_i\) and \(d_j\) and \(C=\left(c_{ij}\right)\) the corresponding \(m\times n\) matrix
- \(x_{ij}\geq 0\) represent the amount of product transported between \(s_i\) and \(d_j\)
- \(S_i\) amount of available product ( supply ) at node \(s_i\)
- \(D_j\) amount of required product ( demand ) at node \(d_j\)
We then define the transportation problem as the linear programming problem of minimize the total transportation cost subject to supply and demand constraints i.e.,
\(\min\limits_{x}\sum\limits_{i=1}^m\sum\limits_{j=1}^n c_{ij}x_{ij}\) s.t.
- supply constraint : \(\sum\limits_{j=1}^n x_{ij}\leq S_i \;\;\forall i=1,\dots,m\)
- demand constraint : \(\sum\limits_{i=1}^m x_{ij}\geq D_j \;\;\forall j=1,\dots,n\)
Balancing ¶
We define two quantities that play a crucial role within transportation problem framework: total supply and total demand in the network, respectively expressed as \(S^*=\sum_{i=1}^m S_i\) and analogously \(D^*=\sum_{j=1}^n D_j\) . The problem is said to be balanced if \(S^* = D^*\) and unbalanced otherwise. In case of an unbalanced transportation problem, is convenient to distinguish two cases:
- if \(D^* > S^*\) the problem is infeasible because there is not enough supply to satisfy the given demand
- if \(S^* > D^*\) the problem is in turn feasible thanks to the excess supply which makes no harm to any of the constraints
Since in the former case is possible to state a priori that the problem will result in an infeasible one, is convenient to propose a general balancing method for a transportation problem:
- if \(D^* > S^*\) , we can add a dummy supply which is accountable for unmet demand i.e., a node \(s_{m+1}\) such that \(S_{m+1}=D^* - S^*\) . In this case, we are expanding costs matrix \(C\) by adding a new row. Each of its elements \(c_{m+1,j}\) will represent the cost penalty associated with unmet demand for demand node \(d_j\) . In a proper supply chain framework, this penalty can be thought as the financial loss for the unmet demand, as well as the buying-in cost for satisfying the (otherwise unmet) demand. In a costs minimization perspective, the higher is \(c_{m+1,j}\) the lower will be \(x_{m+1,j}\) : this means that we have a first way to influence the shape of the solution according to our (business) needs.
- if \(S^* > D^*\) , even if the problem would be feasible, is convenient to mirror the above technique by adding a dummy demand accountable for unexploited supply i.e., a node \(d_{n+1}\) such that \(D_{n+1}=S^* - D^*\) . Again, we are implicitly expanding costs matrix by adding a new column in which each element \(c_{i, n+1}\) will represent cost associated with unexploited supply. In a supply chain framework, this can be interpreted as storage cost for excess supply, and all the considerations made above about the relationship with \(x_{i,n+1}\) still hold.
In the following we will consider only balanced transportation problems, in which the balancing has might been restored with one of the above procedures. In particular, we will therefore consider both the constraints as equalities. For such a problem the following holds:
Theorem 1 ¶
Given a balanced transportation problem assigned over a complete bipartite directed graph \(\mathcal{G}\) , the problem admits at least one feasible solution.
Transportation tableau ¶

Transportation problem data are often summarized and visualized on a table called transportation tableau (see picture above). It basically consists in the costs matrix \(C\) , with the addition of a bottom row containing the demands and a right column containing the supplies. Moreover, it’s useful also to hold the decision variables \(x_{ij}\) as well as the total supply \(S^*\) and the total demand \(D^*\) .
Heuristics ¶
Based on the transportation tableau, several heuristics have been studied in order to find an initial basic feasible solution to the transportation problem. The most used are:
- North West Corner method
- Least Cost method
- Vogel’s Approximation method
They basically consist in algorithm than can be performed (also) by a human in order to match the problem constraints while distributing product amount amongst each \(x_{ij}\) (in a “Sudoku-like” approach) see here . Given an initial basic feasible solution, several techniques can be used to improve it in order to lower the corresponding objective function value (e.g. simplex method, evolutionary algorithms, Hungarian method).
We have seen that a classic transportation problem can be solved through several heuristics, even if possibly not in an optimal way. It’s anyway convenient, whenever possible, to approach it in a LP perspective, mostly to take advantages of all the linear programming techniques and libraries available.
The transportation problem can be approach as:
- a classic LP problem with continuous decision variables i.e., \(x_{ij}\in\mathbb{R}_{\geq 0}\) ;
- an ILP/MIP problem if \(x_{ij}\in\mathbb{N}\) i.e., if it’s more convenient to express the decision variables in terms of (integer) number of transports needed to satisfy the constraints. In this case, we must assume that the transportation costs do not depend on the amount of product transported along each route - to preserve linearity - and we also have to properly adjust objective function and constraints formulation to behave accordingly with the change in measurement units.
LP advantages ¶
Sensitivity analysis ¶.
LP formulation and implementation can guarantee several advantages in approaching a transportation problem.
One of them is the sensitivity analysis : defined \(x^*\) as the optimal solution (or the set of optimal solutions) and \(f\) the problem objective function, the sensitivity analysis leds to study changes in \(x^*\) and \(f(x^*)\) as functions of problem data.
For example, in the transportation problem framework, one of the sensitivity analysis goal is to answer to questions such as:
- how much and how costs decrease when supply increases of 1 unit?
- how much and how costs increase when demand increases of 1 unit?
Slack variables ¶
Another advantage of a LP approach is represented by slack variables , which enable the elastic relaxation of a given problem.
For example, we can consider the supply constraint \(\sum_{j=1}^n x_{ij}\leq S_i\) for a given supply node \(s_i\) . This constraint requires that the amount of product going out from \(s_i\) is at most equal to the node capacity i.e., \(S_i\) . Another way to monitor such a request is to keep track of the difference \(\nu_i:= \sum_{j=1}^n x_{ij} - S_i\) . If \(\nu_i\leq 0\) , the constraint has been observed, if \(\nu_i>0\) the constraint has been violated.
Having observed so, we can then relax the supply constraint by restating it as follows:
\(\sum\limits_{j=1}^n x_{ij}-\nu_i\leq S_i\)
where \(\nu_i\) is a decision variable taking values in \([0, U_i]\) - called slack variable - which objective is to soften the constraint possibly allowing to excess the given supply \(S_i\) .
The main purpose of slack variables is to locate infeasibility causes: if the resolution of the problem seems impossible, we can add one slack variable for each constraint, taking care of adding it also to the objective function multiplying it by a (big) penalty factor. After the successful resolution procedure, whenever a slack variable hits a nonzero value it means that, despite its penalty factor in the objective function, its usage has been crucial to the resolution itself i.e., in making the problem actually feasible.
In general:
- for a \(\leq\) constraint we should subtract the slack variable from the left side of the constraint i.e., where decision variables are located;
- for a \(\geq\) constraint we should add the slack variable to the left side of the constraint;
- for a \(=\) constraint we should split the slack variable in its positive and negative part and respectively add and subtract these components to the left side of the constraint;
- the slack variable must be added (if the goal is to minimize) / subtracted (if the goal is to maximize) from the objective function by multiplying it with a (big) penalty factor - to ensure its usage “only if needed”.
If any slack variable has been introduced and has been used in problem resolution, we must refactor the objective function value to restore its meaning with respect to the underlying business framework and units of measurements.
Multi-objective programming ¶
LP framework enables also to address multi-objective problems, in which for example we are interested in chase both \(\min f_1\) and \(\min f_2\) - we can consider both as minimization objectives thanks to the equivalence \(\max(f) = -\min(-f)\) . A more rigorous definition of chasing more objectives can be stated in a Pareto perspective: we could be interested in finding \(x^*\) such that, if there exists another \(x'\) such that \(f_1(x')<f_1(x^*)\) , then \(f_2(x')>f_2(x^*)\) . In other words our aim could be find a \(x^*\) which is Pareto-optimal i.e., a preferred solution such that any other candidate solution which significantly improves one of the objectives ends up worsening the other see here .
In such cases we can exploit one of the following techniques:
- relaxed formulation : address one of the two objectives as the “real” objective of our LP problem, by adding the relaxed version of the other within the problem constraints. For example \(\min f_1\) subject to \(f_2\leq \varepsilon\) where \(\varepsilon\) is an upper bound on \(f_2\) known a priori;
- elastic formulation : mix the objectives with a convex combination of parameters to encapsulate them into a single objective. For example \(\min\lambda f_1 + (1-\lambda)f_2\) where \(\lambda\in[0,1]\) controls the weight given to each of the original objectives;
- sequential formulation : solve a single objective problem with one of the two objectives, for example \(\min f_1\) finding \(x^*\) as optimal solution, and then approaching a second single objective problem, for example \(\min f_2\) , by adding a constraint to preserve the former optimality i.e., \(f_1(x)\leq f_1(x^*)\) .
Problem variations ¶
Transshipment nodes ¶.
The classic formulation can be extended to a more general case where the product goes from the supply nodes to the demand ones through one (resp. \(k\) ) layer of intermediary nodes, which is implicitly equivalent to change the underlying graph structure to the union of two (resp. \(k+1\) ) complete bipartite graphs which share one set of nodes. In such a case, we refer to the shared layer of nodes with \(\mathcal{T}=\{t_k\}_{k=1}^p\) and the problem objective will change as follows
\(\min\limits_{x}\sum\limits_{i=1}^m\sum\limits_{k=1}^p c_{ik}x_{ik} + \sum\limits_{k=1}^p\sum\limits_{j=1}^n c_{kj}x_{kj}\)
Both the supply and demand constraints must be changed accordingly (since no longer exists a direct connection between \(\mathcal{S}\) and \(\mathcal{D}\) ), and the transshipment constraint must be added in the following form
\(\sum\limits_{i=1}^m x_{ik}=\sum\limits_{j=1}^n x_{kj}\;,\;\;\forall k=1,\dots,p\)
assuming no storage is allowed within transshipment nodes.
Sortation centers ¶
The intermediaries of the middle layer can be interpreted also as sortation centers. In this case, a mixture between transportation problem and assignment problem better fits our needs: the classic transportation problem can be applied to the transportation of products between supply nodes and sortation centers, and then an assignment problem can be used to optimize the accountability of sortation centers with respect to final customer demands (this strategy is a simple yet good model of Amazon logistics).
In this case, the problem formulation can be changed as follows
\(\min\limits_{x,y}\sum\limits_{i=1}^m\sum\limits_{k=1}^p c_{ik}x_{ik} + \sum\limits_{k=1}^p\sum\limits_{j=1}^n c_{kj}y_{kj}\)
where the introduced new decision variables \(y_{kj}\in\{0,1\}\) are binary variables which represent the assignment of sortation between \(t_k\) and \(d_j\) , with corresponding sortation cost \(c_{kj}\) . The constraint of such a model are the following:
- supply constraint : \(\sum\limits_{k=1}^p x_{ik}\leq S_i \;\;\forall i=1,\dots,m\)
- sortation decoupling : \(\sum\limits_{k=1}^p y_{kj} = 1\;\;\forall j=1,\dots,n\)
- demand constraint : \(\sum\limits_{i=1}^m x_{ik} = \sum\limits_{j=1}^n y_{kj}\cdot D_j \;\;\forall k=1,\dots,p\)
Multi-commodity transportation ¶
In the case of a transportation problem which involves the transportation of more than one product, the “product” variable can be taken into account in the LP framework switching to a three-dimension tensor of decision variables \(x_{ijh}\) , each representing the amount of product \(p_h\) transported from \(s_i\) to \(d_j\) .
Duality ¶
For reference see this article .
An example ¶
Let us consider the following maximization problem \(\max 2x_1 + 3x_2\) s.t.
- \(4x_1 + 8x_2 \leq 12\;\;(1)\)
- \(2x_1 + x_2 \leq 3\;\;(2)\)
- \(3x_1 + 2x_2 \leq 4\;\;(3)\)
- \(x_1, x_2 \geq 0\;\;(4)\)
Thanks to nonnegativity constraint (4), we can observe for example that the objective function has an upper bound given by the left side of (1): this ensures that the objective function is bounded by 12. Similarly, the same holds dividing the left side of (1) by 2: we have then a better upper bound on the objective function i.e., 6: this is the inspiration for the following discussion.
Given \(f\) the objective function of our LP problem, is then possible to write \(f\) as a linear combination of variables \(x_j\) i.e., \(f(x_1,\dots,x_n)=\sum_{j=1}^nc_jx_j\) , and the same holds for the left side of each constraint, which can be represented by a function \(g_i\) such that \(g_i(x_1,\dots,x_n)=\sum_{j=1}^na_{ij}x_j\leq b_i\) . As in the above example, we are then interested in finding a linear combination of the given constraints which constitutes an upper bound on \(f\) i.e., \(f\leq\sum_{j=1}^nd_jx_j\leq M\) where \(d_j\geq c_j\) for all \(j=1,\dots, n\) . In the example, we are looking for a combination
\(d_1x_1 + d_2x_2\leq M\)
where \(d_1\geq 2\) and \(d_2\geq 3\) .
For doing so, we can consider a linear combination \(\sum_{j=1}^nd_j(y_1,\dots,y_p)x_j=\sum_{i=1}^py_ig_i(x_1,\dots,x_n)\leq\sum_{i=1}^pb_iy_i=M\) where \(y_i\geq 0\) are brand new variables linked with the original constraints. In the example, the linear combination is
\(y_1\left(4x_1 + 8x_2\right) + y_2\left(2x_1 + x_2\right) + y_3\left(3x_1 + 2x_2\right) \leq 12y_1 + 3y_2 + 4y_3\)
which correspondes to
\(\left(4y_1+2y_2+3y_3\right)x_1 + \left(8y_1+y_2+2y_3\right)x_2\leq 12y_1 + 3y_2 + 4y_3\)
As per the intro of this section, our goal is to find the best possible upper bound on \(f\) i.e., to lower as much as we can the upper bound \(M\) which controls \(f\) from above while respecting the constraints \(d_j\geq c_j\) for all \(j=1,\dots,n\) . We have then implicitly defined a new LP problem, corresponding to the original one, i.e. \(\min 12y_1 + 3y_2 + 4y_3\) s.t.
- \(4y_1+2y_2+3y_3 \geq 2\;\;(1)\)
- \(8y_1+y_2+2y_3 \geq 3\;\;(2)\)
- \(y_1, y_2, y_3 \geq 0\;\;(3)\)

Dual problem ¶
We have just figured out that a minimization problem corresponds in a “natural way” to a maximization one, and viceversa. In general we have that to a minimization problem \(\min b^Ty\) s.t.
- \(A^Ty\geq c\)
- \(y\geq 0\)
corresponds a maximization problem \(\max c^Tx\) s.t.
- \(Ax\leq b\)
- \(x\geq 0\)
Given the privileged perspective of the transportation problem framework (minimization), we will call the former primal problem \(\mathfrak{P}\) and the latter its dual problem \(\mathfrak{D}\) .
Theorem 2 ¶
Any feasible solution of \(\mathfrak{D}\) is a lower bound on the objective function of \(\mathfrak{P}\) .
Theorem 3 ¶
One of the following holds:
- both \(\mathfrak{P}\) and \(\mathfrak{D}\) are infeasible;
- \(\mathfrak{P}\) is unbounded and \(\mathfrak{D}\) is infeasible;
- \(\mathfrak{P}\) is infeasible and \(\mathfrak{D}\) is unbounded;
- both \(\mathfrak{P}\) and \(\mathfrak{D}\) are feasible. Furthermore, for any \(y^*\) solution of \(\mathfrak{P}\) and \(x^*\) solution of \(\mathfrak{D}\) , the equation \(b^Ty^*=c^Tx^*\) holds, which means that \(\min\mathfrak{P}=\max\mathfrak{D}\) .
Transportation dual problem ¶
A possible formulation of the dual problem of the (primal) classic transportation problem defined above, with equalities constraints, is the following \(\max\sum\limits_{j=1}^nD_jv_j-\sum\limits_{i=1}^mS_iu_i\) s.t. \(v_j-u_i\leq c_{ij}\)
To understand and interpret this dual problem, let us refer to this notes .
Consider the need of transportation expressed by the business stakeholders and modeled with the primal problem.
Imagine now that the business wants to outsource the transportation and finds an external company which offers such a service in a particular way: it offers to buy product at price \(u_i\) at each supply nodes, transport it and resell the same amount at demand nodes at price \(v_j\) . Since the original transportation cost from \(s_i\) to \(d_j\) was \(c_{ij}\) , from a cost perspective the business should only ensure that \(v_j - u_i\) is lower than \(c_{ij}\) : the dual constraint represents this condition. From the external company point of view, it represents a condition to be matched to make the proposal appealing for the customer (our business).
The dual objective function represents the net revenue of the external company in managing transportation along the network while satisfying customer constraints in terms of supply and demand.
Extensions to other graph structures ¶
This section goal is to discuss the following question: what happens to Theorem 1 if \(\mathcal{G}\) is not a complete bipartite graph anymore? Or, in other words, which are minimal balancing actions needed to ensure problem feasibility at the change of the underlying graph structure?
This is crucial because in a given business framework not all routes between \(\mathcal{S}\) and \(\mathcal{D}\) might be admissible. In such a case, graph connectivity can be “reduced” and therefore the problem could reveals to be infeasible subject to the given constraint.
Theorem 4 ¶
Consider a feasible transportation problem assigned over a bipartite directed graph \(\mathcal{G}\) . For each demand node \(d_j\) let \(\mathcal{S}^j\) be the set of indices of supply nodes adjacent to \(d_j\) . Then we have
\(\sum\limits_{i\in\mathcal{S}^j} S_i\geq D_j\)
This theorem provides a necessary condition to be checked in order to ensure feasibility for a transportation problem assigned over a generic bipartite graph: the sum of supplies of supply nodes adjacent to a given demand node must be at least equal to the demand of that node. This is a necessary condition which partially overcomes the possibly “insufficient” graph connectivity.
Unfortunately, since Theorem 1 does not hold if \(\mathcal{G}\) isn’t complete and Theorem 4 gives only a necessary condition, we are still without a set of sufficient conditions for feasibility of a transportation problem assigned over a generic bipartite directed graph. Given the relationship between graph structure and supply-demand constraints, any useful condition must take into account the flow of product that can be assigned over the network ( max-flow connectivity , min-cut connectivity , etc.).
A custom heuristics ¶
In order to solve a transportation problem over a “generic” graph and to overcome the lack of a proper Theorem to ensure feasibility, a custom heuristics to “balance” the given problem before submitting it to the actual solver is below.
In particular, we search for \(\mathcal{D}^i\) (defined similarly to \(\mathcal{S}^j\) ) sets for each \(s_i\) and define the maximal set of suppliers adjacent to nodes in \(\mathcal{D}^i\) , denoting this set as \(\mathcal{S}(\mathcal{D}^i)\) . Then we refer to supplier nodes in \(\mathcal{S}(\mathcal{D}^i)\) as critical suppliers in the following cases:
- if \(\left|\mathcal{D}^i\right|=1\) ;
- if \(\left|\mathcal{D}^i\right|=2\) and \(\left|\mathcal{S}(\mathcal{D}^i)\right|=1\) .
We then sum up the supply of all the critical suppliers and create a dummy supply node, adjacent to all demand nodes , accountable for this quantity: this helps preventing the unattainability of the critical suppliers, which might affect problem feasibility.
Resources ¶
- TP in Scipbook
- Min cost flow problem by OR-tools
- TP heuristics
- OR for programmers
Copyright © 2003 by Robert Fourer, David M. Gay and Brian W. Kernighan





IMAGES
VIDEO
COMMENTS
7. Identify the relationship between assignment problems and transportation problems. 8. Formulate a spreadsheet model for an assignment problem from a description of the problem. 9. Do the same for some variants of assignment problems. 10. Give the name of an algorithm that can solve huge assignment problems that are well
The transportation problem is concerned with finding the optimal way to transport goods from sources to destinations, while the assignment problem is concerned with finding the optimal way to assign agents to tasks. Both problems are important in operations research and have numerous practical applications.
Transportation Problem deals with the optimal distribution of goods or resources from multiple sources to multiple destinations. While Assignment Problem deals with allocating tasks, jobs, or resources one-to-one. These LPP methods are used for cost minimization, resource allocation, supply chain management, workforce planning, facility ...
We then define the transportation problem as the linear programming problem of minimize the total transportation cost subject to supply and demand constraints i.e., min x ∑ i = 1 m ∑ j = 1 n c i j x i j s.t. supply constraint : ∑ j = 1 n x i j ≤ S i ∀ i = 1, …, m. demand constraint : ∑ i = 1 m x i j ≥ D j ∀ j = 1, …, n.
Identify the relationship between assignment problems and transportation problems. Formulate a spreadsheet model for an assignment problem from a description of the problem. Do the same for some variants of assignment problems. Give the name of an algorithm that can solve huge assignment problems that are well beyond the scope of Solver.
In this video, we discuss the introduction of an Assignment problem and the mathematical representation of the Assignment problem.Link For Complete Playlist ...
transportation problem. We won't even try showing what it would be like to type all of these constraints into an. AMPL. model file. Clearly we want to set up a general model to deal with this prob-lem. 3.2 An AMPL model for the transportation problem. Two fundamental sets of objects underlie the transportation problem: the sources or
Transportation Problem •To solve the transportation problem by its special purpose algorithm, it is required that the sum of the supplies at the sources equal the sum of the demands at the destinations. If the total supply is greater than the total demand, a dummy destination is added with demand equal to the excess supply, and shipping costs
The Simplex Method for Transportation Problems. Illustrative Examples and a Note on Degeneracy. The Simplex Tableau Associated with a Transportation Tableau. The Assignment Problem: (Kuhn's) Hungarian Algorithm. Alternating Path Basis Algorithm for Assignment Problems. A Polynomial-Time Successive Shortest Path Approach for Assignment Problems
Solve maximization transportation problems, unbalanced problems, and problems with prohibited routes. Solve aggregate planning problems using the transportation model. Formulate a transshipment problem as a linear programming model. Solve transshipment problems with Excel. Formulate an assignment problem as a linear programming model. Use the ...
Traffic assignment considers which paths are to be selected and the amount of traffic using these paths (if more than one unit). For simple problems, a single path will be selected, while for complex problems, several paths could be used. Factors behind the choice of traffic assignment may include cost, time, or the number of connections.
Figure 8: Constructing a transportation problem 4.3.2 Mathematical model of a transportation problem Before we discuss the solution of transportation problems we will introduce the notation used to describe the transportation problem and show that it can be formulated as a linear programming problem. We use the following notation; x
Transshipment problems can be converted to larger transportation problems and solved by a special transportation program. Transshipment problems can also be solved by general purpose linear programming codes. The network representation for a transshipment problem with two sources, three intermediate nodes,
Á "Á c
In the transport task, the vertices are cities, and the edges represent available roads. 2. Review of transportation problems 2.1. Basic transportation problem This is the simplest form of the transportation problem, where the goal is to find the cheapest way to transport a given amount of goods from a set of sources to a set of destinations.
similarities between transportation and transshipment. based on LP network flow problems transporting materials minimizing costs supply and demand do not have to be equal involve choices of location that do not have to be the same number. differences between transportation and assignment model.
Step 1/2. The similarity between the transportation problem and the assignment problem lies in their basic structure and objective. Both problems are special cases of linear programming problems that involve allocating resources from one set of elements (sources) to another set of elements (destinations) in an optimal manner.
32. The similarity between Assignment Problem and Transportation Problem is: (a) Both are rectangular matrices, (b) Both are square matrices, (c) Both can be solved by graphical method, (d) Both have objective function and non-negativity constraints. ( ) 680 Operations Research33. The following statement applies to both ...
Transportation Problem: Assignment Problem: 1. This is about reducing cost of transportation merchandise: 1. This is about assigning finite sources to finite destinations where only one destination is allotted for one source with minimum cost: 2. Number of sources and number of demand need not be equal: 2.
Transportation Model Assignment Model; The problem may have a rectangular matrix or a square matrix. The assignment algorithm can not be used to solve the transportation model. The rows and columns may have any number of allocations depending on the rim conditions. The rows and columns must have one-to-one allocation.
The assignment problem is said to be balanced if it is a _____. Choose the correct alternative : In an assignment problem if number of rows is greater than number of columns then. The objective of an assignment problem is to assign _____. In an assignment problem, if number of column is greater than number of rows, then a dummy column is added.
Assignment problems involve assigning a set of tasks or jobs to a set of workers or machines, with the objective of minimizing the total cost or time required to complete all tasks. This is typically done by creating a matrix of costs or times for each worker-machine combination, and then finding the optimal assignment that minimizes the total ...
1. answer below ». The similarity between Assignment Problem and Transportation Problem is: (a) Both are rectangular matrices, (b) Both are square matrices, (c) Both can be solved by graphical method, (d) Both have objective function and non-negativity constraints. The total opportunity cost matrix is obtained by doing: (a) Row operation on ...