the assignment problem is solved by dash

• Data Structures
• Linked List
• Binary Tree
• Binary Search Tree
• Segment Tree
• Disjoint Set Union
• Fenwick Tree
• Red-Black Tree
• Advanced Data Structures

Hungarian Algorithm for Assignment Problem | Set 1 (Introduction)

• Hungarian Algorithm for Assignment Problem | Set 2 (Implementation)
• Introduction to Exact Cover Problem and Algorithm X
• Greedy Approximate Algorithm for Set Cover Problem
• Job Assignment Problem using Branch And Bound
• Implementation of Exhaustive Search Algorithm for Set Packing
• Channel Assignment Problem
• Chocolate Distribution Problem | Set 2
• Transportation Problem | Set 1 (Introduction)
• OLA Interview Experience | Set 11 ( For Internship)
• Top 20 Greedy Algorithms Interview Questions
• Job Sequencing Problem - Loss Minimization
• Prim's Algorithm (Simple Implementation for Adjacency Matrix Representation)
• Data Structures and Algorithms | Set 21
• Adobe Interview Experience | Set 55 (On-Campus Full Time for MTS profile)
• Amazon Interview Experience | Set 211 (On-Campus for Internship)
• OYO Rooms Interview Experience | Set 3 (For SDE-II, Gurgaon)
• C# Program for Dijkstra's shortest path algorithm | Greedy Algo-7
• Algorithms | Dynamic Programming | Question 7
• Amazon Interview | Set 46 (On-campus for Internship)

• For each row of the matrix, find the smallest element and subtract it from every element in its row.
• Do the same (as step 1) for all columns.
• Cover all zeros in the matrix using minimum number of horizontal and vertical lines.
• Test for Optimality: If the minimum number of covering lines is n, an optimal assignment is possible and we are finished. Else if lines are lesser than n, we haven’t found the optimal assignment, and must proceed to step 5.
• Determine the smallest entry not covered by any line. Subtract this entry from each uncovered row, and then add it to each covered column. Return to step 3.

Try it before moving to see the solution

Explanation for above simple example:

  An example that doesn’t lead to optimal value in first attempt: In the above example, the first check for optimality did give us solution. What if we the number covering lines is less than n.

Time complexity : O(n^3), where n is the number of workers and jobs. This is because the algorithm implements the Hungarian algorithm, which is known to have a time complexity of O(n^3).

Space complexity :   O(n^2), where n is the number of workers and jobs. This is because the algorithm uses a 2D cost matrix of size n x n to store the costs of assigning each worker to a job, and additional arrays of size n to store the labels, matches, and auxiliary information needed for the algorithm.

In the next post, we will be discussing implementation of the above algorithm. The implementation requires more steps as we need to find minimum number of lines to cover all 0’s using a program. References: http://www.math.harvard.edu/archive/20_spring_05/handouts/assignment_overheads.pdf https://www.youtube.com/watch?v=dQDZNHwuuOY

Please Login to comment...

Similar reads.

• Mathematical

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Procedure, Example Solved Problem | Operations Research - Solution of assignment problems (Hungarian Method) | 12th Business Maths and Statistics : Chapter 10 : Operations Research

Chapter: 12th business maths and statistics : chapter 10 : operations research.

Solution of assignment problems (Hungarian Method)

First check whether the number of rows is equal to the numbers of columns, if it is so, the assignment problem is said to be balanced.

Step :1 Choose the least element in each row and subtract it from all the elements of that row.

Step :2 Choose the least element in each column and subtract it from all the elements of that column. Step 2 has to be performed from the table obtained in step 1.

Step:3 Check whether there is atleast one zero in each row and each column and make an assignment as follows.

Step :4 If each row and each column contains exactly one assignment, then the solution is optimal.

Example 10.7

Solve the following assignment problem. Cell values represent cost of assigning job A, B, C and D to the machines I, II, III and IV.

Here the number of rows and columns are equal.

∴ The given assignment problem is balanced. Now let us find the solution.

Step 1: Select a smallest element in each row and subtract this from all the elements in its row.

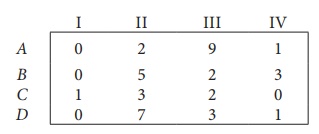
Look for atleast one zero in each row and each column.Otherwise go to step 2.

Step 2: Select the smallest element in each column and subtract this from all the elements in its column.

Since each row and column contains atleast one zero, assignments can be made.

Step 3 (Assignment):

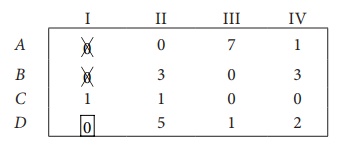
Thus all the four assignments have been made. The optimal assignment schedule and total cost is

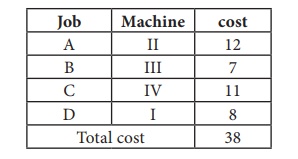
The optimal assignment (minimum) cost

Example 10.8

Consider the problem of assigning five jobs to five persons. The assignment costs are given as follows. Determine the optimum assignment schedule.

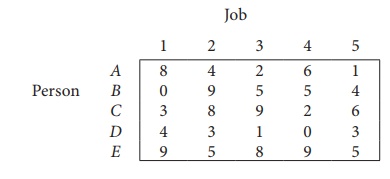
∴ The given assignment problem is balanced.

Now let us find the solution.

The cost matrix of the given assignment problem is

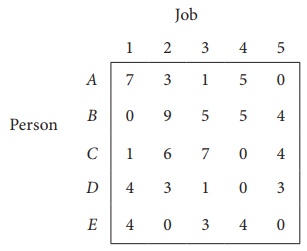
Column 3 contains no zero. Go to Step 2.

Thus all the five assignments have been made. The Optimal assignment schedule and total cost is

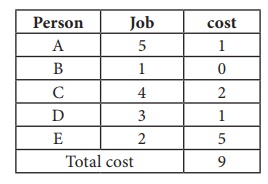
The optimal assignment (minimum) cost = ` 9

Example 10.9

Solve the following assignment problem.

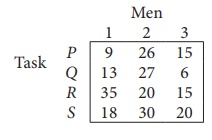
Since the number of columns is less than the number of rows, given assignment problem is unbalanced one. To balance it , introduce a dummy column with all the entries zero. The revised assignment problem is

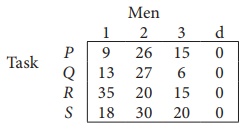
Here only 3 tasks can be assigned to 3 men.

Step 1: is not necessary, since each row contains zero entry. Go to Step 2.

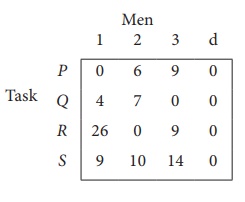
Step 3 (Assignment) :

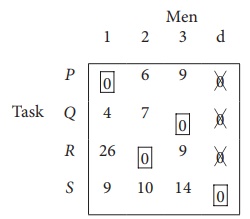
Since each row and each columncontains exactly one assignment,all the three men have been assigned a task. But task S is not assigned to any Man. The optimal assignment schedule and total cost is

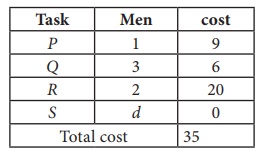
The optimal assignment (minimum) cost = ₹ 35

Related Topics

Privacy Policy , Terms and Conditions , DMCA Policy and Compliant

Copyright © 2018-2024 BrainKart.com; All Rights Reserved. Developed by Therithal info, Chennai.

Reset password New user? Sign up

Existing user? Log in

Hungarian Maximum Matching Algorithm

Already have an account? Log in here.

The Hungarian matching algorithm , also called the Kuhn-Munkres algorithm, is a \(O\big(|V|^3\big)\) algorithm that can be used to find maximum-weight matchings in bipartite graphs , which is sometimes called the assignment problem . A bipartite graph can easily be represented by an adjacency matrix , where the weights of edges are the entries. Thinking about the graph in terms of an adjacency matrix is useful for the Hungarian algorithm.

A matching corresponds to a choice of 1s in the adjacency matrix, with at most one 1 in each row and in each column.

The Hungarian algorithm solves the following problem:

In a complete bipartite graph \(G\), find the maximum-weight matching. (Recall that a maximum-weight matching is also a perfect matching.)

This can also be adapted to find the minimum-weight matching.

Say you are having a party and you want a musician to perform, a chef to prepare food, and a cleaning service to help clean up after the party. There are three companies that provide each of these three services, but one company can only provide one service at a time (i.e. Company B cannot provide both the cleaners and the chef). You are deciding which company you should purchase each service from in order to minimize the cost of the party. You realize that is an example of the assignment problem, and set out to make a graph out of the following information: \(\quad\) Company\(\quad\) \(\quad\) Cost for Musician\(\quad\) \(\quad\) Cost for Chef\(\quad\) \(\quad\) Cost for Cleaners\(\quad\) \(\quad\) Company A\(\quad\) \(\quad\) $108\(\quad\) \(\quad\) $125\(\quad\) \(\quad\) $150\(\quad\) \(\quad\) Company B\(\quad\) \(\quad\) $150\(\quad\) \(\quad\) $135\(\quad\) \(\quad\) $175\(\quad\) \(\quad\) Company C\(\quad\) \(\quad\) $122\(\quad\) \(\quad\) $148\(\quad\) \(\quad\) $250\(\quad\) Can you model this table as a graph? What are the nodes? What are the edges? Show Answer The nodes are the companies and the services. The edges are weighted by the price.

What are some ways to solve the problem above? Since the table above can be thought of as a \(3 \times 3\) matrix, one could certainly solve this problem using brute force, checking every combination and seeing what yields the lowest price. However, there are \(n!\) combinations to check, and for large \(n\), this method becomes very inefficient very quickly.

The Hungarian Algorithm Using an Adjacency Matrix

The hungarian algorithm using a graph.

With the cost matrix from the example above in mind, the Hungarian algorithm operates on this key idea: if a number is added to or subtracted from all of the entries of any one row or column of a cost matrix, then an optimal assignment for the resulting cost matrix is also an optimal assignment for the original cost matrix.

The Hungarian Method [1] Subtract the smallest entry in each row from all the other entries in the row. This will make the smallest entry in the row now equal to 0. Subtract the smallest entry in each column from all the other entries in the column. This will make the smallest entry in the column now equal to 0. Draw lines through the row and columns that have the 0 entries such that the fewest lines possible are drawn. If there are \(n\) lines drawn, an optimal assignment of zeros is possible and the algorithm is finished. If the number of lines is less than \(n\), then the optimal number of zeroes is not yet reached. Go to the next step. Find the smallest entry not covered by any line. Subtract this entry from each row that isn’t crossed out, and then add it to each column that is crossed out. Then, go back to Step 3.

Solve for the optimal solution for the example in the introduction using the Hungarian algorithm described above. Here is the initial adjacency matrix: Subtract the smallest value in each row from the other values in the row: Now, subtract the smallest value in each column from all other values in the column: Draw lines through the row and columns that have the 0 entries such that the fewest possible lines are drawn: There are 2 lines drawn, and 2 is less than 3, so there is not yet the optimal number of zeroes. Find the smallest entry not covered by any line. Subtract this entry from each row that isn’t crossed out, and then add it to each column that is crossed out. Then, go back to Step 3. 2 is the smallest entry. First, subtract from the uncovered rows: Now add to the covered columns: Now go back to step 3, drawing lines through the rows and columns that have 0 entries: There are 3 lines (which is \(n\)), so we are done. The assignment will be where the 0's are in the matrix such that only one 0 per row and column is part of the assignment. Replace the original values: The Hungarian algorithm tells us that it is cheapest to go with the musician from company C, the chef from company B, and the cleaners from company A. We can verify this by brute force. 108 + 135 + 250 = 493 108 + 148 + 175 = 431 150 + 125 + 250 = 525 150 + 148 + 150 = 448 122 + 125 + 175 = 422 122 + 135 + 150 = 407. We can see that 407 is the lowest price and matches the assignment the Hungarian algorithm determined. \(_\square\)

The Hungarian algorithm can also be executed by manipulating the weights of the bipartite graph in order to find a stable, maximum (or minimum) weight matching. This can be done by finding a feasible labeling of a graph that is perfectly matched, where a perfect matching is denoted as every vertex having exactly one edge of the matching.

How do we know that this creates a maximum-weight matching?

A feasible labeling on a perfect match returns a maximum-weighted matching. Suppose each edge \(e\) in the graph \(G\) connects two vertices, and every vertex \(v\) is covered exactly once. With this, we have the following inequality: \[w(M’) = \sum_{e\ \epsilon\ E} w(e) \leq \sum_{e\ \epsilon\ E } \big(l(e_x) + l(e_y)\big) = \sum_{v\ \epsilon\ V} l(v),\] where \(M’\) is any perfect matching in \(G\) created by a random assignment of vertices, and \(l(x)\) is a numeric label to node \(x\). This means that \(\sum_{v\ \epsilon\ V}\ l(v)\) is an upper bound on the cost of any perfect matching. Now let \(M\) be a perfect match in \(G\), then \[w(M) = \sum_{e\ \epsilon\ E} w(e) = \sum_{v\ \epsilon\ V}\ l(v).\] So \(w(M’) \leq w(M)\) and \(M\) is optimal. \(_\square\)

Start the algorithm by assigning any weight to each individual node in order to form a feasible labeling of the graph \(G\). This labeling will be improved upon by finding augmenting paths for the assignment until the optimal one is found.

A feasible labeling is a labeling such that

\(l(x) + l(y) \geq w(x,y)\ \forall x \in X, y \in Y\), where \(X\) is the set of nodes on one side of the bipartite graph, \(Y\) is the other set of nodes, \(l(x)\) is the label of \(x\), etc., and \(w(x,y)\) is the weight of the edge between \(x\) and \(y\).

A simple feasible labeling is just to label a node with the number of the largest weight from an edge going into the node. This is certain to be a feasible labeling because if \(A\) is a node connected to \(B\), the label of \(A\) plus the label of \(B\) is greater than or equal to the weight \(w(x,y)\) for all \(y\) and \(x\).

A feasible labeling of nodes, where labels are in red [2] .

Imagine there are four soccer players and each can play a few positions in the field. The team manager has quantified their skill level playing each position to make assignments easier.

How can players be assigned to positions in order to maximize the amount of skill points they provide?

The algorithm starts by labeling all nodes on one side of the graph with the maximum weight. This can be done by finding the maximum-weighted edge and labeling the adjacent node with it. Additionally, match the graph with those edges. If a node has two maximum edges, don’t connect them.

Although Eva is the best suited to play defense, she can't play defense and mid at the same time!

If the matching is perfect, the algorithm is done as there is a perfect matching of maximum weights. Otherwise, there will be two nodes that are not connected to any other node, like Tom and Defense. If this is the case, begin iterating.

Improve the labeling by finding the non-zero label vertex without a match, and try to find the best assignment for it. Formally, the Hungarian matching algorithm can be executed as defined below:

The Hungarian Algorithm for Graphs [3] Given: the labeling \(l\), an equality graph \(G_l = (V, E_l)\), an initial matching \(M\) in \(G_l\), and an unmatched vertex \(u \in V\) and \(u \notin M\) Augmenting the matching A path is augmenting for \(M\) in \(G_l\) if it alternates between edges in the matching and edges not in the matching, and the first and last vertices are free vertices , or unmatched, in \(M\). We will keep track of a candidate augmenting path starting at the vertex \(u\). If the algorithm finds an unmatched vertex \(v\), add on to the existing augmenting path \(p\) by adding the \(u\) to \(v\) segment. Flip the matching by replacing the edges in \(M\) with the edges in the augmenting path that are not in \(M\) \((\)in other words, the edges in \(E_l - M).\) Improving the labeling \(S \subseteq X\) and \(T \subseteq Y,\) where \(S\) and \(T\) represent the candidate augmenting alternating path between the matching and the edges not in the matching. Let \(N_l(S)\) be the neighbors to each node that is in \(S\) along edges in \(E_l\) such that \(N_l(S) = \{v|\forall u \in S: (u,v) \in E_l\}\). If \(N_l(S) = T\), then we cannot increase the size of the alternating path (and therefore can't further augment), so we need to improve the labeling. Let \(\delta_l\) be the minimum of \(l(u) + l(v) - w(u,v)\) over all of the \(u \in S\) and \(v \notin T\). Improve the labeling \(l\) to \(l'\): If \(r \in S,\) then \(l'(r) = l(r) - \delta_l,\) If \(r \in T,\) then \(l'(r) = l(r) + \delta_l.\) If \(r \notin S\) and \(r \notin T,\) then \(l'(r) = l(r).\) \(l'\) is a valid labeling and \(E_l \subset E_{l'}.\) Putting it all together: The Hungarian Algorithm Start with some matching \(M\), a valid labeling \(l\), where \(l\) is defined as the labelling \(\forall x \in X, y \in Y| l(y) = 0, l(x) = \text{ max}_{y \in Y}(w\big(x, y)\big)\). Do these steps until a perfect matching is found \((\)when \(M\) is perfect\():\) (a) Look for an augmenting path in \(M.\) (b) If an augmenting path does not exist, improve the labeling and then go back to step (a).

Each step will increase the size of the matching \(M\) or it will increase the size of the set of labeled edges, \(E_l\). This means that the process will eventually terminate since there are only so many edges in the graph \(G\). [4]

When the process terminates, \(M\) will be a perfect matching. By the Kuhn-Munkres theorem , this means that the matching is a maximum-weight matching.

The algorithm defined above can be implemented in the soccer scenario. First, the conflicting node is identified, implying that there is an alternating tree that must be reconfigured.

There is an alternating path between defense, Eva, mid, and Tom.

To find the best appropriate node, find the minimum \(\delta_l\), as defined in step 4 above, where \(l_u\) is the label for player \(u,\) \(l_v\) is the label for position \(v,\) and \(w_{u, v}\) is the weight on that edge.

The \(\delta_l\) of each unmatched node is computed, where the minimum is found to be a value of 2, between Tom playing mid \((8 + 0 – 6 = 2).\)

The labels are then augmented and the new edges are graphed in the example. Notice that defense and mid went down by 2 points, whereas Eva’s skillset got back two points. However, this is expected as Eva can't play in both positions at once.

Augmenting path leads to relabeling of nodes, which gives rise to the maximum-weighted path.

These new edges complete the perfect matching of the graph, which implies that a maximum-weighted graph has been found and the algorithm can terminate.

The complexity of the algorithm will be analyzed using the graph-based technique as a reference, yet the result is the same as for the matrix-based one.

Algorithm analysis [3] At each \(a\) or \(b\) step, the algorithm adds one edge to the matching and this happens \(O\big(|V|\big)\) times. It takes \(O\big(|V|\big)\) time to find the right vertex for the augmenting (if there is one at all), and it is \(O\big(|V|\big)\) time to flip the matching. Improving the labeling takes \(O\big(|V|\big)\) time to find \(\delta_l\) and to update the labelling accordingly. We might have to improve the labeling up to \(O\big(|V|\big)\) times if there is no augmenting path. This makes for a total of \(O\big(|V|^2\big)\) time. In all, there are \(O\big(|V|\big)\) iterations each taking \(O\big(|V|\big)\) work, leading to a total running time of \(O\big(|V|^3\big)\).

• Matching Algorithms
• Bruff, D. The Assignment Problem and the Hungarian Method . Retrieved June 26, 2016, from http://www.math.harvard.edu/archive/20_spring_05/handouts/assignment_overheads.pdf
• Golin, M. Bipartite Matching & the Hungarian Method . Retrieved Retrieved June 26th, 2016, from http://www.cse.ust.hk/~golin/COMP572/Notes/Matching.pdf
• Grinman, A. The Hungarian Algorithm for Weighted Bipartite Graphs . Retrieved June 26, 2016, from http://math.mit.edu/~rpeng/18434/hungarianAlgorithm.pdf
• Golin, M. Bipartite Matching & the Hungarian Method . Retrieved June 26, 2016, from http://www.cse.ust.hk/~golin/COMP572/Notes/Matching.pdf

Problem Loading...

Note Loading...

Set Loading...

Hungarian Method

The Hungarian method is a computational optimization technique that addresses the assignment problem in polynomial time and foreshadows following primal-dual alternatives. In 1955, Harold Kuhn used the term “Hungarian method” to honour two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry. Let’s go through the steps of the Hungarian method with the help of a solved example.

Hungarian Method to Solve Assignment Problems

The Hungarian method is a simple way to solve assignment problems. Let us first discuss the assignment problems before moving on to learning the Hungarian method.

What is an Assignment Problem?

A transportation problem is a type of assignment problem. The goal is to allocate an equal amount of resources to the same number of activities. As a result, the overall cost of allocation is minimised or the total profit is maximised.

Because available resources such as workers, machines, and other resources have varying degrees of efficiency for executing different activities, and hence the cost, profit, or loss of conducting such activities varies.

Assume we have ‘n’ jobs to do on ‘m’ machines (i.e., one job to one machine). Our goal is to assign jobs to machines for the least amount of money possible (or maximum profit). Based on the notion that each machine can accomplish each task, but at variable levels of efficiency.

Hungarian Method Steps

Check to see if the number of rows and columns are equal; if they are, the assignment problem is considered to be balanced. Then go to step 1. If it is not balanced, it should be balanced before the algorithm is applied.

Step 1 – In the given cost matrix, subtract the least cost element of each row from all the entries in that row. Make sure that each row has at least one zero.

Step 2 – In the resultant cost matrix produced in step 1, subtract the least cost element in each column from all the components in that column, ensuring that each column contains at least one zero.

Step 3 – Assign zeros

• Analyse the rows one by one until you find a row with precisely one unmarked zero. Encircle this lonely unmarked zero and assign it a task. All other zeros in the column of this circular zero should be crossed out because they will not be used in any future assignments. Continue in this manner until you’ve gone through all of the rows.
• Examine the columns one by one until you find one with precisely one unmarked zero. Encircle this single unmarked zero and cross any other zero in its row to make an assignment to it. Continue until you’ve gone through all of the columns.

Step 4 – Perform the Optimal Test

• The present assignment is optimal if each row and column has exactly one encircled zero.
• The present assignment is not optimal if at least one row or column is missing an assignment (i.e., if at least one row or column is missing one encircled zero). Continue to step 5. Subtract the least cost element from all the entries in each column of the final cost matrix created in step 1 and ensure that each column has at least one zero.

Step 5 – Draw the least number of straight lines to cover all of the zeros as follows:

(a) Highlight the rows that aren’t assigned.

(b) Label the columns with zeros in marked rows (if they haven’t already been marked).

(c) Highlight the rows that have assignments in indicated columns (if they haven’t previously been marked).

(d) Continue with (b) and (c) until no further marking is needed.

(f) Simply draw the lines through all rows and columns that are not marked. If the number of these lines equals the order of the matrix, then the solution is optimal; otherwise, it is not.

Step 6 – Find the lowest cost factor that is not covered by the straight lines. Subtract this least-cost component from all the uncovered elements and add it to all the elements that are at the intersection of these straight lines, but leave the rest of the elements alone.

Step 7 – Continue with steps 1 – 6 until you’ve found the highest suitable assignment.

Hungarian Method Example

Use the Hungarian method to solve the given assignment problem stated in the table. The entries in the matrix represent each man’s processing time in hours.

\(\begin{array}{l}\begin{bmatrix} & I & II & III & IV & V \\1 & 20 & 15 & 18 & 20 & 25 \\2 & 18 & 20 & 12 & 14 & 15 \\3 & 21 & 23 & 25 & 27 & 25 \\4 & 17 & 18 & 21 & 23 & 20 \\5 & 18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} \)

With 5 jobs and 5 men, the stated problem is balanced.

\(\begin{array}{l}A = \begin{bmatrix}20 & 15 & 18 & 20 & 25 \\18 & 20 & 12 & 14 & 15 \\21 & 23 & 25 & 27 & 25 \\17 & 18 & 21 & 23 & 20 \\18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} \)

Subtract the lowest cost element in each row from all of the elements in the given cost matrix’s row. Make sure that each row has at least one zero.

\(\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 5 & 10 \\6 & 8 & 0 & 2 & 3 \\0 & 2 & 4 & 6 & 4 \\0 & 1 & 4 & 6 & 3 \\2 & 2 & 0 & 3 & 4 \\\end{bmatrix}\end{array} \)

Subtract the least cost element in each Column from all of the components in the given cost matrix’s Column. Check to see if each column has at least one zero.

\(\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 3 & 7 \\6 & 8 & 0 & 0 & 0 \\0 & 2 & 4 & 4 & 1 \\0 & 1 & 4 & 4 & 0 \\2 & 2 & 0 & 1 & 1 \\\end{bmatrix}\end{array} \)

When the zeros are assigned, we get the following:

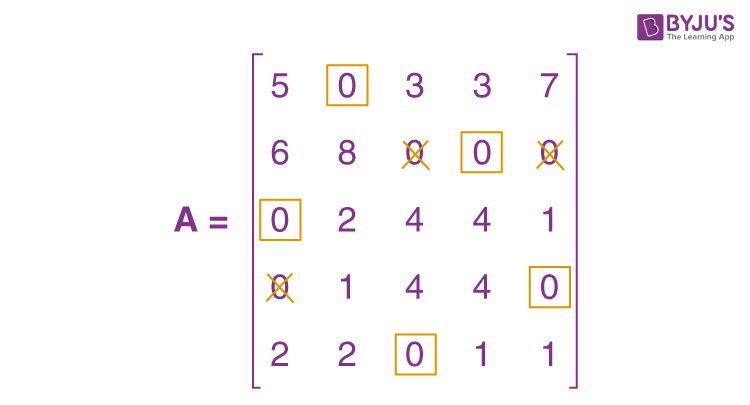
The present assignment is optimal because each row and column contain precisely one encircled zero.

Where 1 to II, 2 to IV, 3 to I, 4 to V, and 5 to III are the best assignments.

Hence, z = 15 + 14 + 21 + 20 + 16 = 86 hours is the optimal time.

Practice Question on Hungarian Method

Use the Hungarian method to solve the following assignment problem shown in table. The matrix entries represent the time it takes for each job to be processed by each machine in hours.

\(\begin{array}{l}\begin{bmatrix}J/M & I & II & III & IV & V \\1 & 9 & 22 & 58 & 11 & 19 \\2 & 43 & 78 & 72 & 50 & 63 \\3 & 41 & 28 & 91 & 37 & 45 \\4 & 74 & 42 & 27 & 49 & 39 \\5 & 36 & 11 & 57 & 22 & 25 \\\end{bmatrix}\end{array} \)

Stay tuned to BYJU’S – The Learning App and download the app to explore all Maths-related topics.

Frequently Asked Questions on Hungarian Method

What is hungarian method.

The Hungarian method is defined as a combinatorial optimization technique that solves the assignment problems in polynomial time and foreshadowed subsequent primal–dual approaches.

What are the steps involved in Hungarian method?

The following is a quick overview of the Hungarian method: Step 1: Subtract the row minima. Step 2: Subtract the column minimums. Step 3: Use a limited number of lines to cover all zeros. Step 4: Add some more zeros to the equation.

What is the purpose of the Hungarian method?

When workers are assigned to certain activities based on cost, the Hungarian method is beneficial for identifying minimum costs.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Assignment Problem: Meaning, Methods and Variations | Operations Research

After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations.

Meaning of Assignment Problem:

An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total cost or maximize total profit of allocation.

The problem of assignment arises because available resources such as men, machines etc. have varying degrees of efficiency for performing different activities, therefore, cost, profit or loss of performing the different activities is different.

Thus, the problem is “How should the assignments be made so as to optimize the given objective”. Some of the problem where the assignment technique may be useful are assignment of workers to machines, salesman to different sales areas.

Definition of Assignment Problem:

ADVERTISEMENTS:

Suppose there are n jobs to be performed and n persons are available for doing these jobs. Assume that each person can do each job at a term, though with varying degree of efficiency, let c ij be the cost if the i-th person is assigned to the j-th job. The problem is to find an assignment (which job should be assigned to which person one on-one basis) So that the total cost of performing all jobs is minimum, problem of this kind are known as assignment problem.

The assignment problem can be stated in the form of n x n cost matrix C real members as given in the following table:

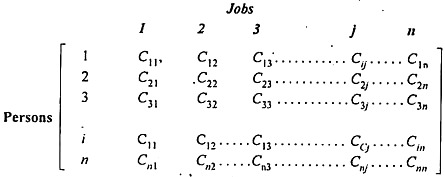
• Google OR-Tools
• Español – América Latina
• Português – Brasil
• Tiếng Việt

Solving an Assignment Problem

This section presents an example that shows how to solve an assignment problem using both the MIP solver and the CP-SAT solver.

In the example there are five workers (numbered 0-4) and four tasks (numbered 0-3). Note that there is one more worker than in the example in the Overview .

The costs of assigning workers to tasks are shown in the following table.

The problem is to assign each worker to at most one task, with no two workers performing the same task, while minimizing the total cost. Since there are more workers than tasks, one worker will not be assigned a task.

MIP solution

The following sections describe how to solve the problem using the MPSolver wrapper .

Import the libraries

The following code imports the required libraries.

Create the data

The following code creates the data for the problem.

The costs array corresponds to the table of costs for assigning workers to tasks, shown above.

Declare the MIP solver

The following code declares the MIP solver.

Create the variables

The following code creates binary integer variables for the problem.

Create the constraints

Create the objective function.

The following code creates the objective function for the problem.

The value of the objective function is the total cost over all variables that are assigned the value 1 by the solver.

Invoke the solver

The following code invokes the solver.

Print the solution

The following code prints the solution to the problem.

Here is the output of the program.

Complete programs

Here are the complete programs for the MIP solution.

CP SAT solution

The following sections describe how to solve the problem using the CP-SAT solver.

Declare the model

The following code declares the CP-SAT model.

The following code sets up the data for the problem.

The following code creates the constraints for the problem.

Here are the complete programs for the CP-SAT solution.

Except as otherwise noted, the content of this page is licensed under the Creative Commons Attribution 4.0 License , and code samples are licensed under the Apache 2.0 License . For details, see the Google Developers Site Policies . Java is a registered trademark of Oracle and/or its affiliates.

Last updated 2023-01-02 UTC.

Index     Assignment problem     Hungarian algorithm     Solve online    

Solve an assignment problem online

Fill in the cost matrix of an assignment problem and click on 'Solve'. The optimal assignment will be determined and a step by step explanation of the hungarian algorithm will be given.

Fill in the cost matrix ( random cost matrix ):

Don't show the steps of the Hungarian algorithm Maximize the total cost

HungarianAlgorithm.com © 2013-2024

How to Solve the Assignment Problem: A Complete Guide

Table of Contents

Assignment problem is a special type of linear programming problem that deals with assigning a number of resources to an equal number of tasks in the most efficient way. The goal is to minimize the total cost of assignments while ensuring that each task is assigned to only one resource and each resource is assigned to only one task. In this blog, we will discuss the solution of the assignment problem using the Hungarian method, which is a popular algorithm for solving the problem.

Understanding the Assignment Problem

Before we dive into the solution, it is important to understand the problem itself. In the assignment problem, we have a matrix of costs, where each row represents a resource and each column represents a task. The objective is to assign each resource to a task in such a way that the total cost of assignments is minimized. However, there are certain constraints that need to be satisfied – each resource can be assigned to only one task and each task can be assigned to only one resource.

Solving the Assignment Problem

There are various methods for solving the assignment problem, including the Hungarian method, the brute force method, and the auction algorithm. Here, we will focus on the steps involved in solving the assignment problem using the Hungarian method, which is the most commonly used and efficient method.

Step 1: Set up the cost matrix

The first step in solving the assignment problem is to set up the cost matrix, which represents the cost of assigning a task to an agent. The matrix should be square and have the same number of rows and columns as the number of tasks and agents, respectively.

Step 2: Subtract the smallest element from each row and column

To simplify the calculations, we need to reduce the size of the cost matrix by subtracting the smallest element from each row and column. This step is called matrix reduction.

Step 3: Cover all zeros with the minimum number of lines

The next step is to cover all zeros in the matrix with the minimum number of horizontal and vertical lines. This step is called matrix covering.

Step 4: Test for optimality and adjust the matrix

To test for optimality, we need to calculate the minimum number of lines required to cover all zeros in the matrix. If the number of lines equals the number of rows or columns, the solution is optimal. If not, we need to adjust the matrix and repeat steps 3 and 4 until we get an optimal solution.

Step 5: Assign the tasks to the agents

The final step is to assign the tasks to the agents based on the optimal solution obtained in step 4. This will give us the most cost-effective or profit-maximizing assignment.

Solution of the Assignment Problem using the Hungarian Method

The Hungarian method is an algorithm that uses a step-by-step approach to find the optimal assignment. The algorithm consists of the following steps:

• Subtract the smallest entry in each row from all the entries of the row.
• Subtract the smallest entry in each column from all the entries of the column.
• Draw the minimum number of lines to cover all zeros in the matrix. If the number of lines drawn is equal to the number of rows, we have an optimal solution. If not, go to step 4.
• Determine the smallest entry not covered by any line. Subtract it from all uncovered entries and add it to all entries covered by two lines. Go to step 3.

The above steps are repeated until an optimal solution is obtained. The optimal solution will have all zeros covered by the minimum number of lines. The assignments can be made by selecting the rows and columns with a single zero in the final matrix.

Applications of the Assignment Problem

The assignment problem has various applications in different fields, including computer science, economics, logistics, and management. In this section, we will provide some examples of how the assignment problem is used in real-life situations.

Applications in Computer Science

The assignment problem can be used in computer science to allocate resources to different tasks, such as allocating memory to processes or assigning threads to processors.

Applications in Economics

The assignment problem can be used in economics to allocate resources to different agents, such as allocating workers to jobs or assigning projects to contractors.

Applications in Logistics

The assignment problem can be used in logistics to allocate resources to different activities, such as allocating vehicles to routes or assigning warehouses to customers.

Applications in Management

The assignment problem can be used in management to allocate resources to different projects, such as allocating employees to tasks or assigning budgets to departments.

Let’s consider the following scenario: a manager needs to assign three employees to three different tasks. Each employee has different skills, and each task requires specific skills. The manager wants to minimize the total time it takes to complete all the tasks. The skills and the time required for each task are given in the table below:

The assignment problem is to determine which employee should be assigned to which task to minimize the total time required. To solve this problem, we can use the Hungarian method, which we discussed in the previous blog.

Using the Hungarian method, we first subtract the smallest entry in each row from all the entries of the row:

Next, we subtract the smallest entry in each column from all the entries of the column:

We draw the minimum number of lines to cover all the zeros in the matrix, which in this case is three:

Since the number of lines is equal to the number of rows, we have an optimal solution. The assignments can be made by selecting the rows and columns with a single zero in the final matrix. In this case, the optimal assignments are:

• Emp 1 to Task 3
• Emp 2 to Task 2
• Emp 3 to Task 1

This assignment results in a total time of 9 units.

I hope this example helps you better understand the assignment problem and how to solve it using the Hungarian method.

Solving the assignment problem may seem daunting, but with the right approach, it can be a straightforward process. By following the steps outlined in this guide, you can confidently tackle any assignment problem that comes your way.

How useful was this post?

Click on a star to rate it!

Average rating 0 / 5. Vote count: 0

No votes so far! Be the first to rate this post.

We are sorry that this post was not useful for you! 😔

Let us improve this post!

Tell us how we can improve this post?

Operations Research

1 Operations Research-An Overview

• History of O.R.
• Approach, Techniques and Tools
• Phases and Processes of O.R. Study
• Typical Applications of O.R
• Limitations of Operations Research
• Models in Operations Research
• O.R. in real world

2 Linear Programming: Formulation and Graphical Method

• General formulation of Linear Programming Problem
• Optimisation Models
• Basics of Graphic Method
• Important steps to draw graph
• Multiple, Unbounded Solution and Infeasible Problems
• Solving Linear Programming Graphically Using Computer
• Application of Linear Programming in Business and Industry

3 Linear Programming-Simplex Method

• Principle of Simplex Method
• Computational aspect of Simplex Method
• Simplex Method with several Decision Variables
• Two Phase and M-method
• Multiple Solution, Unbounded Solution and Infeasible Problem
• Sensitivity Analysis
• Dual Linear Programming Problem

4 Transportation Problem

• Basic Feasible Solution of a Transportation Problem
• Modified Distribution Method
• Stepping Stone Method
• Unbalanced Transportation Problem
• Degenerate Transportation Problem
• Transhipment Problem
• Maximisation in a Transportation Problem

5 Assignment Problem

• Solution of the Assignment Problem
• Unbalanced Assignment Problem
• Problem with some Infeasible Assignments
• Maximisation in an Assignment Problem
• Crew Assignment Problem

6 Application of Excel Solver to Solve LPP

• Building Excel model for solving LP: An Illustrative Example

7 Goal Programming

• Concepts of goal programming
• Goal programming model formulation
• Graphical method of goal programming
• The simplex method of goal programming
• Using Excel Solver to Solve Goal Programming Models
• Application areas of goal programming

8 Integer Programming

• Some Integer Programming Formulation Techniques
• Binary Representation of General Integer Variables
• Unimodularity
• Cutting Plane Method
• Branch and Bound Method
• Solver Solution

9 Dynamic Programming

• Dynamic Programming Methodology: An Example
• Definitions and Notations
• Dynamic Programming Applications

10 Non-Linear Programming

• Solution of a Non-linear Programming Problem
• Convex and Concave Functions
• Kuhn-Tucker Conditions for Constrained Optimisation
• Quadratic Programming
• Separable Programming
• NLP Models with Solver

11 Introduction to game theory and its Applications

• Important terms in Game Theory
• Saddle points
• Mixed strategies: Games without saddle points
• 2 x n games
• Exploiting an opponent’s mistakes

12 Monte Carlo Simulation

• Reasons for using simulation
• Monte Carlo simulation
• Limitations of simulation
• Steps in the simulation process
• Some practical applications of simulation
• Two typical examples of hand-computed simulation
• Computer simulation

13 Queueing Models

• Characteristics of a queueing model
• Notations and Symbols
• Statistical methods in queueing
• The M/M/I System
• The M/M/C System
• The M/Ek/I System
• Decision problems in queueing

The assignment problem revisited

• Original Paper
• Published: 16 August 2021
• Volume 16 , pages 1531–1548, ( 2022 )

Cite this article

• Carlos A. Alfaro   ORCID: orcid.org/0000-0001-9783-8587 1 ,
• Sergio L. Perez 2 ,
• Carlos E. Valencia 3 &
• Marcos C. Vargas 1  

1013 Accesses

4 Citations

4 Altmetric

Explore all metrics

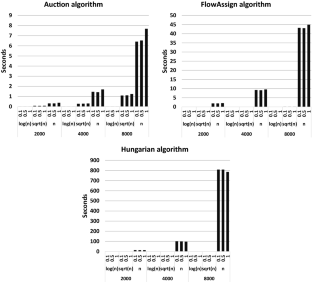
First, we give a detailed review of two algorithms that solve the minimization case of the assignment problem, the Bertsekas auction algorithm and the Goldberg & Kennedy algorithm. It was previously alluded that both algorithms are equivalent. We give a detailed proof that these algorithms are equivalent. Also, we perform experimental results comparing the performance of three algorithms for the assignment problem: the \(\epsilon \) - scaling auction algorithm , the Hungarian algorithm and the FlowAssign algorithm . The experiment shows that the auction algorithm still performs and scales better in practice than the other algorithms which are harder to implement and have better theoretical time complexity.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Similar content being viewed by others

Bias-constrained integer least squares estimation: distributional properties and applications in GNSS ambiguity resolution

Learning to optimize: A tutorial for continuous and mixed-integer optimization

Information complexity of mixed-integer convex optimization

Bertsekas, D.P.: The auction algorithm: a distributed relaxation method for the assignment problem. Annal Op. Res. 14 , 105–123 (1988)

Article   MathSciNet   Google Scholar  

Bertsekas, D.P., Castañon, D.A.: Parallel synchronous and asynchronous implementations of the auction algorithm. Parallel Comput. 17 , 707–732 (1991)

Article   Google Scholar  

Bertsekas, D.P.: Linear network optimization: algorithms and codes. MIT Press, Cambridge, MA (1991)

MATH   Google Scholar  

Bertsekas, D.P.: The auction algorithm for shortest paths. SIAM J. Optim. 1 , 425–477 (1991)

Bertsekas, D.P.: Auction algorithms for network flow problems: a tutorial introduction. Comput. Optim. Appl. 1 , 7–66 (1992)

Bertsekas, D.P., Castañon, D.A., Tsaknakis, H.: Reverse auction and the solution of inequality constrained assignment problems. SIAM J. Optim. 3 , 268–299 (1993)

Bertsekas, D.P., Eckstein, J.: Dual coordinate step methods for linear network flow problems. Math. Progr., Ser. B 42 , 203–243 (1988)

Bertsimas, D., Tsitsiklis, J.N.: Introduction to linear optimization. Athena Scientific, Belmont, MA (1997)

Google Scholar  

Burkard, R., Dell’Amico, M., Martello, S.: Assignment Problems. Revised reprint. SIAM, Philadelphia, PA (2011)

Gabow, H.N., Tarjan, R.E.: Faster scaling algorithms for network problems. SIAM J. Comput. 18 (5), 1013–1036 (1989)

Goldberg, A.V., Tarjan, R.E.: A new approach to the maximum flow problem. J. Assoc. Comput. Mach. 35 , 921–940 (1988)

Goldberg, A.V., Tarjan, R.E.: Finding minimum-cost circulations by successive approximation. Math. Op. Res. 15 , 430–466 (1990)

Goldberg, A.V., Kennedy, R.: An efficient cost scaling algorithm for the assignment problem. Math. Programm. 71 , 153–177 (1995)

MathSciNet   MATH   Google Scholar  

Goldberg, A.V., Kennedy, R.: Global price updates help. SIAM J. Discr. Math. 10 (4), 551–572 (1997)

Kuhn, H.W.: The Hungarian method for the assignment problem. Naval Res. Logist. Quart. 2 , 83–97 (1955)

Kuhn, H.W.: Variants of the Hungarian method for the assignment problem. Naval Res. Logist. Quart. 2 , 253–258 (1956)

Lawler, E.L.: Combinatorial optimization: networks and matroids, Holt. Rinehart & Winston, New York (1976)

Orlin, J.B., Ahuja, R.K.: New scaling algorithms for the assignment ad minimum mean cycle problems. Math. Programm. 54 , 41–56 (1992)

Ramshaw, L., Tarjan, R.E., Weight-Scaling Algorithm, A., for Min-Cost Imperfect Matchings in Bipartite Graphs, : IEEE 53rd Annual Symposium on Foundations of Computer Science. New Brunswick, NJ 2012 , 581–590 (2012)

Zaki, H.: A comparison of two algorithms for the assignment problem. Comput. Optim. Appl. 4 , 23–45 (1995)

Download references

Acknowledgements

This research was partially supported by SNI and CONACyT.

Author information

Authors and affiliations.

Banco de México, Mexico City, Mexico

Carlos A. Alfaro & Marcos C. Vargas

Mountain View, CA, 94043, USA

Sergio L. Perez

Departamento de Matemáticas, CINVESTAV del IPN, Apartado postal 14-740, 07000, Mexico City, Mexico

Carlos E. Valencia

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Carlos A. Alfaro .

Ethics declarations

Conflict of interest.

There is no conflict of interest.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The authors were partially supported by SNI and CONACyT.

Rights and permissions

Reprints and permissions

About this article

Alfaro, C.A., Perez, S.L., Valencia, C.E. et al. The assignment problem revisited. Optim Lett 16 , 1531–1548 (2022). https://doi.org/10.1007/s11590-021-01791-4

Download citation

Received : 26 March 2020

Accepted : 03 August 2021

Published : 16 August 2021

Issue Date : June 2022

DOI : https://doi.org/10.1007/s11590-021-01791-4

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Assignment problem
• Bertsekas auction algorithm
• Combinatorial optimization and matching
• Find a journal
• Publish with us
• Track your research

Hungarian Algorithm Introduction & Python Implementation

How to use hungarian method to resolve the linear assignment problem..

By Eason on 2021-08-02

In this article, I will introduce how to use Hungarian Method to resolve the linear assignment problem and provide my personal Python code solution.

So… What is the linear assignment problem?

The linear assignment problem represents the need to maximize the available resources (or minimize the expenditure) with limited resources. For instance, below is a 2D matrix, where each row represents a different supplier, and each column represents the cost of employing them to produce a particular product. Each supplier can only specialize in the production of one of these products. In other words, only one element can be selected for each column and row in the matrix, and the sum of the selected elements must be minimized (minimized cost expense).

The cost of producing different goods by different producers:

Indeed, this is a simple example. By trying out the possible combinations, we can see that the smallest sum is 13, so supplier A supplies Bubble Tea , supplier B supplies milk tea, and supplier C supplies Fruit Tea . However, such attempts do not follow a clear rule and become inefficient when applied to large tasks. Therefore, the next section will introduce step by step the Hungarian algorithm, which can be applied to the linear assignment problem.

Hungarian Algorithm & Python Code Step by Step

In this section, we will show how to use the Hungarian algorithm to solve linear assignment problems and find the minimum combinations in the matrix. Of course, the Hungarian algorithm can also be used to find the maximum combination.

Step 0. Prepare Operations

First, an N by N matrix is generated to be used for the Hungarian algorithm (Here, we use a 5 by 5 square matrix as an example).

The above code randomly generates a 5x5 cost matrix of integers between 0 and 10.

If we want to find the maximum sum, we could do the opposite. The matrix to be solved is regarded as the profit matrix, and the maximum value in the matrix is set as the common price of all goods. The cost matrix is obtained by subtracting the profit matrix from the maximum value. Finally, the cost matrix is substituted into the Hungarian algorithm to obtain the minimized combination and then remapped back to the profit matrix to obtain the maximized sum value and composition result.

The above code randomly generates a 5x5 profit matrix of integers between 0 and 10 and generate a corresponding cost matrix

By following the steps above, you can randomly generate either the cost matrix or the profit matrix. Next, we will move into the introduction of the Hungarian algorithm, and for the sake of illustration, the following sections will be illustrated using the cost matrix shown below. We will use the Hungarian algorithm to solve the linear assignment problem of the cost matrix and find the corresponding minimum sum.

Example cost matrix:

Step 1. Every column and every row subtract its internal minimum

First, every column and every row must subtract its internal minimum. After subtracting the minimum, the cost matrix will look like this.

Cost matrix after step 1:

And the current code is like this:

Step 2.1. Min_zero_row Function Implementation

At first, we need to find the row with the fewest zero elements. So, we can convert the previous matrix to the boolean matrix(0 → True, Others → False).

Transform matrix to boolean matrix:

Corresponding Boolean matrix:

Therefore, we can use the “min_zero_row” function to find the corresponding row.

The row which contains the least 0:

Third, mark any 0 elements on the corresponding row and clean up its row and column (converts elements on the Boolean matrix to False). The coordinates of the element are stored in mark_zero.

Hence, the boolean matrix will look like this:

The boolean matrix after the first process. The fourth row has been changed to all False.

The process is repeated several times until the elements in the boolean matrix are all False. The below picture shows the order in which they are marked.

The possible answer composition:

Step 2.2. Mark_matrix Function Implementation

After getting Zero_mat from the step 2–1, we can check it and mark the matrix according to certain rules. The whole rule can be broken down into several steps:

• Mark rows that do not contain marked 0 elements and store row indexes in the non_marked_row
• Search non_marked_row element, and find out if there are any unmarked 0 elements in the corresponding column
• Store the column indexes in the marked_cols
• Compare the column indexes stored in marked_zero and marked_cols
• If a matching column index exists, the corresponding row_index is saved to non_marked_rows
• Next, the row indexes that are not in non_marked_row are stored in marked_rows

Finally, the whole mark_matrx function is finished and then returns marked_zero , marked_rows , marked_cols. At this point, we will be able to decide the result based on the return information.

If we use the example cost matrix, the corresponding marked_zero , marked_rows, and marked_cols are as follows:

• marked_zero : [(3, 2), (0, 4), (1, 1), (2, 0), (4, 3)]
• marked_rows : [0, 1, 2, 3, 4]
• marked_cols : []

Step 3. Identify the Result

At this step, if the sum of the lengths of marked_rows and marked_cols is equal to the length of the cost matrix, it means that the solution of the linear assignment problem has been found successfully, and marked_zero stores the solution coordinates. Fortunately, in the example matrix, we find the answer on the first try. Therefore, we can skip to step 5 and calculate the solution.

However, everything is hardly plain sailing. Most of the time, we will not find the solution on the first try, such as the following matrix:

After Step 1 & 2 , the corresponding matrix, marked_rows, and marked_cols are as follows:

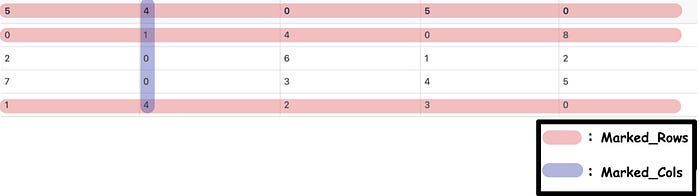
The sum of the lengths of Marked_Rows and Marked_Cols is 4 (less than 5).

Apparently, the sum of the lengths is less than the length of the matrix. At this time, we need to go into Step 4 to adjust the matrix.

Step 4. Adjust Matrix

In Step 4, we're going to put the matrix after Step 1 into the Adjust_Matrix function . Taking the latter matrix in Step 3 as an example, the matrix to be modified in Adjust_Matrix is:

The whole function can be separated into three steps:

• Find the minimum value for an element that is not in marked_rows and not in marked_cols . Hence, we can find the minimum value is 1.

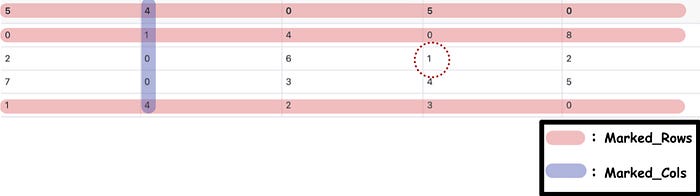
• Subtract the elements which not in marked_rows nor marked_cols from the minimum values obtained in the previous step.

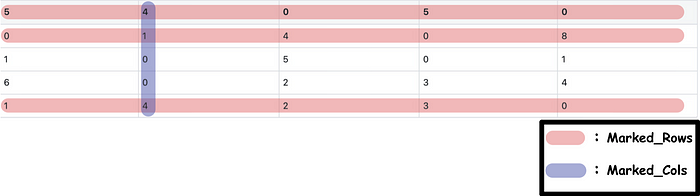
• Add the element in marked_rows , which is also in marked_cols , to the minimum value obtained by Step 4–1.

Return the adjusted matrix and repeat Step 2 and Step 3 until the conditions satisfy the requirement of entering Step 5.

Step 5. Calculate the Answer

Using the element composition stored in marked_zero , the minimum and maximum values of the linear assignment problem can be calculated.

The minimum composition of the assigned matrix and the minimum sum is 18.

The maximum composition of the assigned matrix and the maximum sum is 43.

The code of the Answer_Calculator function is as follows:

The complete code is as follows:

Hungarian algorithm - Wikipedia

Continue Learning

How to find all possible combinations in a list (and their sum) with python.

Mini-learns with Python 3

From API to Pandas—Getting JSON Data With Python

A working example of getting JSON data from an API to a Pandas DataFrame in Python with Google Colab and Open Data DC.

How to Create a Web Map with Leaflet and Python

How to upgrade python to 3.10.

Python 3.10 Has been Released (October 4, 2021)! Give it a try!

How to Scrape Everything From Instagram Using Python

A guide on scraping from Instagram using Python.

A Python Example of the Flood Fill Algorithm

A brief tutorial on the Flood Fill algorithm

Excel Tutorial: How To Solve Assignment Problem In Excel

Introduction.

Have you ever faced the challenge of assigning a set of tasks to a group of resources in Excel? This is what we call the assignment problem in Excel. It is a common issue faced by many professionals, and finding an efficient solution can greatly improve productivity and resource utilization. In this tutorial, we will guide you through the process of solving the assignment problem in Excel, and explain why it is important to master this skill.

Key Takeaways

• Solving the assignment problem in Excel can greatly improve productivity and resource utilization.
• Understanding the assignment problem and its real-life applications is important for professionals.
• Organizing and managing data accurately is crucial for solving the assignment problem in Excel.
• Using the Solver tool effectively can help find optimal solutions for the assignment problem.
• Efficiency tips and avoiding common mistakes can streamline the problem-solving process in Excel.

Understanding the Assignment Problem

The assignment problem is a fundamental optimization problem that involves finding the most efficient assignment of tasks to resources. In other words, it is the process of finding the best possible way to allocate a set of resources to a set of tasks in such a way that the overall cost or time is minimized.

The assignment problem can be defined as a special case of the transportation problem, where the objective is to minimize the cost of assigning a set of tasks to a set of resources, given certain constraints and limitations.

There are different types of assignment problems, including the balanced assignment problem, unbalanced assignment problem, and the generalized assignment problem. The balanced assignment problem occurs when the number of resources is equal to the number of tasks, while the unbalanced assignment problem occurs when the number of resources is not equal to the number of tasks. The generalized assignment problem allows for assigning a task to multiple resources, but with different costs associated with each assignment.

The assignment problem has numerous real-life applications, such as in workforce scheduling, project management, and supply chain optimization. In Excel, the assignment problem can be solved using various optimization techniques and algorithms, such as the Hungarian method, the auction algorithm, and the shortest path algorithm. These techniques can be implemented using Excel's built-in solver tool, which allows users to find the optimal solution to assignment problems by minimizing a given objective function, subject to certain constraints.

Setting up the Data in Excel

When it comes to solving the assignment problem in Excel, setting up the data properly is crucial for accurate and efficient analysis. In this chapter, we will discuss how to organize the data, use Excel tables for better data management, and ensure data accuracy and completeness.

• Identify the assignment problem variables and constraints
• Create a separate section in Excel for each variable and constraint
• Ensure the data is organized in a clear and logical manner for easy analysis
• Create an Excel table for each section of the assignment problem
• Use table features such as filtering and sorting to easily manipulate and analyze the data
• Utilize the structured format of tables for improved data organization and readability
• Double-check all data entries for accuracy
• Verify that all variables and constraints are accounted for in the data
• Use validation and error-checking features in Excel to minimize data errors

Using Solver Tool in Excel

Excel’s Solver tool is a powerful feature that allows users to find the optimal solution to complex problems, such as the assignment problem. By utilizing the Solver tool, you can efficiently allocate resources and optimize various aspects of your business or project.

Accessing the Solver tool in Excel

To access the Solver tool in Excel, you first need to ensure that it is installed as an add-in. You can do this by navigating to the “File” tab, selecting “Options,” and then clicking on “Add-Ins.” From there, you can enable the Solver add-in, which will then appear in the “Data” tab under the “Analysis” group.

Defining the objective and constraints

Once the Solver tool is accessible, you can begin defining the objective and constraints of your assignment problem. The objective is the goal you want to achieve, such as maximizing profits or minimizing costs. Constraints are the limitations or restrictions that must be considered, such as resource availability or capacity.

Running the Solver to find the optimal solution

After defining the objective and constraints, you can then run the Solver to find the optimal solution to your assignment problem. The Solver tool will utilize algorithms to analyze various combinations and iterations to determine the best possible outcome based on the defined parameters.

Interpreting the Results

After using Excel to solve the assignment problem, it is important to understand and interpret the results to ensure accuracy and make any necessary adjustments.

• Objective Function: The Solver provides the optimal value of the objective function, which represents the minimum cost or maximum profit.
• Variable Values: It also provides the optimal values for the decision variables, indicating the allocation of resources to tasks.
• Check Constraints: Ensure that all constraints are satisfied by the solution, such as resource limits and task requirements.
• Sensitivity Analysis: Conduct sensitivity analysis to understand how changes in inputs or constraints affect the solution.
• Scenario Analysis: Explore different scenarios by adjusting input values or constraints to evaluate alternative solutions.
• Iterative Process: If the initial solution is not optimal, iterate by making adjustments and re-solving the problem using Solver.

Tips for Efficiency

Efficiency is key when solving assignment problems in Excel. By utilizing shortcuts, functions, and avoiding common mistakes, you can streamline the process and save valuable time.

• Keyboard shortcuts: Familiarize yourself with common keyboard shortcuts in Excel to quickly perform functions such as copying, pasting, and formatting.
• Use of built-in functions: Take advantage of Excel's built-in functions such as VLOOKUP, INDEX, and MATCH to streamline the assignment problem-solving process.
• Organize data: Before starting to solve the assignment problem, ensure that your data is properly organized and formatted to avoid confusion and errors.
• Utilize templates: Consider creating templates or using pre-existing ones to simplify the process and avoid starting from scratch each time.
• Double-check formulas: Always double-check your formulas to avoid errors that can lead to incorrect solutions.
• Use of absolute references: When working with formulas, use absolute references to ensure that cell references do not change unintentionally.

Recap: Solving assignment problems in Excel is crucial for efficient project management and decision-making. It allows for optimal allocation of resources and time, leading to streamlined workflows and increased productivity.

Encouragement: Practice makes perfect, and the same goes for mastering Excel. I encourage you to continue practicing and applying the tutorial steps to become proficient in solving assignment problems in Excel.

Reiteration: Mastering Excel for problem-solving offers numerous benefits, including improved data analysis, better decision-making, and enhanced project management skills. By honing your Excel skills, you can excel in your professional and academic endeavors.

Immediate Download

MAC & PC Compatible

Free Email Support

Related aticles

The Benefits of Excel Dashboards for Data Analysts

Unlock the Power of Real-Time Data Visualization with Excel Dashboards

Unlocking the Potential of Excel's Data Dashboard

Unleashing the Benefits of a Dashboard with Maximum Impact in Excel

Exploring Data Easily and Securely: Essential Features for Excel Dashboards

Unlock the Benefits of Real-Time Dashboard Updates in Excel

Unleashing the Power of Excel Dashboards

Understanding the Benefits and Challenges of Excel Dashboard Design and Development

Leverage Your Data with Excel Dashboards

Crafting the Perfect Dashboard for Excel

An Introduction to Excel Dashboards

How to Create an Effective Excel Dashboard

• Choosing a selection results in a full page refresh.