

Mathematics
- Algebraic Expressions
- Linear Equations
- Parametric Equations
- Absolute-value Equations
- Sets of Equations
- Practical Problems
- Linear Inequations
- Linear Inequations - Tab
- Quadratic Equations
- Quadratic Equation by Discussion
- Quadratic Equation - Roots Properties
- Irrational Equations
- Quadratic Inequalities
- Absolute Value
- Exponential Equations
- Logarithms - Basics
- Logarithmic Exponential Equations
- Logarithmic Equations - Other Bases
- Quadratic Logarithmic Equations
- Sets of Logarithmic Equations
- Expressions
- Súčtové a rozdielové vzorce
- Dvojnásobný a polovičný argument
- Arithmetic Progression
- Geometric Progression
- Factorial & Binomial Coefficient
- Binomial Theorem
- Permutations (general)
- Permutations
Combinations
- Probability
- Right Triangle
1. Characterize combinations and combinations with repetition.
2. On the plane there are 6 different points (no 3 of them are lying on the same line). How many segments do you get by joining all the points?
3. On a circle there are 9 points selected. How many triangles with edges in these points exist?
4. a) Find out a formula for counting the number of diagonals in a convex n-gon! b) How many diagonals has a 10-gon?
5. In how many ways you can choose 8 of 32 playing cards not considering their order?
The playing cards can be chosen in 10 518 300 ways.
6. A teacher has prepared 20 arithmetics tasks and 30 geometry tasks. For a test he‘d like to use:
7. On a graduation party the graduants pinged their glasses. There were 253 pings. How many graduants came to the party?
8. If the number of elements would raise by 8, number of combinations with k=2 without repetition would raise 11 times. How many elements are there?
9. For which x positive integer stands:
10. Two groups consist of 26 elements and 160 combinations without repetition for k=2 together. How many elements are in the first and how many in the second group?
11. In the confectioners 5 different icecreams are sold. A father would like to buy 15 caps of icecream for his family. In how many ways can he buy the icecream?
12. From how many elements 15 combinations with repetition (k=2) can be made?
Adblock detected
Vážený návštevník Priklady.eu, našim systémom bolo detekované odmietnutie zobrazenie reklamy. Na vašom počítači je teda veľmi pravdepodobne nainštalovaný softvér slúžiaci na blokovanie reklám. Reklamy sú pre nás jediným zdrojom príjmov, čo nám umožňuje poskytovať Vám obsah bez poplatkov, zadarmo. Prosíme, odblokujte ho. Povolenie reklamy na tejto stránke je možné docieliť aktiváciou voľby "Nespúšťať Adblock na stránkach na tejto doméne", alebo "Vypnúť Adblock na priklady.eu", prípadne inú podobnú položkou v menu vášho programu na blokovanie reklám. Ďakujeme za pochopenie, tím Priklady.eu. Vážený návštěvníku Priklady.eu, našim systémem bylo detekováno odmítnutí zobrazení reklamy. Na vašem počítači je tedy velice pravděpodobně nainstalován software sloužící k blokování reklam. Reklamy jsou pro nás jediným zdrojem příjmů, což nám umožňuje Vám poskytovat obsah bez poplatků, zdarma. Prosíme, odblokujte je. Povolení reklamy na této stránce lze docílit aktivací volby "Nespouštět AdBlock na stránkách na této doméně", nebo "Vypnout AdBlock na priklady.eu", případně jinou podobnou položkou v menu vašeho programu na blokování reklam. Děkujeme za pochopení, tým Priklady.eu.
Reset password New user? Sign up
Existing user? Log in
Combinations
Already have an account? Log in here.
- Paul Ryan Longhas
- Gene Keun Chung
- A Former Brilliant Member
A combination is a way of choosing elements from a set in which order does not matter. A wide variety of counting problems can be cast in terms of the simple concept of combinations, therefore, this topic serves as a building block in solving a wide range of problems.
Introduction
Basic examples, intermediate examples, advanced examples, combinations with repetition, combinations with restriction, combinations - problem solving.
Consider the following example: Lisa has \(12\) different ornaments and she wants to give \(5\) ornaments to her mom as a birthday gift (the order of the gifts does not matter). How many ways can she do this?
We can think of Lisa giving her mom a first ornament, a second ornament, a third ornament, etc. This can be done in \( \frac{12!}{7!} \) ways. However, Lisa’s mom is receiving all five ornaments at once, so the order Lisa decides on the ornaments does not matter. There are \( 5! \) reorderings of the chosen ornaments, implying the total number of ways for Lisa to give her mom an unordered set of \(5\) ornaments is \( \frac{12!}{7!5!} \).
Notice that in the answer, the factorials in the denominator sum to the value in the numerator. This is not a coincidence. In general, the number of ways to pick \( k \) unordered elements from an \( n \) element set is \( \frac{n!}{k!(n-k)!} \). This is a binomial coefficient.
Proof of \(\displaystyle {n \choose k} = \frac{n!}{k!(n-k)!}:\)
Now suppose we want to choose \(k\) objects from \(n\) objects, then the number of combinations of \(k\) objects chosen from \(n\) objects is denoted by \(n \choose k\). Since \({_nP_k}=k!{n \choose k}\), it follows that
\[{n \choose k} = \frac{1}{k!}(_nP_k)= \frac{n!}{k!(n-k)!}.\]
How many ways are there to arrange 3 chocolate chip cookies and 10 raspberry cheesecake cookies into a row of 13 cookies? We can consider the situation as having 13 spots and filling them with 3 chocolate chip cookies and 10 raspberry cheesecake cookies. Then we just choose 3 spots for the chocolate chip cookies and let the other 10 spots have raspberry cheesecake cookies. The number of ways to do this job is \({13\choose3}=\frac{13\times12\times11}{3\times2\times1}=286.\) \(_\square\)
Out of 7 consonants and 4 vowels, how many words of 3 consonants and 2 vowels can be formed? The number of ways of selecting 3 consonants out of 7 and 2 vowels out of 4 is \({7\choose3}\times{4\choose2} = 210.\) Therefore, the number of groups each containing 3 consonants and 2 vowels is \(210.\) Since each group contains 5 letters, which can be arranged amongst themselves in \(5!= 120\) ways, the required number of words is \(210\times120 = 25200.\ _\square\)
How many ways are there to select 3 males and 2 females out of 7 males and 5 females? The number of ways to select \(3\) males out of \(7\) is \({7 \choose 3} = \frac{7\times 6\times 5}{3 \times 2 \times 1}=35.\) Similarly, the number of ways to select \(2\) females out of \(5\) is \({5 \choose 2} = \frac{5\times 4}{2 \times 1}=10.\) Hence, by the rule of product, the answer is \(35 \times 10=350\) ways. \(_\square\)
There are \(9\) children. How many ways are there to group these \(9\) children into 2, 3, and 4? The number of ways to choose \(2\) children out of \(9\) is \({9\choose2}=\frac{9 \times 8}{2 \times 1}=36.\) The number of ways to choose \(3\) children out of \(9-2=7\) is \({7 \choose 3}=\frac{7 \times 6 \times 5}{3 \times 2 \times 1}=35.\) Finally, the number of ways to choose \(4\) children out of \(7-3=4\) is \({4 \choose 4}=1.\) Hence, by the rule of product, the answer is \(36 \times 35 \times 1=1260\) ways. \(_\square\)
There are \(9\) distinct chairs. How many ways are there to group these chairs into 3 groups of 3? The number of ways to choose \(3\) chairs out of \(9\) is \({9\choose3}=\frac{9 \times 8 \times 7}{3 \times 2 \times 1}=84.\) The number of ways to choose \(3\) chairs out of \(9-3=6\) is \({6 \choose 3}=\frac{6 \times 5 \times 4}{3 \times 2 \times 1}=20.\) Finally, the number of ways to choose \(3\) chairs out of \(6-3=3\) is \({3 \choose 3}=1.\) Now, since each of these three groups has an equal number of three chairs and the order of the three groups does not matter, by the rule of product our answer is \[\frac{84 \times 20 \times 1}{3 !}=280\] ways. \(_\square\)
At a party, everyone shook hands with everybody else. There were 66 handshakes. How many people were at the party?
A combination is a way of choosing elements from a set in which order does not matter.
In general, the number of ways to pick \( k \) unordered elements from an \( n \) element set is \( \frac{n!}{k!(n-k)!} \). This is a binomial coefficient , denoted \( n \choose k \).
How many ordered non-negative integer solutions \( (a, b, c, d) \) are there to the equation \( a + b + c + d = 10 \)? To solve this problem, we use a technique called "stars and bars," which was popularized by William Feller. We create a bijection between the solutions to \( a + b + c + d = 10 \) and sequences of 13 digits, consisting of ten 1's and three 0's. Given a set of four integers whose sum is 10, we create a sequence that starts with \( a \) 1's, then has a 0, then has \( b \) 1's, then has a 0, then has \( c \) 1's, then has a 0, and then has \( d \) 1's. Conversely, given such a sequence, we can set \( a \) to be equal to the length of the initial string of 1's (before the first 0), set \( b \) equal to the length of the next string of 1's (between the first and second 0), set \( c \) equal to the length of the third string of 1's (between the second and third 0), and set \( d \) equal to the length of the fourth string of 1's. It is clear that such a procedure returns the starting set, and hence we have a bijection. Now, it remains to count the number of such sequences. We pick 3 positions for the 0's and the remaining positions are 1's. Hence, there are \( {13 \choose 3}= 286 \) such sequences. \(_\square\)
There are \(5\) shirts all of different colors, \(4\) pairs of pants all of different colors, and \(2\) pairs of shoes with different colors. In how many ways can Amy and Bunny be dressed up with a shirt, a pair of pants, and a pair of shoes each? We choose \(2\) shirts out of \(5\) for both Amy and Bunny to wear, so \({5\choose2}2!=20.\) We choose \(2\) pairs of pants out of \(4\) for them to wear, so \({4\choose2}2!=12.\) We choose \(2\) pairs of shoes out of \(2\) for them to wear, so \({2\choose2}2!=2.\) Therefore, by the rule of product, the answer is \(20 \times 12 \times 2=480\) ways. \(_\square\)
We are trying to divide 5 European countries and 5 African countries into 5 groups of 2 each. How many ways are there to do this under the restriction that at least one group must have only European countries? The number of ways to divide \(5+5=10\) countries into 5 groups of 2 each is as follows: \[\frac{{10\choose2} \times {8\choose2} \times {6\choose2} \times {4\choose2} \times {2\choose2}}{5 !} =\frac{ 45 \times 28 \times 15 \times 6 \times 1}{120}=945. \qquad (1)\] Since it is required that at least one group must have only European countries, we need to subtract from \((1)\) the number of possible groupings where all 5 groups have 1 European country and 1 African country each. This is equivalent to the number of ways to match each of the 5 European countries with one African country: \[5 ! = 5 \times 4 \times 3 \times 2 \times 1=120. \qquad (2)\] Therefore, taking \((1)-(2)\) gives our answer \(945-120=825.\) \(_\square\)
Find the number of rectangles in a \(10 \times 12\) chessboard.
Note: All squares are rectangles, but not all rectangles are squares.
There are two distinct boxes, 10 identical red balls, 10 identical yellow balls, and 10 identical blue balls. How many ways are there to sort the 30 balls into the two boxes so that each box has 15? Keeping in mind that the two boxes are distinct, let \(r, y\) and \(b\) be the numbers of red, yellow and blue balls in the first box, respectively. Then we first need to get the number of cases satisfying \(r+y+b=15,\) and then subtract the numbers of cases where \(r>10, y>10\) or \(b>10.\) Using stars and bars, the number of cases satisfying \(r+y+b=15\) is \({17\choose2}=136. \qquad (1)\) Now, the following gives the number of cases where \(10<r\le15:\) If \(r=11,\) then \(y+b=4,\) implying there are 5 such cases. If \(r=12,\) then \(y+b=3,\) implying there are 4 such cases. If \(r=13,\) then \(y+b=2,\) implying there are 3 such cases. If \(r=14,\) then \(y+b=1,\) implying there are 2 such cases. If \(r=15,\) then \(y+b=0,\) implying there is 1 such case. Hence, the number cases where \(10<r\le15\) is \(5+4+3+2+1=15.\) Since exactly the same logic applies for the cases where \(10<y\le15\) or \(10<b\le15,\) the total number of cases to subtract from \((1)\) is \(3\times 15=45. \qquad (2)\) Therefore, taking \((1)-(2)\) gives our answer \(136-45=91.\) \(_\square\)
PizzaHot makes 7 kinds of pizza, 3 of which are on sale everyday, 7 days a week. According to their policy, any two kinds of pizza that are on sale on a same day can never be on sale on the same day again during the rest of that calender week. Let \(X\) be the number of all the possible sale strategies during a calendar week. What is the remainder of \(X\) upon division by 1000? Let \(a, b, c, d, e, f, g\) be the 7 kinds of pizza. Then none of these 7 could be on sale for 4 days or more a week because each of the other 6 kinds would have been on sale on a same day in the first 3 days. In fact, since there are \(3\times 7=21\) pizzas on sale every week, each of the 7 kinds is on sale exactly 3 times a week. Now, without loss of generality, the number of ways to select 3 days to put \(a\) on sale is \({7\choose 3}.\) Then the number of ways to put each of the remaining 6 kinds on sale in those 3 days is \({6\choose 2}\times {4\choose 2}\times {2\choose 2} .\) The following table is one example of this operation, where \(a\) is on sale for all 3 days during the week, whereas each of the other 6 kinds is on sale only once: pizza Since we are done with \(a,\) we now put one \(b\) in each of 2 of the remaining 4 days, the number of ways of doing which is \({4 \choose 2}.\) Then, excluding \(c\) which was already on sale together with \(b\) on the first day, we put \(d, e, f, g\) in the 2 days where \(b\) was just put. However, since the combinations \((d, e)\) and \((f, g)\) were already used when dealing with \(a,\) the number of ways to put \(d, e, f, g\) in the two columns together with \(b\) is \({4 \choose 2}-2.\) Finally, we put one \(c\) in each of the remaining two columns and then fill the columns, the number of ways of doing which is 2. Hence, the number of all the possible sale strategies during a calendar week is \[{7\choose 3}\times {6\choose 2}\times {4\choose 2}\times {4\choose 2}\times\left({4 \choose 2}-2\right)\times 2=151200.\] Therefore, the remainder of \(151200\) upon division by 1000 is 200. \(_\square\)
Three squares are chosen at random on a chess board. Find the probability that they lie on any diagonal.
\(\) Note: A line connecting the three squares \((1,1), (2,3), (3,5)\) does not form a diagonal.
\(A\) and \(B\) are the only candidates who contest in an election. They secure \(11\) and \(7\) votes, respectively. In how many ways can this happen if it is known that \(A\) stayed ahead of \(B\) throughout the counting process of votes?
Main Article: Combinations with Repetition
You want to distribute 7 indistinguishable candies to 4 kids. If every kid must receive at least one candy, in how many ways can you do this? You first give one candy to each of the 4 kids to comply with the requirement that every kid must receive at least one candy. Then you are left with 3 candies to distribute to the 4 kids, which is equivalent to a problem of placing \(k=3\) indistinguishable balls into \(n=4\) labeled urns, which is known as balls and urns or stars and bars. Thus, our answer is \[\binom{n+k-1}{k} =\binom{n+k-1}{n-1}=\binom{3+4-1}{3}=20. \ _\square \]
Winston must choose 4 classes for his final semester of school. He must take at least 1 science class and at least 1 arts class. If his school offers 4 (distinct) science classes, 3 (distinct) arts classes and 3 other (distinct) classes, how many different choices for classes does he have?
\(\) Details and Assumptions:
- He cannot take the same class twice.
How many six digit integers contain exactly four different digits?
Try more combinatorics problems.
Let \(x+y+z=m,\) where \(x, y, z\) are integers such that \(x\ge 1, y\ge 2, z\ge 3.\) If the number of ordered triples \((x, y, z)\) satisfying the equation is \(21,\) what is \(m?\) Let \(x-1=a, y-2=b, z-3=c,\) where \(a, b, c\) are non-negative because \(x\ge 1, y\ge 2, z\ge 3,\) then \[\begin{align} x+y+z&=m\\ (a+1)+(b+2)+(c+3)&=m\\ a+b+c&=m-6. \qquad (1) \end{align}\] Since the number of ordered non-negative integer triples \((a, b, c)\) satisfying \((1)\) is \(21,\) using the technique of stars and bars , we obtain \[\begin{align} \binom{3+(m-6)-1}{m-6} =\binom{m-4}{m-6}=\binom{m-4}{2}&=21\\ \frac{(m-4)(m-5)}{2!}&=21\\ m^2-9m+20&=42\\ m^2-9m-22&=0\\ (m+2)(m-11)&=0\\ m&=11 \end{align}\] because \(m>0.\ _\square\)
How many ways are there to select \(3\) numbers from the first \(20\) positive integers such that no 2 of the selected numbers are consecutive?
In the figure above with 9 squares, how many ways are there to select two squares which do not share an edge?
This problem is part of the set Countings.
Suppose a small country has \(15\) cities and \(70\) roads, where each road directly connects precisely \(2\) cities. What is the largest possible number of cities that are directly connected to every other city in the country?
A pawn is placed on the lower left corner square of a standard \(8\) by \(8\) chess board. A 'move' involves moving the pawn, where possible, either
- one square to the right,
- one square up, or
- diagonally (one square up and to the right).
Using these legitimate moves, the pawn is to be moved along a path from the lower left square to the upper right square.
How many such paths are there?
Problem Loading...
Note Loading...
Set Loading...

Combinations – Example and Practice Problems
Combinations are used to count the number of different ways that certain groups can be chosen from a set if the order of the objects does not matter. This is different from permutations, where the order of the objects does matter.
Here, we will look at a brief summary of combinations along with their formula and the terminology used. In addition, we will see examples with answers to learn about the application of the combination formula.
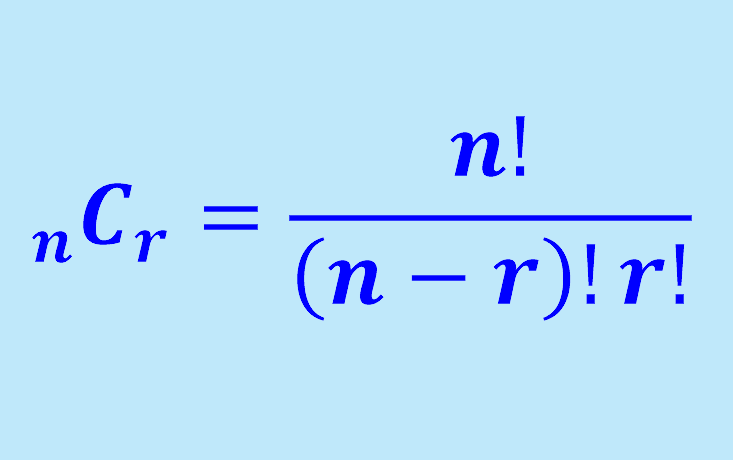
Relevant for …
Learning about combinations with solved examples.
See examples
Summary of combinations
Combinations – examples with answers, combinations – practice problems.
Combinations are selections of objects in a collection, in which the order of the selection does not matter. In combinations, we can select the objects in any order. For example, if we have ab and ba , these selections are considered equal in combinations.
The formula to determine the number of possible organizations by selecting a few objects from a set without repetitions is expressed in the following way:
| $latex _{n}{{C}_{k}}=\frac{{n!}}{{\left( {n-k} \right)!k!}}$ |
- n is the total number of elements in a set
- k is the number of selected objects
- ! is the factorial symbol
Recall that the factorial (denoted as “!”) is a product of all positive integers less than or equal to the number preceding the factorial. For example, $latex 3!=1 \times 2 \times 3 = 6$.
With the following examples, you can practice applying the combination formula. Each exercise has its respective solution to analyze the reasoning behind each answer.
Find the result of the combination $latex _{8}C_{6}$.
We use the formula of combinations $latex _{n}{{C}_{k}}=\frac{{n!}}{{\left( {n-k} \right)!k!}}$ and substitute $latex n=8$ and $latex k=6$:
$latex _{8}{{C}_{6}}=\frac{{8!}}{{\left( {8-6} \right)!6!}}$
$latex =\frac{{8!}}{{\left( {2} \right)!6!}}$
Now, we recognize that we can write to 8! like $latex 8 \times 7 \times 6!$ and we eliminate 6! both in the numerator and in the denominator:
$latex \frac{{8!}}{{\left( {2} \right)!6!}}=\frac{{8\times 7}}{2}$
$latex =4\times 7=28$
Find the result of the combination $latex _{9}C_{4}$.
We substitute $latex n=9$ and $latex k=4$ in the formula $latex _{n}{{C}_{k}}=\frac{{n!}}{{\left( {n-k} \right)!k!}}$:
$latex _{9}{{C}_{4}}=\frac{{9!}}{{\left( {9-4} \right)!4!}}$
$latex =\frac{{9!}}{{\left( {5} \right)!4!}}$
Now, we recognize that we can write to 9! like $latex 9\times 8\times 7\times 6\times 5!$ and we eliminate 5! both in the numerator and in the denominator:
$latex \frac{{9!}}{{\left( {5} \right)!4!}}=\frac{{9\times 8\times 7\times 6}}{4!}$
We rewrite 4! like $latex 4\times 3\times 2\times 1$ and simplify:
$latex \frac{{9\times 8\times 7\times 6}}{4\times 3\times 2\times 1}=126$
Find the combination $latex _{100}C_{100}$.
We substitute $latex n=100$ and $latex k=100$ in the formula $latex _{n}{{C}_{k}}=\frac{{n!}}{{\left( {n-k} \right)!k!}}$:
$latex _{100}{{C}_{100}}=\frac{{100!}}{{\left( {100-100} \right)!100!}}$
$latex =\frac{{100!}}{{\left( {1} \right)!100!}}$
We can easily eliminate 100! both denominator and numerator:
$latex \frac{{100!}}{{\left( {1} \right)!100!}}=1$
This result makes sense since there is only one possible way to select 100 objects from a set of 100 objects if the order does not matter.
How many ways are there to choose a team of 3 from a group of 10?
In this case, we choose 3 people so we have $latex k=3$. The whole group is $latex n=10$. Using this data in the formula $latex _{n}{{C}_{k}}=\frac{{n!}}{{\left( {n-k} \right)!k!}}$, we have:
$latex _{10}{{C}_{3}}=\frac{{10!}}{{\left( {10-3} \right)!3!}}$
$latex =\frac{{10!}}{{\left( {7} \right)!3!}}$
We can expand the 10! until you get 7! and we simplify this:
$latex \frac{10!}{(3)!3!}=\frac{10\times 9 \times 8 \times 7!}{(7)!3!}$
$latex =\frac{{10\times 9 \times 8}}{{3!}}$
$latex =\frac{{10\times 9 \times 8}}{{6}}$
$latex =120$
Suppose we have to select 5 new employees from a list of 10 applicants. In how many ways can this be done?
In this case, we have $latex n=10$ and $latex k=5$, therefore, we have:
$latex _{10}{{C}_{5}}=\frac{{10!}}{{\left( {10-5} \right)!5!}}$
$latex =\frac{{10!}}{{\left( {5} \right)!5!}}$
We can rewrite 10! until we get 5! and simplify:
$latex \frac{{10!}}{{\left( {5} \right)!5!}}=\frac{{10 \times 9\times 8 \times 7 \times 6 \times 5!}}{{\left( {5} \right)!5!}}$
$latex =\frac{{10 \times 9\times 8 \times 7 \times 6}}{{5!}}$
$latex =\frac{10 \times 9\times 8 \times 7 \times 6}{5 \times 4\times 3 \times 2 \times 1}$
$latex =252$
In a car dealership, there are 3 cars of a particular model that have to be transported to another dealership. If there are a total of 25 cars of this model, how many options are available to transport?
We recognize that we have $latex n=25$ y $latex k=3$ and we substitute these values in the formula $latex _{n}{{C}_{k}}=\frac{{n!}}{{\left( {n-k} \right)!k!}}$:
$latex _{25}{{C}_{3}}=\frac{{25!}}{{\left( {25-3} \right)!3!}}$
$latex =\frac{{25!}}{{\left( {22} \right)!3!}}$
We rewrite the factorial 25! until we get to 22!:
$latex \frac{{25!}}{{\left( {22} \right)!3!}}=\frac{{25 \times 24 \times 23 \times 22!}}{{\left( {22} \right)!3!}}$
Now, we simplify to 22! in the numerator and denominator:
$latex \frac{{25 \times 24 \times 23 \times 22!}}{{\left( {22} \right)!3!}}=\frac{{25 \times 24 \times 23}}{{3!}}$
$latex =25 \times 4 \times 23=2300$
Suppose we have an office of 5 women and 6 men and we have to select a committee of 4 people. In how many ways can we select 2 men and 2 women?
In this case, we have to find two different combinations and then multiply them. Therefore, we want to calculate $latex (_{5}{{C}_{2}})(_{6}{{C}_{2}})$. We can calculate these combinations separately:
$latex _{5}{{C}_{2}}=\frac{{5!}}{{\left( {5-2} \right)!2!}}$
$latex =\frac{{5!}}{{\left( {3} \right)!2!}}$
$latex =\frac{{5\times 4\times 3!}}{{\left( {3} \right)!2!}}$
$latex =\frac{{5\times 4}}{{2!}}=10$
$latex _{6}{{C}_{2}}=\frac{{6!}}{{\left( {6-2} \right)!2!}}$
$latex =\frac{{6!}}{{\left( {4} \right)!2!}}$
$latex =\frac{{6\times 5\times 4!}}{{\left( {4} \right)!2!}}$
$latex =\frac{{6\times 5}}{{2!}}=15$
Therefore, we have $latex (_{5}{{C}_{2}})(_{6}{{C}_{2}})=10\times 15=150$.
→ Combinations Calculator (nCr)
Put your knowledge of combinations into practice with the following problems. Solve the combinations and select an answer. Please check it to make sure you selected the correct one.
Find the combination $latex _{9}C_{5}$.
Choose an answer
Find the combinations $latex _{11}C_{9}$.
How many combinations are there if we take 2 objects from a set of 7, we want to choose a team of 6 out of a pool of 9. how many ways are there to accomplish this, there are 10 people in a meeting. if everyone shakes hands, how many handshakes are possible.
Interested in learning more about factorials, permutations, and combinations? Take a look at these pages:
- Combinations Calculator (nCr)
- Examples of Factorials
- Examples of Permutations

Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.

Learn mathematics with our additional resources in different topics

Copyright © 2024 Neurochispas
All rights reserved.
INFORMATION
Terms and Conditions
Privacy Policy
About Neurochispas
About the Author

Child Login
- Kindergarten
- Number charts
- Skip Counting
- Place Value
- Number Lines
- Subtraction
- Multiplication
- Word Problems
- Comparing Numbers
- Ordering Numbers
- Odd and Even
- Prime and Composite
- Roman Numerals
- Ordinal Numbers
- In and Out Boxes
- Number System Conversions
- More Number Sense Worksheets
- Size Comparison
- Measuring Length
- Metric Unit Conversion
- Customary Unit Conversion
- Temperature
- More Measurement Worksheets
- Writing Checks
- Profit and Loss
- Simple Interest
- Compound Interest
- Tally Marks
- Mean, Median, Mode, Range
- Mean Absolute Deviation
- Stem-and-leaf Plot
- Box-and-whisker Plot
- Permutation and Combination
- Probability
- Venn Diagram
- More Statistics Worksheets
- Shapes - 2D
- Shapes - 3D
- Lines, Rays and Line Segments
- Points, Lines and Planes
- Transformation
- Quadrilateral
- Ordered Pairs
- Midpoint Formula
- Distance Formula
- Parallel, Perpendicular and Intersecting Lines
- Scale Factor
- Surface Area
- Pythagorean Theorem
- More Geometry Worksheets
- Converting between Fractions and Decimals
- Significant Figures
- Convert between Fractions, Decimals, and Percents
- Proportions
- Direct and Inverse Variation
- Order of Operations
- Squaring Numbers
- Square Roots
- Scientific Notations
- Speed, Distance, and Time
- Absolute Value
- More Pre-Algebra Worksheets
- Translating Algebraic Phrases
- Evaluating Algebraic Expressions
- Simplifying Algebraic Expressions
- Algebraic Identities
- Quadratic Equations
- Systems of Equations
- Polynomials
- Inequalities
- Sequence and Series
- Complex Numbers
- More Algebra Worksheets
- Trigonometry
- Math Workbooks
- English Language Arts
- Summer Review Packets
- Social Studies
- Holidays and Events
- Worksheets >
- Statistics >
- Combination
Combination Worksheets
Combination is a selection of distinct elements without specific orders. Combination worksheets are diligently prepared as per the state standards and proposed for high school students. Unearth the usage of combinations in real-world scenarios with this array of printable exercises, like listing out combinations, finding the number of combinations, evaluation, solving combination problems and more.We also have a huge collection of permutation worksheets for practice. Practice some of these worksheets for free!

Listing Out Combinations
Jot down all the possible combinations of the habitual elements like names, numbers, shapes, alphabets, colors and so on!
- Download the set

Number of Combinations
Write down the total number of possible combinations for a set of objects taken at a time. Each pdf worksheet consists of five problems.

Evaluate - Level 1
These printable high school worksheets include problems with simple expressions involving combinations. Students are required to simplify the expressions using the combination formula.

Evaluate - Level 2
Level 2 worksheets include more integrative problems involving basic operations. Using the formula for C(n, r), evaluate the expressions.

Solve - Level 1
Access this set of pdf combination worksheets to find the unknown value in the equations using the formula for C(n, r).

Solve - Level 2
These printable Level 2 worksheets encompass challenging problems when compared to level 1 worksheets. Solve problems using the combination formula to know the unknown parameters.

Permutation and Combination - Mixed Review
These permutations and combinations worksheets consist of an array of exercises to identify and write permutations / combinations, twin-level of solving equations and evaluating expressions.
(15 Worksheets)
Related Worksheets
» Factorial
» Permutation
» Permutation and Combination
Become a Member
Membership Information
Privacy Policy
What's New?
Printing Help
Testimonial
Copyright © 2024 - Math Worksheets 4 Kids
This is a members-only feature!

Combinations and Permutations
What's the difference.
In English we use the word "combination" loosely, without thinking if the order of things is important. In other words:
"My fruit salad is a combination of apples, grapes and bananas" We don't care what order the fruits are in, they could also be "bananas, grapes and apples" or "grapes, apples and bananas", its the same fruit salad.
"The combination to the safe is 472" . Now we do care about the order. "724" won't work, nor will "247". It has to be exactly 4-7-2 .
So, in Mathematics we use more precise language:
- When the order doesn't matter, it is a Combination .
- When the order does matter it is a Permutation .
|
So, we should really call this a "Permutation Lock"! |
In other words:
A Permutation is an ordered Combination.
| To help you to remember, think " ermutation ... osition" |
Permutations
There are basically two types of permutation:
- Repetition is Allowed : such as the lock above. It could be "333".
- No Repetition : for example the first three people in a running race. You can't be first and second.
1. Permutations with Repetition
These are the easiest to calculate.
When a thing has n different types ... we have n choices each time!
For example: choosing 3 of those things, the permutations are:
n × n × n (n multiplied 3 times)
More generally: choosing r of something that has n different types, the permutations are:
n × n × ... (r times)
(In other words, there are n possibilities for the first choice, THEN there are n possibilites for the second choice, and so on, multplying each time.)
Which is easier to write down using an exponent of r :
n × n × ... (r times) = n r
Example: in the lock above, there are 10 numbers to choose from (0,1,2,3,4,5,6,7,8,9) and we choose 3 of them:
10 × 10 × ... (3 times) = 10 3 = 1,000 permutations
So, the formula is simply:
| where is the number of things to choose from, and we choose of them, repetition is allowed, and order matters. |
2. Permutations without Repetition
In this case, we have to reduce the number of available choices each time.

Example: what order could 16 pool balls be in?
After choosing, say, number "14" we can't choose it again.
So, our first choice has 16 possibilites, and our next choice has 15 possibilities, then 14, 13, 12, 11, ... etc. And the total permutations are:
16 × 15 × 14 × 13 × ... = 20,922,789,888,000
But maybe we don't want to choose them all, just 3 of them, and that is then:
16 × 15 × 14 = 3,360
In other words, there are 3,360 different ways that 3 pool balls could be arranged out of 16 balls.
Without repetition our choices get reduced each time.
But how do we write that mathematically? Answer: we use the " factorial function "
| ! | The (symbol: !) just means to multiply a series of descending natural numbers. Examples: |
| Note: it is generally agreed that . It may seem funny that multiplying no numbers together gets us 1, but it helps simplify a lot of equations. | |
So, when we want to select all of the billiard balls the permutations are:
16! = 20,922,789,888,000
But when we want to select just 3 we don't want to multiply after 14. How do we do that? There is a neat trick: we divide by 13!
16 × 15 × 14 × 13 × 12 × ... 13 × 12 × ... = 16 × 15 × 14
That was neat: the 13 × 12 × ... etc gets "cancelled out", leaving only 16 × 15 × 14 .
The formula is written:
|
|
| where is the number of things to choose from, and we choose of them, no repetitions, order matters. |
Example Our "order of 3 out of 16 pool balls example" is:
(which is just the same as: 16 × 15 × 14 = 3,360 )
Example: How many ways can first and second place be awarded to 10 people?
(which is just the same as: 10 × 9 = 90 )
Instead of writing the whole formula, people use different notations such as these:
- P(10,2) = 90
- 10 P 2 = 90
Combinations
There are also two types of combinations (remember the order does not matter now):
- Repetition is Allowed : such as coins in your pocket (5,5,5,10,10)
- No Repetition : such as lottery numbers (2,14,15,27,30,33)
1. Combinations with Repetition
Actually, these are the hardest to explain, so we will come back to this later.
2. Combinations without Repetition
This is how lotteries work. The numbers are drawn one at a time, and if we have the lucky numbers (no matter what order) we win!
The easiest way to explain it is to:
- assume that the order does matter (ie permutations),
- then alter it so the order does not matter.
Going back to our pool ball example, let's say we just want to know which 3 pool balls are chosen, not the order.
We already know that 3 out of 16 gave us 3,360 permutations.
But many of those are the same to us now, because we don't care what order!
For example, let us say balls 1, 2 and 3 are chosen. These are the possibilites:
| Order does matter | Order doesn't matter |
| 1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1 | 1 2 3 |
So, the permutations have 6 times as many possibilites.
In fact there is an easy way to work out how many ways "1 2 3" could be placed in order, and we have already talked about it. The answer is:
3! = 3 × 2 × 1 = 6
(Another example: 4 things can be placed in 4! = 4 × 3 × 2 × 1 = 24 different ways, try it for yourself!)
So we adjust our permutations formula to reduce it by how many ways the objects could be in order (because we aren't interested in their order any more):
That formula is so important it is often just written in big parentheses like this:
| = ( ) |
| where is the number of things to choose from, and we choose of them, no repetition, order doesn't matter. |
It is often called "n choose r" (such as "16 choose 3")
And is also known as the Binomial Coefficient .
All these notations mean "n choose r":
Just remember the formula:
n! r!(n − r)!
Example: Pool Balls (without order)
So, our pool ball example (now without order) is:
16! 3!(16−3)!
= 16! 3! × 13!
= 20,922,789,888,000 6 × 6,227,020,800
Notice the formula 16! 3! × 13! gives the same answer as 16! 13! × 3!
So choosing 3 balls out of 16, or choosing 13 balls out of 16, have the same number of combinations:
16! 3!(16−3)! = 16! 13!(16−13)! = 16! 3! × 13! = 560
In fact the formula is nice and symmetrical :
Also, knowing that 16!/13! reduces to 16×15×14, we can save lots of calculation by doing it this way:
16×15×14 3×2×1
Pascal's Triangle
We can also use Pascal's Triangle to find the values. Go down to row "n" (the top row is 0), and then along "r" places and the value there is our answer. Here is an extract showing row 16:
OK, now we can tackle this one ...

Let us say there are five flavors of icecream: banana, chocolate, lemon, strawberry and vanilla .
We can have three scoops. How many variations will there be?
Let's use letters for the flavors: {b, c, l, s, v}. Example selections include
- {c, c, c} (3 scoops of chocolate)
- {b, l, v} (one each of banana, lemon and vanilla)
- {b, v, v} (one of banana, two of vanilla)
(And just to be clear: There are n=5 things to choose from, we choose r=3 of them, order does not matter, and we can repeat!)
Now, I can't describe directly to you how to calculate this, but I can show you a special technique that lets you work it out.
Think about the ice cream being in boxes, we could say "move past the first box, then take 3 scoops, then move along 3 more boxes to the end" and we will have 3 scoops of chocolate!
So it is like we are ordering a robot to get our ice cream, but it doesn't change anything, we still get what we want.
In fact the three examples above can be written like this:
| {c, c, c} (3 scoops of chocolate): | |
| {b, l, v} (one each of banana, lemon and vanilla): | |
| {b, v, v} (one of banana, two of vanilla): |
So instead of worrying about different flavors, we have a simpler question: "how many different ways can we arrange arrows and circles?"
Notice that there are always 3 circles (3 scoops of ice cream) and 4 arrows (we need to move 4 times to go from the 1st to 5th container).
So (being general here) there are r + (n−1) positions, and we want to choose r of them to have circles.
This is like saying "we have r + (n−1) pool balls and want to choose r of them". In other words it is now like the pool balls question, but with slightly changed numbers. And we can write it like this:
| = ( ) |
| where is the number of things to choose from, and we choose of them repetition allowed, order doesn't matter. |
Interestingly, we can look at the arrows instead of the circles, and say "we have r + (n−1) positions and want to choose (n−1) of them to have arrows", and the answer is the same:
So, what about our example, what is the answer?
There are 35 ways of having 3 scoops from five flavors of icecream.
In Conclusion
Phew, that was a lot to absorb, so maybe you could read it again to be sure!
But knowing how these formulas work is only half the battle. Figuring out how to interpret a real world situation can be quite hard.
But at least you now know the 4 variations of "Order does/does not matter" and "Repeats are/are not allowed":
| Repeats allowed | No Repeats | |
|---|---|---|
| Permutations (order matters): | n | |
| Combinations (order doesn't matter): |
Combinations and Probability
Related Topics: More Lessons for College Algebra Math Worksheets
A series of college algebra lectures: Solving Problems Involving Permutations, Solving Problems Involving Combinations, Independent Events, Inclusive Events
Solving Problems Involving Permutations Examples:
- A museum has 7 paintings by Picasso and wants to arrange 3 of them on the same wall. How many ways are there to do this?
- How many ways can you arrange the letters in the word LOLLIPOP?
Permutation & Combination Application/Word Problems Example:
- In how many ways can a president and a vice president be selected from a committee of 32 people.
- An organization with 23 members is to select 7 chairman, with each member having equal authority. In how many ways can this be done?
- A club consists of 12 men and 15 women. In how many ways can this club choose a president, vice-president, treasurer, and secretary along with an advisory committee of 5 people?
- A state allows personalized license plates with 6 spaces. These spaces can be filled either with numbers 0 - 19, letters A - Z, or any of the following symbols: β, η, −, δ, ϕ. What is the total number of personalized license plates that could possibly be made using this counting scheme?
- A student answers 8 out of 10 questions on an exam. How many different ways can the selected 8 questions be answered?
- A typical social security number looks as follows: 777-93-1111. How many social security numbers can be made up if you restrict the first 2 digits from being zero and the last 2 digits from being zero or nine?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
- Math Formulas
Combination Formula

The combination formula is used to find the number of ways of selecting items from a collection, such that the order of selection does not matter. In simple words, combination involves the selection of objects or things out of a larger group where order doesn’t matter.
The formula for combination helps to find the number of possible combinations that can be obtained by taking a subset of items from a larger set. It shows how many different possible subsets can be made from the larger set. It should be noted that the formula for permutation and combination are interrelated and are mentioned below.

Formula for Combination
| Combination Formula | |
| Combination Formula Using Permutation | C(n, r) = P(n,r)/ r! |
Notations in nCr Formula:
- r is the size of each permutation
- n is the size of the set from which elements are permuted
- n, r are non-negative integers
- ! is the factorial operator
The combination formula shows the number of ways a sample of “r” elements can be obtained from a larger set of “n” distinguishable objects.
Also Check: N Choose K Formula
Example Question From Combination Formula
Question 1: Father asks his son to choose 4 items from the table. If the table has 18 items to choose, how many different answers could the son give?
Solution: Given, r = 4 (item sub-set) n = 18 (larger item)
Therefore, simply: find “18 Choose 4”
= 3,060 possible answers.
Keep visiting BYJU’S to get more such maths formulas on different concepts and for different classes. Also, download the app and register now to get a more personalized and effective learning experience by getting engaging video lessons.
| FORMULAS Related Links | |

Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Request OTP on Voice Call
Post My Comment
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
mathlibra.com
Combination A combination is a selection of a group of objects, taken from a larger group for which the kinds of objects selected are important, but not the order in which they are selected.
There are several ways to find the number of possible combination. One is to use reasoning. Use the fundamental counting principle and divide by the number of ways that the object can be arranged among them. Example : Suppose we want to select two out of three boys A, B, C. Then, possible selections are AB, BC and CA.
Note: AB and BA represent the same selection.
1. All the combinations formed by a, b, c taking ab, bc, ca. 2. The only combination that can be formed of three letters a, b, c taken all at a time is abc. 3. Various groups of 2 out of four persons A, B, C, D are: AB, AC, AD, BC, BD, CD. 4. Note that ab ba are two different permutations but they represent the same combination.
Number of Combinations: The number of all combinations of n things, taken r at a time is:

Combinations Let us now assume that there is a group of 3 lawn tennis players X, Y, Z. A team consisting of 2 players is to be formed. In how many ways can we do so? Is the team of X and Y different from the team of Y and X? Here, order is not important. In fact, there are only 3 possible ways in which the team could be constructed.

Here, AB and BA are the same combination as order does not alter the combination.
This is why we have not included BA, CA, DA, CB, DB and DC in this list. There are as many as 6 combinations of 4 different objects taken 2 at a time, i.e., 4 C 2 =6. Corresponding to each combination in the list, we can arrive at 2! permutations as 2 objects in each combination can be rcarrangcd in 2! ways. Hence, the number of permutations = 4 C 2 ×2!. On the other hand, the number of permutations of 4 different things taken 2 at a time 4 P 2 . Therefore

Examples and Solutions on Combinations Example 1: In an examination in paper on advanced Accounts, 10 questions are set. In how many different ways can an examinee choose 7 questions? Solution: The number of different choices is evidently equal to the number of ways in which 7 places can be filled up by 10 different things. So the number of ways are 10 C 7 =120
Example 2: How many chords can be drawn through 21 points on a circle? Solution: For drawing one chord a circle, only 2 points are required. To know the number of chords that can be drawn through the given 21 points on a circle, the number of combinations have to be counted. Therefore, there will be as many chords as there are combinations of 21 points taken 2 at a time. Thus, required number of chords is

Example 4: In how many ways can a student choose a programme of 5 courses if 9 courses are available and 2 specific courses are compulsory for every student? Solution 4-I: There are 9 courses available out of which, 2 specific courses are compulsory for every student. Therefore, every student has to choose 3 courses out of the remaining 7 courses. This can be chosen in 7 C 3 ways. Thus, required number of ways of choosing the programme
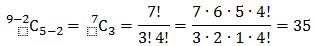
ABCDE≡BADCE≡⋯ FIG comb Hence, required number of ways is equal to
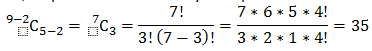
Example 8: In how many ways, 10 boys can group themselves into two teams of 5 each? A. 15120 B. 30240 C. 7560 D. None of the above correct: D, Solution: In combination be valid ‘AB’ and ‘BA’ is alike, if those are arranged of ‘A’ and ‘B’. Combination operator is made by simple pattern cases such as a case bellow.
case A: How many ways can 2 boys can be taken from 4 boys? Solution A: The respective boys are denoted by {A,B,C,D}. Entire ways of taking 2 boys are {AB,AC,AD,BC,BD,CD} Hence, the required number of ways is given by 4 C 2 =6 case B: How many ways can 4 boys divide themselves into two teams of 2 each? Solution B: The respective boys are denoted by {A,B,C,D}. Hence, the required number of ways is given by ½× 4 C 2 =3
Back to the main question. No of ways of selecting five boys = 10 C 5 . Hence the required number of ways =½× 10 C 5 =126
Example 9: In how many ways 8 boys can be distributed in two teams of 4 each to play a game of cricket? a. 2× 8 C 4 b. ½× 8 C 4 c. 8 C 4 d. 3× 8 C 4 correct: b, Solution: Four boys can be selected from 8 in 8 C 4 ways. The other 4 boys will form another team. Since, in this each group of 4 is considered twice, eg. Suppose there are 8 boys 1 to 8. One time a group will be formed from 1-4 and other time a group will be formed from 5-8. Both these groups will form same two pairs of teams. Hence, the total number of ways =½× 8 C 4 ways. Let’s read Find Difference Between Permutations and Combinations With The Best Summary
Contextual Related Posts:
- PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
- EDIT Edit this Article
- EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
- Browse Articles
- Learn Something New
- Quizzes Hot
- This Or That Game
- Train Your Brain
- Explore More
- Support wikiHow
- About wikiHow
- Log in / Sign up
- Education and Communications
- Mathematics
How to Calculate Combinations
Last Updated: April 19, 2024 References
This article was reviewed by Joseph Meyer . Joseph Meyer is a High School Math Teacher based in Pittsburgh, Pennsylvania. He is an educator at City Charter High School, where he has been teaching for over 7 years. Joseph is also the founder of Sandbox Math, an online learning community dedicated to helping students succeed in Algebra. His site is set apart by its focus on fostering genuine comprehension through step-by-step understanding (instead of just getting the correct final answer), enabling learners to identify and overcome misunderstandings and confidently take on any test they face. He received his MA in Physics from Case Western Reserve University and his BA in Physics from Baldwin Wallace University. There are 7 references cited in this article, which can be found at the bottom of the page. This article has been viewed 150,183 times.
Permutations and combinations have uses in math classes and in daily life. Thankfully, they are easy to calculate once you know how. Unlike permutations , where group order matters, in combinations, the order doesn't matter. [1] X Research source Combinations tell you how many ways there are to combine a given number of items in a group. To calculate combinations, you just need to know the number of items you're choosing from, the number of items to choose, and whether or not repetition is allowed (in the most common form of this problem, repetition is not allowed).
Calculating Combinations Without Repetition

- For instance, you may have 10 books, and you'd like to find the number of ways to combine 6 of those books on your shelf. In this case, you don't care about order - you just want to know which groupings of books you could display, assuming you only use any given book once.

- If you have a calculator available, find the factorial setting and use that to calculate the number of combinations. If you're using Google Calculator, click on the x! button each time after entering the necessary digits.
- For the example, you can calculate 10! with (10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1), which gives you 3,628,800. Find 4! with (4 * 3 * 2 * 1), which gives you 24. Find 6! with (6 * 5 * 4 * 3 * 2 * 1), which gives you 720.
- Then multiply the two numbers that add to the total of items together. In this example, you should have 24 * 720, so 17,280 will be your denominator.
- Divide the factorial of the total by the denominator, as described above: 3,628,800/17,280.
- In the example case, you'd do get 210. This means that there are 210 different ways to combine the books on a shelf, without repetition and where order doesn't matter.

To calculate the number of r-combinations from a set of n elements, we use the binomial coefficient notation C(n,r), which gives the formula C(n,r) = n! / (r!(n-r)!). This formula counts the number of ways to choose an unordered subset of r elements from a set of n elements. For example, say we want to know the number of ways to pick a committee of 5 people from a group of 12. Here, n=12 and r=5. Plugging into the formula, we get C(12,5) = 12! / (5!(12-5)!) = 792.
Calculating Combinations with Repetition
- For instance, imagine that you're going to order 5 items from a menu offering 15 items; the order of your selections doesn't matter, and you don't mind getting multiples of the same item (i.e., repetitions are allowed).

- This is the least common and least understood type of combination or permutation, and isn't generally taught as often. [9] X Research source Where it is covered, it is often also known as a k -selection, a k -multiset, or a k -combination with repetition. [10] X Research source

- If you have to solve by hand, keep in mind that for each factorial , you start with the main number given and then multiply it by the next smallest number, and so on until you get down to 0.
- For the example problem, your solution should be 11,628. There are 11,628 different ways you could order any 5 items from a selection of 15 items on a menu, where order doesn't matter and repetition is allowed.
Community Q&A
You Might Also Like

- ↑ https://www.calculatorsoup.com/calculators/discretemathematics/combinations.php
- ↑ https://betterexplained.com/articles/easy-permutations-and-combinations/
- ↑ https://www.mathsisfun.com/combinatorics/combinations-permutations.html
- ↑ https://medium.com/i-math/combinations-permutations-fa7ac680f0ac
- ↑ https://www.quora.com/What-is-Combinations-with-repetition
- ↑ https://en.wikipedia.org/wiki/Combination
- ↑ https://www.dummies.com/article/technology/electronics/graphing-calculators/permutations-and-combinations-and-the-ti-84-plus-160925/
About This Article

- Send fan mail to authors
Reader Success Stories
Nov 7, 2023
Did this article help you?

Featured Articles

Trending Articles

Watch Articles

- Terms of Use
- Privacy Policy
- Do Not Sell or Share My Info
- Not Selling Info
Get all the best how-tos!
Sign up for wikiHow's weekly email newsletter
COMBINATIONS WORD PROBLEMS EXAMPLES
Example 1 :
Kabaddi coach has 14 players ready to play. How many different teams of 7 players could the coach put on the court?
Number of ways of selecting 7 players out of 14 players
= 14 C 7
= 14! / (14 - 7)! 7!
= 14! / 7! 7!
= (14 ⋅ 13 ⋅ 12 ⋅ 11 ⋅ 10 ⋅ 9 ⋅ 8 ⋅ 7!)/7! 7!
= (14 ⋅ 13 ⋅ 12 ⋅ 11 ⋅ 10 ⋅ 9 ⋅ 8) / 7!
= (14 ⋅ 13 ⋅ 12 ⋅ 11 ⋅ 10 ⋅ 9 ⋅ 8) / (7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2)
= 3432
Example 2 :
There are 15 persons in a party and if each 2 of them shakes hands with each other, how many handshakes happen in the party?
Before going to look into the solution of this problem, let us create a model.
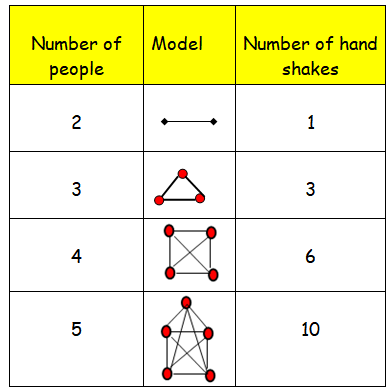
By comparing the above results, we may conclude the formula to find number of hand shakes
Number of hand shakes = n (n - 1)/2
Here we divide n (n - 1) by 2, because of avoiding repetition.
Number of persons in a party = 15
Number of hand shakes can be made = 15 (15 - 1) / 2
= 15 (14)/2
= 15 (7)
= 105
Example 3 :
How many chords can be drawn through 20 points on a circle?
20 points lie on the circle. By joining any two points on the circle, we may draw a chord.
Number of chords can be drawn = 20 C 2
= 20!/(20 - 2)! 2!
= 20! / 18! 2!
= (20 ⋅ 19) / 2
= 190
Hence the required number of chords can be drawn is 190.
Example 4 :
In a parking lot one hundred , one year old cars, are parked. Out of them five are to be chosen at random for to check its pollution devices. How many different set of five cars can be chosen?
In the given question, we have a word "different set of five cars".
So we have to use the concept combination.
Number of ways of choosing 5 cars = 100 C 5
Hence the answer is 100 C 5.
Example 5 :
How many ways can a team of 3 boys, 2 girls and 1 transgender be selected from 5 boys, 4 girls and 2 transgenders?
| Total number of boys | Number of boys to be selected | Ways |
| 5 | 3 | C = 10 |
| Total number of girls | Number of girls to be selected | Ways |
| 4 | 2 | C = 6 |
| Total number of transgenders | Number of transgenders to be selected | Ways |
| 2 | 1 | C = 2 |
Total number of ways = 10 ⋅ 6 ⋅ 2
= 120 ways
Hence the total number of ways is 120.
Kindly mail your feedback to [email protected]
We always appreciate your feedback.
© All rights reserved. onlinemath4all.com
- Sat Math Practice
- SAT Math Worksheets
- PEMDAS Rule
- BODMAS rule
- GEMDAS Order of Operations
- Math Calculators
- Transformations of Functions
- Order of rotational symmetry
- Lines of symmetry
- Compound Angles
- Quantitative Aptitude Tricks
- Trigonometric ratio table
- Word Problems
- Times Table Shortcuts
- 10th CBSE solution
- PSAT Math Preparation
- Privacy Policy
- Laws of Exponents
Recent Articles
Best way to learn mathematics.
Jul 03, 24 12:25 AM
Derivative Problems and Solutions (Part - 1)
Jun 30, 24 11:56 PM
Algebra Word Problems Involving Geometry (Video Solutions)
Jun 30, 24 01:17 PM
Combinations: Advanced Problems
- 10 C 4 = 10!/(4! × 6!) = 210
- 10 C 3 = 10!/(3! × 7!) = 120
- ( 10 C 4 ) + ( 10 C 3 ) = 210 + 120 = 330 different ways
| "; document.write(string1); document.close(); --> |
Stack Exchange Network
Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.
How would you work out these combinations?
If there are 16 different ice-cream flavours, how many combinations are there for a two scoop?
If there are still 16 different ice-cream flavours, how many combinations are there for a three scoop?
How would you work out the above combinations? I found it just sitting in my notes app and I don't recall I ever found an answer.
My thoughts at the moment are 16 * (no. of scoops) but I am still lost since of course the flavours can appear in any order. (As my SE profile will demonstrate, I'm not much of a mathematician!)
So what would an equation be for the following as applicable to both Problem 1 and Problem 2?
A. Working out the number of combinations including duplicate scoops (e.g. chocolate-chocolate-vanilla)
B. Working out the number of combinations where a flavour only appears once in each possible combination (e.g. chocolate-vanilla-strawberry and then vanilla-chocolate-strawberry).
Any help would be much appreciated!
- combinations
- problem-solving
2 Answers 2
1: This problem is equivalent to putting two identical balls into 16 boxes (with repetition allowed). $\binom{2+16-1}{2}$
Where 2 is the number of balls, and $16-1$ is the number of separators needed to divided a line segment into 16 smaller segments,each segment represents a box.
Each way of putting the balls (each combination of flavors) will be corresponds to a arrangement of $2$ balls and $16-1$ seperators (where balls and seperators are indistinguishable among themselves).
2.$\binom{3+16-1}{3}$.
A. As shown above, where we assume repetition is allowed.
B. If repetition is not allow,
$\binom{16}{2}$
$\binom{16}{3}$
1) working out the number of combinations including duplicate scoops (e.g. chocolate-chocolate-vanilla)
Consider the case where there is only one scoop of ice cream. There are 16 flavors (choices), and thus 16 "combinations." The next case is 2 scoops. One way to think about this problem is to consider how many choices you have per scoop. There are 16 choices for the first scoop and 16 choices for the second scoop since duplicates are allowed. This works out to $16^2 = 256$. It should be more clear as to how you can expand this to more scoops.
2) working out the number of combinations where a flavour only appears once in each possible combination (e.g. chocolate-vanilla-strawberry and then vanilla-chocolate-strawberry)
Now try the case of 3 scoops. There are 16 choices for the first scoop, but 15 choices for the second scoop since duplicates are not allowed. For the third scoop there are 14 choices, which works out to $16*15*14=3,360$. Note that with this way of combining flavors, the order is important since chocolate-vanilla-strawberry and vanilla-chocolate-strawberry are both counted.
EDIT (for cases where duplicates are allowed):
1.If there are 16 different ice-cream flavours, how many combinations are there for a two scoop?
There's a decent explanation from another post . The formula is indeed $$ \binom{n+k-1}{k} $$
where $n$ is the number of flavors and $k$ is the number of scoops. This is called a combination . Note that using this formula gives a different answer than I originally provided, since combinations do not consider the order in which objects are counted $$ \binom{16+2-1}{2}=\binom {17}2=\frac{17\cdot16}{1\cdot2}=136 $$
Using the formula above it can be worked out similarly $$ \binom{16+3-1}{3}=\binom {18}3=\frac{18\cdot17\cdot16}{1\cdot2\cdot3}=816 $$
- $\begingroup$ Thank you. Though I mustn't have been as clear as possible. 1) and 2) do not correlate to the first and second predicaments; they are meant as sub points for each problem if that makes sense. I have edited the question to reflect this. $\endgroup$ – Dog Lover Commented Jul 13, 2016 at 2:26
- $\begingroup$ Would you be able to edit your answer accordingly, as so far your answer is excellent. $\endgroup$ – Dog Lover Commented Jul 13, 2016 at 2:32
- $\begingroup$ @DogLover I added a little more to my answer including the more likely formula that you're looking for. I know I'm not as comprehensive as I could be, but I hope this helps your intuition as to how this problem is worked out. $\endgroup$ – Jonathan So Commented Jul 13, 2016 at 3:01
- $\begingroup$ Thank you! Just what I was after, plus I learnt something new: mathematical combinations. Although is there a reason why 1 is subtracted from the number of scoops? Is it something to do with zero-indexing? $\endgroup$ – Dog Lover Commented Jul 13, 2016 at 3:10
- $\begingroup$ @DogLover You're welcome! Glad I could help. And to answer your question, kind of. This problem is very related to what is known as the Stars and Bars technique. A little bit of it was shown in the post I linked, and a more detailed description and usage can be found here . Without additional reading I can't honestly say I remember why 1 is subtracted, but in stars and bars there will always be 1 less bar separating the $k$ objects. $\endgroup$ – Jonathan So Commented Jul 13, 2016 at 3:17
You must log in to answer this question.
Not the answer you're looking for browse other questions tagged combinations problem-solving ..
- Featured on Meta
- We spent a sprint addressing your requests — here’s how it went
- Upcoming initiatives on Stack Overflow and across the Stack Exchange network...
Hot Network Questions
- Why are 16th note apoggiaturas not written as normal 16th notes?
- Greek myth about an athlete who kills another man with a discus
- When do you know things are actually going poorly in graduate school?
- Do thermodynamic cycles occur only in human-made machines?
- As an advisor, how can I help students with time management and procrastination?
- GDPR Data Processor
- Pregnancy in a hibernated state
- Don't make noise. OR Don't make a noise
- Concrete works by Alexandre Grothendieck, other than Dessin d'Enfants?
- Beer clip packaging
- Did any attendees write up accounts of pre-1980 Homebrew Computer Club meetings?
- How does the temperature of the condenser impact an air conditioner's energy usage?
- How well does the following argument work as a counter towards unfalsifiable supernatural claims?
- Old SF story about someone who detonated an atomic bomb, sacrificing self to save society from an evil government
- Sitting on a desk or at a desk? What's the diffrence?
- Where is the pentagon in the Fibonacci sequence?
- Why does Paul's fight with Feyd-Rautha take so long?
- Why does the Trump immunity decision further delay the trial?
- Measure by mass vs. 'Spooned and Leveled'
- Are US enlisted personnel (as opposed to officers) required, or allowed, to disobey unlawful orders?
- In-Place Reordering of Doubly Linked List Nodes to Ensure Memory Contiguity
- Align 3 tables neatly
- How do I drill a 60cm hole in a tree stump, 4.4 cm wide?
- What is the translation of "a discrete GPU" in French?
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Statistics and probability
Course: statistics and probability > unit 8.
- Probability using combinations
- Probability & combinations (2 of 2)
- Example: Different ways to pick officers
Example: Combinatorics and probability
- Getting exactly two heads (combinatorics)
- Exactly three heads in five flips
- Generalizing with binomial coefficients (bit advanced)
- Example: Lottery probability
- Probability with permutations and combinations
- Conditional probability and combinations
- Mega millions jackpot probability
- Birthday probability problem
Want to join the conversation?
- Upvote Button navigates to signup page
- Downvote Button navigates to signup page
- Flag Button navigates to signup page

Video transcript
The McKinsey Crossword: In the Zone | No. 187
Play the interactive version, or if you like putting pen(cil) to paper, download and print when you're ready to engage. Check back each Tuesday for a new puzzle or, better yet, sign up to get an alert each week when the next challenge is ready.
See all puzzles
Related Articles

The case for space

The state of AI in early 2024: Gen AI adoption spikes and starts to generate value

COMMENTS
Find the number of strings of 4 letters that can be formed with the letters of the word EXAMINATION? Solution : There are 11 letters not all different. They are AA, II, NN, E, X, M, T, O. The following combinations are possible: Case 1 : Number of ways selecting 2 alike, 2 alike. = 3C2 = 3 ways. Case 2 :
Combination questions with solutions are given here to practice and to understand how and when to use the concept of combinations while solving a problem. Also, try important permutation and combination questions for class 11. In combinatorics, the combination is a way of selecting something from a given collection. For example, we have to form ...
Examples of solving Combination Problems with videos and solutions, Formula to find the number of combinations of n things taken r at a time, What is the Combination Formula, How to use the Combination Formula to solve word problems and counting problems, How to solve combination problems that involve selecting groups based on conditional criteria, How to solve word problems involving ...
Combinations. When a customer buys a family-sized meal at certain restaurant, they get to choose 3 side dishes from 9 options. Suppose a customer is going to choose 3 different side dishes. How many groups of 3 different side dishes are possible? Learn for free about math, art, computer programming, economics, physics, chemistry, biology ...
7. On a graduation party the graduants pinged their glasses. There were 253 pings. How many graduants came to the party? Solution: There were 23 graduants on the party. 8. If the number of elements would raise by 8, number of combinations with k=2 without repetition would raise 11 times.
A combination is a way of choosing elements from a set in which order does not matter. A wide variety of counting problems can be cast in terms of the simple concept of combinations, therefore, this topic serves as a building block in solving a wide range of problems. Introduction. Basic Examples. Intermediate Examples.
A permutation is an arrangement in a definite order of a number of objects taken, some or all at a time. The combination is a way of selecting items from a collection, such that (unlike permutations) the order of selection does not matter. Also, read: Permutation and combination. Permutations and Combinations Questions and Answers. 1.
10,000 combinations. First method: If you count from 0001 to 9999, that's 9999 numbers. Then you add 0000, which makes it 10,000. Second method: 4 digits means each digit can contain 0-9 (10 combinations). The first digit has 10 combinations, the second 10, the third 10, the fourth 10. So 10*10*10*10=10,000.
Permutations & combinations. You need to put your reindeer, Prancer, Quentin, Rudy, and Jebediah, in a single-file line to pull your sleigh. However, Rudy and Prancer are best friends, so you have to put them next to each other, or they won't fly. How many ways can you arrange your reindeer? Learn for free about math, art, computer programming ...
Summary of combinations. Combinations are selections of objects in a collection, in which the order of the selection does not matter. In combinations, we can select the objects in any order. For example, if we have ab and ba, these selections are considered equal in combinations. The formula to determine the number of possible organizations by ...
These permutations and combinations worksheets consist of an array of exercises to identify and write permutations / combinations, twin-level of solving equations and evaluating expressions. Access our combination worksheets feature topics like listing out the number of combinations, evaluate and solve the combination problems and more.
Problem 3 : Determine the number of 5 card combinations out of a deck of 52 cards if there is exactly three aces in each combination. Solution : Total number of cards in a deck = 52. Number of ace cards = 4. Number of cards to be selected = 5. Here we must select 3 ace cards out of 4 and 2 other cards out of 48. Number of ways :
Combinations. There are also two types of combinations (remember the order does not matter now): Repetition is Allowed: such as coins in your pocket (5,5,5,10,10) No Repetition: such as lottery numbers (2,14,15,27,30,33) 1. Combinations with Repetition. Actually, these are the hardest to explain, so we will come back to this later. 2.
A series of college algebra lectures: Solving Problems Involving Permutations, Solving Problems Involving Combinations, Independent Events, Inclusive Events. Solving Problems Involving Permutations. Examples: A museum has 7 paintings by Picasso and wants to arrange 3 of them on the same wall.
Example Question From Combination Formula. Question 1: Father asks his son to choose 4 items from the table. If the table has 18 items to choose, how many different answers could the son give? Therefore, simply: find "18 Choose 4". We know that, Combination = C (n, r) = n!/r! (n-r)!
These examples suggest the following theorem showing relationship between permutaion and combination: n P r = n C r ×r!,0≤r≤n Proof Corresponding to each combination of n C r we have r! permutations, because r objects in every combination can be rearranged in r! ways. Hence, the total number of permutations of n different things taken r at a time is n C r ×r!. ...
Find 6! with (6 * 5 * 4 * 3 * 2 * 1), which gives you 720. Then multiply the two numbers that add to the total of items together. In this example, you should have 24 * 720, so 17,280 will be your denominator. Divide the factorial of the total by the denominator, as described above: 3,628,800/17,280.
So we have to use the concept combination. Number of ways of choosing 5 cars = 100 C 5. Hence the answer is 100 C 5. Example 5 : How many ways can a team of 3 boys, 2 girls and 1 transgender be selected from 5 boys, 4 girls and 2 transgenders? Solution :
These combination problems are sometimes called 'less than' problems. ... Problem 1) There are eight candidates at school running for three seats in the student government. If you can vote for three or few students. ... In how many different ways can you vote? Answer 8 C 3 + 8 C 2 + 8 C 1 =56 +28 +8 = 92 . Problem 2) Fourteen students want to ...
Probability & combinations (2 of 2) Example: Different ways to pick officers. Example: Combinatorics and probability. Getting exactly two heads (combinatorics) Exactly three heads in five flips. Generalizing with binomial coefficients (bit advanced) Example: Lottery probability. Conditional probability and combinations.
‼️THIRD QUARTER‼️🔵 GRADE 10: SOLVING WORD PROBLEMS INVOLVING PERMUTATIONS AND COMBINATIONS 🔵 GRADE 10 PLAYLISTFirst Quarter: https://tinyurl.com ...
1. 1) working out the number of combinations including duplicate scoops (e.g. chocolate-chocolate-vanilla) Consider the case where there is only one scoop of ice cream. There are 16 flavors (choices), and thus 16 "combinations." The next case is 2 scoops. One way to think about this problem is to consider how many choices you have per scoop.
The probability of drawing the 2nd one is 3/35. 3. The probability of drawing the 3rd one is 2/34. 4. The probability of drawing the 4th one is 1/33. Multiplying these 4 numbers together and then multiplying this result with (9 choose 4), which is 126 will give you 2/935 , the same number Sal got.
Sharpen your problem-solving skills the McKinsey way, with our weekly crossword. Each puzzle is created with the McKinsey audience in mind, and includes a subtle (and sometimes not-so-subtle) business theme for you to find. Answers that are directionally correct may not cut it if you're looking for a quick win.