The JASP guidelines for conducting and reporting a Bayesian analysis
- Theoretical Review
- Open access
- Published: 09 October 2020
- Volume 28 , pages 813–826, ( 2021 )

Cite this article
You have full access to this open access article

- Johnny van Doorn 1 ,
- Don van den Bergh 1 ,
- Udo Böhm 1 ,
- Fabian Dablander 1 ,
- Koen Derks 2 ,
- Tim Draws 1 ,
- Alexander Etz 3 ,
- Nathan J. Evans 1 ,
- Quentin F. Gronau 1 ,
- Julia M. Haaf 1 ,
- Max Hinne 1 ,
- Šimon Kucharský 1 ,
- Alexander Ly 1 , 4 ,
- Maarten Marsman 1 ,
- Dora Matzke 1 ,
- Akash R. Komarlu Narendra Gupta 1 ,
- Alexandra Sarafoglou 1 ,
- Angelika Stefan 1 ,
- Jan G. Voelkel 5 &
- Eric-Jan Wagenmakers 1
40k Accesses
450 Citations
44 Altmetric
Explore all metrics
Despite the increasing popularity of Bayesian inference in empirical research, few practical guidelines provide detailed recommendations for how to apply Bayesian procedures and interpret the results. Here we offer specific guidelines for four different stages of Bayesian statistical reasoning in a research setting: planning the analysis, executing the analysis, interpreting the results, and reporting the results. The guidelines for each stage are illustrated with a running example. Although the guidelines are geared towards analyses performed with the open-source statistical software JASP, most guidelines extend to Bayesian inference in general.
Similar content being viewed by others
Bayesian Analysis Reporting Guidelines
Four reasons to prefer bayesian analyses over significance testing, how to become a bayesian in eight easy steps: an annotated reading list.
Avoid common mistakes on your manuscript.
In recent years, Bayesian inference has become increasingly popular, both in statistical science and in applied fields such as psychology, biology, and econometrics (e.g., Andrews & Baguley, 2013 ; Vandekerckhove, Rouder, & Kruschke, 2018 ). For the pragmatic researcher, the adoption of the Bayesian framework brings several advantages over the standard framework of frequentist null-hypothesis significance testing (NHST), including (1) the ability to obtain evidence in favor of the null hypothesis and discriminate between “absence of evidence” and “evidence of absence” (Dienes, 2014 ; Keysers, Gazzola, & Wagenmakers, 2020 ); (2) the ability to take into account prior knowledge to construct a more informative test (Gronau, Ly, & Wagenmakers, 2020 ; Lee & Vanpaemel, 2018 ); and (3) the ability to monitor the evidence as the data accumulate (Rouder, 2014 ). However, the relative novelty of conducting Bayesian analyses in applied fields means that there are no detailed reporting standards, and this in turn may frustrate the broader adoption and proper interpretation of the Bayesian framework.
Several recent statistical guidelines include information on Bayesian inference, but these guidelines are either minimalist (Appelbaum et al., 2018 ; The BaSiS group, 2001 ), focus only on relatively complex statistical tests (Depaoli & Schoot, 2017 ), are too specific to a certain field (Spiegelhalter, Myles, Jones, & Abrams, 2000 ; Sung et al., 2005 ), or do not cover the full inferential process (Jarosz & Wiley, 2014 ). The current article aims to provide a general overview of the different stages of the Bayesian reasoning process in a research setting. Specifically, we focus on guidelines for analyses conducted in JASP (JASP Team, 2019 ; jasp-stats.org ), although these guidelines can be generalized to other software packages for Bayesian inference. JASP is an open-source statistical software program with a graphical user interface that features both Bayesian and frequentist versions of common tools such as the t test, the ANOVA, and regression analysis (e.g., Marsman & Wagenmakers, 2017 ; Wagenmakers et al., 2018 ).
We discuss four stages of analysis: planning, executing, interpreting, and reporting. These stages and their individual components are summarized in Table 1 . In order to provide a concrete illustration of the guidelines for each of the four stages, each section features a data set reported by Frisby and Clatworthy ( 1975 ). This data set concerns the time it took two groups of participants to see a figure hidden in a stereogram—one group received advance visual information about the scene (i.e., the VV condition), whereas the other group did not (i.e., the NV condition). Footnote 1 Three additional examples (mixed ANOVA, correlation analysis, and a t test with an informed prior) are provided in an online appendix at https://osf.io/nw49j/ . Throughout the paper, we present three boxes that provide additional technical discussion. These boxes, while not strictly necessary, may prove useful to readers interested in greater detail.
Stage 1: Planning the analysis
Specifying the goal of the analysis..
We recommend that researchers carefully consider their goal, that is, the research question that they wish to answer, prior to the study (Jeffreys, 1939 ). When the goal is to ascertain the presence or absence of an effect, we recommend a Bayes factor hypothesis test (see Box 1). The Bayes factor compares the predictive performance of two hypotheses. This underscores an important point: in the Bayes factor testing framework, hypotheses cannot be evaluated until they are embedded in fully specified models with a prior distribution and likelihood (i.e., in such a way that they make quantitative predictions about the data). Thus, when we refer to the predictive performance of a hypothesis, we implicitly refer to the accuracy of the predictions made by the model that encompasses the hypothesis (Etz, Haaf, Rouder, & Vandekerckhove, 2018 ).
When the goal is to determine the size of the effect, under the assumption that it is present, we recommend to plot the posterior distribution or summarize it by a credible interval (see Box 2). Testing and estimation are not mutually exclusive and may be used in sequence; for instance, one may first use a test to ascertain that the effect exists, and then continue to estimate the size of the effect.
Box 1. Hypothesis testing
The principled approach to Bayesian hypothesis testing is by means of the Bayes factor (e.g., Etz & Wagenmakers, 2017 ; Jeffreys, 1939 ; Ly, Verhagen, & Wagenmakers, 2016 ; Wrinch & Jeffreys, 1921 ). The Bayes factor quantifies the relative predictive performance of two rival hypotheses, and it is the degree to which the data demand a change in beliefs concerning the hypotheses’ relative plausibility (see Equation 1 ). Specifically, the first term in Equation 1 corresponds to the prior odds, that is, the relative plausibility of the rival hypotheses before seeing the data. The second term, the Bayes factor, indicates the evidence provided by the data. The third term, the posterior odds, indicates the relative plausibility of the rival hypotheses after having seen the data.
The subscript in the Bayes factor notation indicates which hypothesis is supported by the data. BF 10 indicates the Bayes factor in favor of \({\mathscr{H}}_{1}\) over \({\mathscr{H}}_{0}\) , whereas BF 01 indicates the Bayes factor in favor of \({\mathscr{H}}_{0}\) over \({\mathscr{H}}_{1}\) . Specifically, BF 10 = 1/BF 01 . Larger values of BF 10 indicate more support for \({\mathscr{H}}_{1}\) . Bayes factors range from 0 to \(\infty \) , and a Bayes factor of 1 indicates that both hypotheses predicted the data equally well. This principle is further illustrated in Figure 4 .
Box 2. Parameter estimation
For Bayesian parameter estimation, interest centers on the posterior distribution of the model parameters. The posterior distribution reflects the relative plausibility of the parameter values after prior knowledge has been updated by means of the data. Specifically, we start the estimation procedure by assigning the model parameters a prior distribution that reflects the relative plausibility of each parameter value before seeing the data. The information in the data is then used to update the prior distribution to the posterior distribution. Parameter values that predicted the data relatively well receive a boost in plausibility, whereas parameter values that predicted the data relatively poorly suffer a decline (Wagenmakers, Morey, & Lee, 2016 ). Equation 2 illustrates this principle. The first term indicates the prior beliefs about the values of parameter 𝜃 . The second term is the updating factor: for each value of 𝜃 , the quality of its prediction is compared to the average quality of the predictions over all values of 𝜃 . The third term indicates the posterior beliefs about 𝜃 .
The posterior distribution can be plotted or summarized by an x % credible interval. An x % credible interval contains x % of the posterior mass. Two popular ways of creating a credible interval are the highest density credible interval, which is the narrowest interval containing the specified mass, and the central credible interval, which is created by cutting off \(\frac {100-x}{2}\%\) from each of the tails of the posterior distribution.
Specifying the statistical model.
The functional form of the model (i.e., the likelihood; Etz, 2018 ) is guided by the nature of the data and the research question. For instance, if interest centers on the association between two variables, one may specify a bivariate normal model in order to conduct inference on Pearson’s correlation parameter ρ . The statistical model also determines which assumptions ought to be satisfied by the data. For instance, the statistical model might assume the dependent variable to be normally distributed. Violations of assumptions may be addressed at different points in the analysis, such as the data preprocessing steps discussed below, or by planning to conduct robust inferential procedures as a contingency plan.
The next step in model specification is to determine the sidedness of the procedure. For hypothesis testing, this means deciding whether the procedure is one-sided (i.e., the alternative hypothesis dictates a specific direction of the population effect) or two-sided (i.e., the alternative hypothesis dictates that the effect can be either positive or negative). The choice of one-sided versus two-sided depends on the research question at hand and this choice should be theoretically justified prior to the study. For hypothesis testing it is usually the case that the alternative hypothesis posits a specific direction. In Bayesian hypothesis testing, a one-sided hypothesis yields a more diagnostic test than a two-sided alternative (e.g., Jeffreys, 1961 ; Wetzels, Raaijmakers, Jakab, & Wagenmakers, 2009 , p.283). Footnote 2
For parameter estimation, we recommend to always use the two-sided model instead of the one-sided model: when a positive one-sided model is specified but the observed effect turns out to be negative, all of the posterior mass will nevertheless remain on the positive values, falsely suggesting the presence of a small positive effect.
The next step in model specification concerns the type and spread of the prior distribution, including its justification. For the most common statistical models (e.g., correlations, t tests, and ANOVA), certain “default” prior distributions are available that can be used in cases where prior knowledge is absent, vague, or difficult to elicit (for more information, see Ly et al.,, 2016 ). These priors are default options in JASP. In cases where prior information is present, different “informed” prior distributions may be specified. However, the more the informed priors deviate from the default priors, the stronger becomes the need for a justification (see the informed t test example in the online appendix at https://osf.io/ybszx/ ). Additionally, the robustness of the result to different prior distributions can be explored and included in the report. This is an important type of robustness check because the choice of prior can sometimes impact our inferences, such as in experiments with small sample sizes or missing data. In JASP, Bayes factor robustness plots show the Bayes factor for a wide range of prior distributions, allowing researchers to quickly examine the extent to which their conclusions depend on their prior specification. An example of such a plot is given later in Figure 7 .
Specifying data preprocessing steps.
Dependent on the goal of the analysis and the statistical model, different data preprocessing steps might be taken. For instance, if the statistical model assumes normally distributed data, a transformation to normality (e.g., the logarithmic transformation) might be considered (e.g., Draper & Cox, 1969 ). Other points to consider at this stage are when and how outliers may be identified and accounted for, which variables are to be analyzed, and whether further transformation or combination of data are necessary. These decisions can be somewhat arbitrary, and yet may exert a large influence on the results (Wicherts et al., 2016 ). In order to assess the degree to which the conclusions are robust to arbitrary modeling decisions, it is advisable to conduct a multiverse analysis (Steegen, Tuerlinckx, Gelman, & Vanpaemel, 2016 ). Preferably, the multiverse analysis is specified at study onset. A multiverse analysis can easily be conducted in JASP, but doing so is not the goal of the current paper.
Specifying the sampling plan.
As may be expected from a framework for the continual updating of knowledge, Bayesian inference allows researchers to monitor evidence as the data come in, and stop whenever they like, for any reason whatsoever. Thus, strictly speaking there is no Bayesian need to pre-specify sample size at all (e.g., Berger & Wolpert, 1988 ). Nevertheless, Bayesians are free to specify a sampling plan if they so desire; for instance, one may commit to stop data collection as soon as BF 10 ≥ 10 or BF 01 ≥ 10. This approach can also be combined with a maximum sample size ( N ), where data collection stops when either the maximum N or the desired Bayes factor is obtained, whichever comes first (for examples see ; Matzke et al., 2015 ;Wagenmakers et al., 2015 ).
In order to examine what sampling plans are feasible, researchers can conduct a Bayes factor design analysis (Schönbrodt & Wagenmakers, 2018 ; Stefan, Gronau, Schönbrodt, & Wagenmakers, 2019 ), a method that shows the predicted outcomes for different designs and sampling plans. Of course, when the study is observational and the data are available ‘en bloc’, the sampling plan becomes irrelevant in the planning stage.
Stereogram example
First, we consider the research goal, which was to determine if participants who receive advance visual information exhibit a shorter fuse time (Frisby & Clatworthy, 1975 ). A Bayes factor hypothesis test can be used to quantify the evidence that the data provide for and against the hypothesis that an effect is present. Should this test reveal support in favor of the presence of the effect, then we have grounds for a follow-up analysis in which the size of the effect is estimated.
Second, we specify the statistical model. The study focus is on the difference in performance between two between-subjects conditions, suggesting a two-sample t test on the fuse times is appropriate. The main measure of the study is a reaction time variable, which can for various reasons be non-normally distributed (Lo & Andrews, 2015 ; but see Schramm & Rouder, 2019 ). If our data show signs of non-normality we will conduct two alternatives: a t test on the log-transformed fuse time data and a non-parametric t test (i.e., the Mann–Whitney U test), which is robust to non-normality and unaffected by the log-transformation of the fuse times.
For hypothesis testing, we compare the null hypothesis (i.e., advance visual information has no effect on fuse times) to a one-sided alternative hypothesis (i.e., advance visual information shortens the fuse times), in line with the directional nature of the original research question. The rival hypotheses are thus \({\mathscr{H}}_{0}: \delta = 0\) and \({\mathscr{H}}_{+}: \delta > 0\) , where δ is the standardized effect size (i.e., the population version of Cohen’s d ), \({\mathscr{H}}_{0}\) denotes the null hypothesis, and \({\mathscr{H}}_{+}\) denotes the one-sided alternative hypothesis (note the ‘+’ in the subscript). For parameter estimation (under the assumption that the effect exists), we use the two-sided t test model and plot the posterior distribution of δ . This distribution can also be summarized by a 95 % central credible interval.
We complete the model specification by assigning prior distributions to the model parameters. Since we have only little prior knowledge about the topic, we select a default prior option for the two-sample t test, that is, a Cauchy distribution Footnote 3 with spread r set to \({1}/{\sqrt {2}}\) . Since we specified a one-sided alternative hypothesis, the prior distribution is truncated at zero, such that only positive effect size values are allowed. The robustness of the Bayes factor to this prior specification can be easily assessed in JASP by means of a Bayes factor robustness plot.
Since the data are already available, we do not have to specify a sampling plan. The original data set has a total sample size of 103, from which 25 participants were eliminated due to failing an initial stereo-acuity test, leaving 78 participants (43 in the NV condition and 35 in the VV condition). The data are available online at https://osf.io/5vjyt/ .
Stage 2: Executing the analysis
Before executing the primary analysis and interpreting the outcome, it is important to confirm that the intended analyses are appropriate and the models are not grossly misspecified for the data at hand. In other words, it is strongly recommended to examine the validity of the model assumptions (e.g., normally distributed residuals or equal variances across groups). Such assumptions may be checked by plotting the data, inspecting summary statistics, or conducting formal assumption tests (but see Tijmstra, 2018 ).
A powerful demonstration of the dangers of failing to check the assumptions is provided by Anscombe’s quartet (Anscombe, 1973 ; see Fig. 1 ). The quartet consists of four fictitious data sets of equal size that each have the same observed Pearson’s product moment correlation r , and therefore lead to the same inferential result both in a frequentist and a Bayesian framework. However, visual inspection of the scatterplots immediately reveals that three of the four data sets are not suitable for a linear correlation analysis, and the statistical inference for these three data sets is meaningless or even misleading. This example highlights the adage that conducting a Bayesian analysis does not safeguard against general statistical malpractice—the Bayesian framework is as vulnerable to violations of assumptions as its frequentist counterpart. In cases where assumptions are violated, an ordinal or non-parametric test can be used, and the parametric results should be interpreted with caution.
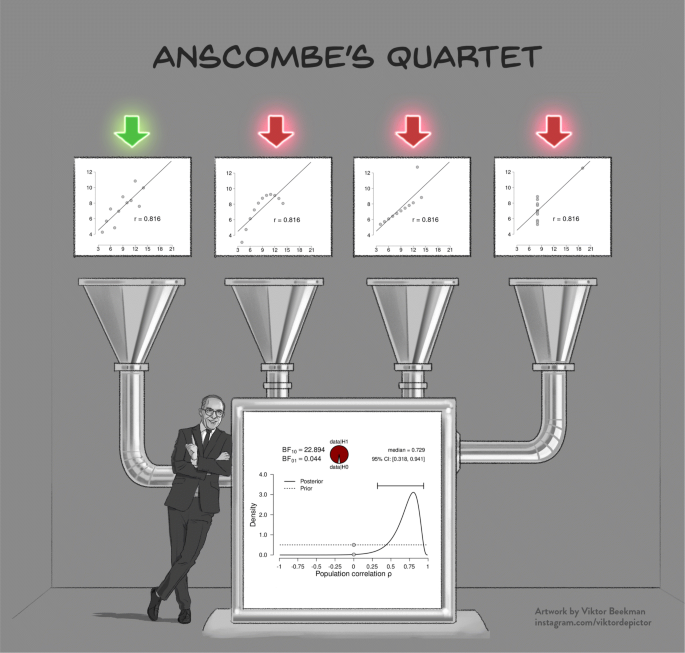
Model misspecification is also a problem for Bayesian analyses. The four scatterplots in the top panel show Anscombe’s quartet (Anscombe, 1973 ); the bottom panel shows the corresponding inference, which is identical for all four scatter plots. Except for the leftmost scatterplot, all data violate the assumptions of the linear correlation analysis in important ways
Once the quality of the data has been confirmed, the planned analyses can be carried out. JASP offers a graphical user interface for both frequentist and Bayesian analyses. JASP 0.10.2 features the following Bayesian analyses: the binomial test, the Chi-square test, the multinomial test, the t test (one-sample, paired sample, two-sample, Wilcoxon rank-sum, and Wilcoxon signed-rank tests), A/B tests, ANOVA, ANCOVA, repeated measures ANOVA, correlations (Pearson’s ρ and Kendall’s τ ), linear regression, and log-linear regression. After loading the data into JASP, the desired analysis can be conducted by dragging and dropping variables into the appropriate boxes; tick marks can be used to select the desired output.
The resulting output (i.e., figures and tables) can be annotated and saved as a .jasp file. Output can then be shared with peers, with or without the real data in the .jasp file; if the real data are added, reviewers can easily reproduce the analyses, conduct alternative analyses, or insert comments.
In order to check for violations of the assumptions of the t test, the top row of Fig. 2 shows boxplots and Q-Q plots of the dependent variable fuse time, split by condition. Visual inspection of the boxplots suggests that the variances of the fuse times may not be equal (observed standard deviations of the NV and VV groups are 8.085 and 4.802, respectively), suggesting the equal variance assumption may be unlikely to hold. There also appear to be a number of potential outliers in both groups. Moreover, the Q-Q plots show that the normality assumption of the t test is untenable here. Thus, in line with our analysis plan we will apply the log-transformation to the fuse times. The standard deviations of the log-transformed fuse times in the groups are roughly equal (observed standard deviations are 0.814 and 0.818 in the NV and the VV group, respectively); the Q-Q plots in the bottom row of Fig. 2 also look acceptable for both groups and there are no apparent outliers. However, it seems prudent to assess the robustness of the result by also conducting the Bayesian Mann–Whitney U test (van Doorn, Ly, Marsman, & Wagenmakers, 2020 ) on the fuse times.
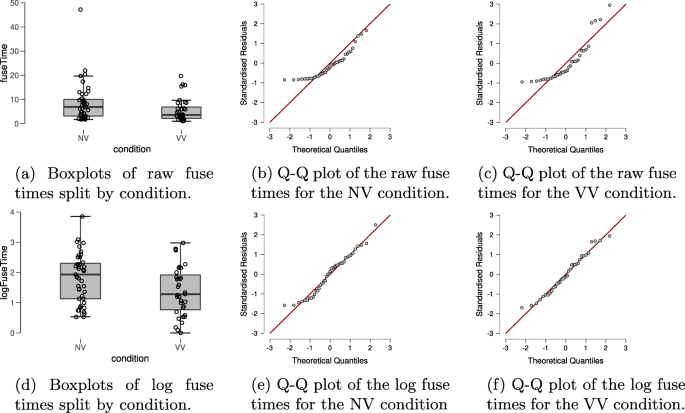
Descriptive plots allow a visual assessment of the assumptions of the t test for the stereogram data. The top row shows descriptive plots for the raw fuse times, and the bottom row shows descriptive plots for the log-transformed fuse times. The left column shows boxplots, including the jittered data points, for each of the experimental conditions. The middle and right columns show parQ-Q plots of the dependent variable, split by experimental condition. Here we see that the log-transformed dependent variable is more appropriate for the t test, due to its distribution and absence of outliers. Figures from JASP
Following the assumption check, we proceed to execute the analyses in JASP. For hypothesis testing, we obtain a Bayes factor using the one-sided Bayesian two-sample t test. Figure 3 shows the JASP user interface for this procedure. For parameter estimation, we obtain a posterior distribution and credible interval, using the two-sided Bayesian two-sample t test. The relevant boxes for the various plots were ticked, and an annotated .jasp file was created with all of the relevant analyses: the one-sided Bayes factor hypothesis tests, the robustness check, the posterior distribution from the two-sided analysis, and the one-sided results of the Bayesian Mann–Whitney U test. The .jasp file can be found at https://osf.io/nw49j/ . The next section outlines how these results are to be interpreted.
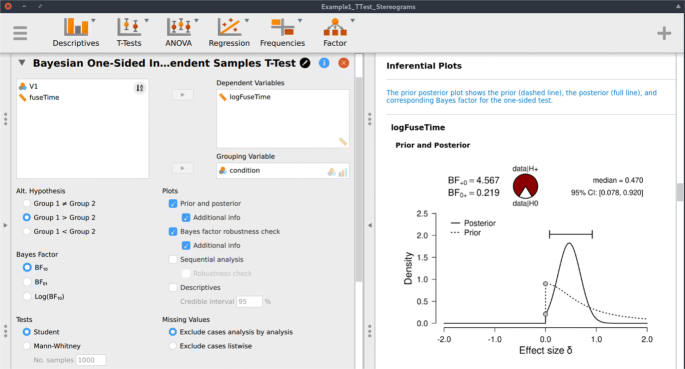
JASP menu for the Bayesian two-sample t test. The left input panel offers the analysis options, including the specification of the alternative hypothesis and the selection of plots. The right output panel shows the corresponding analysis output. The prior and posterior plot is explained in more detail in Fig. 6 . The input panel specifies the one-sided analysis for hypothesis testing; a two-sided analysis for estimation can be obtained by selecting “Group 1 ≠ Group 2” under “Alt. Hypothesis”
Stage 3: Interpreting the results
With the analysis outcome in hand, we are ready to draw conclusions. We first discuss the scenario of hypothesis testing, where the goal typically is to conclude whether an effect is present or absent. Then, we discuss the scenario of parameter estimation, where the goal is to estimate the size of the population effect, assuming it is present. When both hypothesis testing and estimation procedures have been planned and executed, there is no predetermined order for their interpretation. One may adhere to the adage “only estimate something when there is something to be estimated” (Wagenmakers et al., 2018 ) and first test whether an effect is present, and then estimate its size (assuming the test provided sufficiently strong evidence against the null), or one may first estimate the magnitude of an effect, and then quantify the degree to which this magnitude warrants a shift in plausibility away from or toward the null hypothesis (but see Box 3).
If the goal of the analysis is hypothesis testing, we recommend using the Bayes factor. As described in Box 1, the Bayes factor quantifies the relative predictive performance of two rival hypotheses (Wagenmakers et al., 2016 ; see Box 1). Importantly, the Bayes factor is a relative metric of the hypotheses’ predictive quality. For instance, if BF 10 = 5, this means that the data are 5 times more likely under \({\mathscr{H}}_{1}\) than under \({\mathscr{H}}_{0}\) . However, a Bayes factor in favor of \({\mathscr{H}}_{1}\) does not mean that \({\mathscr{H}}_{1}\) predicts the data well. As Figure 1 illustrates, \({\mathscr{H}}_{1}\) provides a dreadful account of three out of four data sets, yet is still supported relative to \({\mathscr{H}}_{0}\) .
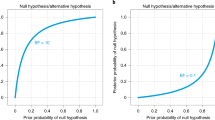
There can be no hard Bayes factor bound (other than zero and infinity) for accepting or rejecting a hypothesis wholesale, but there have been some attempts to classify the strength of evidence that different Bayes factors provide (e.g., Jeffreys, 1939 ; Kass & Raftery, 1995 ). One such classification scheme is shown in Figure 4 . Several magnitudes of the Bayes factor are visualized as a probability wheel, where the proportion of red to white is determined by the degree of evidence in favor of \({\mathscr{H}}_{0}\) and \({\mathscr{H}}_{1}\) . Footnote 4 In line with Jeffreys, a Bayes factor between 1 and 3 is considered weak evidence, a Bayes factor between 3 and 10 is considered moderate evidence, and a Bayes factor greater than 10 is considered strong evidence. Note that these classifications should only be used as general rules of thumb to facilitate communication and interpretation of evidential strength. Indeed, one of the merits of the Bayes factor is that it offers an assessment of evidence on a continuous scale.
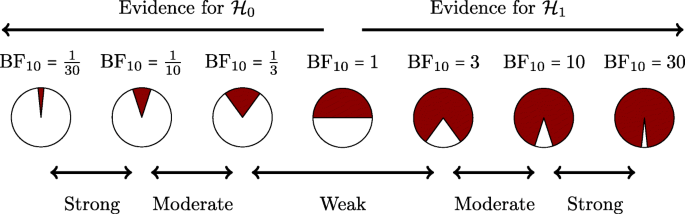
A graphical representation of a Bayes factor classification table. As the Bayes factor deviates from 1, which indicates equal support for \({\mathscr{H}}_{0}\) and \({\mathscr{H}}_{1}\) , more support is gained for either \({\mathscr{H}}_{0}\) or \({\mathscr{H}}_{1}\) . Bayes factors between 1 and 3 are considered to be weak, Bayes factors between 3 and 10 are considered moderate, and Bayes factors greater than 10 are considered strong evidence. The Bayes factors are also represented as probability wheels, where the ratio of white (i.e., support for \({\mathscr{H}}_{0}\) ) to red (i.e., support for \({\mathscr{H}}_{1}\) ) surface is a function of the Bayes factor. The probability wheels further underscore the continuous scale of evidence that Bayes factors represent. These classifications are heuristic and should not be misused as an absolute rule for all-or-nothing conclusions
When the goal of the analysis is parameter estimation, the posterior distribution is key (see Box 2). The posterior distribution is often summarized by a location parameter (point estimate) and uncertainty measure (interval estimate). For point estimation, the posterior median (reported by JASP), mean, or mode can be reported, although these do not contain any information about the uncertainty of the estimate. In order to capture the uncertainty of the estimate, an x % credible interval can be reported. The credible interval [ L , U ] has a x % probability that the true parameter lies in the interval that ranges from L to U (an interpretation that is often wrongly attributed to frequentist confidence intervals, see Morey, Hoekstra, Rouder, Lee, & Wagenmakers, 2016 ). For example, if we obtain a 95 % credible interval of [− 1,0.5] for effect size δ , we can be 95 % certain that the true value of δ lies between − 1 and 0.5, assuming that the alternative hypothesis we specify is true. In case one does not want to make this assumption, one can present the unconditional posterior distribution instead. For more discussion on this point, see Box 3.
Box 3. Conditional vs. unconditional inference.
A widely accepted view on statistical inference is neatly summarized by Fisher ( 1925 ), who states that “it is a useful preliminary before making a statistical estimate \(\dots \) to test if there is anything to justify estimation at all” (p. 300; see also Haaf, Ly, & Wagenmakers, 2019 ). In the Bayesian framework, this stance naturally leads to posterior distributions conditional on \({\mathscr{H}}_{1}\) , which ignores the possibility that the null value could be true. Generally, when we say “prior distribution” or “posterior distribution” we are following convention and referring to such conditional distributions. However, only presenting conditional posterior distributions can potentially be misleading in cases where the null hypothesis remains relatively plausible after seeing the data. A general benefit of Bayesian analysis is that one can compute an unconditional posterior distribution for the parameter using model averaging (e.g., Clyde, Ghosh, & Littman, 2011 ; Hinne, Gronau, Bergh, & Wagenmakers, 2020 ). An unconditional posterior distribution for a parameter accounts for both the uncertainty about the parameter within any one model and the uncertainty about the model itself, providing an estimate of the parameter that is a compromise between the candidate models (for more details see Hoeting, Madigan, Raftery, & Volinsky, 1999 ). In the case of a t test, which features only the null and the alternative hypothesis, the unconditional posterior consists of a mixture between a spike under \({\mathscr{H}}_{0}\) and a bell-shaped posterior distribution under \({\mathscr{H}}_{1}\) (Rouder, Haaf, & Vandekerckhove, 2018 ; van den Bergh, Haaf, Ly, Rouder, & Wagenmakers, 2019 ). Figure 5 illustrates this approach for the stereogram example.
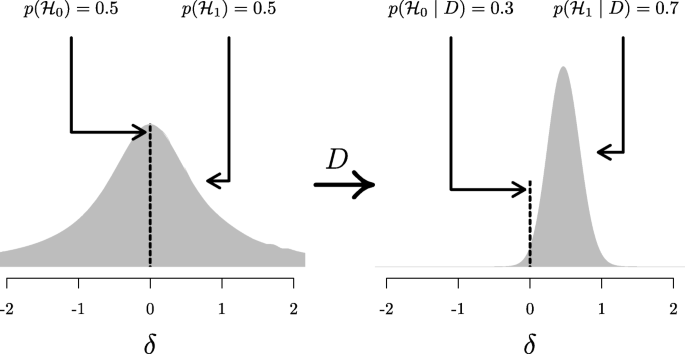
Updating the unconditional prior distribution to the unconditional posterior distribution for the stereogram example. The left panel shows the unconditional prior distribution, which is a mixture between the prior distributions under \({\mathscr{H}}_{0}\) and \({\mathscr{H}}_{1}\) . The prior distribution under \({\mathscr{H}}_{0}\) is a spike at the null value, indicated by the dotted line ; the prior distribution under \({\mathscr{H}}_{1}\) is a Cauchy distribution, indicated by the gray mass . The mixture proportion is determined by the prior model probabilities \(p({\mathscr{H}}_{0})\) and \(p({\mathscr{H}}_{1})\) . The right panel shows the unconditional posterior distribution, after updating the prior distribution with the data D . This distribution is a mixture between the posterior distributions under \({\mathscr{H}}_{0}\) and \({\mathscr{H}}_{1}\) ., where the mixture proportion is determined by the posterior model probabilities \(p({\mathscr{H}}_{0} \mid D)\) and \(p({\mathscr{H}}_{1} \mid D)\) . Since \(p({\mathscr{H}}_{1} \mid D) = 0.7\) (i.e., the data provide support for \({\mathscr{H}}_{1}\) over \({\mathscr{H}}_{0}\) ), about 70% of the unconditional posterior mass is comprised of the posterior mass under \({\mathscr{H}}_{1}\) , indicated by the gray mass . Thus, the unconditional posterior distribution provides information about plausible values for δ , while taking into account the uncertainty of \({\mathscr{H}}_{1}\) being true. In both panels, the dotted line and gray mass have been rescaled such that the height of the dotted line and the highest point of the gray mass reflect the prior ( left ) and posterior ( right ) model probabilities
Common pitfalls in interpreting Bayesian results
Bayesian veterans sometimes argue that Bayesian concepts are intuitive and easier to grasp than frequentist concepts. However, in our experience there exist persistent misinterpretations of Bayesian results. Here we list five:
The Bayes factor does not equal the posterior odds; in fact, the posterior odds are equal to the Bayes factor multiplied by the prior odds (see also Equation 1 ). These prior odds reflect the relative plausibility of the rival hypotheses before seeing the data (e.g., 50/50 when both hypotheses are equally plausible, or 80/20 when one hypothesis is deemed to be four times more plausible than the other). For instance, a proponent and a skeptic may differ greatly in their assessment of the prior plausibility of a hypothesis; their prior odds differ, and, consequently, so will their posterior odds. However, as the Bayes factor is the updating factor from prior odds to posterior odds, proponent and skeptic ought to change their beliefs to the same degree (assuming they agree on the model specification, including the parameter prior distributions).
Prior model probabilities (i.e., prior odds) and parameter prior distributions play different conceptual roles. Footnote 5 The former concerns prior beliefs about the hypotheses, for instance that both \({\mathscr{H}}_{0}\) and \({\mathscr{H}}_{1}\) are equally plausible a priori. The latter concerns prior beliefs about the model parameters within a model, for instance that all values of Pearson’s ρ are equally likely a priori (i.e., a uniform prior distribution on the correlation parameter). Prior model probabilities and parameter prior distributions can be combined to one unconditional prior distribution as described in Box 3 and Fig. 5 .
The Bayes factor and credible interval have different purposes and can yield different conclusions. Specifically, the typical credible interval for an effect size is conditional on \({\mathscr{H}}_{1}\) being true and quantifies the strength of an effect, assuming it is present (but see Box 3); in contrast, the Bayes factor quantifies evidence for the presence or absence of an effect. A common misconception is to conduct a “hypothesis test” by inspecting only credible intervals. Berger ( 2006 , p. 383) remarks: “[...] Bayesians cannot test precise hypotheses using confidence intervals. In classical statistics one frequently sees testing done by forming a confidence region for the parameter, and then rejecting a null value of the parameter if it does not lie in the confidence region. This is simply wrong if done in a Bayesian formulation (and if the null value of the parameter is believable as a hypothesis).”
The strength of evidence in the data is easy to overstate: a Bayes factor of 3 provides some support for one hypothesis over another, but should not warrant the confident all-or-none acceptance of that hypothesis.
The results of an analysis always depend on the questions that were asked. Footnote 6 For instance, choosing a one-sided analysis over a two-sided analysis will impact both the Bayes factor and the posterior distribution. For an illustration of this, see Fig. 6 for a comparison between one-sided and a two-sided results.
In order to avoid these and other pitfalls, we recommend that researchers who are doubtful about the correct interpretation of their Bayesian results solicit expert advice (for instance through the JASP forum at http://forum.cogsci.nl ).
For hypothesis testing, the results of the one-sided t test are presented in Fig. 6 a. The resulting BF + 0 is 4.567, indicating moderate evidence in favor of \({\mathscr{H}}_{+}\) : the data are approximately 4.6 times more likely under \({\mathscr{H}}_{+}\) than under \({\mathscr{H}}_{0}\) . To assess the robustness of this result, we also planned a Mann–Whitney U test. The resulting BF + 0 is 5.191, qualitatively similar to the Bayes factor from the parametric test. Additionally, we could have specified a multiverse analysis where data exclusion criteria (i.e., exclusion vs. no exclusion), the type of test (i.e., Mann–Whitney U vs. t test), and data transformations (i.e., log-transformed vs. raw fuse times) are varied. Typically in multiverse analyses these three decisions would be crossed, resulting in at least eight different analyses. However, in our case some of these analyses are implausible or redundant. First, because the Mann–Whitney U test is unaffected by the log transformation, the log-transformed and raw fuse times yield the same results. Second, due to the multiple assumption violations, the t test model for raw fuse times is misspecified and hence we do not trust the validity of its result. Third, we do not know which observations were excluded by (Frisby & Clatworthy, 1975 ). Consequently, only two of these eight analyses are relevant. Footnote 7 Furthermore, a more comprehensive multiverse analysis could also consider the Bayes factors from two-sided tests (i.e., BF 10 = 2.323) for the t test and BF 10 = 2.557 for the Mann–Whitney U test). However, these tests are not in line with the theory under consideration, as they answer a different theoretical question (see “Specifying the statistical model” in the Planning section).
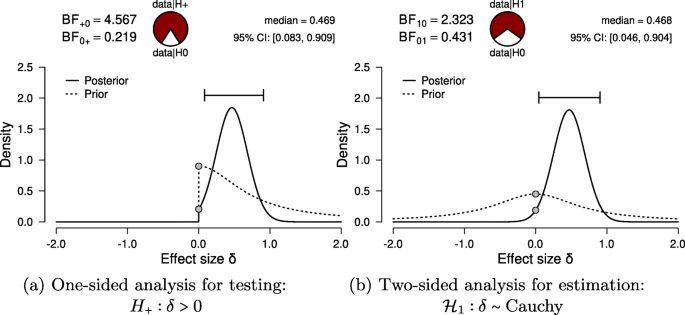
Bayesian two-sample t test for the parameter δ . The probability wheel on top visualizes the evidence that the data provide for the two rival hypotheses. The two gray dots indicate the prior and posterior density at the test value (Dickey & Lientz, 1970 ; Wagenmakers, Lodewyckx, Kuriyal, & Grasman, 2010 ). The median and the 95 % central credible interval of the posterior distribution are shown in the top right corner. The left panel shows the one-sided procedure for hypothesis testing and the right panel shows the two-sided procedure for parameter estimation. Both figures from JASP
For parameter estimation, the results of the two-sided t test are presented in Fig. 6 a. The 95 % central credible interval for δ is relatively wide, ranging from 0.046 to 0.904: this means that, under the assumption that the effect exists and given the model we specified, we can be 95 % certain that the true value of δ lies between 0.046 to 0.904. In conclusion, there is moderate evidence for the presence of an effect, and large uncertainty about its size.
Stage 4: Reporting the results
For increased transparency, and to allow a skeptical assessment of the statistical claims, we recommend to present an elaborate analysis report including relevant tables, figures, assumption checks, and background information. The extent to which this needs to be done in the manuscript itself depends on context. Ideally, an annotated .jasp file is created that presents the full results and analysis settings. The resulting file can then be uploaded to the Open Science Framework (OSF; https://osf.io ), where it can be viewed by collaborators and peers, even without having JASP installed. Note that the .jasp file retains the settings that were used to create the reported output. Analyses not conducted in JASP should mimic such transparency, for instance through uploading an R-script. In this section, we list several desiderata for reporting, both for hypothesis testing and parameter estimation. What to include in the report depends on the goal of the analysis, regardless of whether the result is conclusive or not.
In all cases, we recommend to provide a complete description of the prior specification (i.e., the type of distribution and its parameter values) and, especially for informed priors, to provide a justification for the choices that were made. When reporting a specific analysis, we advise to refer to the relevant background literature for details. In JASP, the relevant references for specific tests can be copied from the drop-down menus in the results panel.
When the goal of the analysis is hypothesis testing, it is key to outline which hypotheses are compared by clearly stating each hypothesis and including the corresponding subscript in the Bayes factor notation. Furthermore, we recommend to include, if available, the Bayes factor robustness check discussed in the section on planning (see Fig. 7 for an example). This check provides an assessment of the robustness of the Bayes factor under different prior specifications: if the qualitative conclusions do not change across a range of different plausible prior distributions, this indicates that the analysis is relatively robust. If this plot is unavailable, the robustness of the Bayes factor can be checked manually by specifying several different prior distributions (see the mixed ANOVA analysis in the online appendix at https://osf.io/wae57/ for an example). When data come in sequentially, it may also be of interest to examine the sequential Bayes factor plot, which shows the evidential flow as a function of increasing sample size.
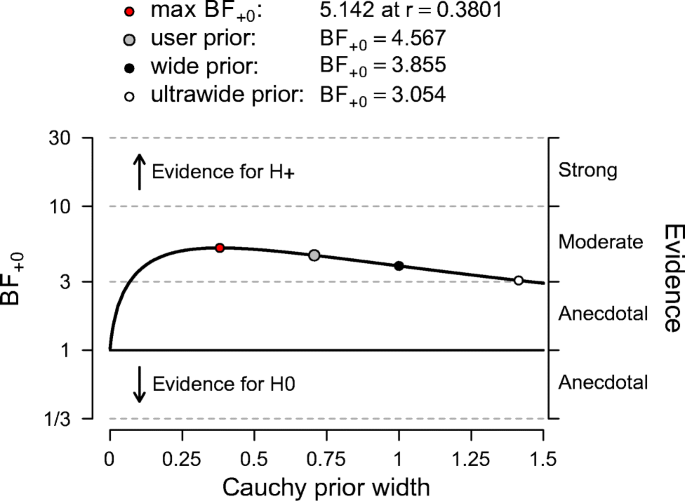
The Bayes factor robustness plot. The maximum BF + 0 is attained when setting the prior width r to 0.38. The plot indicates BF + 0 for the user specified prior ( \(r = {1}/{\sqrt {2}}\) ), wide prior ( r = 1), and ultrawide prior ( \(r = \sqrt {2}\) ). The evidence for the alternative hypothesis is relatively stable across a wide range of prior distributions, suggesting that the analysis is robust. However, the evidence in favor of \({\mathscr{H}}_{+}\) is not particularly strong and will not convince a skeptic
When the goal of the analysis is parameter estimation, it is important to present a plot of the posterior distribution, or report a summary, for instance through the median and a 95 % credible interval. Ideally, the results of the analysis are reported both graphically and numerically. This means that, when possible, a plot is presented that includes the posterior distribution, prior distribution, Bayes factor, 95 % credible interval, and posterior median. Footnote 8
Numeric results can be presented either in a table or in the main text. If relevant, we recommend to report the results from both estimation and hypothesis test. For some analyses, the results are based on a numerical algorithm, such as Markov chain Monte Carlo (MCMC), which yields an error percentage. If applicable and available, the error percentage ought to be reported too, to indicate the numeric robustness of the result. Lower values of the error percentage indicate greater numerical stability of the result. Footnote 9 In order to increase numerical stability, JASP includes an option to increase the number of samples for MCMC sampling when applicable.
This is an example report of the stereograms t test example:
Here we summarize the results of the Bayesian analysis for the stereogram data. For this analysis we used the Bayesian t test framework proposed by (see also; Jeffreys, 1961 ; Rouder et al., 2009 ). We analyzed the data with JASP (JASP Team, 2019 ). An annotated .jasp file, including distribution plots, data, and input options, is available at https://osf.io/25ekj/ . Due to model misspecification (i.e., non-normality, presence of outliers, and unequal variances), we applied a log-transformation to the fuse times. This remedied the misspecification. To assess the robustness of the results, we also applied a Mann–Whitney U test. First, we discuss the results for hypothesis testing. The null hypothesis postulates that there is no difference in log fuse time between the groups and therefore \({\mathscr{H}}_{0}: \delta = 0\) . The one-sided alternative hypothesis states that only positive values of δ are possible, and assigns more prior mass to values closer to 0 than extreme values. Specifically, δ was assigned a Cauchy prior distribution with \(r ={1}/{\sqrt {2}}\) , truncated to allow only positive effect size values. Figure 6 a shows that the Bayes factor indicates evidence for \({\mathscr{H}}_{+}\) ; specifically, BF + 0 = 4.567, which means that the data are approximately 4.5 times more likely to occur under \({\mathscr{H}}_{+}\) than under \({\mathscr{H}}_{0}\) . This result indicates moderate evidence in favor of \({\mathscr{H}}_{+}\) . The error percentage is < 0.001 % , which indicates great stability of the numerical algorithm that was used to obtain the result. The Mann–Whitney U test yielded a qualitatively similar result, BF + 0 is 5.191. In order to assess the robustness of the Bayes factor to our prior specification, Fig. 7 shows BF + 0 as a function of the prior width r . Across a wide range of widths, the Bayes factor appears to be relatively stable, ranging from about 3 to 5. Second, we discuss the results for parameter estimation. Of interest is the posterior distribution of the standardized effect size δ (i.e., the population version of Cohen’s d , the standardized difference in mean fuse times). For parameter estimation, δ was assigned a Cauchy prior distribution with \(r ={1}/{\sqrt {2}}\) . Figure 6 b shows that the median of the resulting posterior distribution for δ equals 0.47 with a central 95% credible interval for δ that ranges from 0.046 to 0.904. If the effect is assumed to exist, there remains substantial uncertainty about its size, with values close to 0 having the same posterior density as values close to 1.
Limitations and challenges
The Bayesian toolkit for the empirical social scientist still has some limitations to overcome. First, for some frequentist analyses, the Bayesian counterpart has not yet been developed or implemented in JASP. Secondly, some analyses in JASP currently provide only a Bayes factor, and not a visual representation of the posterior distributions, for instance due to the multidimensional parameter space of the model. Thirdly, some analyses in JASP are only available with a relatively limited set of prior distributions. However, these are not principled limitations and the software is actively being developed to overcome these limitations. When dealing with more complex models that go beyond the staple analyses such as t tests, there exist a number of software packages that allow custom coding, such as JAGS (Plummer, 2003 ) or Stan (Carpenter et al., 2017 ). Another option for Bayesian inference is to code the analyses in a programming language such as R (R Core Team, 2018 ) or Python (van Rossum, 1995 ). This requires a certain degree of programming ability, but grants the user more flexibility. Popular packages for conducting Bayesian analyses in R are the BayesFactor package (Morey & Rouder, 2015 ) and the brms package (Bürkner, 2017 ), among others (see https://cran.r-project.org/web/views/Bayesian.html for a more exhaustive list). For Python, a popular package for Bayesian analyses is PyMC3 (Salvatier, Wiecki, & Fonnesbeck, 2016 ). The practical guidelines provided in this paper can largely be generalized to the application of these software programs.
Concluding comments
We have attempted to provide concise recommendations for planning, executing, interpreting, and reporting Bayesian analyses. These recommendations are summarized in Table 1 . Our guidelines focused on the standard analyses that are currently featured in JASP. When going beyond these analyses, some of the discussed guidelines will be easier to implement than others. However, the general process of transparent, comprehensive, and careful statistical reporting extends to all Bayesian procedures and indeed to statistical analyses across the board.
The variables are participant number, the time (in seconds) each participant needed to see the hidden figure (i.e., fuse time), experimental condition (VV = with visual information, NV = without visual information), and the log-transformed fuse time.
A one-sided alternative hypothesis makes a more risky prediction than a two-sided hypothesis. Consequently, if the data are in line with the one-sided prediction, the one-sided alternative hypothesis is rewarded with a greater gain in plausibility compared to the two-sided alternative hypothesis; if the data oppose the one-sided prediction, the one-sided alternative hypothesis is penalized with a greater loss in plausibility compared to the two-sided alternative hypothesis.
The fat-tailed Cauchy distribution is a popular default choice because it fulfills particular desiderata, see (Jeffreys, 1961 ;Liang, German, Clyde, & Berger, 2008 ; Ly et al., 2016 ; Rouder, Speckman, Sun, Morey, & Iverson, 2009 ) for details.
Specifically, the proportion of red is the posterior probability of \({\mathscr{H}}_{1}\) under a prior probability of 0.5; for a more detailed explanation and a cartoon see https://tinyurl.com/ydhfndxa
This confusion does not arise for the rarely reported unconditional distributions (see Box 3).
This is known as Jeffreys’s platitude: “The most beneficial result that I can hope for as a consequence of this work is that more attention will be paid to the precise statement of the alternatives involved in the questions asked. It is sometimes considered a paradox that the answer depends not only on the observations but on the question; it should be a platitude” (Jeffreys, 1939 , p.vi).
The Bayesian Mann–Whitney U test results and the results for the raw fuse times are in the .jasp file at https://osf.io/nw49j/ .
The posterior median is popular because it is robust to skewed distributions and invariant under smooth transformations of parameters, although other measures of central tendency, such as the mode or the mean, are also in common use.
We generally recommend error percentages below 20% as acceptable. A 20% change in the Bayes factor will result in one making the same qualitative conclusions. However, this threshold naturally increases with the magnitude of the Bayes factor. For instance, a Bayes factor of 10 with a 50% error percentage could be expected to fluctuate between 5 and 15 upon recomputation. This could be considered a large change. However, with a Bayes factor of 1000 a 50% reduction would still leave us with overwhelming evidence.
Andrews, M., & Baguley, T. (2013). Prior approval: The growth of Bayesian methods in psychology. British Journal of Mathematical and Statistical Psychology , 66 , 1–7.
Google Scholar
Anscombe, F. J. (1973). Graphs in statistical analysis. The American Statistician , 27 , 17–21.
Appelbaum, M., Cooper, H., Kline, R. B., Mayo-Wilson, E., Nezu, A. M., & Rao, S. M. (2018). Journal article reporting standards for quantitative research in psychology: The APA Publications and Communications Board task force report. American Psychologist , 73 , 3–25.
Berger, J. O. (2006). Bayes factors. In S. Kotz, N. Balakrishnan, C. Read, B. Vidakovic, & N. L. Johnson (Eds.) Encyclopedia of Statistical Sciences, vol. 1, 378-386, Hoboken, NJ, Wiley .
Berger, J. O., & Wolpert, R. L. (1988) The likelihood principle , (2nd edn.) Hayward (CA): Institute of Mathematical Statistics.
Bürkner, P.C. (2017). brms: An R package for Bayesian multilevel models using Stan. Journal of Statistical Software , 80 , 1–28.
Carpenter, B., Gelman, A., Hoffman, M., Lee, D., Goodrich, B., Betancourt, M., & et al. (2017). Stan: A probabilistic programming language. Journal of Statistical Software , 76 , 1–37.
Clyde, M. A., Ghosh, J., & Littman, M. L. (2011). Bayesian adaptive sampling for variable selection and model averaging. Journal of Computational and Graphical Statistics , 20 , 80–101.
Depaoli, S., & Schoot, R. van de (2017). Improving transparency and replication in Bayesian statistics: The WAMBS-checklist. Psychological Methods , 22 , 240–261.
PubMed Google Scholar
Dickey, J. M., & Lientz, B. P. (1970). The weighted likelihood ratio, sharp hypotheses about chances, the order of a Markov chain. The Annals of Mathematical Statistics , 41 , 214–226.
Dienes, Z. (2014). Using Bayes to get the most out of non-significant results. Frontiers in Psychology , 5 , 781.
PubMed PubMed Central Google Scholar
Draper, N. R., & Cox, D. R. (1969). On distributions and their transformation to normality. Journal of the Royal Statistical Society: Series B (Methodological) , 31 , 472–476.
Etz, A. (2018). Introduction to the concept of likelihood and its applications. Advances in Methods and Practices in Psychological Science , 1 , 60–69.
Etz, A., Haaf, J. M., Rouder, J. N., & Vandekerckhove, J. (2018). Bayesian inference and testing any hypothesis you can specify. Advances in Methods and Practices in Psychological Science , 1 (2), 281–295.
Etz, A., & Wagenmakers, E. J. (2017). J. B. S. Haldane’s contribution to the Bayes factor hypothesis test. Statistical Science , 32 , 313–329.
Fisher, R. (1925). Statistical methods for research workers, (12). Edinburgh Oliver & Boyd.
Frisby, J. P., & Clatworthy, J. L. (1975). Learning to see complex random-dot stereograms. Perception , 4 , 173–178.
Gronau, Q. F., Ly, A., & Wagenmakers, E. J. (2020). Informed Bayesian t tests. The American Statistician , 74 , 137–143.
Haaf, J., Ly, A., & Wagenmakers, E. (2019). Retire significance, but still test hypotheses. Nature , 567 (7749), 461.
Hinne, M., Gronau, Q. F., Bergh, D., & Wagenmakers, E. J. (2020). Van den A conceptual introduction to Bayesian model averaging. Advances in Methods and Practices in Psychological Science , 3 , 200–215.
Hoeting, J. A., Madigan, D., Raftery, A. E., & Volinsky, C. T. (1999). Bayesian model averaging: a tutorial. Statistical science, 382–401.
JASP Team (2019). JASP (Version 0.9.2)[Computer software]. https://jasp-stats.org/ .
Jarosz, A. F., & Wiley, J. (2014). What are the odds? A practical guide to computing and reporting Bayes factors. Journal of Problem Solving , 7 , 2–9.
Jeffreys, H. (1939). Theory of probability, 1st. Oxford University Press.
Jeffreys, H. (1961). Theory of probability. 3rd. Oxford University Press.
Kass, R. E., & Raftery, A. E. (1995). Bayes factors. Journal of the American Statistical Association , 90 , 773–795.
Keysers, C., Gazzola, V., & Wagenmakers, E. J. (2020). Using Bayes factor hypothesis testing in neuroscience to establish evidence of absence. Nature Neuroscience , 23 , 788–799.
Lee, M. D., & Vanpaemel, W. (2018). Determining informative priors for cognitive models. Psychonomic Bulletin & Review , 25 , 114–127.
Liang, F., German, R. P., Clyde, A., & Berger, J. (2008). Mixtures of G priors for Bayesian variable selection. Journal of the American Statistical Association , 103 , 410–424.
Lo, S., & Andrews, S. (2015). To transform or not to transform: Using generalized linear mixed models to analyse reaction time data. Frontiers in Psychology , 6 , 1171.
Ly, A., Verhagen, A. J., & Wagenmakers, E. J. (2016). Harold Jeffreys’s default Bayes factor hypothesis tests: Explanation, extension, and application in psychology. Journal of Mathematical Psychology , 72 , 19–32.
Marsman, M., & Wagenmakers, E. J. (2017). Bayesian benefits with JASP. European Journal of Developmental Psychology , 14 , 545–555.
Matzke, D., Nieuwenhuis, S., van Rijn, H., Slagter, H. A., van der Molen, M. W., & Wagenmakers, E. J. (2015). The effect of horizontal eye movements on free recall: A preregistered adversarial collaboration. Journal of Experimental Psychology: General , 144 , e1–e15.
Morey, R. D., Hoekstra, R., Rouder, J. N., Lee, M. D., & Wagenmakers, E. J. (2016). The fallacy of placing confidence in confidence intervals. Psychonomic Bulletin & Review , 23 , 103–123.
Morey, R. D., & Rouder, J. N. (2015). BayesFactor 0.9.11-1. Comprehensive R Archive Network. http://cran.r-project.org/web/packages/BayesFactor/index.html .
Plummer, M. (2003). JAGS: A Program for analysis of Bayesian graphical models using Gibbs sampling. In K. Hornik, F. Leisch, & A. Zeileis (Eds.) Proceedings of the 3rd international workshop on distributed statistical computing, Vienna, Austria .
R Core Team (2018). R: A language and environment for statistical computing [Computer software manual]. Vienna, Austria. https://www.R-project.org/ .
Rouder, J. N. (2014). Optional stopping: No problem for Bayesians. Psychonomic Bulletin & Review , 21 , 301–308.
Rouder, J. N., Haaf, J. M., & Vandekerckhove, J. (2018). Bayesian inference for psychology, part IV: Parameter estimation and Bayes factors. Psychonomic Bulletin & Review , 25 (1), 102–113.
Rouder, J. N., Speckman, P. L., Sun, D., Morey, R. D., & Iverson, G. (2009). Bayesian t tests for accepting and rejecting the null hypothesis. Psychonomic Bulletin & Review , 16 , 225– 237.
Salvatier, J., Wiecki, T. V., & Fonnesbeck, C. (2016). Probabilistic programming in Python using pyMC. PeerJ Computer Science , 3 (2), e55.
Schönbrodt, F.D., & Wagenmakers, E. J. (2018). Bayes factor design analysis: Planning for compelling evidence. Psychonomic Bulletin & Review , 25 , 128–142.
Schramm, P., & Rouder, J. N. (2019). Are reaction time transformations really beneficial? PsyArXiv, March 5.
Spiegelhalter, D. J., Myles, J. P., Jones, D. R., & Abrams, K. R. (2000). Bayesian methods in health technology assessment: a review. Health Technology Assessment , 4 , 1–130.
Steegen, S., Tuerlinckx, F., Gelman, A., & Vanpaemel, W. (2016). Increasing transparency through a multiverse analysis. Perspectives on Psychological Science , 11 , 702–712.
Stefan, A. M., Gronau, Q. F., Schönbrodt, F.D., & Wagenmakers, E. J. (2019). A tutorial on Bayes factor design analysis using an informed prior. Behavior Research Methods , 51 , 1042–1058.
Sung, L., Hayden, J., Greenberg, M. L., Koren, G., Feldman, B. M., & Tomlinson, G. A. (2005). Seven items were identified for inclusion when reporting a Bayesian analysis of a clinical study. Journal of Clinical Epidemiology , 58 , 261–268.
The BaSiS group (2001). Bayesian standards in science: Standards for reporting of Bayesian analyses in the scientific literature. Internet. http://lib.stat.cmu.edu/bayesworkshop/2001/BaSis.html .
Tijmstra, J. (2018). Why checking model assumptions using null hypothesis significance tests does not suffice: a plea for plausibility. Psychonomic Bulletin & Review , 25 , 548–559.
Vandekerckhove, J., Rouder, J. N., & Kruschke, J. K. (eds.) (2018). Beyond the new statistics: Bayesian inference for psychology [special issue]. Psychonomic Bulletin & Review , p 25.
Wagenmakers, E. J., Beek, T., Rotteveel, M., Gierholz, A., Matzke, D., Steingroever, H., & et al. (2015). Turning the hands of time again: A purely confirmatory replication study and a Bayesian analysis. Frontiers in Psychology: Cognition , 6 , 494.
Wagenmakers, E. J., Lodewyckx, T., Kuriyal, H., & Grasman, R. (2010). Bayesian hypothesis testing for psychologists: A tutorial on the Savage–Dickey method. Cognitive Psychology , 60 , 158–189.
Wagenmakers, E. J., Love, J., Marsman, M., Jamil, T., Ly, A., Verhagen, J., & et al. (2018). Bayesian inference for psychology. Part II: Example applications with JASP. Psychonomic Bulletin &, Review , 25 , 58–76.
Wagenmakers, E. J., Marsman, M., Jamil, T., Ly, A., Verhagen, J., Love, J., & et al. (2018). Bayesian inference for psychology. Part I: Theoretical advantages and practical ramifications. Psychonomic Bulletin &, Review , 25 , 35–57.
Wagenmakers, E. J., Morey, R. D., & Lee, M. D. (2016). Bayesian benefits for the pragmatic researcher. Current Directions in Psychological Science , 25 , 169–176.
Wetzels, R., Raaijmakers, J. G. W., Jakab, E., & Wagenmakers, E. J. (2009). How to quantify support for and against the null hypothesis: A flexible winBUGS implementation of a default Bayesian t test. Psychonomic Bulletin & Review , 16 , 752– 760.
Wicherts, J. M., Veldkamp, C. L. S., Augusteijn, H. E. M., Bakker, M., van Aert, R. C. M., & van Assen, M. A. L. M. (2016). Degrees of freedom in planning, running, analyzing, and reporting psychological studies: A checklist to avoid p-hacking. Frontiers in Psychology , 7 , 1832.
Wrinch, D., & Jeffreys, H. (1921). On certain fundamental principles of scientific inquiry. Philosophical Magazine , 42 , 369– 390.
van Doorn, J., Ly, A., Marsman, M., & Wagenmakers, E. J. (2020). Bayesian rank-based hypothesis testing for the rank sum test, the signed rank test, and spearman’s rho. Journal of Applied Statistics , 1–23.
van Rossum, G. (1995). Python tutorial (Tech. Rep. No. CS-R9526). Amsterdam: Centrum voor Wiskunde en Informatica (CWI).
van den Bergh, D., Haaf, J. M., Ly, A., Rouder, J. N., & Wagenmakers, E. J. (2019). A cautionary note on estimating effect size. PsyArXiv. Retrieved from psyarxiv.com/h6pr8 .
Download references
Acknowledgments
We thank Dr. Simons, two anonymous reviewers, and the editor for comments on an earlier draft. Correspondence concerning this article may be addressed to Johnny van Doorn, University of Amsterdam, Department of Psychological Methods, Valckeniersstraat 59, 1018 XA Amsterdam, the Netherlands. E-mail may be sent to [email protected]. This work was supported in part by a Vici grant from the Netherlands Organization of Scientific Research (NWO) awarded to EJW (016.Vici.170.083) and an advanced ERC grant awarded to EJW (743086 UNIFY). DM is supported by a Veni Grant (451-15-010) from the NWO. MM is supported by a Veni Grant (451-17-017) from the NWO. AE is supported by a National Science Foundation Graduate Research Fellowship (DGE1321846). Centrum Wiskunde & Informatica (CWI) is the national research institute for mathematics and computer science in the Netherlands.
Author information
Authors and affiliations.
University of Amsterdam, Amsterdam, Netherlands
Johnny van Doorn, Don van den Bergh, Udo Böhm, Fabian Dablander, Tim Draws, Nathan J. Evans, Quentin F. Gronau, Julia M. Haaf, Max Hinne, Šimon Kucharský, Alexander Ly, Maarten Marsman, Dora Matzke, Akash R. Komarlu Narendra Gupta, Alexandra Sarafoglou, Angelika Stefan & Eric-Jan Wagenmakers
Nyenrode Business University, Breukelen, Netherlands
University of California, Irvine, California, USA
Alexander Etz
Centrum Wiskunde & Informatica, Amsterdam, Netherlands
Alexander Ly
Stanford University, Stanford, California, USA
Jan G. Voelkel
You can also search for this author in PubMed Google Scholar
Contributions
JvD wrote the main manuscript. EJW, AE, JH, and JvD contributed to manuscript revisions. All authors reviewed the manuscript and provided feedback.
Corresponding author
Correspondence to Johnny van Doorn .
Additional information
Publisher’s note.
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Open Practices Statement
The data and materials are available at https://osf.io/nw49j/ .
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .
Reprints and permissions
About this article
van Doorn, J., van den Bergh, D., Böhm, U. et al. The JASP guidelines for conducting and reporting a Bayesian analysis. Psychon Bull Rev 28 , 813–826 (2021). https://doi.org/10.3758/s13423-020-01798-5
Download citation
Published : 09 October 2020
Issue Date : June 2021
DOI : https://doi.org/10.3758/s13423-020-01798-5
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Bayesian inference
- Scientific reporting
- Statistical software
- Find a journal
- Publish with us
- Track your research
An Introduction to Data Analysis
11 bayesian hypothesis testing.
This chapter introduces common Bayesian methods of testing what we could call statistical hypotheses . A statistical hypothesis is a hypothesis about a particular model parameter or a set of model parameters. Most often, such a hypothesis concerns one parameter, and the assumption in question is that this parameter takes on a specific value, or some value from a specific interval. Henceforth, we speak just of a “hypothesis” even though we mean a specific hypothesis about particular model parameters. For example, we might be interested in what we will call a point-valued hypothesis , stating that the value of parameter \(\theta\) is fixed to a specific value \(\theta = \theta^*\) . Section 11.1 introduces different kinds of statistical hypotheses in more detail.
Given a statistical hypothesis about parameter values, we are interested in “testing” it. Strictly speaking, the term “testing” should probably be reserved for statistical decision procedures which give clear categorical judgements, such as whether to reject a hypothesis, accept it as true or to withhold judgement because no decision can be made (yet/currently). While we will encounter such categorical decision routines in this chapter, Bayesian approaches to hypotheses “testing” are first and foremost concerned, not with categorical decisions, but with quantifying evidence in favor or against the hypothesis in question. (In a second step, using Bayesian decision theory which also weighs in the utility of different policy choices, we can use Bayesian inference also for informed decision making, of course.) But instead of speaking of “Bayesian inference to weigh evidence for/against a hypothesis” we will just speak of “Bayesian hypothesis testing” for ease of parlor.
We consider two conceptually distinct approaches within Bayesian hypothesis testing.
- Estimation-based testing considers just one model. It uses the observed data \(D_\text{obs}\) to retrieve posterior beliefs \(P(\theta \mid D_{\text{obs}})\) and checks whether, a posteriori , our hypothesis is credible.
- Comparison-based testing uses Bayesian model comparison, in the form of Bayes factors, to compare two models, namely one model that assumes that the hypothesis in question is true, and one model that assumes that the complement of the hypothesis is true.
The main difference between these two approaches is that estimation-based hypothesis testing is simpler (conceptually and computationally), but less informative than comparison-based hypothesis testing. In fact, comparison-based methods give a clearer picture of the quantitative evidence for/against a hypothesis because they explicitly take into account a second alternative to the hypothesis which is to be tested. As we will see in this chapter, the technical obstacles for comparison-based approaches can be overcome. For special but common use cases, like testing directional hypotheses, there are efficient methods of performing comparison-based hypothesis testing.
The learning goals for this chapter are:
- point-valued, ROPE-d and directional hypotheses
- complement / alternative hypothesis
- be able to apply Bayesian hypothesis testing to (simple) case studies
- understand and be able to apply the Savage-Dickey method (and its extension to interval-based hypotheses in terms of encompassing models )
- become familiar with a Bayesian \(t\) -test model for comparing the means of two groups of metric measurements
Last updated 27/06/24: Online ordering is currently unavailable due to technical issues. We apologise for any delays responding to customers while we resolve this. For further updates please visit our website: https://www.cambridge.org/news-and-insights/technical-incident
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings .
Login Alert

- > Statistical Hypothesis Testing in Context
- > Bayesian Hypothesis Testing

Book contents
- Frontmatter
- 1 Introduction
- 2 Theory of Tests, p-Values, and Confidence Intervals
- 3 From Scientific Theory to Statistical Hypothesis Test
- 4 One-Sample Studies with Binary Responses
- 5 One-Sample Studies with Ordinal or Numeric Responses
- 6 Paired Data
- 7 Two-Sample Studies with Binary Responses
- 8 Assumptions and Hypothesis Tests
- 9 Two-Sample Studies with Ordinal or Numeric Responses
- 10 General Methods for Frequentist Inferences
- 11 k-Sample Studies and Trend Tests
- 12 Clustering and Stratification
- 13 Multiplicity in Testing
- 14 Testing from Models
- 15 Causality
- 16 Censoring
- 17 Missing Data
- 18 Group Sequential and Related Adaptive Methods
- 19 Testing Fit, Equivalence, and Noninferiority
- 20 Power and Sample Size
- 21 Bayesian Hypothesis Testing
- Notation Index
- Concept Index
21 - Bayesian Hypothesis Testing
Published online by Cambridge University Press: 17 April 2022
This chapter gives a brief overview of Bayesian hypothesis testing. We first describe a standard Bayesian analysis of a single binomial response, going through the prior distribution choice and explaining how the posterior is calculated. We then discuss Bayesian hypothesis testing using the Bayes factor, a measure of how much the posterior odds of believing in one hypothesis changes from the prior odds. We show, using a binomial example, how the Bayes factor may be highly dependent on the prior distribution, even with extremely large sample sizes. We next discuss Bayes hypothesis testing using decision theory, reviewing the intrinsic discrepancy of Bernardo, as well as the loss functions proposed by Freedman. Freedman’s loss functions allow the posterior belief in the null hypothesis to equal the p-value. We next discuss well-calibrated null preferences priors, which applied to parameters from the natural exponential family (binomial, negative binomial, Poisson, normal), also give the posterior belief in the null hypothesis equal to valid one-sided p-values, and give credible intervals equal to valid confidence intervals.
Access options
Save book to kindle.
To save this book to your Kindle, first ensure [email protected] is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle .
Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.
Find out more about the Kindle Personal Document Service .
- Bayesian Hypothesis Testing
- Michael P. Fay , Erica H. Brittain
- Book: Statistical Hypothesis Testing in Context
- Online publication: 17 April 2022
- Chapter DOI: https://doi.org/10.1017/9781108528825.022
Save book to Dropbox
To save content items to your account, please confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your account. Find out more about saving content to Dropbox .
Save book to Google Drive
To save content items to your account, please confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your account. Find out more about saving content to Google Drive .
Statistics and Research Design
4 introduction to bayesian hypothesis testing.
In this chapter, we will be exploring how you can perform hypothesis testing under a Bayesian framework. After working through some interactive apps to understand the logic behind Bayesian statistics and Bayes factors, we will calculate Bayes factors for two independent samples and two dependent samples using real data. The application of Bayes factors still mostly relies on testing against a point null hypothesis, so we will end on an alternative known as a Region of Practical Equivalence (ROPE). Here, we try to reject parameter values inside boundaries for your smallest effect size of interest.
4.1 Learning objectives
By the end of this chapter, you should be able to:
Understand the logic behind Bayesian inference using the sweet example and Shiny app.
Use the online visualisation to explore what impacts Bayes factors .
Calculate Bayes factors for two independent samples .
Calculate Bayes factors for two dependent samples .
Define a Region of Practical Equivalence (ROPE) as an alternative to null hypothesis testing.
To follow along to this chapter and try the code yourself, please download the data files we will be using in this zip file .
Credit for sourcing three of the data sets goes to the Open Stats Lab and its creator Dr. Kevin McIntyre. The project provides a great resource for teaching exercises using open data.
4.2 The Logic Behind Bayesian Inference
To demonstrate the logic behind Bayesian inference, we will play around with this shiny app by Wagenmakers (2015) . The text walks you through the app and provides exercises to explore on your own, but we will use it to explore defining a prior distribution and seeing how the posterior updates with data.
The example is based on estimating the the proportion of yellow candies in a bag with different coloured candies. If you see a yellow candy, it is logged as a 1. If you see a non-yellow candy, it is logged as a 0. We want to know what proportion of the candies are yellow.
This is a handy demonstration for the logic behind Bayesian inference as it is the simplest application. Behind the scenes, we could calculate these values directly as the distributions are simple and there is only one parameter. In later examples and in lesson 10, we will focus on more complicated models which require sampling from the posterior.
4.2.1 Step 1 - Pick your prior
First, we define what our prior expectations are for the proportion of yellow candies. For a dichotomous outcome like this (yellow or not yellow), we can model the prior as a beta distribution . There are only two parameters to set: a and b .
Explore changing the parameters and their impact on the distribution, but here are a few observations to orient yourself:
Setting both to 1 create a flat prior: any proportion is possible.
Using the same number for both centers the distribution on 0.5, with increasing numbers showing greater certainty (higher peak).
If parameter a < b, proportions less than 0.5 are more likely.
If parameter b > a, proportions higher than 0.5 are more likely.
After playing around, what proportion of yellow candies do you think are likely? Are you certain about the value or are you more accepting of the data?
4.2.2 Step 2 - Update-to-a-posterior
Now we have a prior, its time to collect some data and update to the posterior. In the lecture, we will play around with a practical demonstration of seeing how many candies are yellow, so set your prior by entering a value for a and b , and we will see what the data tell us. There are two boxes for entering data: the number of yellows you observe, and the number of non-yellows you observe.
If you are trying this on your own, explore changing the prior and data to see how it affects the posterior distribution. For some inspiration and key observations:
Setting an uninformative (1,1) or weak prior (2, 2) over 0.5, the posterior is dominated by the data. For example, imagine we observed 5 yellows and 10 non-yellows. The posterior peaks around 0.30 but plausibly ranges between 0.2 and 0.6. Changing the data completely changes the posterior to show the prior has very little influence. As you change the number of yellows and non-yellows, the posterior updates more dramatically.
Now set a strong prior (20, 20) over 0.5 with 5 yellows and 10 non-yellows. Despite the observed data showing a proportion of 0.33, the peak of the posterior distribution is slightly higher than 0.4. The posterior is a compromise between the prior and the likelihood, so a stronger prior means you need more data to change your beliefs. For example, imagine we had 10 times more data with 50 yellows and 100 non-yellows. Now, there is greater density between 0.3 and 0.4, to show the posterior is now more convinced of the proportion of yellows.
In this demonstration, note we only have two curves for the prior and posterior, without the likelihood. When the prior and posterior come from the same distribution family, it is known as a conjugate prior , and the beta distribution is one of the simplest. We are simply modelling the proportion of successes and failures (here yellows vs non-yellows).
In section 4 of the app, you can also explore Bayes factors applied to this scenario, working out how much you should shift your belief in favour of the alternative hypothesis compared to the null (here, that the proportion is exactly 0.5). At this point of the lecture, we have not explored Bayes factors yet, so we will not continue with it here.
4.3 The Logic Behind Bayes Factors
To demonstrate the logic behind Bayes factors, we will play around with this interactive app by Magnusson . Building on section 1 , the visualisation shows a Bayesian two-sample t-test, demonstrating a more complicated application compared to the beta distribution and proportions. The visualisation shows both Bayesian estimation through the posterior distribution and 95% Highest Density Interval (HDI), and Bayes factors against a null hypothesis centered on 0. We will use this visualisation to reinforce what we learnt earlier and extend it to understanding the logic behind Bayes factors.
There are three settings on the visualisation, :
Observed effect - Expressed as Cohen's d, this represents the standardised mean difference between two groups. You can set larger effects (positive or negative) or assume the null hypothesis is true (d = 0).
Sample size - You can increase the sample size from 1 to 1000, with more steps between 1 and 100.
SD of prior - The prior is always set to 0 as we are testing against the null hypothesis, but you can specify how strong this prior is. Decreasing the SD means you are more confident in an effect of 0. Increasing the SD means you are less certain about the prior.
This visualisation is set up to test against the null hypothesis of no difference between two groups, but remember Bayes factors allow you to test any two hypotheses. The Bayes factor is represented by the difference between the two dots, where the curves represent a likelihood of 0 in the prior and posterior distributions. The Bayes factor is a ratio between these two values for the posterior odds of how much your belief should shift in favour of the experimental hypothesis compared to the null hypothesis.
Keep an eye on the p -value and 95% Confidence Interval (CI) to see where the inferences are similiar or different for each statistical philosophy.
To reinforce the lessons from section 1 and the emphasis now on Bayes factors, there are some key observations:
With a less informative prior (higher SD), the posterior is dominated by the likelihood to show the posterior is overwhelmed by data. For example, if you set the SD to 2, the prior peaks at 0 but the distribution is so flat it accepts any reasonable effect. If you move the observed effect anywhere along the scale, the likelihood and posterior almost completely overlap until you reach d = ±2.
With a stronger prior (lower SD), the posterior represents more of a compromise between the prior and likelihood. If you change the SD to 0.5 and the observed effect to 1, the posterior is closer to being an intermediary. You may have the observed data, but your prior belief in a null effect is strong enough that it requires more data to be convinced otherwise.
With more participants / data, there is less uncertainty in the likelihood. Keeping the same inputs as point 2, with 10 participants, the likelihood peaks at d = 1, but easily spans between 0 and 2. As you increase the sample size towards 1000, the uncertainty around the likelihood is lower. More data also overwhelms the prior, so although we had a relatively strong prior that we would have a null effect, with 50 participants, the likelihood and posterior mostly overlap.
Focusing on the Bayes factor supporting the experimental hypothesis, if there is an effect, evidence in favour of the experimental hypothesis increases as the observed effect increases or the sample size increases. This is not too dissimilar to frequentist statistical power, but with Bayesian statistics, optional stopping can be less of a problem ( Rouder ( 2014 ) but see Schönbrodt et al. ( 2017 ) for considerations you must make). So, if we do not have enough data to shift our beliefs towards either hypothesis, we can collect more data and update our beliefs.
If we set the observed effect to 0, the p -value is 1 to suggest we cannot reject the null, but remember we cannot support the null. With Bayes factors, we can support the null and see with observed effect = 0, sample size = 50, and SD of prior = 0.5, the data are 2.60 times more likely under the null than the experimental hypothesis. So, we should shift our belief in favour of the null, but it is not very convincing. We can obtain a higher Bayes factor in support of the null by increasing the sample size or increasing the SD of the prior. This last part might sound a little odd at first, but if your prior was very strong in favour of the null (small SD), your beliefs do not need to shift in light of the data.
Finally, if you set a weak prior (SD = 2), you will see the frequentist 95% CI and the Bayesian 95% HDI are almost identical. With a weak or uninformative prior, the values from the two intervals are usually similar, but you must interpret them differently. Increasing the sample size makes both intervals smaller and changing the observed effect shifts them around. If you make a stronger prior (SD = 0.5), now the 95% HDI will change as you move the observed effect size around. The frequentist 95% CI will always follow the likelihood as it is only based on the observed data. The Bayesian 95% HDI represents the area of the posterior, so it will be a compromise between the prior and likelihood, or it can be smaller if you have a stronger prior in favour of the null and an observed effect of 0.
Based on the observations above, try and apply your understanding to the questions below using Magnusson's interactive app.
Assuming a moderate effect size of d = 0.4 and a weak prior SD = 0.5, how many participants per group would you need for the Bayes factor to be 3 or more in favour of the alternative hypothesis?
Assuming a moderate effect size of d = 0.4 and 50 participants per group, when you use a weaker prior of SD = 2, evidence in favour of the alternative hypothesis is stronger weaker the same than when you use a stronger prior of SD = 1.
This is the opposite of point 5 in the explanation above. Remember Bayes factors represent a shift in belief in one hypothesis compared to another. If you are more confident in the null (smaller SD), then it would take more evidence to shift your belief in favour of the alternative hypothesis that there is a difference.
- The old rule of thumb in psychology was 20 participants per group would provide sufficient statistical power. Assuming a moderate effect size of d = 0.5 and a prior SD = 1, the difference would be statistically significant ( p = .049). However, looking at the guidelines provided in the lecture from Wagenmakers et al. ( 2011 ) , how could you describe the evidence in favour of the alternative hypothesis? No evidence Anecdotal Substantial Strong
4.4 Bayes factors for two independent samples
4.4.1 guided example (bastian et al., 2014).
This is the first time we have used R in this chapter, so we need to load some packages and the data for this task. If you do not have any of the packages, make sure you install them first.
For this guided example, we will reanalyse data from Bastian et al. ( 2014 ) . This study wanted to investigate whether experiencing pain together can increase levels of bonding between participants. The study was trying to explain how people often say friendships are strengthened by adversity.
Participants were randomly allocated into two conditions: pain or control. Participants in the pain group experienced mild pain through a cold pressor task (leaving your hand in ice cold water) and a wall squat (sitting against a wall). The control group completed a different task that did not involve pain. The participants then completed a scale to measure how bonded they felt to other participants in the group. Higher values on this scale mean greater bonding.
The independent variable is called "CONDITION" . The control group has the value 0 and the pain group has the value 1. They wanted to find out whether participants in the pain group would have higher levels of bonding with their fellow participants than participants in the control group. After a little processing, the dependent variable is called "mean_bonding" for the mean of 7 items related to bonding.
This chapter will predominantly use the BayesFactor package ( Morey & Rouder, 2022 ) and its functions applied to t-tests. To use the Bayesian version of the t-test, we use similar arguments to the base frequentist version by stating our design with a formula and which data frame you are referring to. For this study, we want to predict the bonding rating by the group they were allocated into: mean_bonding ~ CONDITION .
As we are using t-tests, keep in mind we are still applying a linear model to the data despite using Bayesian rather than frequentist statistics to model uncertainty. We are not going to cover it in this chapter, but you would still check your data for parametric assumptions like normal residuals and influential cases / outliers.
In the Bayesian t-test, we are comparing the null hypothesis of 0 against an alternative hypothesis. For our data in an independent samples t-test, we have the difference between our two groups. The prior for the null is a point-null hypothesis assuming the difference is 0, while the prior for the alternative is modelled as a Cauchy distribution. The Bayes factor tells you how much you should shift your belief towards one hypothesis compared to another, either in favour of the alternative or null hypothesis.
In the Bayesian t-test function, the main new argument is rscale which sets the width of the prior distribution around the alternative hypothesis. T-tests use a Cauchy prior which is similar to a normal distribution but with fatter tails and you only have to define one parameter: the r scale. The figure below visualises the difference between a Cauchy and normal distribution for the same range of r scale and SD values.

The default prior is set to "medium" , but you could change this depending on your understanding of the area of research. See the function help page for different options here, but medium is equivalent to a value of 0.707 for scaling the Cauchy prior which is the default setting for most statistics software. You can interpret the r scale as 50% of the distribution covers values ± your chosen value. An effect of zero is the most likely, but the larger the r scale value, the more plausible you consider large effects. If you use a value of 0.707 ( "medium" ) on a two-tailed test, this means 50% of the prior distribution covers values between ± 0.707. You can enter a numeric value for the precise scaling or there are a few word presets like "medium" , "wide" , and "ultrawide" depending on how strong or weak you want the prior to be.
Don't worry about the warning, there were just previous issues with using tibbles in the BayesFactor package. Now the package converts tibbles to normal R data frames before doing its thing.
With the medium prior, we have a Bayes factor of 1.45 ( \(BF\) \(_1\) \(_0\) = 1.45), suggesting the experimental hypothesis is 1.45 times more likely than the point null hypothesis. By the guidelines from Wagenmakers et al. (2011), this is quite weak anecdotal evidence.
There is also a percentage next to the Bayes factor. This is the proportional error estimate and tells you the error in estimating the Bayes factor value. Less error is better and a rough rule of thumb is less than 20% is acceptable ( Doorn et al., 2021 ) . In this example, the error estimate is 0.01%, so very small. This means we could expect the Bayes factor to range between 1.44 and 1.45 which makes little impact on the conclusion.
4.4.1.1 Robustness check
This will be more important for modelling in the next chapter, but it is good practice to check the sensitivity of your results to your choice of prior. You would exercise caution if your choice of prior affects the conclusions you are making, such as weak evidence turning into strong evidence. If the qualitative conclusions do not change across plausible priors, then your findings are robust. For example, the Bayes factor for the Bastian et al. example decreases as the prior r scale increases.
| Prior | BayesFactor |
|---|---|
| Medium | 1.45 |
| Wide | 1.22 |
| Ultrawide | 0.97 |
A wider prior expresses less certainty about the size of the effect; larger effects become more plausible. Remember Bayes factors quantify the degree of belief in one hypothesis compared to another. As the evidence is quite weak, the Bayes factor decreases in favour of the null under weaker priors as you are expressing less certainty about the size of the effect.
4.4.1.2 One- vs two-tailed tests
The authors were pretty convinced that the pain group would score higher on the bonding rating than the control group, so lets see what happens with a one-tailed test to see how its done. We need to define the nullInterval argument to state we only consider negative effects.
Make sure you check the order of your groups to check which direction you expect the results to go in. If you expect group A to be smaller than group B, you would code for negative effects. If you expect group A to be bigger than group B, you would code for positive effects. A common mistake is defining the wrong direction if you do not know which order the groups are coded.
In a one-tailed test, we now have two tests. In row one, we have the test we want where we compare our experimental hypothesis (negative effects) against the point null. In row two, we have the opposite which is the complement of our experimental hypothesis, which would be that the effect is not negative. Even with a one-tailed test, the evidence in favour of our experimental hypothesis compared to the null is anecdotal at best ( \(BF\) \(_1\) \(_0\) = 2.79).
If we wanted to test the null compared to the experimental hypothesis, we can simply take the reciprocal of the object, here demonstrated on the two-tailed object.
For this object, we already know there is anecdotal evidence in favour of the experimental hypothesis, so this is just telling us the null is less likely than the experimental hypothesis ( \(BF\) \(_0\) \(_1\) = 0.69). This will come in handy when you specifically want to test the null though.
For the purposes of the rest of the demonstration, we will stick with our original object with a two-tailed test to see how we can interpret inconclusive results. In the original study, the pain group scored significantly higher than the control group, but the p-value was .048, so hardly convincing evidence. With Bayes factors, at least we can see we ideally need more data to make a decision.
4.4.1.3 Parameter estimation
We will spend more time on this process in week/chapter 10, but a Bayes factor on its own is normally not enough. We also want an estimate of the effect size and the precision around it. Within the BayesFactor package, there is a function to sample from the posterior distribution using MCMC sampling. We need to pass the t-test object into the posterior function, and include the number of iterations we want. We will use 10,000 here. Depending on your computer, this may take a few seconds.
If you use a one-tailed test, you must index the first object (e.g., Bastian_ttest[1] ) as a one-tailed test includes two lines: 1) the directional alternative we state against the null and 2) the complement of the alternative against the null.
Once we have the samples, we can use the base plot function to see trace plots (more on those in chapter 10) and a density plot of the posterior distributions for several parameters.

The second and fourth plots are what we are mainly interested in for a t-test. Once we know what kind of evidence we have for different hypotheses, typically we want to know what the effect size is. In the BayesFactor package, we get the mean difference between groups (unhelpfully named beta) and the effect size Delta, which is kind of like Cohen's d. It is calculated by dividing the t statistic by the square root of the sample size, so a type of standardised mean difference. One of my main complaints with the BayesFactor package is not explaining what the outputs mean as the only explanation I could find is old blog post with no clear overview in the documentation.
The plot provides the posterior distribution of different statistics based on sampling 10,000 times. For beta, we can see the peak of the distribution is around -0.5, spanning from above 0 to -1. For delta, we can see the peak of the distribution is around -0.5, and spans from above 0 to -1 again.
For a more fine-tuned description of the posterior distribution, we can use handy functions from the bayestestR package ( Makowski et al., 2019 ) . We will use this much more in chapter 10 as there are some great plotting functions, but these functions work for BayesFactor objects. To get the point estimates of each parameter, we can use the point_estimate function:
| Parameter | Median | Mean | MAP |
|---|---|---|---|
| mu | 3.4261304 | 3.4262019 | 3.4131426 |
| beta (Control - Pain) | -0.4848002 | -0.4892667 | -0.4665795 |
| sig2 | 1.1061817 | 1.1348647 | 1.0803148 |
| delta | -0.4619808 | -0.4664735 | -0.4443186 |
| g | 0.5448393 | 7.6797358 | 0.0236393 |
Our best guess (median of the posterior) for the mean difference between groups is -0.49 and a delta of -0.47 in favour of the pain group.
We do not just want a point estimate though, we also want the credible interval around it. For this, we have the hdi function.
| Parameter | CI | CI_low | CI_high |
|---|---|---|---|
| mu | 0.95 | 3.1355925 | 3.7088678 |
| beta (Control - Pain) | 0.95 | -1.0362104 | 0.0505082 |
| sig2 | 0.95 | 0.7316134 | 1.5957396 |
| delta | 0.95 | -0.9816252 | 0.0549678 |
| g | 0.95 | 0.0321040 | 7.7710573 |
So, 95% of the posterior distribution for the mean difference is between -1.04 and 0.04, and that delta is between -0.99 and 0.04. As both values cross 0, we would not be confident in these findings and ideally we would need to collect more data, which is consistent with the Bayes Factor results.
Finally, instead of separate functions, there is a handy wrapper for the median, 95% credible interval, and ROPE (more on that later).
| Parameter | Median | CI | CI_low | CI_high | pd | ROPE_CI | ROPE_low | ROPE_high | ROPE_Percentage | |
|---|---|---|---|---|---|---|---|---|---|---|
| 4 | mu | 3.4261304 | 0.95 | 3.1373459 | 3.7109673 | 1.00000 | 0.95 | -0.1 | 0.1 | 0.0000000 |
| 1 | beta (Control - Pain) | -0.4848002 | 0.95 | -1.0426880 | 0.0452834 | 0.96438 | 0.95 | -0.1 | 0.1 | 0.0540526 |
| 5 | sig2 | 1.1061817 | 0.95 | 0.7707757 | 1.6676312 | 1.00000 | 0.95 | -0.1 | 0.1 | 0.0000000 |
| 2 | delta | -0.4619808 | 0.95 | -0.9985058 | 0.0413485 | 0.96438 | 0.95 | -0.1 | 0.1 | 0.0585263 |
| 3 | g | 0.5448393 | 0.95 | 0.0928315 | 15.8435212 | 1.00000 | 0.95 | -0.1 | 0.1 | 0.0076000 |
There are a bunch of tests and tricks we have not covered here, so check out the Bayesfactor package page online for a series of vignettes.
4.4.1.4 Reporting your findings
When reporting your findings, Doorn et al. ( 2021 ) suggest several key pieces of information to provide your reader:
A complete description and justification of your prior;
Clearly state each hypothesis you are comparing and specify using the Bayes factor notation ( \(BF\) \(_0\) \(_1\) or \(BF\) \(_1\) \(_0\) );
The Bayes factor value and error percentage;
A robustness check of your findings under different plausible priors;
Your parameter estimate (effect size) including the posterior mean or median and its 95% credible / highest density interval (HDI).
Where possible, try and provide the reader with the results in graphical and numerical form, such as including a plot of the posterior distribution. This will be easier in the next chapter as some of the plotting helper functions do not work nicely with the BayesFactor package.
4.4.2 Independent activity (Schroeder & Epley, 2015)
For an independent activity, we will use data from Schroeder & Epley ( 2015 ) . The aim of the study was to investigate whether delivering a short speech to a potential employer would be more effective at landing you a job than writing the speech down and the employer reading it themselves. Thirty-nine professional recruiters were randomly assigned to receive a job application speech as either a transcript for them to read, or an audio recording of the applicant reading the speech.
The recruiters then rated the applicants on perceived intellect, their impression of the applicant, and whether they would recommend hiring the candidate. All ratings were originally on a Likert scale ranging from 0 (low intellect, impression etc.) to 10 (high impression, recommendation etc.), with the final value representing the mean across several items.
For this example, we will focus on the hire rating (variable "Hire_Rating" to see whether the audio condition would lead to higher ratings than the transcript condition (variable "CONDITION" ).
From here, apply what you learnt in the first guided example to this new independent task and complete the questions below to check your understanding. Since we expect higher ratings for audio than transcript, use a one-tailed test. Remember to sample from the posterior, so we can also get estimates of the effect sizes.
You can check your attempt to the solutions at the bottom of the page .
Rounding to two decimals, what is the Bayes Factor in favour of the alternative hypothesis?
Looking at the guidelines from Wagenmakers et al. (2015), how could you describe the evidence in favour of the alternative hypothesis? No Anecdotal Substantial Strong
Rounding to two decimals, what is the absolute (ignoring the sign) mean difference (beta) in favour of the audio condition?
Looking at the 95% credible interval, can we rule out an effect of 0 given these data and model? Yes No
4.5 Bayes factors for two dependent samples
4.5.1 guided example (mehr et al., 2016).
For a paired samples t-test, the process is identical to the independent samples t-test apart from defining the variables. So, we will demonstrate a full example like before with less commentary, then you have an independent data frame to test your understanding.
The next study we are going to look at is by Mehr et al. ( 2016 ) . They were interested in whether singing to infants conveyed important information about social affiliation. Infants become familiar with melodies that are repeated in their specific culture. The authors were interested in whether a novel person (someone they had never seen before) could signal to the child that they are a member of the same social group and attract their attention by singing a familiar song to them.
Mehr et al. (2016) invited 32 infants and their parents to participate in a repeated measures experiment. First, the parents were asked to repeatedly sing a previously unfamiliar song to the infants for two weeks. When they returned to the lab, they measured the baseline gaze (where they were looking) of the infants towards two unfamiliar people on a screen who were just silently smiling at them. This was measured as the proportion of time looking at the individual who would later sing the familiar song (0.5 would indicate half the time was spent looking at the familiar singer. Values closer to one indicate looking at them for longer). The two silent people on the screen then took it in turns to sing a lullaby. One of the people sung the song that the infant’s parents had been told to sing for the previous two weeks, and the other one sang a song with the same lyrics and rhythm, but with a different melody. Mehr et al. (2016) then repeated the gaze procedure to the two people at the start of the experiment to provide a second measure of gaze as a proportion of looking at the familiar singer.
We are interested in whether the infants increased the proportion of time spent looking at the singer who sang the familiar song after they sang, in comparison to before they sang to the infants. We have one dependent variable (gaze proportion) and one within-subjects independent variable (baseline vs test). We want to know whether gaze proportion was higher at test ( "Test_Proportion_Gaze_to_Singer" ) than it was at baseline ( "Baseline_Proportion_Gaze_to_Singer" ).
Like Bastian et al. (2014), we have just anecdotal evidence in favour of the experimental hypothesis over the null ( \(BF\) \(_1\) \(0\) = 2.30).
Mehr et al. (2016) expected gaze proportion to be higher at test, so try defining a one-tailed test and see what kind of evidence we have in favour of the alternative hypothesis.
As before, we know there is only anecdotal evidence in favour of the experimental hypothesis, but we also want the effect size and its 95% credible interval. So, we can sample from the posterior, plot it, and get some estimates.
Just note in the plot we have fewer panels as the paired samples approach simplifies things. Mu is our mean difference in the first panel and delta is our standardised effect in the third panel. For a dependent variable like gaze proportion, an unstandardised effect size is informative and comparable across studies, but its also useful to report standardised effect sizes for future power analyses etc.

We finally have our wrapper function for the median posterior distribution and its 95% credible interval.
| Parameter | Median | CI | CI_low | CI_high | pd | ROPE_CI | ROPE_low | ROPE_high | ROPE_Percentage | |
|---|---|---|---|---|---|---|---|---|---|---|
| 3 | mu | -0.0665270 | 0.95 | -0.1260660 | -0.0079075 | 0.9866 | 0.95 | -0.1 | 0.1 | 0.8898737 |
| 4 | sig2 | 0.0288372 | 0.95 | 0.0182590 | 0.0492998 | 1.0000 | 0.95 | -0.1 | 0.1 | 1.0000000 |
| 1 | delta | -0.3926439 | 0.95 | -0.7480745 | -0.0438846 | 0.9866 | 0.95 | -0.1 | 0.1 | 0.0260000 |
| 2 | g | 0.4905500 | 0.95 | 0.0877182 | 13.6082978 | 1.0000 | 0.95 | -0.1 | 0.1 | 0.0140421 |
We can see here the median posterior estimate of the mean difference is -.07 with a 95% credible interval ranging from -.13 to -.01. As the dependent variable is measured as a proportion of gaze time, infants looked at the familiar singer for 7% (1-13% for the 95% credible interval) longer at test than at baseline. This means we can exclude 0 from the likely effects, but we still only have anecdotal evidence in favour of the experimental hypothesis compared to the null.
4.5.2 Independent activity (Zwaan et al., 2020)
For your final independent activity, we have data from Zwaan et al. ( 2018 ) who wanted to see how replicable experiments from cognitive psychology are. For this exercise, we will explore the flanker task .
In short, we have two conditions: congruent and incongruent. In congruent trials, five symbols like arrows are the same and participants must identify the central symbol with a keyboard response. In incongruent trials, the four outer symbols are different to the central symbol. Typically, we find participants respond faster to congruent trials than incongruent trials. The dependent variable here is the mean response time in milliseconds (ms).
We want to know whether response times are faster to congruent trials ( "session1_responsecongruent" ) than incongruent trials ( "session1_incongruent" ). Zwaan et al. measured a few things like changing the stimuli and repeating the task in two sessions, so we will just focus on the first session for this example.
Perform a paired samples t-test comparing the response times to congruent and incongruent trials. The questions below relate to a one-tailed test since there is a strong prediction to expect faster responses in the congruent condition compared to the incongruent condition. Think carefully about whether you expect positive or negative effects depending on the order you enter the variables.
- Looking at the guidelines from Wagenmakers et al. (2011), how could you describe the evidence in favour of the alternative hypothesis? Substantial Strong Very strong Extreme
The Bayes Factor for this analysis is huge. Unless you edit the settings, R reports large numbers in scientific notation. The Bayes Factor in favour of the alternative hypothesis here is 8.7861e+12 or as a real number 8786100000000. For a finding as established as the flanker task, testing against a point null is not too informative, but this shows what extreme evidence looks like. We will come back to this in the ROPE demonstration later.
Rounding to two decimals, what is the absolute (ignoring the sign) mean difference (beta) in response time between congruent and incongruent trials?
Looking at the 95% credible interval for mu, we would expect the absolute mean difference to range between 30.06 38.78 47.54 ms and 30.06 38.78 47.54 ms.
Rounding to two decimals, what is the absolute standardised mean difference (delta) in response time between congruent and incongruent trials?
4.6 Equivalence Testing vs ROPE
4.6.1 guided example for two independent samples (bastian et al., 2014).
In sections 9.4 and 9.5, we focused on the Bayesian approach to null hypothesis testing. We compared the alternative hypothesis to the null hypothesis and wanted to know how much we should shift our beliefs. However, there are times when comparing against a point null is uninformative. The same advice applies to frequentist statistics where you can use equivalence testing (see the bonus section in the appendix if you are interested in this). In this setup, you set two boundaries representing your smallest effect size of interest (SESOI) and conduct a two one-sided test: one comparing your sample mean (difference) to the upper bound and one comparing your sample mean (difference) to the lower bound. If both tests are significant, you can conclude the mean was within your bounds and it is practically equivalent to zero.
In a Bayesian framework, we follow a similar approach by setting an upper and lower bound for the interval we consider practically or theoretically meaningful. This is known as the Region of Practical Equivalence (ROPE). However, we do not perform a two one-sided test, we directly compare the posterior distribution to the ROPE and interpret how much of the ROPE captures our 95% credible interval. This creates three decisions ( Kruschke & Liddell, 2018a ) instead of comparing the experimental hypothesis to the point null:
HDI completely outside the ROPE: We reject the ROPE as the parameter is larger than the effects we consider too small to be practically/theoretically meaningful.
HDI completely within the ROPE: We accept the ROPE as the parameter is smaller than the effects we consider practically/theoretically meaningful.
HDI and the ROPE partially overlap: We are undecided as we need more data and greater precision in the posterior to make a decision about whether we can reject the ROPE.
This will be more meaningful in chapter 10 when we turn to Bayesian modelling as the bayestestR package has great functions for visualising the ROPE, but they unfortunately do not work with BayesFactor objects. We will return to the Bastian et al. (2014) data and the describe_posterior ( ) function. If you explored the complete output earlier, you might have noticed the values relating to ROPE, but we ignored it at the time. As a reminder, lets see the output:
For more information on ROPE within the bayestestR package, see the online vignettes . In the output, we have:
The 95% credible interval - we will need this to compare to the ROPE.
The probability of direction (pd) - how much of the posterior distribution is in a positive or negative direction?
Region of practical equivalence (ROPE) - the interval we would consider for our SESOI.
% in ROPE - how much of the posterior is within the ROPE?
By default, the describe_posterior ( ) function sets the ROPE region to the mean plus or minus 0.1 * SD of your response. We can set our own ROPE using the rope_range argument. Justifying your ROPE is probably the most difficult decision you will make as it requires subject knowledge for what you would consider the smallest effect size of interest. From the lecture, there are different strategies:
Your understanding of the applications / mechanisms (e.g., a clinically meaningful decrease in pain).
Smallest effects from previous research (e.g., lower bound of individual study effect sizes or lower bound of a meta-analysis).
Small telescopes (the effect size the original study had 33% power to detect).
For Bastian et al. (2014), they measured bonding on a 5-point Likert scale, so we might consider anything less than a one-point difference as too small to be practically meaningful.
| Parameter | Median | CI | CI_low | CI_high | pd | ROPE_CI | ROPE_low | ROPE_high | ROPE_Percentage | |
|---|---|---|---|---|---|---|---|---|---|---|
| 4 | mu | 3.4261304 | 0.95 | 3.1373459 | 3.7109673 | 1.00000 | 0.95 | -1 | 1 | 0.0000000 |
| 1 | beta (Control - Pain) | -0.4848002 | 0.95 | -1.0426880 | 0.0452834 | 0.96438 | 0.95 | -1 | 1 | 0.9898737 |
| 5 | sig2 | 1.1061817 | 0.95 | 0.7707757 | 1.6676312 | 1.00000 | 0.95 | -1 | 1 | 0.2915789 |
| 2 | delta | -0.4619808 | 0.95 | -0.9985058 | 0.0413485 | 0.96438 | 0.95 | -1 | 1 | 1.0000000 |
| 3 | g | 0.5448393 | 0.95 | 0.0928315 | 15.8435212 | 1.00000 | 0.95 | -1 | 1 | 0.6907789 |
Note how changing the ROPE range changes the values for every parameter, so you will need to think which parameter you are interested in and what would be a justifiable ROPE for it. For this example, we will focus on the mean difference between groups (beta). Using a ROPE of plus or minus 1, 99.26% of the 95% HDI is within the ROPE. Its so close, but it falls in the third decision from above where we need more data to make a decision. The lower bound of the HDI is -1.03, so it extends just outside our ROPE region.
Compared to the standard Bayes factor where we had weak evidence in favour of the alternative hypothesis compared to the point null, using the ROPE approach means we also have an inconclusive decision, but our effect size is almost too small to be practically meaningful.

4.6.2 Independent activity for two independent samples (Schroeder & Epley, 2014)
For this activity, you will need the objects you created in section 9.4.2 for the independent activity. Remember it is based on a one-tailed t-test as we expected higher ratings for the audio group compared to the transcript group. You will need the samples from the posterior as the only thing you will need to change is the arguments you use in the describe_posterior ( ) function.
Use the describe_posterior ( ) from section 9.4.2 , but this time enter values for the ROPE arguments. The original study was on a 10-point scale. Your choice of ROPE will depend on your understanding of the subject area, but they measured their outcomes on a 0-10 scale. We might have a higher bar for concluding a meaningful effect of medium on people's hire ratings, so use a ROPE region of 2 points. Since we used a one-tailed test focusing on negative effects (transcript < audio), we can just focus on the region between -2 and 0.
Looking at the 95% credible interval for beta, we would expect the absolute mean difference to range between 0.32 2.94 3.11 4.52 and 0.32 2.94 3.11 4.52 .
Rounding to two decimals, what percentage of the 95% credible interval is within the ROPE?
What is the most appropriate conclusion based on this ROPE?:
4.6.3 Guided example for two dependent samples (Mehr et al., 2014)
For the Mehr et al. (2014) data, the outcome is a little easier to interpret for an unstandardised effect than the two between-subjects examples. They compared infants' proportion of gaze duration spent on the model that sang the familiar song and wanted to know whether this would increase at test compared to baseline. As the proportion of gaze is bound between 0 (none of the time) to 1 (all of the time), we might consider a 5% (0.05) increase or decrease as theoretically meaningful if we are not very certain the test will be higher than baseline.
| Parameter | Median | CI | CI_low | CI_high | pd | ROPE_CI | ROPE_low | ROPE_high | ROPE_Percentage | |
|---|---|---|---|---|---|---|---|---|---|---|
| 3 | mu | -0.0665270 | 0.95 | -0.1260660 | -0.0079075 | 0.9866 | 0.95 | -0.05 | 0.05 | 0.2747263 |
| 4 | sig2 | 0.0288372 | 0.95 | 0.0182590 | 0.0492998 | 1.0000 | 0.95 | -0.05 | 0.05 | 1.0000000 |
| 1 | delta | -0.3926439 | 0.95 | -0.7480745 | -0.0438846 | 0.9866 | 0.95 | -0.05 | 0.05 | 0.0022842 |
| 2 | g | 0.4905500 | 0.95 | 0.0877182 | 13.6082978 | 1.0000 | 0.95 | -0.05 | 0.05 | 0.0000000 |
Our observed mean difference was a posterior median of -0.07, 95% CI = [-.13, -0.01], which is 27.50% within the ROPE region of plus or minus 0.05 points. We are not far off ruling out our ROPE, but we still need more data to make a decision. Hopefully, you can see by this point, many of these studies have more inconclusive conclusions when analysed through a Bayesian framework than the original frequentist statistics.
4.6.4 Independent activity for two dependent samples (Zwaan et al., 2018)
For this activity, you will need the objects you created in section 9.5.2 for the independent activity. Remember it is based on a one-tailed t-test as we expected faster response times to congruent trials than incongruent trials. You will need the samples from the posterior as the only thing you will need to change is the arguments you use in the describe_posterior ( ) function.
Use the describe_posterior ( ) from section 9.5.2 , but this time enter values for the ROPE arguments. Set your ROPE to -10-0ms (or 0-10 depending on the order you entered the variables) as these are smaller effects closer to the sampling error we can expect with response time experiments held online ( Reimers & Stewart, 2015 ) .
Looking at the 95% credible interval for mu, we would expect the absolute mean difference to range between 30.06 31.48 38.78 47.54 and 30.06 31.48 38.78 47.54 .
What percentage of the 95% credible interval is within the ROPE?
4.7 Summary
In this chapter, you learnt about hypothesis testing using a Bayesian framework. The first two activities explored the logic of Bayesian statistics to make inferences and how it can be used to test hypotheses when expressed as the Bayes factor. You then learnt how to perform Bayes factors applied to the simplest cases of two independent samples and two dependent samples. Bayes factors are a useful way of quantifying the evidence in favour of a hypotheses compared to a competing hypothesis. Bayesian statistics can still be used mindlessly, but hopefully you can see they provide the opportunity to move away from purely dichotomous thinking. Evidence that would be statistically significant ( p < .05) but close to alpha only represents anecdotal evidence.
As with any new skill, practice is the best approach to becoming comfortable in applying your knowledge to novel scenario. Hopefully, you worked through the guided examples and tested your understanding on the independent activities.
For further learning, we recommend the following resources relevant to this chapter:
Doorn et al. ( 2021 ) - Although it focuses on the JASP software, this article provides an accessible introduction to Bayes factors and how you can report your findings.
Kruschke & Liddell ( 2018b ) - This article discusses the proposed shift away from dichotomous hypothesis testing towards estimation and how it relates to Bayesian statistics through summarising the posterior and the ROPE procedure.
Wong et al. ( 2021 ) - Although Bayes factors have the potential to help you make more nuanced inferences, they are still prone to misinterpretations. This preprint outlines common errors and misconceptions when researcher report Bayes factors.
4.8 Independent activity solutions
4.8.1 schroeder and epley (2015) bayes factor.

| Parameter | Median | CI | CI_low | CI_high | pd | ROPE_CI | ROPE_low | ROPE_high | ROPE_Percentage | |
|---|---|---|---|---|---|---|---|---|---|---|
| 4 | mu | 3.8130925 | 0.95 | 3.109169 | 4.5185592 | 1 | 0.95 | -0.1 | 0.1 | 0 |
| 1 | beta (Transcript - Audio) | -1.5465217 | 0.95 | -2.946880 | -0.3121002 | 1 | 0.95 | -0.1 | 0.1 | 0 |
| 5 | sig2 | 4.7849364 | 0.95 | 3.138439 | 7.8110282 | 1 | 0.95 | -0.1 | 0.1 | 0 |
| 2 | delta | -0.7084995 | 0.95 | -1.362898 | -0.1365876 | 1 | 0.95 | -0.1 | 0.1 | 0 |
| 3 | g | 0.7529274 | 0.95 | 0.113435 | 21.8814934 | 1 | 0.95 | -0.1 | 0.1 | 0 |
4.8.2 Zwaan et al. (2020) Bayes factor

| Parameter | Median | CI | CI_low | CI_high | pd | ROPE_CI | ROPE_low | ROPE_high | ROPE_Percentage | |
|---|---|---|---|---|---|---|---|---|---|---|
| 3 | mu | -38.7918762 | 0.95 | -47.6011164 | -30.0234377 | 1 | 0.95 | -0.1 | 0.1 | 0 |
| 4 | sig2 | 3146.1775444 | 0.95 | 2548.8931250 | 3953.1759593 | 1 | 0.95 | -0.1 | 0.1 | 0 |
| 1 | delta | -0.6923077 | 0.95 | -0.8652760 | -0.5196815 | 1 | 0.95 | -0.1 | 0.1 | 0 |
| 2 | g | 0.7060218 | 0.95 | 0.1296344 | 19.6262419 | 1 | 0.95 | -0.1 | 0.1 | 0 |
4.8.3 Schroeder and Epley (2015) ROPE
| Parameter | Median | CI | CI_low | CI_high | pd | ROPE_CI | ROPE_low | ROPE_high | ROPE_Percentage | |
|---|---|---|---|---|---|---|---|---|---|---|
| 4 | mu | 3.8130925 | 0.95 | 3.109169 | 4.5185592 | 1 | 0.95 | -2 | 0 | 0.0000000 |
| 1 | beta (Transcript - Audio) | -1.5465217 | 0.95 | -2.946880 | -0.3121002 | 1 | 0.95 | -2 | 0 | 0.7561895 |
| 5 | sig2 | 4.7849364 | 0.95 | 3.138439 | 7.8110282 | 1 | 0.95 | -2 | 0 | 0.0000000 |
| 2 | delta | -0.7084995 | 0.95 | -1.362898 | -0.1365876 | 1 | 0.95 | -2 | 0 | 1.0000000 |
| 3 | g | 0.7529274 | 0.95 | 0.113435 | 21.8814934 | 1 | 0.95 | -2 | 0 | 0.0000000 |
4.8.4 Zwaan et al. (2020) ROPE
| Parameter | Median | CI | CI_low | CI_high | pd | ROPE_CI | ROPE_low | ROPE_high | ROPE_Percentage | |
|---|---|---|---|---|---|---|---|---|---|---|
| 3 | mu | -38.7918762 | 0.95 | -47.6011164 | -30.0234377 | 1 | 0.95 | -10 | 0 | 0 |
| 4 | sig2 | 3146.1775444 | 0.95 | 2548.8931250 | 3953.1759593 | 1 | 0.95 | -10 | 0 | 0 |
| 1 | delta | -0.6923077 | 0.95 | -0.8652760 | -0.5196815 | 1 | 0.95 | -10 | 0 | 1 |
| 2 | g | 0.7060218 | 0.95 | 0.1296344 | 19.6262419 | 1 | 0.95 | -10 | 0 | 0 |
An official website of the United States government
The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.
The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.
- Publications
- Account settings
Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .
- Advanced Search
- Journal List
- Entropy (Basel)

A Review of Bayesian Hypothesis Testing and Its Practical Implementations
Associated data.
The sleep and the ToothGrowth datasets are built in R. The Poisson repeated-measures dataset is simulated according to Appendix A .
We discuss hypothesis testing and compare different theories in light of observed or experimental data as fundamental endeavors in the sciences. Issues associated with the p -value approach and null hypothesis significance testing are reviewed, and the Bayesian alternative based on the Bayes factor is introduced, along with a review of computational methods and sensitivity related to prior distributions. We demonstrate how Bayesian testing can be practically implemented in several examples, such as the t -test, two-sample comparisons, linear mixed models, and Poisson mixed models by using existing software. Caveats and potential problems associated with Bayesian testing are also discussed. We aim to inform researchers in the many fields where Bayesian testing is not in common use of a well-developed alternative to null hypothesis significance testing and to demonstrate its standard implementation.
1. Introduction
Hypothesis testing is an important tool in modern research. It is applied in a wide range of fields, from forensic analysis, business intelligence, and manufacturing quality control, to the theoretical framework of assessing the plausibility of theories in physics, psychology, and fundamental science [ 1 , 2 , 3 , 4 , 5 ]. The task of comparing competing theories based on data is essential to scientific activity, and therefore, the mechanism of conducting these comparisons requires thoughtful consideration [ 6 , 7 ].
The dominant approach for these comparisons is based on hypothesis testing using a p -value, which is the probability, under repeated sampling, of obtaining a test statistic at least as extreme as the observed under the null hypothesis [ 4 , 8 ]. Records of conceptualizing the p -value date back at least two hundred years before Ronald Fisher established the p -value terminology and technique [ 9 , 10 , 11 ]. These records are an indication of how compelling and popular the approach is, and the long history explains the widespread acceptance of a decision rule with a fixed type I error rate, which further resulted in the adoption of a 5% significance-level cutoff. Despite its prevalence, there has been an intense debate about the misuse of the p -value approach [ 7 , 12 ]. The major criticisms about the p -value are its inability to quantify evidence for the null hypothesis and its tendency to overestimate the evidence against the null hypothesis [ 4 ]. For example, a possible decision based on the p -value is the rejection of the null hypothesis but not its acceptance. Under the null hypothesis, the p -value will have a uniform [0, 1] distribution regardless of the sample size. This is by construction. The Bayesian approach behaves rather differently under the null hypothesis, and increasing sample sizes will provide increasing degrees of evidence in favor of the null hypothesis [ 13 ].
Besides the misuse, the hypothesis testing approach based on the p -value can be easily misinterpreted. A list of twenty-five examples of misinterpretations in classical hypothesis testing is provided in [ 14 ]. Eighteen of these items are directly related to the misunderstanding of the p -value, and the others are related to p -values in the context of confidence intervals and statistical power. Some of these points are also shared in [ 15 ], including the common misconceptions that a nonsignificant difference means that there is no difference between groups and that the p -value represents the chance of a type I error. The author also highlights an alternative approach, based on the Bayes factor as a measure of true evidential meaning about the hypotheses [ 16 , 17 ]. Private pages of Alan Turing independently discovered this quantity around the same time as Jeffrey [ 16 , 18 , 19 ]. Other authors have also recommended the Bayes factor as a better solution to hypothesis testing compared with the practice of p -values and null hypothesis significance testing (NHST), specifically criticizing the p -value’s dependence on hypothetical data, which are likely to be manipulated by the researcher’s intentions [ 8 ].
While the majority of the issues with classical hypothesis testing are crucial and widely known, a less acknowledged but important misinterpretation happens when two or more results are compared by their degrees of statistical significance [ 20 ]. To illustrate this issue, consider the following example introduced in [ 14 ]. Suppose two independent studies have effect estimates and standard errors of 25 ± 10 and 10 ± 10 . In that case, the first study has a mean that is 2.5 standard errors away from 0, being statistically significant at an alpha level of 1%. The second study has a mean that is 1 standard error away from 0 and is not statistically significant at the same alpha level. It is tempting to conclude that the results of the studies are very different. However, the estimated difference in treatment effects is 25 − 10 = 15 , with a standard error 10 2 + 10 2 ≈ 14 . Thus, the mean of 15 units is less than 1 standard error away from 0, indicating that the difference between the studies is not statistically significant. If a third independent study with a much larger sample size had an effect estimate of 2.5 ± 1.0 , then it would have a mean that is 2.5 standard errors away from 0 and indicate statistical significance at an alpha level of 1%, as in the first study. In this case, the difference between the results of the third and the first studies would be 22.5 with a standard error 10 2 + 1 ≈ 10 . Thus, the mean of 22.5 units would be more than 2 standard errors away from 0, indicating a statistically significant difference between the studies. Therefore, the researchers in [ 20 ] recommend that the statistical significance of the difference between means be considered, rather than the difference between the significance levels of the two hypotheses.
To prevent the misuse and misinterpretation of p -values, the American Statistical Association (ASA) issued a statement clarifying six principles for the proper use and interpretation of classical significance testing [ 12 ]: (i) p -values can indicate how incompatible the data are with a specified statistical model; (ii) p -values do not measure the probability that the studied hypothesis is true, or the probability that the data were produced by random chance alone; (iii) scientific conclusions and business or policy decisions should not be based only on whether a p -value passes a specific threshold; (iv) proper inference requires full reporting and transparency; (v) p -value, or statistical significance, does not measure the size of an effect or the importance of a result; and (vi) by itself, a p -value does not provide a good measure of evidence regarding a model or hypothesis.
The profound criticism of the p -value approach has promoted the consideration and development of alternative methods for hypothesis testing [ 4 , 8 , 12 , 21 ]. The Bayes factor is one such instance [ 18 , 22 ], since it only depends on the observed data and allows an evaluation of the evidence in favor of the null hypothesis. The seminal paper by Kass and Raftery [ 17 ] discusses the Bayes factor along with technical and computational aspects and presents several applications in which the Bayes factor can solve problems that cannot be addressed by the p -value approach. Our review differs in that it is targeted towards researchers in fields where the p -value is still in dominant use, and there are many such fields where this is the case. Our emphasis is to provide these researchers with an understanding of the methodology and potential issues, and a review of the existing tools to implement the Bayes factor in statistical practice.
Two potential issues for the implementation of the Bayes factor are the computation of integrals related to the marginal probabilities that are required to evaluate them and the subjectivity regarding the choosing of the prior distributions [ 7 , 17 ]. We will review these issues in Section 2 and Section 3 , respectively. Despite these difficulties, there are many advantages to the use of the Bayes factor, including (i) the quantification of the evidence in favor of the null hypothesis [ 15 ], (ii) the ease of combining Bayes factors across experiments, (iii) the possibility of updating results when new data are available, (iv) interpretable model comparisons, and (v) the availability of open-source tools to compute Bayes factors in a variety of practical applications.
This paper aims to provide examples of practical implementations of the Bayes factor in different scenarios, highlighting the availability of tools for its computation for those with a basic understanding of statistics. In addition, we bring attention to the over-reliance on the classical p -value approach for hypothesis testing and its inherent pitfalls. The remainder of the article is structured as follows. In Section 2 , we define the Bayes factor and discuss technical aspects, including its numerical computation. In Section 3 , we discuss prior distributions and the sensitivity of the Bayes factor to prior distributions. Section 4 presents several applications of the Bayes factor using open-source code involving R software. We illustrate the computation of the Bayes factor using a variety of approximation techniques. Section 5 presents a discussion and summary.
2. Bayes Factor Definition and Technical Aspects
2.1. definition.
The Bayes factor is defined as the ratio of the probability of the observed data , conditional on two competing hypotheses or models. Given the same data D and two hypotheses H 0 and H 1 , it is defined as
If there is no previous knowledge in favor of one theory over the other, i.e., the hypotheses H 0 and H 1 are equally probable a priori ( p ( H 1 ) = p ( H 0 ) ), the Bayes factor represents the ratio of the data-updated knowledge about the hypotheses, i.e., the Bayes factor is equal to the posterior odds, where the posterior probability is defined as the conditional probability of the hypothesis given the data. Using the definition of conditional probability and under the assumption that the hypotheses are equally probable a priori,
Based on Equation ( 2 ), we can interpret the Bayes factor as the extent to which the data update the prior odds, and therefore, quantify the support for one model over another. A Bayes factor value smaller than one indicates that the data are more likely under the denominator model than they are under the numerator model. A model with the highest Bayes factor shows the relatively highest amount of evidence in favor of the model compared to the other models. Similarly, by switching the indices in ( 1 ), B F 01 is defined as
where larger values of B F 01 represent higher evidence in favor of the null hypothesis.
The Bayes factor can be viewed as a summary of the evidence given by data in support of one hypothesis in contrast to another [ 7 , 17 ]. Reporting Bayes factors can be guided by setting customized thresholds according to particular applications. For example, Evett [ 1 ] argued that for forensic evidence alone to be conclusive in a criminal trial, it would require a Bayes factor of at least 1000 rather than the value of 100 suggested by the Jeffreys scale of interpretation [ 18 ]. A generally accepted table provided in [ 17 ] is replicated in Table 1 , and other similar tables are available in [ 21 ]. Thus, using the Bayes factor can result in reporting evidence in favor of the alternative hypothesis, evidence in favor of the null hypothesis, or reporting that the data are inconclusive.
General-purpose interpretation of Bayes factor values from [ 17 ].
| Interpretation of Evidence against | |
|---|---|
| 1 to 3 | Not worth more than a bare mention |
| 3 to 20 | Positive |
| 20 to 150 | Strong |
| >150 | Very Strong |
The Bayes factor can avoid the drawbacks associated with p -values and assess the strength of evidence in favor of the null model along with various additional advantages. First, Bayes factors inherently include a penalty for complex models to prevent overfitting. Such a penalty is implicit in the integration over parameters required to obtain marginal likelihoods. Second, the Bayes factor can be applied in statistical settings that do not satisfy common regularity conditions [ 17 ].
Despite its apparent advantages, there are a few disadvantages to the Bayes factor approach. First, the choice of a prior distribution is subjective [ 4 , 7 , 17 ] and might be a concern for some researchers. However, the authors in [ 7 ] challenge the criticism, claiming that there is nothing about the data, by itself, that assures it counts as evidence. The pathway from the data to evidence is filled with subjective evaluations when combing the theoretical viewpoint with the research question. Therefore, the Bayesian approach makes explicit assumptions based on the prior likelihood statement. A way to avoid the explicit selection of prior densities is through the use of the Bayesian information criterion (BIC), which can give a rough interpretation of evidence in Table 1 .
Another potential disadvantage is the computational difficulty of evaluating marginal likelihoods, and this is discussed in Section 2.2 . However, the issue is being mitigated by the growth of computational power and the availability of open-source statistical tools for this computation. Examples of these tools are BayesFactor , brms , and BFpack R packages [ 23 , 24 , 25 ]; and JASP [ 26 ] software. In Section 4 , we illustrate the required R scripting for a number of examples widely used in data analysis. As Python has become increasingly popular among quantitative practitioners [ 27 , 28 ], R packages for the computation of Bayes factors can be imported into Python using the rpy2 package [ 29 ]. Thanks to these advancements, Bayes factors are gradually gaining wider attention in research [ 30 , 31 , 32 ].
2.2. Computation of the Bayes Factor
To calculate the Bayes factor, both the numerator and the denominator in the Bayes factor definition ( 1 ) (the marginal likelihood of the data under a given model) involve integrals over the parameter space:
where θ k is the parameter vector under the hypothesis H k , and p ( θ k | H k ) is the prior probability density function of the parameter vector for the hypothesis H k . It is typical for ( 4 ) to be an integral over many dimensions so that the computational problem can be difficult.
If we assume the data are a random sample from an exponential family distribution and assume conjugate priors, it is possible to solve the integral in ( 4 ) analytically. Without conjugacy, these integrals are often intractable, and numerical methods are needed. Many available numerical integration techniques are inefficient to calculate such integrals because it is difficult to find the regions where the probability mass is accumulating in higher dimensions. For regular problems in the large sample setting, the probability mass will accumulate and tend to peak around the maximum likelihood estimator (MLE) [ 17 , 33 ]. This notion underlies the Laplace approximation and its variations which can be used to obtain an approximation to the Bayes factor. These methods rely on a quadratic approximation to the logarithm of the integrand obtained using a Taylor expansion about the MLE and a normal distribution matching. Laplace’s methods are usually fast but not very accurate. An alternative approximation known as the Savage–Dickey density ratio [ 34 ] can be applied to obtain a better approximation for the case of nested models when testing a constrained model against an unrestricted alternative, the Bayes factor is approximated by dividing the value of the posterior density over the parameters for the alternative model evaluated at the hypothesized value, by the prior for the same model evaluated at the same point [ 35 ].
For the general case of Bayes factor computations, it is common to resort to sampling-based numerical procedures adjusted to the context of marginal likelihood computation as in ( 4 ). Evans and Swartz [ 36 ] reviewed several numerical strategies for assessing the integral related to the Bayes factor and later published a book on the topic [ 37 ]. Among the methods for estimating the integral of the marginal likelihood, the bridge sampling technique has gained prominence [ 38 ]. The method encompasses three special cases, namely the “naïve” [ 33 ] or “simple” [ 17 ] Monte Carlo estimator, the importance sampling, and the generalized harmonic mean estimator. The bridge sampling estimate stands out for not being dominated by samples from the tails of the distribution [ 33 ]. An entitled bridgesampling R package to estimate integrals with the bridge sampling algorithm for Bayesian models implemented in Stan [ 39 ] or JAGS [ 40 ] is available [ 41 ]. In Section 4 , we provide examples of using the bridgesampling package and the BayesFactor R package [ 23 ] to enable the computation of Bayes factors for several important experimental designs.
3. Prior Elicitation and Sensitivity Analysis
Based on its definition in ( 1 ), the Bayes factor is a ratio of the marginal likelihood of two competing models. The marginal likelihood for a model class is a weighted average of the likelihood over all the parameter values represented by the prior distribution [ 42 ]. Therefore, carefully choosing priors and conducting a prior sensitivity analysis play an essential role when using Bayes factors as a model selection tool. This section briefly discusses the prior distributions, prior elicitation, and prior sensitivity analysis.
3.1. Prior Distributions
In Bayesian statistical inference, a prior probability distribution (or simply called the prior) estimates the probability of incorporating one’s beliefs or prior knowledge about an uncertain quantity before collecting the data. The unknown quantity may be a parameter of the model or a latent variable. In Bayesian hierarchical models, we have more than one level of prior distribution corresponding to a hierarchical model structure. The parameters of a prior distribution are called hyperparameters. We can either assume values for the hyperparameters or assume a probability distribution, which is referred to as a hyperprior.
It is common to categorize priors into four types: informative priors, weakly informative priors, uninformative priors, and improper priors [ 43 ]. The Bayes factor computation requires proper priors, i.e., a prior distribution that integrates to 1. Various available software provide default priors, but it is the researchers’ responsibility to perform sensitivity analysis to check the impact of applying different priors.
3.2. Prior Elicitation
The prior distribution is an important ingredient of the Bayesian paradigm and must be designed coherently to make Bayesian inference operational [ 44 ]. Priors can be elicited using multiple methods, e.g., from past information, such as previous experiments, or elicited purely from the experts’ subjective assessments. When no prior information is available, an uninformative prior can be assumed, and most of the model information that is given by the posterior will come from the likelihood function itself. Priors can also be chosen according to some principles, such as symmetry or maximum entropy, given constraints. Examples are the Jeffreys prior [ 18 ] and Bernardo’s reference prior [ 45 ]. When a family of conjugate priors exist, choosing a prior from that family simplifies the calculation of the posterior distribution.
With the advancement of computational power, ad hoc searching for priors can be done more systemically. Hartmann et al. [ 46 ] utilized the prior predictive distribution implied by the model to automatically transform experts’ judgments about plausible outcome values to suitable priors on the parameters. They also provided computational strategies to perform inference and guidelines to facilitate practical use. Their methodology can be summarized as follows: (i) define the parametric model for observable data conditional on the parameters θ and a prior distribution with hyperparameters λ for the parameters θ , (ii) obtain experts’ beliefs or probability for each mutually exclusive data category partitioned from the overall data space, (iii) model the elicited probabilities from step 2 as a function of the hyperparameters λ , (iv) perform iterative optimization of the model from step 3 to obtain an estimate for λ best describing the expert opinion within the chosen parametric family of prior distributions, and (v) evaluate how well the predictions obtained from the optimal prior distribution can describe the elicited expert opinion. Prior predictive tools relying on machine learning methods can be useful when dealing with hierarchical modeling where a grid search method is not possible [ 47 ].
3.3. Sensitivity Analysis
In the Bayesian approach, it is important to evaluate the impact of prior assumptions. This is performed through a sensitivity analysis where the prior is perturbed, and the change in the results is examined. Various authors have demonstrated how priors affect Bayes factors and provided ways to address the issue. When comparing two nested models in a low dimensional parameter space, the authors in [ 48 ] propose a point mass prior Bayes factor approach. The point mass prior distribution for the Bayes factor is computed for a grid of extra parameter values introduced by a generalized alternative model. The resulting Bayes factor is obtained by averaging the point mass prior Bayes factor over the prior distribution of the extra parameter(s).
For binomial data, Ref. [ 42 ] shows the impact of different priors on the probability of success. The authors used four different priors: (i) a uniform distribution, (ii) the Jeffreys prior, which is a proper Beta(0.5,0.5) distribution, (iii) the Haldane prior by assuming a Beta(0,0) distribution (an improper prior), and (iv) an informative prior. The uniform, Jeffreys, and Haldane priors are noninformative in some sense. Although the resulting parameter estimation is similar in all four scenarios, the resulting Bayes factor and posterior probability of H 1 vary. Using the four different priors produces very different Bayes factors with values of 0.09 for the Haldane, 0.6 for the Jeffreys, 0.91 for the uniform, and 1.55 for the informative prior. The corresponding posterior probabilities of H 1 are 0.08 (Haldane), 0.38 (Jeffreys), 0.48 (uniform), and 0.61 (informative). In this example, the sensitivity analysis reveals that the effect of the priors on the posterior distribution is different from their effect on the Bayes factor. The authors emphasize that Bayes factors should be calculated, ideally, for a wide range of plausible priors whenever used as a model selection tool. Besides using the Bayes factor based on prior predictive distribution, they also suggest seeking agreement with the other model selection criterion designed to assess local model generalizability (i.e., based on posterior predictive distribution).
The author in [ 49 ] describe several interesting points with regards to prior sensitivity. The author views prior sensitivity analysis in theory testing as an opportunity rather than a burden. They argue that it is an attractive feature of a model evaluation measure when psychological models containing quantitatively instantiated theories are sensitive to priors. Ref. [ 49 ] believes that using an informative prior expressing a psychological theory and evaluating models using prior sensitivity measures can serve to advance knowledge. Finally, sensitivity analysis is accessible through an interactive Shiny Application developed by the authors in [ 50 ]. The software is designed to help user understand how to assess the substantive impact of prior selection in an interactive way.
4. Applications of the Bayes Factor Using R Packages
In this section, we illustrate how to calculate Bayes factors using various techniques available in R, including the R package BayesFactor [ 23 ]. Various authors have used this package to compute Bayes factors in different settings such as linear correlations, Bayesian t -tests, analysis of variance (ANOVA), linear regression, single proportions, and contingency tables [ 51 , 52 , 53 , 54 ]. Comparisons between Bayesian and frequentist approaches are provided in the vignettes of [ 23 ]. We provide the R code to compute the Bayes factor for a one-sample t -test, a multiway ANOVA, a repeated-measures design, and a Poisson generalized linear mixed model (GLM).
4.1. One-Sample t-Test
The authors in [ 52 ] derived the Jeffreys Zellner Siow (JZS) Bayes factor as a function of the t -score and the sample size. To illustrate how the ttestBF function of the BayesFactor package performs a Bayesian paired t -test, they analyzed the sleep dataset [ 55 ], which includes the variable, i.e., the length of increased sleep (in hours) after taking two drugs when compared to regular nights where no drug was administered. The Bayesian paired t -test can evaluate if the levels of effectiveness of two drugs are significantly different (a null hypothesis is that the standardized effect size is zero) [ 7 , 52 ].
Let y 1 , … , y n ∼ i . i . d . N ( σ δ , σ 2 ) , where the standardized effect size is given by δ = μ / σ , μ is a grand mean, and σ 2 is the error variance. We test the following hypotheses:
The following script of R code implements the Bayesian paired t -test and presents the p -value of the classical approach for comparison.

The value r = 0.707 ( 2 / 2 ) denotes the scale of a Cauchy prior distribution of δ . The Bayes factor value of 17.259 favors the alternative hypothesis, indicating that the effect size is significant in this case. Using the interpretation in Table 1 , the evidence against the null hypothesis is “positive”. The classical p -value of around 0.3% is also in favor of the alternative, usually considered strong evidence against the null hypothesis.
For this example, the Bayes factor can also be computed by employing a bridge sampling estimate. The R packages bridgesampling and R2jags used concepts of object-oriented programming and were developed with methods to interact with customizable Markov chain Monte Carlo object routines [ 41 , 56 ]. That is to say, a self-coded in JAGS model can feed the bridgesampling ’s function bridge_sampler to obtain the log marginal likelihood for the model. Their source code (assuming the same priors in [ 23 ]) is available at https://osf.io/3yc8q/ (accessed on 28 December 2021). The Bayes factor value in [ 41 ] for the sleep data is 17.260, which is almost identical to the BayesFactor package result, 17.259. Both the BayesFactor and bridgesampling packages suit the analysis needs. On the one hand, no additional programming knowledge is required to call the functions in the BayesFactor package due to the default prior settings, which are user friendly. On the other hand, the bridgsampling along with JAGS allows for more sophisticated customization and flexibility in model specifications, which makes more feasible to conduct the sensitivity analysis.
4.2. Multiway ANOVA
Consider a two-way ANOVA model M 1 : y i j k = μ + σ ( τ i + β j + γ i j ) + ϵ i j k , for i = 1 , ⋯ , a , j = 1 , ⋯ , b , and k = 1 , ⋯ , n , where y i j k is the response for the k th subject at the i th level of Factor 1 and the j th level of Factor 2, μ is the overall mean effect, τ i is the standardized effect size of the i th level of Factor 1, β j is the standardized effect size of the j th level of Factor 2, γ i j is the standardized effect size of the interaction between two factors, ϵ i j k is a white noise with the mean zero and variance σ 2 . We consider comparing the full top-level model M 1 versus M 0 : y i j k = μ + ϵ i j k .
Equivalently, the competing models can be expressed in the matrix-vector form as in [ 53 ], i.e.,
where y is a column vector of N observations, 1 is a column vector of N ones, τ , β , and γ are column vectors of standardized effect parameters of length a , b , and a b , respectively, X ’s are design matrices, and ϵ ∣ σ 2 ∼ N ( 0 , σ 2 I ) .
The anovaBF function of the BayesFactor package compares these linear models (including the reduced models). The ToothGrowth dataset [ 57 ] is used to study the effects of vitamin C dosage and supplement type on tooth growth in guinea pigs. The anovaBF function allows the model comparison (single-factor models, additive model, and full model) against the null model (intercept only). The following script of R code implements the multiway ANOVA.

The percentage, e.g., ± 2.73 % is the proportional Monte Carlo error estimate on the Bayes factor. The Bayes factor value of 7.94 × 10 14 suggests, according to Table 1 , very strong evidence in favor of the full model.
It is worth noting that the one-way ANOVA with two levels is consistent with the two-sample t -test, when using the default priors. For example, considering the sleep data example, one can check that:

return the same Bayes factor value (but the dataset is not meant for the independent tests).
4.3. Repeated-Measures Design
Linear mixed-effects models extend simple linear models to allow both fixed (parameters that do not vary across subjects) and random effects (parameters that are themselves random variables), particularly used when the data are dependent, multilevel, hierarchical, longitudinal, or correlated. In relation to the previous model in Section 4.2 , a linear mixed-effects model M 1 adds the standardized subject-specific random effect b k . We now consider comparing
We take the sleep dataset as an example and specify the argument whichRandom in the anovaBF function of the BayesFactor package, so that it computes the Bayes factor for such a repeated-measures design (or called a within-subjects design). The following script of R code implements the one-way repeated-measures design, where the dataset needs to be in the long format: one column is for the continuous response variable, one column is for the subject indicator, and another column is for the categorical variable indicating the levels.

This code generates a Bayes factor of about 11.468 in favor of the alternative hypothesis. The conclusion inferred from the repeated-measures designs is consistent with the earlier paired t -test result. One limitation of calling anovaBF function is that it only aims to construct the Bayes factor for a homoscedastic case.
4.4. Poisson Mixed-Effects Model
A GLM Poisson mixed-effects approach aims to model a discrete count event that was repeatedly measured at several conditions for each subject, e.g., longitudinal studies [ 58 ]. The model assumes that the response variable follows a Poisson distribution at the first level. Unlike the cases of normally distributed repeated-measures data, software used to calculate Bayes factors have not been extensively discussed and developed in the context of Bayesian Poisson models. Thus, we illustrate code for sampling the posterior using JAGS, and then the Savage–Dickey density ratio is used to approximate the Bayes factor.
When testing a nested model against an unrestricted alternative, the Bayes factor is computationally and graphically simplified as the ratio calculated by dividing the value of the posterior distribution over the parameters for the alternative model evaluated at the hypothesized value, by the prior for the same model evaluated at the same point [ 35 ] and this is the Savage–Dickey density ratio [ 34 ]. We demonstrate the use of the Savage–Dickey density ratio described in [ 59 ]. We consider fitting a Poisson mixed-effects model to a simulated dataset obtained from Appendix A . We note that the Poisson first level of this example can be changed to many other specifications from the exponential family (e.g., binomial or exponential) with only minor alterations to the code below. With data in the repeated-measures setting, the set of counts obtained from a given subject can be associated. Thus, the standard independence assumption is violated, which is a feature of repeated-measures data.
We utilize the JAGS software and rjags R package [ 60 ] to fit the model and the polspline R package to approximate the log posterior distribution [ 61 ] required to evaluate the Savage–Dickey density ratio.

The data are simulated from 48 subjects, and a count is simulated for each of two conditions on each subject. On the log-scale, conditional on the random effects, the mean in condition one is set to α 1 = 2 when the data are simulated and the corresponding value is α 2 = 2.2 for the second condition. Thus, the data are simulated under the alternative hypothesis. After fitting the model to the simulated data, the Bayes factor in favor of the alternative is B F 10 = 25.247 indicating strong evidence in favor of the alternative.
A sensitivity analysis using JAGS or Stan is convenient by passing different parameter values or changing the families of prior distributions. We specified five different prior distributions for the nuisance parameters (the intercept and the precision of the random effects) in the model statement and then examined the Bayes factors computed via the Savage–Dickey density ratio approximation. Four additional combinations of priors are shown in Table 2 . Some variation in the value of the Bayes factor is observed though the conclusion remains stable across these prior specifications.
Prior sensitivity analysis for the Poisson repeated-measures data.
| Report | beta | tau_b | ||
|---|---|---|---|---|
| 1 | dnorm(0, 0.01) | dgamma(0.01, 0.01) | 0.040 | 25.247 |
| 2 | dnorm(0, 0.1) | dgamma(0.01, 0.01) | 0.054 | 18.377 |
| 3 | dnorm(0, 0.01) | dgamma(2, 2) | 0.042 | 24.059 |
| 4 | dnorm(0, 0.1) | dgamma(2, 2) | 0.032 | 30.859 |
| 5 | dnorm(0, 0.5) | dgamma(1, 4) | 0.023 | 42.816 |
We have addressed the activity of hypothesis testing in light of empirical data. Several issues with the classical p -values and NHST approaches were reviewed to reach researchers who rarely use Bayesian testing, and NHST is still the dominant vehicle for hypothesis testing. We noted that the debate about the overuse of the p -value has been long-lasting, and there are many discussions about the misuse and misinterpretations in the literature.
Following the third principle of the ASA’s statement on p -values—i.e., research practice, business, or policy decisions should not solely rely on a p -value passing an arbitrary threshold—a Bayesian alternative method based on the Bayes factor was introduced, and the advantages and disadvantages of this approach were brought discussed. One possible caveat of the Bayes factor is its numerical computation, which has been mitigated by the advances of computational resources. We reviewed computational methods employed to approximate the marginal likelihoods, such as the bridge sampling estimator, which has an R package implementation available as an open-source solution.
Issues related to prior distributions were discussed, and we recommended a careful choice of priors via elicitation, combined with prior sensitivity analysis when using Bayes factors as a model selection tool. The Bayesian analysis and hypothesis testing are appealing, but going directly from the NHST to Bayesian hypothesis testing may require a challenging leap. Thus, we showed how, using existing software, one can practically implement statistical techniques related to the discussed Bayesian approach, and provided examples of the usage of packages intended to compute the Bayes factor, namely, in applications of the one-sample t -test, multiway ANOVA, repeated-measures designs, and Poisson mixed-effects model.
The Bayes factor is only one of many aspects of Bayesian analysis, and it serves as a bridge to Bayesian inference for researchers interested in testing. The Bayes factor can provide evidence in favor of the null hypothesis and is a relatively intuitive approach for communicating statistical evidence with a meaningful interpretation. The relationships between the Bayes factor and other aspects of the posterior distribution, for example, the overlap of Bayesian highest posterior density intervals, form a topic of interest, and we will report on this issue in another manuscript.
Appendix A. Poisson Repeated-Measures Data Simulation
The sim_Poisson R function returns a repeated-measures data frame in the long format with 2 n rows and three columns. Three columns are subject ID, count response variable, and condition levels.

Author Contributions
Conceptualization, F.S.N.; methodology, Z.W.; software, F.S.N. and Z.W.; validation, M.F.M. and A.Y.; formal analysis, Z.W.; investigation, L.R.; resources, F.S.N.; data curation, Z.W.; writing—original draft preparation, L.R., Z.W. and A.Y.; writing—review and editing, Z.W., F.S.N. and M.F.M.; visualization, Z.W.; supervision, F.S.N. and M.F.M.; project administration, F.S.N.; funding acquisition, F.S.N. and M.F.M. All authors have read and agreed to the published version of the manuscript.
This work was supported by discovery grants to Farouk S. Nathoo and Michelle F. Miranda from the Natural Sciences and Engineering Research Council: RGPIN-2020-06941. Farouk S. Nathoo holds a Tier II Canada Research Chair in Biostatistics.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Data availability statement, conflicts of interest.
The authors declare no conflict of interest.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Europe PMC requires Javascript to function effectively.
Either your web browser doesn't support Javascript or it is currently turned off. In the latter case, please turn on Javascript support in your web browser and reload this page.
- FOR INSTRUCTOR
- FOR INSTRUCTORS
9.1.8 Bayesian Hypothesis Testing
To be more specific, according to the MAP test, we choose $H_0$ if and only if
$\quad$ $H_0$: $X=1$, $\quad$ $H_1$: $X=-1$.
- in Example 9.10 , we arrived at the following decision rule: We choose $H_0$ if and only if \begin{align} y \geq c, \end{align} where \begin{align} c=\frac{\sigma^2}{2} \ln \left(\frac{1-p}{p}\right). \end{align} Since $Y|H_0 \; \sim \; N(1, \sigma^2)$, \begin{align} P( \textrm{choose }H_1 | H_0)&=P(Y \lt c|H_0)\\ &=\Phi\left(\frac{c-1}{\sigma} \right)\\ &=\Phi\left(\frac{\sigma}{2} \ln \left(\frac{1-p}{p}\right)-\frac{1}{\sigma}\right). \end{align} Since $Y|H_1 \; \sim \; N(-1, \sigma^2)$, \begin{align} P( \textrm{choose }H_0 | H_1)&=P(Y \geq c|H_1)\\ &=1-\Phi\left(\frac{c+1}{\sigma} \right)\\ &=1-\Phi\left(\frac{\sigma}{2} \ln \left(\frac{1-p}{p}\right)+\frac{1}{\sigma}\right). \end{align} Figure 9.4 shows the two error probabilities for this example. Therefore, the average error probability is given by \begin{align} P_e &=P( \textrm{choose }H_1 | H_0) P(H_0)+ P( \textrm{choose }H_0 | H_1) P(H_1)\\ &=p \cdot \Phi\left(\frac{\sigma}{2} \ln \left(\frac{1-p}{p}\right)-\frac{1}{\sigma}\right)+(1-p) \cdot \left[ 1-\Phi\left(\frac{\sigma}{2} \ln \left(\frac{1-p}{p}\right)+\frac{1}{\sigma}\right)\right]. \end{align}
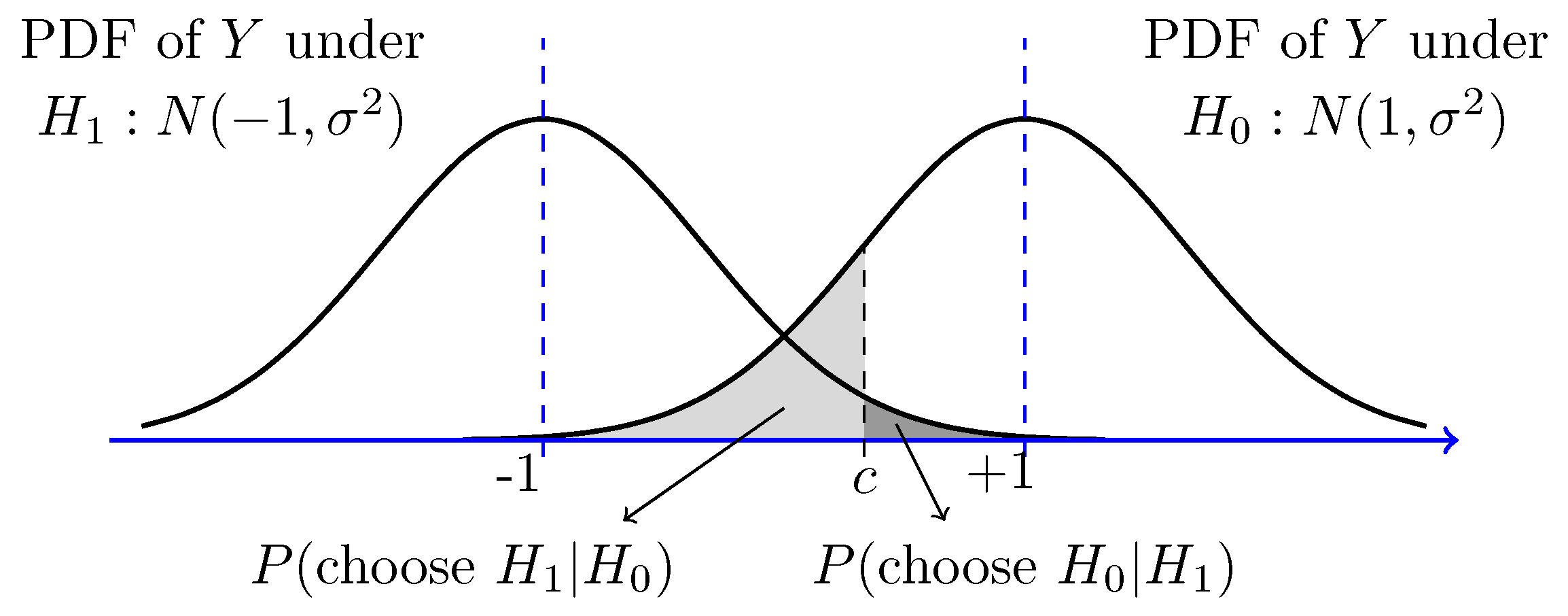
Minimum Cost Hypothesis Test:
$\quad$ $H_0$: There is no fire, $\quad$ $H_1$: There is a fire.
$\quad$ $C_{10}$: The cost of choosing $H_1$, given that $H_0$ is true. $\quad$ $C_{01}$: The cost of choosing $H_0$, given that $H_1$ is true.
$\quad$ $H_0$: No intruder is present. $\quad$ $H_1$: There is an intruder.
- First note that \begin{align} P(H_0|y)=1-P(H_1|y)=0.95 \end{align} The posterior risk of accepting $H_1$ is \begin{align} P(H_0|y) C_{10} =0.95 C_{10}. \end{align} We have $C_{01}=10 C_{10}$, so the posterior risk of accepting $H_0$ is \begin{align} P(H_1|y) C_{01} &=(0.05) (10 C_{10})\\ &=0.5 C_{10}. \end{align} Since $P(H_0|y) C_{10} \geq P(H_1|y) C_{01}$, we accept $H_0$, so no alarm message needs to be sent.
The print version of the book is available on . |
|
- Search Menu
- Sign in through your institution
- Supplements
- Advance articles
- Editor's Choice
- Special Issues
- Author Guidelines
- Submission Site
- Why Publish With Us?
- Open Access
- About Nicotine & Tobacco Research
- About Society for Nicotine & Tobacco Research
- Editorial Board
- Advertising and Corporate Services
- Journals Career Network
- Self-Archiving Policy
- Dispatch Dates
- Journals on Oxford Academic
- Books on Oxford Academic

Article Contents
Introduction, conceptualizing hypothesis testing via bayes factors, empirical example 1: is a coin fair or tail-biased, empirical example 2: do health warnings for e-cigarettes increase worry about health, conclusions, declaration of interests.
- < Previous
Bayesian Inference: An Introduction to Hypothesis Testing Using Bayes Factors
- Article contents
- Figures & tables
- Supplementary Data
Sabeeh A Baig, Bayesian Inference: An Introduction to Hypothesis Testing Using Bayes Factors, Nicotine & Tobacco Research , Volume 22, Issue 7, July 2020, Pages 1244–1246, https://doi.org/10.1093/ntr/ntz207
- Permissions Icon Permissions
Monumental advances in computing power in recent decades have contributed to the rising popularity of Bayesian methods among applied researchers. This series of commentaries seeks to raise awareness among nicotine and tobacco researchers of Bayesian methods for analyzing experimental data. The current commentary introduces statistical inference via Bayes factors and demonstrates how they can be used to present evidence in favor of both alternative and null hypotheses.
Bayesian inference is a fully probabilistic framework for drawing scientific conclusions that resembles how we naturally think about the world. Often, we hold an a priori position on a given issue. On a daily basis, we are confronted with facts about that issue. We regularly update our position in light of those facts. Bayesian inference follows this exact updating process. Formally stated, given a research question, at least one unknown parameter of interest, and some relevant data, Bayesian inference follows three basic steps. The process begins by specifying a prior probability distribution on the unknown parameter that often reflects accumulated knowledge about the research question. Next, the observed data, summarized using a likelihood function, are conditioned on the prior distribution. Finally, the resulting posterior distribution represents an updated state of knowledge about the unknown parameter and, by extension, the research question. Simulating data many times from the posterior distribution will ideally yield representative samples of the unknown parameter that we can interpret to answer the research question.
In an experimental context, we are often interested in evaluating two competing positions or hypotheses in light of data and making a determination about which to accept. In the context of Bayesian inference, hypothesis testing can be framed as a special case of model comparison where a model refers to a likelihood function and a prior distribution. Given two competing hypotheses and some relevant data, Bayesian hypothesis testing begins by specifying separate prior distributions to quantitatively describe each hypothesis. The combination of the likelihood function for the observed data with each of the prior distributions yields hypothesis-specific models. For each of the hypothesis-specific models, averaging (ie, integrating) the likelihood with respect to the prior distribution across the entire parameter space yields the probability of the data under the model and, therefore, the corresponding hypothesis. This quantity is more commonly referred to as the marginal likelihood and represents the average fit of the model to the data. The ratio of the marginal likelihoods for both hypothesis-specific models is known as the Bayes factor.
The Bayes factor is a central quantity of interest in Bayesian hypothesis testing. A Bayes factor has a range of near 0 to infinity and quantifies the extent to which data support one hypothesis over another. Bayes factors can be interpreted continuously so that a Bayes factor of 30 indicates that there is 30 times more support in the data for a given hypothesis than the alternative. They can also be interpreted discretely so that a Bayes factor of 3 or higher supports accepting a given hypothesis, 0.33 or lower supports accepting its alternative, and values in between are inconclusive. 1 , 2 Intuitively, the Bayes factor is the ratio of the odds of observing two competing hypotheses after examining relevant data compared to the odds of observing those hypotheses before examining the data. Therefore, the Bayes factor represents how we should update our knowledge about the hypotheses after examining data. We present two empirical examples with simulated data to demonstrate the computation and use of Bayes factors to test hypotheses.
Deciding whether a coin is fair or tail-biased is a simple, but useful example to illustrate hypothesis testing via Bayes factors. Let the null hypothesis be that the coin is fair, and let the alternative hypothesis be that the coin is tail-biased. We further intuit that coins, fair or not, can exhibit a considerable degree of variation in their head-tail biases depending on quality control issues during the minting process. Therefore, we use a Beta(5, 5) prior distribution to describe the null hypothesis. This distribution places the bulk of the probability density at or around 0.5 (ie, equal probability of heads or tails). Similarly, we use a Beta(3.8, 6.2) prior distribution to describe the alternative hypothesis. This skewed distribution places the bulk of the density at or around 0.35 (ie, lower probability of heads) and places less density on values greater than 0.4. The Beta prior is appropriate to describe hypotheses about a coin (and other binary variables) because it is continuously defined on the interval between 0 and 1 that the bias of a coin is also defined on; has hyperparameters that can be interpreted as the number of heads and tails; and provides flexibility in describing hypotheses because it does not have to be symmetric.
To test these hypotheses, we conduct a simple experiment by flipping the coin 20 times, recording 5 heads and 15 tails. We summarize this data using a Bernoulli(5, 15) likelihood function. After computing the marginal likelihoods of the models for both hypotheses, we find that the Bayes factor comparing the alternative hypothesis to the null is 2.65. This indicates that the data supports the alternative hypothesis that the coin is tail-biased over the null hypothesis that it is fair only by a factor of 2 or so. We further note that the Bayes factor falls into the range of inconclusive values. Therefore, we conclude that we need more experimental data to determine whether the coin is fair or tail-biased with greater certainty.
A more pertinent illustrative example of hypothesis testing via Bayes factors is deciding whether health warnings for e-cigarettes increase worry about one’s health. Let the null hypothesis be that health warnings have exactly no effect on worry. Let the first alternative hypothesis be one-sided that health warnings increase worry, and let the second alternative hypothesis also be one-sided that health warnings decrease worry. Bayes factors with the Jeffreys-Zellner-Siow (JZS) default prior can be used to evaluate these hypotheses. 3 In comparison to other priors, default priors have mathematical properties that simplify the computation of Bayes factors. The JZS default prior describes hypotheses in terms of possible effect sizes (ie, Cohen’s d ). As such, under the null hypothesis that health warnings have exactly no effect on worry, the prior distribution places the entire density on an effect size of 0 ( Figure 1 ). Given that effect sizes in behavioral research in tobacco control are usually small, 4–6 the prior distributions for the alternative hypotheses use a scale parameter of 1/2 to distribute the density mostly over small positive or negative effect sizes.

Prior distributions quantitatively describing competing hypotheses about the effect of e-cigarette health warnings on worry about one’s own health due to tobacco product use.
To test these hypotheses, we conduct a simple online experiment with 200 adults who vape every day or some days. The experiment randomizes participants to receive a stimulus depicting 1 of 5 e-cigarette devices (eg, vape pen) with or without a corresponding health warning. After viewing the stimulus for 10 seconds, participants complete a survey that includes an item on worry, “How worried are you about your health because of your e-cigarette use?”, 7 with a response scale of 1 (“not at all”) to 5 (“extremely”). Participants who receive a health warning elicit mean worry of 2.38 ( SD = 0.87), and those who do not elicit mean worry of 2.33 ( SD = 0.84). The Bayes factors comparing the first and second alternative hypotheses to the null hypothesis are 0.16 and 0.30, respectively. These Bayes factors indicate that there is more support in the data for the null hypothesis than the alternative hypotheses. Taking the reciprocal of these Bayes factors indicates that there is approximately 3 to 6 times more support in the data for the null hypothesis that health warnings have no effect than either alternative. Therefore, we conclude that health warnings for e-cigarettes do not appear to affect worry based on the experimental data.
The hallmark of Bayesian model comparison (and other Bayesian approaches) is the incorporation of uncertainty at all stages of inference, particularly through the use of properly specified prior distributions. As a result, Bayesian model comparison has three practical advantages over conventional methods. First, Bayesian model comparison is not limited to tests of point null hypotheses. 8 , 9 In fact, the first empirical example essentially conceptualized the possibility of the coin being fair as an interval null hypothesis by permitting some unfair head-coin biases. Indeed, a great deal has already been written on how the use of point null hypotheses can lead to overstatements about the evidence for alternative hypotheses. 10 Second, Bayesian model comparison is flexible enough to permit tests of any meaningful hypotheses. 11 As a result, the second empirical example demonstrated tests of two one-sided hypotheses against the same null hypothesis. Third, Bayesian model comparison uses the marginal likelihood, which is a measure of the average fit of a model across the parameter space. 12 Doing so leads to more accurate characterizations of the evidence for competing hypotheses because they account for uncertainty in parameter values even after observing the data instead of only focusing on the most likely values of those parameters.
Bayes factors specifically have three advantages over other inferential statistics. First, Bayes factors can provide direct evidence for the common null hypothesis of no difference. 13 Second, they can reveal when experimental data is insensitive to the null and alternative hypotheses, clearly suggesting that the researcher should withhold judgment. 13 Third, they can be interpreted continuously and thus provide an indication of the strength of the evidence for the null or alternative hypothesis. While Bayesian model comparison via Bayes factors leads to robust tests of competing hypotheses, this advantage is only realized when all hypotheses are quantitatively described using carefully chosen priors that are calibrated in light of accumulated knowledge. Furthermore, two analysts may choose different priors to describe the same hypothesis. This subjectivity in the choice of prior has promoted the development of a large class of Bayes factors for common analyses (eg, difference of means as illustrated in the second empirical example) that use default priors. 14–16 Thus, the analyst only needs to choose values for important parameters, as in the second empirical example, without having to select the functional form of the prior (eg, a Beta prior) as in the first empirical example. Published Bayesian analyses will often list priors and justify why they were chosen for full transparency (see Baig et al. 17 for one succinct example). The next commentary will focus on informative hypotheses, prior specification when computing corresponding Bayes factors, and some Bayesian solutions for multiple testing. For the curious reader, the JASP package provides access to Bayes factors that use default priors for common analyses through a point-and-click interface similar to SPSS. 18
This work was supported by the Office of The Director, National Institutes of Health (award number DP5OD023064).
None declared.
Rouder JN , Morey RD , Verhagen J , Swagman AR , Wagenmakers EJ . Bayesian analysis of factorial designs . Psychol Methods. 2017 ; 22 ( 2 ): 304 – 321 .
Google Scholar
Jeon M , De Boeck P . Decision qualities of Bayes factor and p value-based hypothesis testing . Psychol Methods. 2017 ; 22 ( 2 ): 340 – 360 .
Hoijtink H , van Kooten P , Hulsker K . Why bayesian psychologists should change the way they use the Bayes factor . Multivariate Behav Res . 2016 ; 51 ( 1 ): 2 – 10 . doi:10.1080/00273171.2014.969364
Baig SA , Byron MJ , Boynton MH , Brewer NT , Ribisl KM . Communicating about cigarette smoke constituents: an experimental comparison of two messaging strategies . J Behav Med. 2017 ; 40 ( 2 ): 352 – 359 .
Brewer NT , Morgan JC , Baig SA , et al. Public understanding of cigarette smoke constituents: three US surveys . Tob Control. 2016 ; 26 ( 5 ): 592 – 599 .
Morgan JC , Byron MJ , Baig SA , Stepanov I , Brewer NT . How people think about the chemicals in cigarette smoke: a systematic review . J Behav Med . 2017 ; 40 ( 4 ): 553 – 564 . doi:10.1007/s10865-017-9823-5
Mendel JR , Hall MG , Baig SA , Jeong M , Brewer NT . Placing health warnings on e-cigarettes: a standardized protocol . Int J Environ Res Public Health . 2018 ; 15 ( 8 ): 1578 . doi:10.3390/ijerph15081578
Morey RD , Rouder JN . Bayes factor approaches for testing interval null hypotheses . Psychol Methods. 2011 ; 16 ( 4 ): 406 – 419 .
West R . Using Bayesian analysis for hypothesis testing in addiction science . Addiction . 2016 ; 111 ( 1 ): 3 – 4 . doi:10.1111/add.13053
Berger JO , Sellke T . Testing a point null hypothesis: the irreconcilability of p-values and evidence . J Am Stat Assoc . 1987 ; 82 ( 397 ): 112 – 122 . doi:10.1080/01621459.1987.10478397
Etz A , Haaf JM , Rouder JN , Vandekerckhove J . Bayesian inference and testing any hypothesis you can specify . Adv Methods Pract Psychol Sci . 2018 ; 1 ( 2 ): 281 – 295 . doi:10.1177/2515245918773087
Etz A . Introduction to the concept of likelihood and its applications . Adv Methods Pract Psychol Sci . 2018 ; 1 ( 1 ): 60 – 69 . doi:10.1177/2515245917744314
Dienes Z , Coulton S , Heather N . Using Bayes factors to evaluate evidence for no effect: examples from the SIPS project . Addiction. 2018 ; 113 ( 2 ): 240 – 246 .
Nuijten MB , Wetzels R , Matzke D , Dolan CV , Wagenmakers E-J . A default Bayesian hypothesis test for mediation . Behav Res Methods . 2014 ; 47 ( 1 ): 85 – 97 . doi:10.3758/s13428-014-0470-2
Ly A , Verhagen J , Wagenmakers E-J . Harold Jeffreys’s default Bayes factor hypothesis tests: explanation, extension, and application in psychology . J Math Psychol . 2016 ; 72 : 19 – 32 . doi:10.1016/j.jmp.2015.06.004
Rouder JN , Speckman PL , Sun D , Morey RD , Iverson G . Bayesian t tests for accepting and rejecting the null hypothesis . Psychon Bull Rev. 2009 ; 16 ( 2 ): 225 – 237 .
Baig SA , Byron MJ , Lazard AJ , Brewer NT . “Organic,” “natural,” and “additive-free” cigarettes: comparing the effects of advertising claims and disclaimers on perceptions of harm . Nicotine Tob Res . 2019 ; 21 ( 7 ): 933 – 939 .
Wagenmakers E-J , Love J , Marsman M , et al. Bayesian inference for psychology. Part ii: example applications with JASP . Psychon Bull Rev . 2018 ; 25 ( 1 ): 58 – 76 .
- electronic cigarettes
| Month: | Total Views: |
|---|---|
| November 2019 | 111 |
| December 2019 | 53 |
| January 2020 | 55 |
| February 2020 | 97 |
| March 2020 | 84 |
| April 2020 | 106 |
| May 2020 | 88 |
| June 2020 | 196 |
| July 2020 | 200 |
| August 2020 | 242 |
| September 2020 | 362 |
| October 2020 | 568 |
| November 2020 | 609 |
| December 2020 | 578 |
| January 2021 | 593 |
| February 2021 | 625 |
| March 2021 | 682 |
| April 2021 | 619 |
| May 2021 | 663 |
| June 2021 | 536 |
| July 2021 | 432 |
| August 2021 | 428 |
| September 2021 | 495 |
| October 2021 | 598 |
| November 2021 | 467 |
| December 2021 | 396 |
| January 2022 | 448 |
| February 2022 | 467 |
| March 2022 | 517 |
| April 2022 | 569 |
| May 2022 | 617 |
| June 2022 | 462 |
| July 2022 | 429 |
| August 2022 | 380 |
| September 2022 | 381 |
| October 2022 | 485 |
| November 2022 | 505 |
| December 2022 | 373 |
| January 2023 | 453 |
| February 2023 | 594 |
| March 2023 | 717 |
| April 2023 | 592 |
| May 2023 | 596 |
| June 2023 | 462 |
| July 2023 | 359 |
| August 2023 | 403 |
| September 2023 | 430 |
| October 2023 | 657 |
| November 2023 | 562 |
| December 2023 | 390 |
| January 2024 | 468 |
| February 2024 | 544 |
| March 2024 | 610 |
| April 2024 | 696 |
| May 2024 | 485 |
| June 2024 | 301 |
Email alerts
Citing articles via.
- About Nicotine & Tobacco Research
- Recommend to your Library
Affiliations
- Online ISSN 1469-994X
- Copyright © 2024 Society for Research on Nicotine and Tobacco
- About Oxford Academic
- Publish journals with us
- University press partners
- What we publish
- New features
- Open access
- Institutional account management
- Rights and permissions
- Get help with access
- Accessibility
- Advertising
- Media enquiries
- Oxford University Press
- Oxford Languages
- University of Oxford
Oxford University Press is a department of the University of Oxford. It furthers the University's objective of excellence in research, scholarship, and education by publishing worldwide
- Copyright © 2024 Oxford University Press
- Cookie settings
- Cookie policy
- Privacy policy
- Legal notice
This Feature Is Available To Subscribers Only
Sign In or Create an Account
This PDF is available to Subscribers Only
For full access to this pdf, sign in to an existing account, or purchase an annual subscription.
How to use and report Bayesian hypothesis tests
Chat with Paper: Save time, read 10X faster with AI
Content maybe subject to copyright Report

Bayesian Analysis Reporting Guidelines.
Does high variability training improve the learning of non-native phoneme contrasts over low variability training a replication, supplemental materials for preprint: optional stopping and the interpretation of the bayes factor, diverging implicit measurement of sense of agency using interval estimation and libet clock, unconscious knowledge of rewards guides instrumental behaviors via conscious judgments., development and validation of brief measures of positive and negative affect: the panas scales., estimating the reproducibility of psychological science, conjectures and refutations: the growth of scientific knowledge, the design of experiments, bayesian t tests for accepting and rejecting the null hypothesis, related papers (5), bayesian hypothesis testing for proportions, why bayesian “evidence for h1” in one condition and bayesian “evidence for h0” in another condition does not mean good-enough bayesian evidence for a difference between the conditions:, the strength of statistical evidence for composite hypotheses: inference to the best explanation, properties of hypothesis testing techniques and (bayesian) model selection for exploration-based and theory-based (order-restricted) hypotheses., posterior odds ratios for regression hypotheses: general considerations and some specific results, frequently asked questions (1), q1. what are the contributions in this paper.
This article provides guidance on interpreting and reporting Bayesian hypothesis tests, in order to aid their understanding. The paper will provide guidance in specifying effect sizes of interest ( which also will be of relevance to those using frequentist statistics ).
- DOI: 10.31234/osf.io/bua5n
- Corpus ID: 242437349
How to use and report Bayesian hypothesis tests
- Published 3 April 2020
One Citation
Strategies that reduce stroop interference, related papers.
Showing 1 through 3 of 0 Related Papers
An R companion to Statistics: data analysis and modelling
Chapter 13 bayesian hypothesis testing with bayes factors.
In this chapter, we will discuss how to compute Bayes Factors for a variety of General Linear Models using the BayesFactor package ( Morey and Rouder 2023 ) . The package implements the “default” priors discussed in the SDAM book.
13.1 The BayesFactor package
The BayesFactor package implements Bayesian model comparisons for General Linear Models (as well as some other models for e.g. contingency tables and proportions) using JZS-priors for the parameters, or fixing those parameters to 0. Because Bayes Factors are transitive , in the sense that a ratio of Bayes Factors is itself another Bayes factor: \[\begin{align} \text{BF}_{1,2} &= \frac{p(Y_1,\ldots,Y_n|\text{MODEL 1})}{p(Y_1,\ldots,Y_n|\text{MODEL 2})} \\ &= \frac{p(Y_1,\ldots,Y_n|\text{MODEL 1})/p(Y_1,\ldots,Y_n|\text{MODEL 0})} {p(Y_1,\ldots,Y_n|\text{MODEL 2})/p(Y_1,\ldots,Y_n|\text{MODEL 0})} \\ &= \frac{\text{BF}_{1,0}}{\text{BF}_{2,0}} , \end{align}\] you can compute many other Bayes Factors which might not be immediately provided by the package, by simply dividing the Bayes factors that the package does provide. This makes the procedure of model comparison very flexible.
If you haven’t installed the BayesFactor package yet, you need to do so first. Then you can load it as usual by:
13.1.1 A Bayesian one-sample t-test
A Bayesian alternative to a \(t\) -test is provided via the ttestBF function. Similar to the base R t.test function of the stats package, this function allows computation of a Bayes factor for a one-sample t-test or a two-sample t-tests (as well as a paired t-test, which we haven’t covered in the course). Let’s re-analyse the data we considered before, concerning participants’ judgements of the height of Mount Everest. The one-sample t-test we computed before, comparing the judgements to an assumed mean of \(\mu = 8848\) , was:
The syntax for the Bayesian alternative is very similar, namely:
This code provides a test of the following models:
\[\begin{align} H_0\!&: \mu = 8848 \\ H_1\!&: \frac{\mu - 8848}{\sigma_\epsilon} \sim \textbf{Cauchy}(r) \end{align}\]
After computing the Bayes factor and storing it in an object bf_anchor , we just see the print-out of the result by typing in the name of the object:
This output is quite sparse, which is by no means a bad thing. It shows a few important things. Under Alt. (which stands for the alternative hypothesis), we first see the scaling factor \(r\) used for the JZS prior distribution on the effect size. We then see the value of the Bayes Factor, which is “extreme” (>100), showing that the data increases the posterior odds ratio for the alternative model over the null model by a factor of 46,902,934,288. Quite clearly, the average judgements differed from the true height of Mount Everest! After the computed value of the Bayes factor, you will find a proportional error for the estimate of the Bayes factor. In general, the marginal likelihoods that constitute the numerator (“top model”) and denominator (“bottom model”) of the Bayes factor cannot be computed exactly, and have to be approximated by numerical integration routines or simulation. This results in some (hopefully small) error in computation, and the error estimate indicates the extend to which the true Bayes factor might differ from the computed one. In this case, the error is (proportionally) very small, and hence we can be assured that our conclusion is unlikely to be affected by error in the approximation.
As we didn’t set the scaling factor explicitly, the default value is used, which is the “medium” scale \(r = \frac{\sqrt{2}}{2} = 0.707\) . Note that this is actually different from the default value of \(r=1\) proposed in Rouder et al. ( 2009 ) , which first introduced this version of the Bayesian \(t\) -test to a psychological audience, and the one used to illustrate the method in the SDAM book. Whilst reducing the default value to \(r=0.707\) is probably reasonable given the effect sizes generally encountered in psychological studies, a change in the default prior highlights the subjective nature of the prior distribution in the Bayesian model comparison procedure. You should also realise that different analyses, such as t-tests, ANOVA, and regression models, use different default values for the scaling factor. As shown in the SDAM book, the value of the Bayes factor depends on the choice for the scaling factor. Although the default value may be deemed reasonable, the choice should really be based on a consideration of the magnitude of the effect sizes you (yes, you!) expect in a particular study. This is not always easy, but you should pick one (the default value, for instance, if you can’t think of a better one) before conducting the analysis. If you feel that makes the test too subjective, you may may want to check the robustness of the result for different choices of the scaling factor. You can do this by computing the Bayes factor for a range of choices of the scaling factor, and then inspecting whether the strength of the evidence is in line with your choice for a reasonable range of values around your choice. The code below provides an example of this:

Given the scale of the \(y\) -axis (e.g., the first tick mark is at 1e+10 = 10,000,000,000), there is overwhelming evidence against the null-hypothesis for most choices of the scaling factor. Hence, the results seem rather robust to the exact choice of prior.
13.1.2 A Bayesian two-sample t-test
To compare the means of two groups, we can revisit the Tetris study, where we considered whether the number of memory intrusions is reduced after playing Tetris in combination with memory reactivation, compared to just memory reactivation by itself. The ttestBF function allows us to provide the data for one group as the x argument, and the data for the other group as the y argument, so we can perform our model comparison, by subsetting the dependent variable appropriately, as follows:
Which shows strong evidence for the alternative hypothesis over the null hypothesis that the means are identical (i.e. that the difference between the means is zero, \(\mu_1 - \mu_2 = 0\) ), as the alternative model is 2.82 times more likely than the null model, which sets the difference between the means to exactly \(\mu_1 - \mu_2 = 0\) , rather than allowing different values of this difference through the prior distribution.
A two-sample t-test should really be identical to a two-group ANOVA model, as both concern the same General Linear Model (a model with a single contrast-coding predictor, with e.q. values of \(-\tfrac{1}{2}\) and \(\tfrac{1}{2}\) ). Before fully discussing the way to perform an ANOVA-type analysis with the BayesFactor package, let’s just double-check this is indeed the case:
The results are indeed identical. Note that this is because both the ttestBF and anovaBF function use the same prior distribution for the effect.
13.1.3 A Bayesian ANOVA
More general ANOVA-type models can be tested though the anovaBF function. This function takes the following important arguments:
- formula : a formula like in the lm function, specifying which factors to include as well as their interactions (by e.g. using an * operator to specify you want to include the main effects as well as their interactions. Note that unlike in the lm function, all terms must be factors .
- data : a data.frame containing data for all factors in the formula.
- whichRandom : a character vector specifying which factors are random. Random factors can be used to obtain a model similar to a repeated-measures ANOVA, or a (restricted) set of linear-mixed effects models (with only factors for the fixed effects).
- whichModels : a character vector specifying which models to compare. The allowed values are "all" , "withmain" (the default), "top" , and "bottom" . Setting whichModels to "all" will test all models that can be created by including or not including a main effect or interaction. "top" will test all models that can be created by removing or leaving in a main effect or interaction term from the full model. "bottom" creates models by adding single factors or interactions to the null model. "withmain" will test all models, with the constraint that if an interaction is included, the corresponding main effects are also included. Setting the argument to top produces model comparisons similar to the Type 3 procedure, comparing the full model to a restricted model with each effect removed. Setting the argument to withMain produces model comparisons similar to the Type 2 procedure, with model comparisons that respect the “principle of marginality”, such that tests of the main effects do not consider higher-order interactions, whilst a test of any interaction includes the main effects that constitute the elements in the interactions.
- rscaleFixed : prior scale for fixed effects. The value can be given numerically, or as one of three strings: "medium" ( \(r = \tfrac{1}{2}\) ), "wide" : \(r = \tfrac{\sqrt{2}}{2}\) , or "ultrawide" ( \(r=1\) ). The default is “ medium" .
- rscaleRandom : prior scale for random effects. Accepts the same strings as rscaleFixed , and in addition "nuisance" ( \(r = 1\) ). The default is "nuisance" .
- rscaleEffects : a named vector with prior scales for individual factors.
The anovaBF function will (as far as I can gather) always use contr.sum() contrasts for the factors . So setting your own contrasts will have no effect on the results. The exact contrast should not really matter for omnibus tests, and sum-to-zero are a reasonable choice in general ( contr.sum implements what we called effect-coding before). 3 While the anovaBF function always uses the JZS prior for any effects, it allows you to specify exactly which scaling factor to use for every effect, if so desired. One perhaps confusing thing is that effect-sizes for ANOVA designs (as far as I can gather) are based on standardized treatment-effects, whilst those for the t-test designs are based on Cohens- \(d\) effect sizes. Hence, the values of the scaling factor \(r\) for “medium”, “wide”, and “ultrawide” are different for the Bayesian \(t\) -test and ANOVA models (whilst they provide the same results for models with two conditions).
Let’s see what happens when we use a Bayesian ANOVA-type analysis for the data on experimenter beliefs in social priming. First, let’s load the data, and turn the variables reflecting the experimental manipulations into factors:
We can now use the anovaBF function to compute the Bayes factors:
A main thing to note here is that the comparisons of different versions of MODEL G are against the same MODEL R, which is an intercept-only model. We can see that all models which include experimenterBelief receive strong evidence against the intercept-only model, apart from the model which only includes primeCond , which has less evidence than the intercept-only model. Although this indicates that the primeCond effect might be ignorable, the comparisons are different from comparing reduced models to the general MODEL G with all effects included. We can obtain these Type 3 comparisons by setting the whichModels argument to `top``:
It is very important to realise that the output now concerns the comparison of the reduced model (in the numerator, i.e. the “top model”) against the full model (in the denominator, i.e. the “bottom model”), as is stated in the Against denimonator part of the output. So these are \(\text{BF}_{0,1}\) values, rather than \(\text{BF}_{1,0}\) values. That means that low values of the Bayes factor now indicate evidence for the alternative hypothesis that an effect is different from 0. As we find a very low \(\text{BF}_{0,1}\) value for the experimenterBelief effect, this thus shows strong evidence that this effect is different than 0. The \(\text{BF}_{0,1}\) values for the other effects are larger than 1, which indicate more support for the null hypothesis than for the alternative hypothesis.
We can change the output from a \(\text{BF}_{0,1}\) value to a \(\text{BF}_{1,0}\) value by simply inverting the Bayes factors, as follows:
As we noted before, we again see strong evidence for the effect of experimenterBelief when we remove it from the full model, but not for the other effects.
The transitivity of the Bayes factor means that we can also obtain some of these results through a ratio of the Bayes factors obtained earlier. For instance, a Type 3 test of the effect of experimenterBelief:primeCond interaction can be obtained by comparing a model with all effects included to a model without this interaction. In the analysis stored in bf_expB , we compared a number of the possible models to an intercept-only model. By comparing the Bayes factors of the model which excludes the interaction to a model which includes it, we can obtain the same Bayes factor of that interaction as follows. In the output of bf_expB , the fourth element compared the full model to the intercept-only model, whilst in the third element, a model with only the main effects of experimenterBelief and primeCond are compared to an intercept-only model. The Type 3 test of the interaction can then be obtained through the ratio of these two Bayes factors:
which indicates evidence for the null hypothesis that there is no moderation of the effect of experimenterbelief by primeCond , as the Bayes factor is well below 1. We cannot replicate all Type 3 analyses with the results obtained earlier, unless we ask the function to compare every possible model against the intercept-only model, by specifying whichModels = "all" :
For instance, we can now obtain a Type 3 test for experimenterBelief by comparing the full model (the 7th element in the output) to a model which just excludes this effect (i.e. the 6th element):
which reproduces mostly the result we obtained by setting whichModel = "top" before.
13.1.4 Bayesian regression and ANCOVA
Apart from different default values of the scaling factor \(r\) in the scaled-Cauchy distribution, the BayesFactor package works in the same way for models which include metric predictors. In a multiple regression model with only metric predictors, we can use the convenience function regressionBF . If you want to mix metric and categorical predictors, as in an ANCOVA model, you will have to use the generalTestBF function. All functions discussed so far are really just convenience interfaces to the generalTestBF , which implements Bayes factors for the General Linear Model. These convenience functions are used to determine an appropriate scaling factor for the different terms in the model, but not much else of concern, so you can replicate all the previous analyses through the generalTestBF function, if you’d like.
13.1.5 Bayesian repeated-measures ANOVA
An analysis similar to a repeated-measures ANOVA can also be obtained. Just like the afex package, the BayesFactor package requires data in the long format. Let’s first prepare the data of the Cheerleader-effect experiment:
The way the BayesFactor package deals with repeated-measures designs is a little different from how we treated repeated-measures ANOVA. Rather than computing within-subjects composite variables, the package effectively deals with individual differences by adding random intercepts (like in a linear mixed-effects model). To do this, we add Participant as an additive effect, and then classify it as a random effect through the whichRandom argument. To obtain Type-3 comparisons, we again set whichModels to top :
In this case, the proportional errors of the results may be deemed to high. We can get more precise results by obtaining more samples (for these complex models, the estimation of the Bayes factor is done with a sampling-based approximation). We can do this, without the need to respecify the model, with the recompute function, where we can increase the number of sampling iterations from the default (10,000 iterations) to something higher:
This provides somewhat better results, although it would be better to increase the number of iterations even more.
As before, the Bayes Factors are for the reduced model compared to the full model and we can get more easily interpretable results by computing the inverse value
We can see that we obtain “extreme” evidence for the main effect of Item. For the other effects, the evidence is more in favour of the null-hypothesis.
13.1.6 Parameter estimates
By default, the Bayes Factor objects just provide the values of the Bayes Factor. We don’t get estimates of the parameters.
To get (approximate) posterior distributions for the parameters, we can first estimate the general MODEL G with the lmBF function. This function is meant to compute a specific General Linear Model (rather than a set of such models). For example, for the Social Priming example, we can estimate the ANOVA model with lmBF as:
We can then use this estimated model to obtain samples from the posterior distribution over the model parameters. This is done with the posterior function of the Bayesfactor package. We can determine the number of samples through the iterations argument. This should generally be a high number, to get more reliable estimates:
The post_samples object can be effectively treated as a matrix, with columns corresponding to the different parameters, and in the rows the samples. So we can obtain posterior means as the column-wise averages:
Here, mu corresponds to the “grand mean” (i.e. the average of averages), which is is the intercept in a GLM with sum-to-zero contrasts. The next mean corresponds to the posterior mean of the treatment effect of the high-power prime condition ( primeCond-HPP ). I.e., this is the marginal mean of the high-power prime conditions, compared to the grand mean. The second effect is the posterior mean of the treatment effect of the low-power prime condition ( primeCond-LPP ). As there are only two power-prime conditions, this is exactly the negative value of the posterior mean of the high-power prime treatment effect (the grand mean is exactly halfway between these two treatment effects). We get similar treatment effects for the main effect of experimenter belief, and the interaction between power prime and experimenter belief. The posterior mean labelled sig2 is an estimate of the error variance. The columns after this are values related to the specification of the prior, which we will ignore for now.
We can do more than compute means for these samples from the posterior distribution. For instance, we can plot the (approximate) posterior distributions as well. For example, we can plot the posterior distribution of the high-power prime treatment effect as:

13.1.7 Highest-density interval
A convenient way to obtain highest-density intervals, is by using the hdi function from the HDInterval package ( R-HDInterval? ) . This function is defined for a variety of objects, including those returned by the BayesFactor::posterior() function. The function has, in addition to the object, one more argument called credMass , which specifies the width of the credible interval ( credMass = .95 is the default). For example, the 95% HDI interval for the two parameters that we plotted above are obtained as follows:
The output shows the lower and upper bound for each HDI. We see that the 95% HDI for power prime effect includes 0, whilst the 95% HDI for the experimenter belief effect does not. Again, this corresponds to what we observed earlier, that there is strong evidence for the experimenter belief effect, but not for the power prime effect.
13.2 Bayes Factors for brms models
The BayesFactor package computes Bayes Factors for a number of standard analyses, using the default priors set in the package. We may want to compute Bayes Factors to test hypotheses for more complex models. In general, we can compare any models by first computing the marginal likelihood for each model, and then computing the Bayes Factor as the ratio of these marginal likelihoods. Computing marginal likelihoods is not always straightforward, but a general procedure that often works reasonably well is called “bridge sampling” ( Quentin F. Gronau et al. 2017 ) , and has been implemented in the bridgesampling ( Quentin F. Gronau and Singmann 2021 ) package. Before discussing how to use this, we will first discuss a simpler way to compute Bayes Factors for particular comparisons within the context of a brms model.
For the following examples, we will start with the multiple regression model for the trump2016 data that we also estimated in the previous chapter, but now setting the prior distributions to more informative ones, as is advisable when computing Bayes Factors:
The results of this model are
13.2.1 Testing simple point and directional hypotheses for parameters of brms models
The brms::hypothesis() function can be used to test hypotheses about single parameters of brms models. This requires to set the argument sample_prior=TRUE in the brms::brm() function. The brms::hypothesis() function will not work properly without this. The brms::hypothesis() function has the following important arguments:
- x : a model of class brmsfit as fitted by brms::brm() . It can also be a data.frame with posterior draws (in rows) of parameters (in columns).
- hypothesis : a character vector describing hypotheses to be tested.
- class : a string specifying the class of parameter(s) tested ( "b" is common and the default, other common options are "sd" and "cor" ). This argument is not necessary, but can be handy to avoid having to specify the full names of the parameters.
- group : a string characterising the grouping factor to evaluate only group-level effects parameters.
- alpha : used to specify the width of the HDI (e.g. alpha = .05 for a 95% HDI)
- seed : seed for the random number generator to make the results reproducible.
The specification of the hypothesis argument is rather flexible. For example, we can test the (null) hypothesis that the slope of hate_groups_per_million equals 0 by specifying the hypothesis as "hate_groups_per_million = 0" :
This compares mod_regression to an alternative model where the prior for the slope of hate_groups_per_million is set to a point-prior at 0 (i.e. only the value 0 is allowed). The output of the function repeats some values that are also provided in the output of the summary() function (the posterior mean, standard deviation, and lower- and upper-bound of the 95% HDI). In addition, we find values of Evid.Ratio and Post.Prob . The Evidence Ratio ( Evid.Ratio ) is the value of the Bayes Factor \(\text{BF}_{01}\) comparing the model specified in the hypothesis (MODEl R) to the less restrictive MODEL G ( mod_regression ). So values larger than 1 indicate that the data provides evidence for the tested hypothesis (MODEL R) to MODEL G. Conversely, values smaller than 1 indicate evidence for MODEL G over MODEL R. The value found here ( \(\text{BF}_{01} = 0.1180559\) ) can be considered “moderate” evidence for MODEL G which allows hate_groups_per_million to have an effect, compared to MODEL R which fixes the effect to 0. The Bayes Factor in this procedure is calculated via the so-called Savage-Dickey density ratio ( Wagenmakers et al. 2010 ) . The Posterior Probability is the posterior probability that the hypothesis is true. For this point-hypothesis, this is the posterior probability of the model with the point-prior (MODEL R), assuming equal prior probabilities for this model and MODEL G.
Directional hypotheses can also be tested. For example, we can test the hypothesis that the slope of hate_groups_per_million is larger than 0 by specifying the hypothesis as "hate_groups_per_million > 0" :
Whilst the output is similar as before, for these directional tests, a different procedure is used to compute the “evidence ratio”. Here, the evidence ratio is the posterior probability that the parameter is larger than 0, divided by the posterior probability that the parameter value is smaller than 0, e.g.: \[\text{Evidence ratio} = \frac{p(\beta > 0|\text{data})}{p(\beta < 0|\text{data})}\] which is estimated simply by the proportion of posterior samples that are larger than 0 (which is also stated under Post.Prob ), divided by the proportion of posterior samples smaller than 0 (which equals \(1-\) Post.Prob ). You can also use the procedure to test some “wacky” hypotheses, such as that the slope of hate_groups_per_million is smaller than the slope of percent_bachelors_degree_or_higher :
As the scales of hate_groups_per_million and percent_bachelors_degree_or_higher are quite different, this hypotheses does not necessarily make too much sense from a scientific viewpoint. The example was mainly meant to show the flexibility of the procedure.
13.2.2 Using bridge sampling to obtain marginal likelihoods
Bridge sampling ( Bennett 1976 ; Meng and Wong 1996 ; Quentin F. Gronau et al. 2017 ) provides a general method to estimate the marginal likelihood from MCMC samples. We won’t go into the details of this algorithm here ( Quentin F. Gronau et al. 2017 provide a relatively readable introduction to this) , but note that it is a sampling-based approximation, and the accuracy of the method will depend on how many samples are used (and whether the MCMC algorithm has converged to sampling from the posterior distribution).
The implementation of bridge sampling in the bridgesampling , for which the brms::bridge_sampler() function provides a simple wrapper, requires that all parameters of the model are sampled at each step. This can be requested by setting the option save_pars = save_pars(all = TRUE) in the call to brms::brm() . We did not do this before, so to be able to use the brms::bridge_sampler() function, we should first re-estimate the model with:
Having set save_pars = save_pars(all = TRUE) , we can then call the brms::bridge_sampler() function on the estimated model as:
This function returns the approximate (natural) logarithm of the marginal likelihood, i.e. \[\widehat{\log p}(\text{data}|\text{MODEL})\] To compute a Bayes Factor, we will also need the (log) marginal likelihood for an alternative model. For example, we can set the prior for the slope of hate_groups_per_million to be a point-prior at 0 by specifying the prior distribution for that parameter as constant(0) :
We can now use the brms::bridge_sampler() function to compute the (log) marginal likelihood for this estimated model as:
We now have two (log) marginal likelihoods. To compute the actual Bayes Factor, we can use the factor that: \[\begin{aligned} \log \left( \frac{p(\text{data}|\text{MODEL 1})}{p(\text{data}|\text{MODEL 1})} \right) &= \log p(\text{data}|\text{MODEL 1}) - \log p(\text{data}|\text{MODEL 2}) \\ \frac{p(\text{data}|\text{MODEL 1})}{p(\text{data}|\text{MODEL 1})} &= \exp \left( \log p(\text{data}|\text{MODEL 1}) - \log p(\text{data}|\text{MODEL 2}) \right) \end{aligned}\] So we can compute the Bayes factor by taking the difference between the log marginal likelihoods, and then exponentiating:
where we have used that each object returned by the brms::bridge_sampler() is a list with the named element logml being equal to the (approximate) marginal log likelihood.
Using this explicit computation can be avoided by calling the bridgesampling::bf() function, which will provide the actual Bayes Factor from the log marginal likelihoods:
Curiously, a scaling factor of \(r = \tfrac{1}{2}\) in this case corresponds to a scaling factor of \(r = \tfrac{\sqrt{2}}{2}\) , which is something I don’t immediately understand, and will require further investigation. ↩︎

IMAGES
VIDEO
COMMENTS
To use and report a Bayesian hypothesis test, predicted effect sizes must be specified. The article will provide guidance in specifying effect sizes of interest (which also will be of relevance to those using frequentist statistics). First, if a minimally interesting effect size can be specified, a null interval is defined as the effects ...
The Bayes factor (sometimes abbreviated as BF) has a special place in the Bayesian hypothesis testing, because it serves a similar role to the p-value in orthodox hypothesis testing: it quantifies the strength of evidence provided by the data, and as such it is the Bayes factor that people tend to report when running a Bayesian hypothesis test ...
20.6.2.1 One-sided tests. We generally are less interested in testing against the null hypothesis of a specific point value (e.g. mean difference = 0) than we are in testing against a directional null hypothesis (e.g. that the difference is less than or equal to zero). We can also perform a directional (or one-sided) test using the results from ...
In Bayesian hypothesis testing, a one-sided hypothesis yields a more diagnostic test than a two-sided alternative (e.g., Jeffreys, 1961; Wetzels, Raaijmakers, Jakab, & Wagenmakers, 2009, p.283). ... Additionally, the robustness of the result to different prior distributions can be explored and included in the report. This is an important type ...
Bayesian hypothesis testing with Bayes factors is, at it's heart, a model comparison procedure. Bayesian models consist of a likelihood function and a prior distribution. A different prior distribution means a different model, and therefore a different result of the model comparison. ... Report the results. Make sure that you describe the ...
11. Bayesian hypothesis testing. This chapter introduces common Bayesian methods of testing what we could call statistical hypotheses . A statistical hypothesis is a hypothesis about a particular model parameter or a set of model parameters. Most often, such a hypothesis concerns one parameter, and the assumption in question is that this ...
Conceptualizing Hypothesis Testing via Bayes Factors. Bayesian inference is a fully probabilistic framework for drawing scientific conclusions that resembles how we naturally think about the world. Often, we hold an a priori position on a given issue. On a daily basis, we are confronted with facts about that issue.
If using model comparison or hypothesis testing as the basis for a decision, state and justify the decision threshold for the posterior model probability, and the minimum prior model probability that would make the posterior model probability exceed the decision threshold. ... How to use and report Bayesian hypothesis tests. Psychol. Conscious ...
Hypothesis Testing. Suppose we have univariate data y i iid ∼ N(θ, 1) goal is to test H0: θ = 0; vs H1: θ ≠ 0. Frequentist testing - likelihood ratio, Wald, score, UMP, confidence regions, etc. Need a test statistic T(y ( n)) T ( y ( n)) (and its sampling distribution) p-value: Calculate the probability of seeing a dataset/test ...
We first describe a standard Bayesian analysis of a single binomial response, going through the prior distribution choice and explaining how the posterior is calculated. We then discuss Bayesian hypothesis testing using the Bayes factor, a measure of how much the posterior odds of believing in one hypothesis changes from the prior odds.
In this chapter, you learnt about hypothesis testing using a Bayesian framework. The first two activities explored the logic of Bayesian statistics to make inferences and how it can be used to test hypotheses when expressed as the Bayes factor. ... This preprint outlines common errors and misconceptions when researcher report Bayes factors. 4.8 ...
We test the following hypotheses: H 0: δ = 0 versus H 1: δ ≠ 0. The following script of R code implements the Bayesian paired t -test and presents the p -value of the classical approach for comparison. The value r = 0.707 ( 2 / 2) denotes the scale of a Cauchy prior distribution of δ.
Again, we obtain a p-value less than 0.05, so we reject the null hypothesis. What does the Bayesian version of the t-test look like? Using the ttestBF() function, we can obtain a Bayesian analog of Student's independent samples t-test using the following command: ttestBF( formula = grade ~ tutor, data = harpo )
To use and report a Bayesian hypothesis test, predicted effect sizes must be specified. The article will provide guidance in specifying effect sizes of interest (which also will be of relevance to those using frequentist statistics). First, if a minimally interesting effect size can be specified, a null interval is defined as the effects ...
This article provides guidance on interpreting and reporting Bayesian hypothesis tests, in order to aid their understanding. To use and report a Bayesian hypothesis test, predicted effect sizes must be specified. The paper will provide guidance in specifying effect sizes of interest (which also will be of relevance to those using frequentist ...
discrepancy between the p-value and the objective Bayesian answers in precise hypothesis testing? Many Fisherians (and arguably Fisher) prefer likelihood ratios to p-values, when they are available (e.g., genetics). A lower bound on the Bayes factor (or likelihood ratio): choose π(θ) to be a point mass at θˆ, yielding B01(x) = Poisson(x j 0 ...
9.1.8 Bayesian Hypothesis Testing. Suppose that we need to decide between two hypotheses H0 H 0 and H1 H 1. In the Bayesian setting, we assume that we know prior probabilities of H0 H 0 and H1 H 1. That is, we know P(H0) = p0 P ( H 0) = p 0 and P(H1) = p1 P ( H 1) = p 1, where p0 + p1 = 1 p 0 + p 1 = 1. We observe the random variable (or the ...
In the context of Bayesian inference, hypothesis testing can be framed as a special case of model comparison where a model refers to a likelihood function and a prior distribution. Given two competing hypotheses and some relevant data, Bayesian hypothesis testing begins by specifying separate prior distributions to quantitatively describe each ...
To use and report a Bayesian hypothesis test, predicted effect sizes must be specified. The article will provide guidance in specifying effect sizes of interest (which also will be of relevance to those using frequentist statistics). First, if a minimally interesting effect size can be specified, a null interval is defined as the effects ...
To use and report a Bayesian hypothesis test, predicted effect sizes must be specified. The paper will provide guidance in specifying effect sizes of interest (which also will be of relevance to ...
To use and report a Bayesian hypothesis test, predicted effect sizes must be specified. The paper will provide guidance in specifying effect sizes of interest (which also will be of relevance to those using frequentist statistics). First, if a minimally interesting effect size can be specified, a null interval is defined as the effects smaller ...
13.1.1 A Bayesian one-sample t-test. A Bayesian alternative to a \(t\)-test is provided via the ttestBF function. Similar to the base R t.test function of the stats package, this function allows computation of a Bayes factor for a one-sample t-test or a two-sample t-tests (as well as a paired t-test, which we haven't covered in the course). Let's re-analyse the data we considered before ...
This normal-science and revolution pattern ties into a Bayesian workflow cycling between model building, inference, and model checking. The multiverse. The point of the "forking paths" metaphor in statistics is that multiple comparisons can be a problem, even when there is no "fishing expedition" or "p-hacking" and the research ...
Again, we obtain a p-value less than 0.05, so we reject the null hypothesis. What does the Bayesian version of the t-test look like? Using the ttestBF() function, we can obtain a Bayesian analog of Student's independent samples t-test using the following command: ttestBF( formula = grade ~ tutor, data = harpo )