
Assignment problem
1 formulation of the problem, 2 variants of the problem, 3 algorithms for solving the problem, 4 references.
Suppose that there are [math]n[/math] agents and [math]m[/math] tasks, which can be distributed between these agents. Only one task can be assigned to each agent, and each task can be assigned to only one agent. The cost of assignment of the [math]i[/math] -th task to the [math]j[/math] -th agent is [math]c(i, j)[/math] . If [math]c(i, j) = \infty[/math] , then the [math]i[/math] -th task cannot be assigned to the [math]j[/math] -th agent.
The assignment problem : find a feasible set of assignments [math]A = \{ (i_1, j_1), \ldots, (i_k, j_k) \}[/math] , [math]k = \min \{m, n\}[/math] having the maximum total cost:
If [math]m = n[/math] , then we say of the linear assignment problem : each agent is assigned to perform exactly one task, and each task is assigned to exactly one agent.
In the case of unit weights, we have to find a maximum matching in a bipartite graph, and the problem reduces to assigning as much tasks as possible.
- The Hungarian Method [1] [2] [3] for the linear problem. The complexity is [math]O(n^4)[/math] (and can be reduced [4] to [math]O(n^3)[/math] );
- the auction algorithm [5] [6] ;
- the Hopcroft-Karp algorithm [7] for the problem with unit weights. The complexity is [math]O(m \sqrt{n})[/math] .
- ↑ Kuhn, H W. “The Hungarian Method for the Assignment Problem.” Naval Research Logistics Quarterly 2, no. 1 (March 1955): 83–97. doi:10.1002/nav.3800020109.
- ↑ Kuhn, H W. “Variants of the Hungarian Method for Assignment Problems.” Naval Research Logistics Quarterly 3, no. 4 (December 1956): 253–58. doi:10.1002/nav.3800030404.
- ↑ Munkres, James. “Algorithms for the Assignment and Transportation Problems.” Journal of the Society for Industrial and Applied Mathematics 5, no. 1 (March 1957): 32–38. doi:10.1137/0105003.
- ↑ Tomizawa, N. “On Some Techniques Useful for Solution of Transportation Network Problems.” Networks 1, no. 2 (1971): 173–94. doi:10.1002/net.3230010206.
- ↑ Bertsekas, Dimitri P. “Auction Algorithms for Network Flow Problems: a Tutorial Introduction.” Computational Optimization and Applications 1 (1992): 7–66.
- ↑ Zavlanos, Michael M, Leonid Spesivtsev, and George J Pappas. “A Distributed Auction Algorithm for the Assignment Problem,” Proceedings of IEEE CDC'08, 1212–17, IEEE, 2008. doi:10.1109/CDC.2008.4739098.
- ↑ Hopcroft, John E, and Richard M Karp. “An $N^{5/2} $ Algorithm for Maximum Matchings in Bipartite Graphs.” SIAM Journal on Computing 2, no. 4 (1973): 225–31. doi:10.1137/0202019.
- Problem level
- Articles in progress
Navigation menu
Personal tools.
- Create account
- View source
- View history
- Recent changes
File storage
- Upload file
- What links here
- Related changes
- Special pages
- Printable version
- Permanent link
- Page information
- This page was last edited on 6 March 2018, at 17:08.
- Content is available under Creative Commons Attribution unless otherwise noted.
- Privacy policy
- About Algowiki
- Disclaimers
Please enable JavaScript to pass antispam protection! Here are the instructions how to enable JavaScript in your web browser http://www.enable-javascript.com . Antispam by CleanTalk.
Index Assignment problem Hungarian algorithm Solve online
The Hungarian algorithm: An example
We consider an example where four jobs (J1, J2, J3, and J4) need to be executed by four workers (W1, W2, W3, and W4), one job per worker. The matrix below shows the cost of assigning a certain worker to a certain job. The objective is to minimize the total cost of the assignment.
| 82 | 83 | 69 | 92 | |
| 77 | 37 | 49 | 92 | |
| 11 | 69 | 5 | 86 | |
| 8 | 9 | 98 | 23 |
Below we will explain the Hungarian algorithm using this example. Note that a general description of the algorithm can be found here .
Step 1: Subtract row minima
We start with subtracting the row minimum from each row. The smallest element in the first row is, for example, 69. Therefore, we substract 69 from each element in the first row. The resulting matrix is:
| 13 | 14 | 0 | 23 | (-69) | |
| 40 | 0 | 12 | 55 | (-37) | |
| 6 | 64 | 0 | 81 | (-5) | |
| 0 | 1 | 90 | 15 | (-8) |
Step 2: Subtract column minima
Similarly, we subtract the column minimum from each column, giving the following matrix:
| 13 | 14 | 0 | 8 | |
| 40 | 0 | 12 | 40 | |
| 6 | 64 | 0 | 66 | |
| 0 | 1 | 90 | 0 | |
| (-15) |
Step 3: Cover all zeros with a minimum number of lines
We will now determine the minimum number of lines (horizontal or vertical) that are required to cover all zeros in the matrix. All zeros can be covered using 3 lines:
| 13 | 14 | 0 | 8 | ||
| 40 | 0 | 12 | 40 | ||
| 6 | 64 | 0 | 66 | ||
| 0 | 1 | 90 | 0 | ||
Step 4: Create additional zeros
First, we find that the smallest uncovered number is 6. We subtract this number from all uncovered elements and add it to all elements that are covered twice. This results in the following matrix:
| 7 | 8 | 0 | 2 | |
| 40 | 0 | 18 | 40 | |
| 0 | 58 | 0 | 60 | |
| 0 | 1 | 96 | 0 |
Now we return to Step 3.
Again, We determine the minimum number of lines required to cover all zeros in the matrix. Now there are 4 lines required:
| 7 | 8 | 0 | 2 | ||
| 40 | 0 | 18 | 40 | ||
| 0 | 58 | 0 | 60 | ||
| 0 | 1 | 96 | 0 |
Because the number of lines required (4) equals the size of the matrix ( n =4), an optimal assignment exists among the zeros in the matrix. Therefore, the algorithm stops.
The optimal assignment
The following zeros cover an optimal assignment:
This corresponds to the following optimal assignment in the original cost matrix:
Thus, worker 1 should perform job 3, worker 2 job 2, worker 3 job 1, and worker 4 should perform job 4. The total cost of this optimal assignment is to 69 + 37 + 11 + 23 = 140.
Solve your own problem online
HungarianAlgorithm.com © 2013-2024
Solving assignment problem using min-cost-flow ¶
The assignment problem has two equivalent statements:
- Given a square matrix $A[1..N, 1..N]$ , you need to select $N$ elements in it so that exactly one element is selected in each row and column, and the sum of the values of these elements is the smallest.
- There are $N$ orders and $N$ machines. The cost of manufacturing on each machine is known for each order. Only one order can be performed on each machine. It is required to assign all orders to the machines so that the total cost is minimized.
Here we will consider the solution of the problem based on the algorithm for finding the minimum cost flow (min-cost-flow) , solving the assignment problem in $\mathcal{O}(N^3)$ .
Description ¶
Let's build a bipartite network: there is a source $S$ , a drain $T$ , in the first part there are $N$ vertices (corresponding to rows of the matrix, or orders), in the second there are also $N$ vertices (corresponding to the columns of the matrix, or machines). Between each vertex $i$ of the first set and each vertex $j$ of the second set, we draw an edge with bandwidth 1 and cost $A_{ij}$ . From the source $S$ we draw edges to all vertices $i$ of the first set with bandwidth 1 and cost 0. We draw an edge with bandwidth 1 and cost 0 from each vertex of the second set $j$ to the drain $T$ .
We find in the resulting network the maximum flow of the minimum cost. Obviously, the value of the flow will be $N$ . Further, for each vertex $i$ of the first segment there is exactly one vertex $j$ of the second segment, such that the flow $F_{ij}$ = 1. Finally, this is a one-to-one correspondence between the vertices of the first segment and the vertices of the second part, which is the solution to the problem (since the found flow has a minimal cost, then the sum of the costs of the selected edges will be the lowest possible, which is the optimality criterion).
The complexity of this solution of the assignment problem depends on the algorithm by which the search for the maximum flow of the minimum cost is performed. The complexity will be $\mathcal{O}(N^3)$ using Dijkstra or $\mathcal{O}(N^4)$ using Bellman-Ford . This is due to the fact that the flow is of size $O(N)$ and each iteration of Dijkstra algorithm can be performed in $O(N^2)$ , while it is $O(N^3)$ for Bellman-Ford.
Implementation ¶
The implementation given here is long, it can probably be significantly reduced. It uses the SPFA algorithm for finding shortest paths.
- Daili01 (75.89%)
- prpr (12.5%)
- Oleksandr Kulkov (7.14%)
- Shadab Zafar (2.68%)
- Jakob Kogler (0.89%)
- Hasan-Mesbaul-Ali-Taher (0.89%)
Algorithms: The Assignment Problem
One of the interesting things about studying optimization is that the techniques show up in a lot of different areas. The “assignment problem” is one that can be solved using simple techniques, at least for small problem sizes, and is easy to see how it could be applied to the real world.
Assignment Problem
Pretend for a moment that you are writing software for a famous ride sharing application. In a crowded environment, you might have multiple prospective customers that are requesting service at the same time, and nearby you have multiple drivers that can take them where they need to go. You want to assign the drivers to the customers in a way that minimizes customer wait time (so you keep the customers happy) and driver empty time (so you keep the drivers happy).
The assignment problem is designed for exactly this purpose. We start with m agents and n tasks. We make the rule that every agent has to be assigned to a task. For each agent-task pair, we figure out a cost associated to have that agent perform that task. We then figure out which assignment of agents to tasks minimizes the total cost.
Of course, it may be true that m != n , but that’s OK. If there are too many tasks, we can make up a “dummy” agent that is more expensive than any of the others. This will ensure that the least desirable task will be left to the dummy agent, and we can remove that from the solution. Or, if there are too many agents, we can make up a “dummy” task that is free for any agent. This will ensure that the agent with the highest true cost will get the dummy task, and will be idle.
If that last paragraph was a little dense, don’t worry; there’s an example coming that will help show how it works.
There are special algorithms for solving assignment problems, but one thing that’s nice about them is that a general-purpose solver can handle them too. Below is an example, but first it will help to cover a few concepts that we’ll be using.
Optimization Problems
Up above, we talked about making “rules” and minimizing costs. The usual name for this is optimization. An optimization problem is one where we have an “objective function” (which tells us what our goals are) and one or more “constraint functions” (which tell us what the rules are). The classic example is a factory that can make both “widgets” and “gadgets”. Each “widget” and “gadget” earns a certain amount of profit, but it also uses up raw material and time on the factory’s machines. The optimization problem is to determine exactly how many “widgets” and how many “gadgets” to make to maximize profit (the objective) while fitting within the material and time available (the constraints).
If we were to write this simple optimization problem out, it might look like this:
In this case, we have two variables: g for the number of gadgets we make and w for the number of widgets we make. We also have three constraints that we have to meet. Note that they are inequalities; we might not use all the available material or time in our optimal solution.
Just to unpack this a little: in English, the above is saying that we make 45 dollars / euros / quatloos per gadget we make. However, to make a gadget needs 120 lbs of raw material 1, 80 lbs of raw material 2, and 3.8 hours of machine time. So there is a limit on how many gadgets we can make, and it might be a better use of resources to balance gadgets with widgets.
Of course, real optimization problems have many more than two variables and many constraint functions, making them much harder to solve. The easiest kind of optimization problem to solve is linear, and fortunately, the assignment problem is linear.
Linear Programming
A linear program is a kind of optimization problem where both the objective function and the constraint functions are linear. (OK, that definition was a little self-referential.) We can have as many variables as we want, and as many constraint functions as we want, but none of the variables can have exponents in any of the functions. This limitation allows us to apply very efficient mathematical approaches to solve the problem, even for very large problems.
We can state the assignment problem as a linear programming problem. First, we choose to make “i” represent each of our agents (drivers) and “j” to represent each of our tasks (customers). Now, to write a problem like this, we need variables. The best approach is to use “indicator” variables, where xij = 1 means “driver i picks up customer j” and xij = 0 means “driver i does not pick up customer j”.
We wind up with:
This is a compact mathematical way to describe the problem, so again let me put it in English.
First, we need to figure out the cost of having each driver pick up each customer. Then, we can calculate the total cost for any scenario by just adding up the costs for the assignments we pick. For any assignment we don’t pick, xij will equal zero, so that term will just drop out of the sum.
Of course, the way we set up the objective function, the cheapest solution is for no drivers to pick up any customers. That’s not a very good business model. So we need a constraint to show that we want to have a driver assigned to every customer. At the same time, we can’t have a driver assigned to mutiple customers. So we need a constraint for that too. That leads us to the two constraints in the problem. The first just says, if you add up all the assignments for a given driver, you want the total number of assignments for that driver to be exactly one. The second constraint says, if you add up all the assignments to a given customer, you want the total number of drivers assigned to the customer to be one. If you have both of these, then each driver is assigned to exactly one customer, and the customers and drivers are happy. If you do it in a way that minimizes costs, then the business is happy too.
Solving with Octave and GLPK
The GNU Linear Programming Kit is a library that solves exactly these kinds of problems. It’s easy to set up the objective and constraints using GNU Octave and pass these over to GLPK for a solution.
Given some made-up sample data, the program looks like this:
Start with the definition of “c”, the cost information. For this example, I chose to have four drivers and three customers. There are sixteen numbers there; the first four are the cost of each driver to get the first customer, the next four are for the second customer, and the next four are for the third customer. Because we have an extra driver, we add a “dummy” customer at the end that is zero cost. This represents one of the drivers being idle.
The next definition is “b”, the right-hand side of our constraints. There are eight constraints, one for each of the drivers, and one for each of the customers (including the dummy). For each constraint, the right-hand side is 1.
The big block in the middle defines our constraint matrix “a”. This is the most challenging part of taking the mathematical definition and putting it into a form that is usable by GLPK; we have to expand out each constraint. Fortunately, in these kinds of cases, we tend to get pretty patterns that help us know we’re on the right track.
The first line in “a” says that the first customer needs a driver. To see why, remember that in our cost information, the first four numbers are the cost for each driver to get the first customer. With this constraint, we are requiring that one of those four costs be included and therefore that a driver is “selected” for the first customer. The other lines in “a” work similarly; the last four ensure that each driver has an assignment.
Note that the number of rows in “a” matches the number of items in “b”, and the number of columns in “a” matches the number of items in “c”. This is important; GLPK won’t run if this is not true (and our problem isn’t stated right in any case).
Compared to the above, the last few lines are easy.
- “lb” gives the lower bound for each variable.
- “ub” gives the upper bound.
- “ctype” tells GLPK that each constraint is an equality (“strict” as opposed to providing a lower or upper bound).
- “vartype” tells GLPK that these variables are all integers (can’t have half a driver showing up).
- “s” tells GLPK that we want to minimize our costs, not maximize them.
We push all that through a function call to GLPK, and what comes back are two values (along with some other stuff I’ll exclude for clarity):
The first item tells us that our best solution takes 27 minutes, or dollars, or whatever unit we used for cost. The second item tells us the assignments we got. (Note for pedants: I transposed this output to save space.)
This output tells us that customer 1 gets driver 2, customer 2 gets driver 3, customer 3 gets driver 4, and driver 1 is idle. If you look back at the cost data, you can see this makes sense, because driver 1 had some of the most expensive times to the three customers. You can also see that it managed to pick the least expensive pairing for each customer. (Of course, if I had done a better job making up cost data, it might not have picked the least expensive pairing in all cases, because a suboptimal individual pairing might still lead to an overall optimal solution. But this is a toy example.)
Of course, for a real application, we would have to take into consideration many other factors, such as the passage of time. Rather than knowing all of our customers and drivers up front, we would have customers and drivers continually showing up and being assigned. But I hope this simple example has revealed some of the concepts behind optimization and linear programming and the kinds of real-world problems that can be solved.
- DOI: 10.1287/inte.2023.0084
- Corpus ID: 267561033
Meituan's Real-Time Intelligent Dispatching Algorithms Build the World's Largest Minute-Level Delivery Network
- Yile Liang , Haocheng Luo , +20 authors Ling Wang
- Published in INFORMS J. Appl. Anal. 1 January 2024
- Business, Computer Science
- INFORMS J. Appl. Anal.
3 References
Algorithms for the assignment and transiortation troblems*, the hungarian method for the assignment problem, graph representation learning, related papers.
Showing 1 through 3 of 0 Related Papers
Help | Advanced Search
Mathematics > Optimization and Control
Title: a fast single-loop primal-dual algorithm for non-convex functional constrained optimization.
Abstract: Non-convex functional constrained optimization problems have gained substantial attention in machine learning and signal processing. This paper develops a new primal-dual algorithm for solving this class of problems. The algorithm is based on a novel form of the Lagrangian function, termed {\em Proximal-Perturbed Augmented Lagrangian}, which enables us to develop an efficient and simple first-order algorithm that converges to a stationary solution under mild conditions. Our method has several key features of differentiation over existing augmented Lagrangian-based methods: (i) it is a single-loop algorithm that does not require the continuous adjustment of the penalty parameter to infinity; (ii) it can achieves an improved iteration complexity of $\widetilde{\mathcal{O}}(1/\epsilon^2)$ or at least ${\mathcal{O}}(1/\epsilon^{2/q})$ with $q \in (2/3,1)$ for computing an $\epsilon$-approximate stationary solution, compared to the best-known complexity of $\mathcal{O}(1/\epsilon^3)$; and (iii) it effectively handles functional constraints for feasibility guarantees with fixed parameters, without imposing boundedness assumptions on the dual iterates and the penalty parameters. We validate the effectiveness of our method through numerical experiments on popular non-convex problems.
| Subjects: | Optimization and Control (math.OC) |
| Cite as: | [math.OC] |
| (or [math.OC] for this version) | |
| Focus to learn more arXiv-issued DOI via DataCite |
Submission history
Access paper:.
- HTML (experimental)
- Other Formats
References & Citations
- Google Scholar
- Semantic Scholar
BibTeX formatted citation
Bibliographic and Citation Tools
Code, data and media associated with this article, recommenders and search tools.
- Institution
arXivLabs: experimental projects with community collaborators
arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.
Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.
Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .
- Data Structures
- Linked List
- Binary Tree
- Binary Search Tree
- Segment Tree
- Disjoint Set Union
- Fenwick Tree
- Red-Black Tree
- Advanced Data Structures
- Hashing in Data Structure
Introduction to Hashing
What is hashing.
- Index Mapping (or Trivial Hashing) with negatives allowed
- Separate Chaining Collision Handling Technique in Hashing
- Open Addressing Collision Handling technique in Hashing
- Double Hashing
- Load Factor and Rehashing
Easy problems on Hashing
- Find whether an array is subset of another array
- Union and Intersection of two Linked List using Hashing
- Pair with given Sum (Two Sum)
- Maximum distance between two occurrences of same element in array
- Most frequent element in an array
- Find the only repetitive element between 1 to N-1
- How to check if two given sets are disjoint?
- Non-overlapping sum of two sets
- Check if two arrays are equal or not
- Find missing elements of a range
- Minimum number of subsets with distinct elements
- Remove minimum number of elements such that no common element exist in both array
- Count pairs with given sum
- Count quadruples from four sorted arrays whose sum is equal to a given value x
- Sort elements by frequency | Set 4 (Efficient approach using hash)
- Find all pairs (a, b) in an array such that a % b = k
- Group words with same set of characters
- k-th distinct (or non-repeating) element among unique elements in an array.
Intermediate problems on Hashing
- Find Itinerary from a given list of tickets
- Find number of Employees Under every Manager
- Longest subarray with sum divisible by K
- Find the length of largest subarray with 0 sum
- Longest Increasing consecutive subsequence
- Count distinct elements in every window of size k
- Design a data structure that supports insert, delete, search and getRandom in constant time
- Find subarray with given sum | Set 2 (Handles Negative Numbers)
- Implementing our Own Hash Table with Separate Chaining in Java
- Implementing own Hash Table with Open Addressing Linear Probing
- Maximum possible difference of two subsets of an array
- Sorting using trivial hash function
- Smallest subarray with k distinct numbers
Hard problems on Hashing
- Clone a Binary Tree with Random Pointers
- Largest subarray with equal number of 0s and 1s
- All unique triplets that sum up to a given value
- Range Queries for Frequencies of array elements
- Elements to be added so that all elements of a range are present in array
- Cuckoo Hashing - Worst case O(1) Lookup!
- Count subarrays having total distinct elements same as original array
- Maximum array from two given arrays keeping order same
- Find Sum of all unique sub-array sum for a given array.
- Length of longest strict bitonic subsequence
- Find All Duplicate Subtrees
- Find if there is a rectangle in binary matrix with corners as 1
- Top 20 Hashing Technique based Interview Questions
Hashing refers to the process of generating a fixed-size output from an input of variable size using the mathematical formulas known as hash functions. This technique determines an index or location for the storage of an item in a data structure.
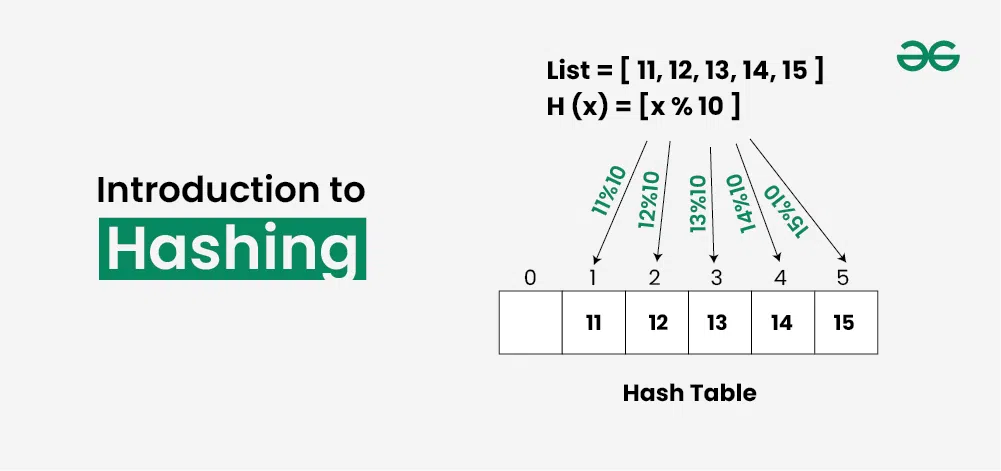
Table of Content
Need for Hash data structure
Components of hashing, how does hashing work, what is a hash function.
- Types of Hash functions
Properties of a Good hash function
Complexity of calculating hash value using the hash function, problem with hashing, what is collision, how to handle collisions.
- Separate Chaining
- Linear Probing
- Quadratic Probing

What is meant by Load Factor in Hashing?
What is rehashing, applications of hash data structure, real-time applications of hash data structure, advantages of hash data structure, disadvantages of hash data structure.
- Frequently Asked Questions(FAQs) on Hashing
Hashing in Data Structures refers to the process of transforming a given key to another value. It involves mapping data to a specific index in a hash table using a hash function that enables fast retrieval of information based on its key. The transformation of a key to the corresponding value is done using a Hash Function and the value obtained from the hash function is called Hash Code .
Every day, the data on the internet is increasing multifold and it is always a struggle to store this data efficiently. In day-to-day programming, this amount of data might not be that big, but still, it needs to be stored, accessed, and processed easily and efficiently. A very common data structure that is used for such a purpose is the Array data structure.
Now the question arises if Array was already there, what was the need for a new data structure! The answer to this is in the word ” efficiency “. Though storing in Array takes O(1) time, searching in it takes at least O(log n) time. This time appears to be small, but for a large data set, it can cause a lot of problems and this, in turn, makes the Array data structure inefficient.
So now we are looking for a data structure that can store the data and search in it in constant time, i.e. in O(1) time. This is how Hashing data structure came into play. With the introduction of the Hash data structure, it is now possible to easily store data in constant time and retrieve them in constant time as well.
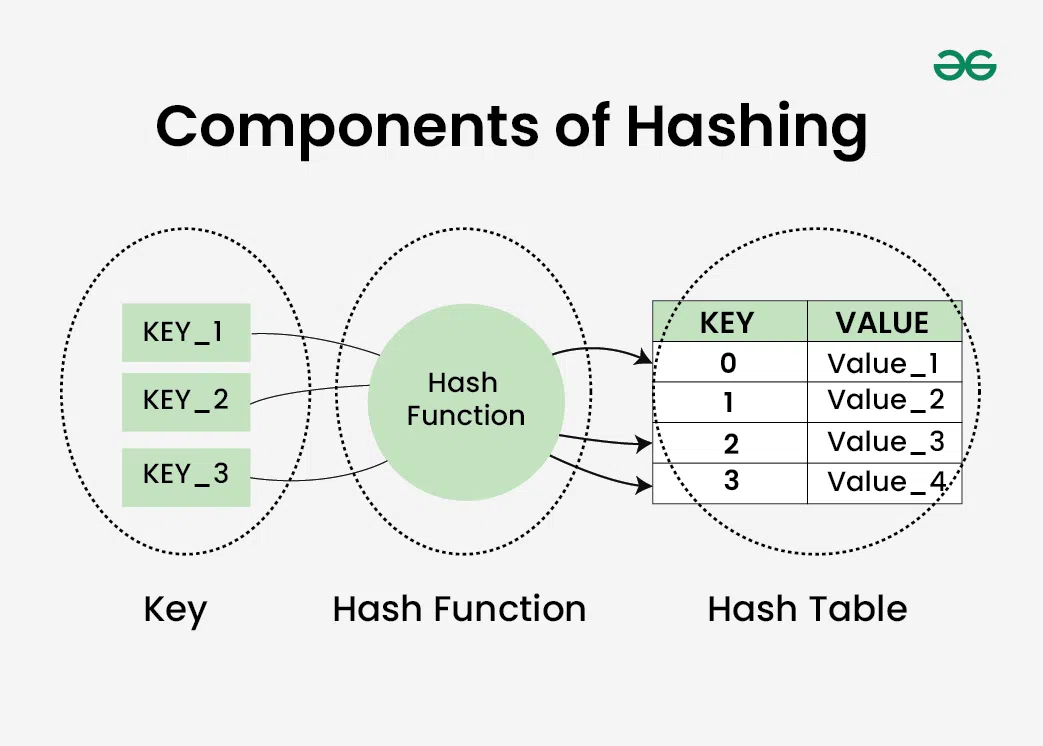
There are majorly three components of hashing:
- Key: A Key can be anything string or integer which is fed as input in the hash function the technique that determines an index or location for storage of an item in a data structure.
- Hash Function: The hash function receives the input key and returns the index of an element in an array called a hash table. The index is known as the hash index .
- Hash Table: Hash table is a data structure that maps keys to values using a special function called a hash function. Hash stores the data in an associative manner in an array where each data value has its own unique index.
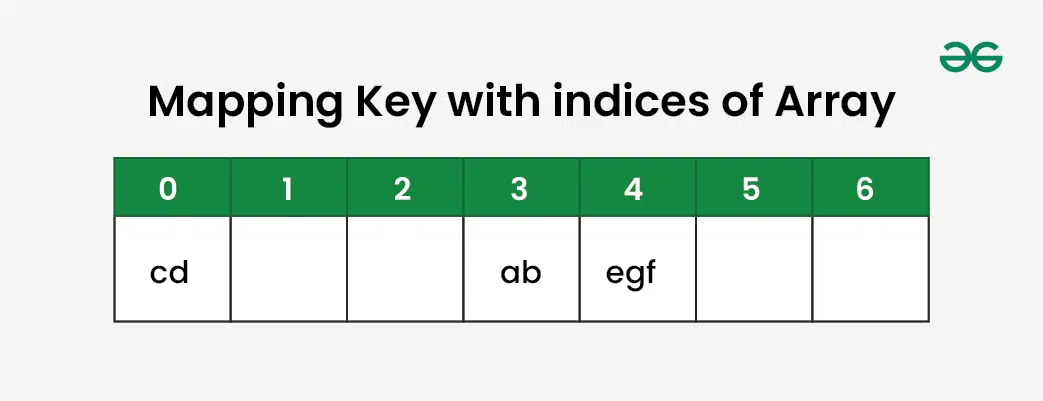
Suppose we have a set of strings {“ab”, “cd”, “efg”} and we would like to store it in a table.
Our main objective here is to search or update the values stored in the table quickly in O(1) time and we are not concerned about the ordering of strings in the table. So the given set of strings can act as a key and the string itself will act as the value of the string but how to store the value corresponding to the key?
- Step 1: We know that hash functions (which is some mathematical formula) are used to calculate the hash value which acts as the index of the data structure where the value will be stored.
- “b”=2, .. etc, to all alphabetical characters.
- Step 3: Therefore, the numerical value by summation of all characters of the string:
“ab” = 1 + 2 = 3, “cd” = 3 + 4 = 7 , “efg” = 5 + 6 + 7 = 18
- Step 4: Now, assume that we have a table of size 7 to store these strings. The hash function that is used here is the sum of the characters in key mod Table size . We can compute the location of the string in the array by taking the sum(string) mod 7 .
- “ab” in 3 mod 7 = 3,
- “cd” in 7 mod 7 = 0, and
- “efg” in 18 mod 7 = 4.
The above technique enables us to calculate the location of a given string by using a simple hash function and rapidly find the value that is stored in that location. Therefore the idea of hashing seems like a great way to store (key, value) pairs of the data in a table.
The hash function creates a mapping between key and value, this is done through the use of mathematical formulas known as hash functions. The result of the hash function is referred to as a hash value or hash. The hash value is a representation of the original string of characters but usually smaller than the original.
For example: Consider an array as a Map where the key is the index and the value is the value at that index. So for an array A if we have index i which will be treated as the key then we can find the value by simply looking at the value at A[i].
Types of Hash functions:
There are many hash functions that use numeric or alphanumeric keys. This article focuses on discussing different hash functions :
- Division Method.
- Mid Square Method
- Folding Method.
- Multiplication Method
A hash function that maps every item into its own unique slot is known as a perfect hash function. We can construct a perfect hash function if we know the items and the collection will never change but the problem is that there is no systematic way to construct a perfect hash function given an arbitrary collection of items. Fortunately, we will still gain performance efficiency even if the hash function isn’t perfect. We can achieve a perfect hash function by increasing the size of the hash table so that every possible value can be accommodated. As a result, each item will have a unique slot. Although this approach is feasible for a small number of items, it is not practical when the number of possibilities is large.
So, We can construct our hash function to do the same but the things that we must be careful about while constructing our own hash function.
A good hash function should have the following properties:
- Efficiently computable.
- Should uniformly distribute the keys (Each table position is equally likely for each.
- Should minimize collisions.
- Should have a low load factor(number of items in the table divided by the size of the table).
- Time complexity: O(n)
- Space complexity: O(1)
If we consider the above example, the hash function we used is the sum of the letters, but if we examined the hash function closely then the problem can be easily visualized that for different strings same hash value is begin generated by the hash function.
For example: {“ab”, “ba”} both have the same hash value, and string {“cd”,”be”} also generate the same hash value, etc. This is known as collision and it creates problem in searching, insertion, deletion, and updating of value.
Collision in Hashing occurs when two different keys map to the same hash value. Hash collisions can be intentionally created for many hash algorithms. The probability of a hash collision depends on the size of the algorithm, the distribution of hash values and the efficiency of Hash function.
The hashing process generates a small number for a big key, so there is a possibility that two keys could produce the same value. The situation where the newly inserted key maps to an already occupied, and it must be handled using some collision handling technology.
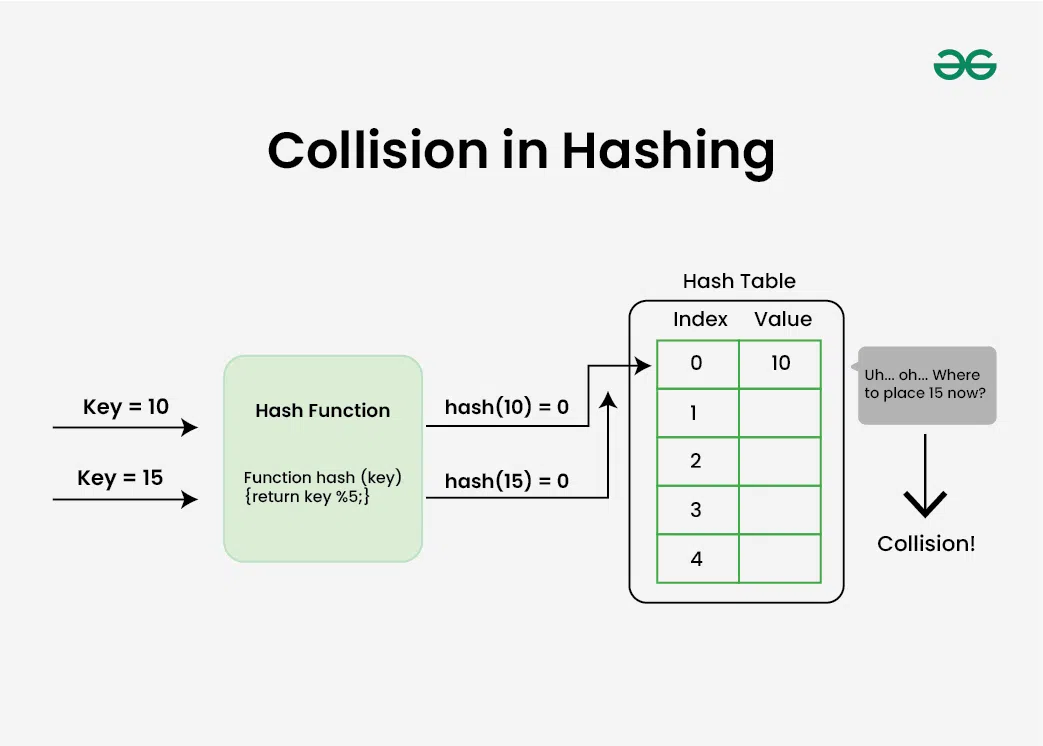
There are mainly two methods to handle collision:
- Open Addressing

1) Separate Chaining
The idea is to make each cell of the hash table point to a linked list of records that have the same hash function value. Chaining is simple but requires additional memory outside the table.
Example: We have given a hash function and we have to insert some elements in the hash table using a separate chaining method for collision resolution technique.
Let’s see step by step approach to how to solve the above problem:
Hence In this way, the separate chaining method is used as the collision resolution technique.
2) Open Addressing
In open addressing, all elements are stored in the hash table itself. Each table entry contains either a record or NIL. When searching for an element, we examine the table slots one by one until the desired element is found or it is clear that the element is not in the table.
2.a) Linear Probing
In linear probing, the hash table is searched sequentially that starts from the original location of the hash. If in case the location that we get is already occupied, then we check for the next location.
Calculate the hash key. i.e. key = data % size Check, if hashTable[key] is empty store the value directly by hashTable[key] = data If the hash index already has some value then check for next index using key = (key+1) % size Check, if the next index is available hashTable[key] then store the value. Otherwise try for next index. Do the above process till we find the space.
Example: Let us consider a simple hash function as “key mod 5” and a sequence of keys that are to be inserted are 50, 70, 76, 85, 93.
2.b) Quadratic Probing
Quadratic probing is an open addressing scheme in computer programming for resolving hash collisions in hash tables. Quadratic probing operates by taking the original hash index and adding successive values of an arbitrary quadratic polynomial until an open slot is found.
An example sequence using quadratic probing is:
H + 1 2 , H + 2 2 , H + 3 2 , H + 4 2 …………………. H + k 2
This method is also known as the mid-square method because in this method we look for i 2 ‘th probe (slot) in i’th iteration and the value of i = 0, 1, . . . n – 1. We always start from the original hash location. If only the location is occupied then we check the other slots.
Let hash(x) be the slot index computed using the hash function and n be the size of the hash table.
If the slot hash(x) % n is full, then we try (hash(x) + 1 2 ) % n. If (hash(x) + 1 2 ) % n is also full, then we try (hash(x) + 2 2 ) % n. If (hash(x) + 2 2 ) % n is also full, then we try (hash(x) + 3 2 ) % n. This process will be repeated for all the values of i until an empty slot is found
Example: Let us consider table Size = 7, hash function as Hash(x) = x % 7 and collision resolution strategy to be f(i) = i 2 . Insert = 22, 30, and 50
2.c) Double Hashing
Double hashing is a collision resolving technique in Open Addressed Hash tables. Double hashing make use of two hash function,
- The first hash function is h1(k) which takes the key and gives out a location on the hash table. But if the new location is not occupied or empty then we can easily place our key.
- But in case the location is occupied (collision) we will use secondary hash-function h2(k) in combination with the first hash-function h1(k) to find the new location on the hash table.
This combination of hash functions is of the form
- i is a non-negative integer that indicates a collision number,
- k = element/key which is being hashed
- n = hash table size.
Complexity of the Double hashing algorithm:
Example: Insert the keys 27, 43, 692, 72 into the Hash Table of size 7. where first hash-function is h1(k) = k mod 7 and second hash-function is h2(k) = 1 + (k mod 5)
The load factor of the hash table can be defined as the number of items the hash table contains divided by the size of the hash table. Load factor is the decisive parameter that is used when we want to rehash the previous hash function or want to add more elements to the existing hash table.
It helps us in determining the efficiency of the hash function i.e. it tells whether the hash function which we are using is distributing the keys uniformly or not in the hash table.
As the name suggests, rehashing means hashing again. Basically, when the load factor increases to more than its predefined value (the default value of the load factor is 0.75), the complexity increases. So to overcome this, the size of the array is increased (doubled) and all the values are hashed again and stored in the new double-sized array to maintain a low load factor and low complexity.
- Hash is used in databases for indexing.
- Hash is used in disk-based data structures.
- In some programming languages like Python, JavaScript hash is used to implement objects.
- Hash is used for cache mapping for fast access to the data.
- Hash can be used for password verification.
- Hash is used in cryptography as a message digest.
- Rabin-Karp algorithm for pattern matching in a string.
- Calculating the number of different substrings of a string.
- Hash provides better synchronization than other data structures.
- Hash tables are more efficient than search trees or other data structures
- Hash provides constant time for searching, insertion, and deletion operations on average.
- Hash is inefficient when there are many collisions.
- Hash collisions are practically not avoided for a large set of possible keys.
- Hash does not allow null values.
Frequently Asked Questions(FAQs) on Hashing:
1. what is a hash function.
Hashing refers to the process of transforming a given key to another value. It involves mapping data to a specific index in a hash table using a hash function that enables fast retrieval of information based on its key.
2. What is a Hash function?
Hash function is a function that takes an input and return a fixed-size string of bytes. The hash function receives the input key and returns the index of an element in an array called a hash table. The index is known as the hash index.
3. What are Hash collisions?
Hash collisions occur when two different inputs passed to the hash function produce the same hash value. The lesser the number of hash collisions, the better the hash function is.
4. What are hash tables?
Hash tables are data structures that use hash functions to map keys to values, allowing for efficient retrieval of data when needed. Hash table maps keys to values using a special function called a hash function. Hash stores the data in an associative manner in an array where each data value has its own unique index.
5. What are some applications of Hashing?
Hashing is used in databases for indexing, disk-based data structures and data compression algorithms. Hashing is also used to store passwords securely by applying a hash function to the password and storing the hashed result, rather than the plain text password.
From the above discussion, we conclude that the goal of hashing is to resolve the challenge of finding an item quickly in a collection. For example, if we have a list of millions of English words and we wish to find a particular term then we would use hashing to locate and find it more efficiently. It would be inefficient to check each item on the millions of lists until we find a match. Hashing reduces search time by restricting the search to a smaller set of words at the beginning.
Please Login to comment...
Similar reads.
- DSA Tutorials
Improve your Coding Skills with Practice
What kind of Experience do you want to share?

- Advanced Search
RevAP: : A bankruptcy-based algorithm to solve the multi-agent credit assignment problem in task start threshold-based multi-agent systems
New citation alert added.
This alert has been successfully added and will be sent to:
You will be notified whenever a record that you have chosen has been cited.
To manage your alert preferences, click on the button below.
New Citation Alert!
Please log in to your account
Information & Contributors
Bibliometrics & citations, view options, recommendations, multi-agent reinforcement learning by the actor-critic model with an attention interface.
Multi-agent reinforcement learning algorithms have achieved satisfactory performances in various scenarios, but many of them encounter difficulties in partially observable environments. In partially observable environments, the ...
Toward a Solution to Multi-agent Credit Assignment Problem
Multi-agent systems (MAS) try to formulate dynamic world which surround human being in every aspect of his life. One of the important challenges encountered in multiagent systems is the credit assignment problem, simply means distributing the result of ...
Deep Implicit Coordination Graphs for Multi-agent Reinforcement Learning
Multi-agent reinforcement learning (MARL) requires coordination to efficiently solve certain tasks. Fully centralized control is often infeasible in such domains due to the size of joint action spaces. Coordination graph based formalization allows ...
Information
Published in.
North-Holland Publishing Co.
Netherlands
Publication History
Author tags.
- Multi-agent system
- Credit assignment problem
- Bankruptcy problem
- Multi-agent reinforcement learning
- Cooperative game theory
- Research-article
Contributors
Other metrics, bibliometrics, article metrics.
- 0 Total Citations
- 0 Total Downloads
- Downloads (Last 12 months) 0
- Downloads (Last 6 weeks) 0
View options
Login options.
Check if you have access through your login credentials or your institution to get full access on this article.
Full Access
Share this publication link.
Copying failed.
Share on social media
Affiliations, export citations.
- Please download or close your previous search result export first before starting a new bulk export. Preview is not available. By clicking download, a status dialog will open to start the export process. The process may take a few minutes but once it finishes a file will be downloadable from your browser. You may continue to browse the DL while the export process is in progress. Download
- Download citation
- Copy citation
We are preparing your search results for download ...
We will inform you here when the file is ready.
Your file of search results citations is now ready.
Your search export query has expired. Please try again.
Research on optimization of multimodal hub-and-spoke transport network under uncertain demand
- Zhang, Jianpeng
- Li, Yuanping
In the cargo transportation system, the hub-and-spoke transport network can make full use of the scale effect between logistics hubs and reduce logistics costs. Joint transportation of multiple modes of transportation can give full play to the advantages of different modes of transportation, which not only reduces logistics costs but also improves transportation efficiency. Therefore, this paper combines the advantages of multimodal transportation and hub-and-spoke network, and establishes an optimization model of multimodal hub-and-spoke transport network under demand uncertainty. The model takes into account hub capacity constraints and customer satisfaction with respect to transportation time, and to facilitate the model solution, we utilize the fuzzy expected value method and the fuzzy chance constraints based on credibility to clarify the uncertain variables in the model. We use mixed coding to describe the selection of hubs, assignment of nodes, and choice of transportation modes in this study and use the NSGA-II algorithm with local reinforcement to solve the problem. Finally, numerical experiments are designed to verify the validity of the model and algorithm through sensitivity analysis of relevant parameters, determine the reasonable number of hubs and confidence level, and obtain the influence of the change of hub capacity limit and the ratio of single and double hub transit on the research objectives. The results show that: the NSGA-II algorithm with local reinforcement can significantly improve the convergence speed of the algorithm; There is benefit inversion between economic cost and time cost, and the pursuit of economic cost minimization and time cost minimization, respectively, will lead to different choices of the number of hubs; Increasing the ratio of goods transfer between hubs is beneficial for fully utilizing the scale effect between hubs, achieving the goal of reducing economic costs, but at the same time, it will increase time costs.

COMMENTS
Time complexity : O(n^3), where n is the number of workers and jobs. This is because the algorithm implements the Hungarian algorithm, which is known to have a time complexity of O(n^3). Space complexity : O(n^2), where n is the number of workers and jobs.This is because the algorithm uses a 2D cost matrix of size n x n to store the costs of assigning each worker to a job, and additional ...
The assignment problem is a fundamental combinatorial optimization problem. In its most general form, the problem is as follows: The problem instance has a number of agents and a number of tasks. Any agent can be assigned to perform any task, incurring some cost that may vary depending on the agent-task assignment.
The Hungarian method is a combinatorial optimization algorithm that solves the assignment problem in polynomial time and which anticipated later primal-dual methods.It was developed and published in 1955 by Harold Kuhn, who gave it the name "Hungarian method" because the algorithm was largely based on the earlier works of two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry.
The assignment problem is a special case of the transportation problem, which in turn is a special case of the min-cost flow problem, so it can be solved using algorithms that solve the more general cases. Also, our problem is a special case of binary integer linear programming problem (which is NP-hard). But, due to the specifics of the ...
Hungarian algorithm steps for minimization problem. Step 1: For each row, subtract the minimum number in that row from all numbers in that row. Step 2: For each column, subtract the minimum number in that column from all numbers in that column. Step 3: Draw the minimum number of lines to cover all zeroes.
Solution 2: Hungarian Algorithm The optimal assignment can be found using the Hungarian algorithm. The Hungarian algorithm has worst case run-time complexity of O(n^3). Solution 3: DFS/BFS on state space tree A state space tree is a N-ary tree with property that any path from root to leaf node holds one of many solutions to given problem.
0 2000 500. Step 2: Subtract minimum of every column. 0, 1500 and 0 are subtracted from columns 1, 2 and 3 respectively. 0 0 1000. 500 1000 0. 0 500 500. Step 3: Cover all zeroes with minimum number of horizontal and vertical lines. Step 4: Since we need 3 lines to cover all zeroes, the optimal assignment is found.
THE HUNGARIAN METHOD FOR THE ASSIGNMENT. PROBLEM'. H. W. Kuhn. Bryn Y a w College. Assuming that numerical scores are available for the perform- ance of each of n persons on each of n jobs, the "assignment problem" is the quest for an assignment of persons to jobs so that the sum of the. n scores so obtained is as large as possible.
The assignment problem is one of the fundamental combinatorial optimization problems in the branch of optimization or operations research in mathematics. ... Simplex Algorithm adapted to solve network problems The Simplex Algorithm is a general purpose algorithm to find the maximum/minimum of a linear cost function with linear constraints.
In the case of unit weights, we have to find a maximum matching in a bipartite graph, and the problem reduces to assigning as much tasks as possible. 3 Algorithms for solving the problem. The Hungarian Method for the linear problem. The complexity is [math]O(n^4)[/math] (and can be reduced to [math]O(n^3)[/math]); the auction algorithm;
whereby the assignment optimization is viewed as the primal problem and the minimization of the cost (1.2)-(1.3) is the dual problem.y Algorithms for Solving the Assignment Problem There are several iterative algorithms for the solution of the assignment problem, which are described in
Total Cost= 2+8+4+6=20. Approach 3: Greedy Approach In this case, the algorithm will choose the lowest cost worker to be assigned to the task as the first assignment, then choose the next lowest ...
The algorithm maintains a matching M and compatible prices p. Pf. Follows from Lemmas 2 and 3 and initial choice of prices. ! Theorem. The algorithm returns a min cost perfect matching. Pf. Upon termination M is a perfect matching, and p are compatible Optimality follows from Observation 2. ! Theorem. The algorithm can be implemented in O(n 3 ...
The Assignment Problem and the Hungarian Method 1. Example 1: You work as a sales manager for a toy manufacturer, and you currently have three salespeople on ... The following algorithm applies the above theorem to a given n × n cost matrix to find an optimal assignment. Step 1. Subtract the smallest entry in each row from all the entries of its
The classical solution to the assignment problem is given by the Hungarian or Kuhn-Munkres algorithm, originally proposed by H. W. Kuhn in 1955 [3] and refined by J. Munkres in 1957 [5]. The Hungarian algorithm solves the assignment problem in O(n3) time, where n is the size of one partition of the bipartite graph. This and other
The assignment problem deals with assigning machines to tasks, workers to jobs, soccer players to positions, and so on. The goal is to determine the optimum assignment that, for example, minimizes the total cost or maximizes the team effectiveness. The assignment problem is a fundamental problem in the area of combinatorial optimization.
The Hungarian algorithm: An example. We consider an example where four jobs (J1, J2, J3, and J4) need to be executed by four workers (W1, W2, W3, and W4), one job per worker. The matrix below shows the cost of assigning a certain worker to a certain job. The objective is to minimize the total cost of the assignment.
Massachusetts Technology, MA Cambridge, 02139, U.S.A. and. Institute of. Received 15 August 1979 Revised manuscript 1980 received 6 October. Wepropose new algorithm a for the classical assignment problem. in some ways the Hungarian in method o er but respects. The av differs rag computational of an complexity effic ent of implementation the a ...
The following algorithm is known as the successive shortest path algorithm for the assignment problem. Algorithm SSP begin x = 0; while some node is free do begin select an origin node i; in the residual network, find the minimum cost augmenting path P from i to some free destination node t; augment along the path P;
The complexity of this solution of the assignment problem depends on the algorithm by which the search for the maximum flow of the minimum cost is performed. The complexity will be $\mathcal{O}(N^3)$ using Dijkstra or $\mathcal{O}(N^4)$ using Bellman-Ford.
a column of C, we will not change the optimal solu. ion.Observation 2. Consider an assignment problem with cost matrix C. If C 0, and there exists an assignmen. which only assigns i to j if cij = 0, then this assigment is optimal.These two observations give us an idea for an algorithm: we subtract the minimu.
One of the interesting things about studying optimization is that the techniques show up in a lot of different areas. The "assignment problem" is one that can be solved using simple techniques, at least for small problem sizes, and is easy to see how it could be applied to the real world. Assignment Problem Pretend for a moment that you are writing software for a famous ride sharing ...
A Distributed Algorithm for the Assignment Problem Dimitri P. Bertsekas March 1979y Abstract This paper describes a new algorithm for solving the classical assign-ment problem. The algorithm is of a primal-dual nature and in some ways resembles the Hungarian and subgradient methods, but is substantially di erent in other respects.
In the assignment problem, a set of items must be allocated to unit-demand agents who express ordinal preferences (rankings) over the items. In the assignment problem with priorities, agents with higher priority are entitled to their preferred goods with respect to lower priority agents. ... We describe two algorithms, Cycle Elimination (CE ...
Cuban emphasized the power of algorithms by stating, "The person who controls the algorithm controls the world." He explained that these algorithms dictate the content users see, effectively ...
Meituan's state-of-the-art real-time intelligent dispatch system harnesses the power of operations research and machine learning algorithms to fine-tune order assignments, simultaneously addressing the needs of consumers, couriers, merchants, and the platform itself. Over the past decade, Meituan, China's premier online food delivery (OFD) platform, has witnessed remarkable growth. Central ...
Non-convex functional constrained optimization problems have gained substantial attention in machine learning and signal processing. This paper develops a new primal-dual algorithm for solving this class of problems. The algorithm is based on a novel form of the Lagrangian function, termed {\\em Proximal-Perturbed Augmented Lagrangian}, which enables us to develop an efficient and simple first ...
This is known as collision and it creates problem in searching, insertion, deletion, and updating of value. What is Collision? Collision in Hashing occurs when two different keys map to the same hash value. Hash collisions can be intentionally created for many hash algorithms. The probability of a hash collision depends on the size of the ...
In this study aimed at solving the Multi-agent Credit Assignment (MCA) problem, we introduce the Task Start Threshold (TST) of agents as a new constraint in a multi-score operational environment, transforming the MCA into a bankruptcy problem. ... (RevAP), is introduced. Based on this algorithm, three methods PTST, T-MAS, and T-KAg, were ...
We use mixed coding to describe the selection of hubs, assignment of nodes, and choice of transportation modes in this study and use the NSGA-II algorithm with local reinforcement to solve the problem. ... the NSGA-II algorithm with local reinforcement can significantly improve the convergence speed of the algorithm; There is benefit inversion ...