how to hypothesis test normal distribution

7.4.1 - Hypothesis Testing

Five step hypothesis testing procedure.

In the remaining lessons, we will use the following five step hypothesis testing procedure. This is slightly different from the five step procedure that we used when conducting randomization tests. 

• Check assumptions and write hypotheses.  The assumptions will vary depending on the test. In this lesson we'll be confirming that the sampling distribution is approximately normal by visually examining the randomization distribution. In later lessons you'll learn more objective assumptions. The null and alternative hypotheses will always be written in terms of population parameters; the null hypothesis will always contain the equality (i.e., \(=\)).
• Calculate the test statistic.  Here, we'll be using the formula below for the general form of the test statistic.
• Determine the p-value.  The p-value is the area under the standard normal distribution that is more extreme than the test statistic in the direction of the alternative hypothesis.
• Make a decision.  If \(p \leq \alpha\) reject the null hypothesis. If \(p>\alpha\) fail to reject the null hypothesis.
• State a "real world" conclusion.  Based on your decision in step 4, write a conclusion in terms of the original research question.

General Form of a Test Statistic

When using a standard normal distribution (i.e., z distribution), the test statistic is the standardized value that is the boundary of the p-value. Recall the formula for a z score: \(z=\frac{x-\overline x}{s}\). The formula for a test statistic will be similar. When conducting a hypothesis test the sampling distribution will be centered on the null parameter and the standard deviation is known as the standard error.

This formula puts our observed sample statistic on a standard scale (e.g., z distribution). A z score tells us where a score lies on a normal distribution in standard deviation units. The test statistic tells us where our sample statistic falls on the sampling distribution in standard error units.

7.4.1.1 - Video Example: Mean Body Temperature

Research question:  Is the mean body temperature in the population different from 98.6° Fahrenheit?

7.4.1.2 - Video Example: Correlation Between Printer Price and PPM

Research question:  Is there a positive correlation in the population between the price of an ink jet printer and how many pages per minute (ppm) it prints?

7.4.1.3 - Example: Proportion NFL Coin Toss Wins

Research question:  Is the proportion of NFL overtime coin tosses that are won different from 0.50?

StatKey was used to construct a randomization distribution:

Step 1: Check assumptions and write hypotheses

From the given StatKey output, the randomization distribution is approximately normal.

\(H_0\colon p=0.50\)

\(H_a\colon p \ne 0.50\)

Step 2: Calculate the test statistic

\(test\;statistic=\dfrac{sample\;statistic-null\;parameter}{standard\;error}\)

The sample statistic is the proportion in the original sample, 0.561. The null parameter is 0.50. And, the standard error is 0.024.

\(test\;statistic=\dfrac{0.561-0.50}{0.024}=\dfrac{0.061}{0.024}=2.542\)

Step 3: Determine the p value

The p value will be the area on the z distribution that is more extreme than the test statistic of 2.542, in the direction of the alternative hypothesis. This is a two-tailed test:

The p value is the area in the left and right tails combined: \(p=0.0055110+0.0055110=0.011022\)

Step 4: Make a decision

The p value (0.011022) is less than the standard 0.05 alpha level, therefore we reject the null hypothesis.

Step 5: State a "real world" conclusion

There is evidence that the proportion of all NFL overtime coin tosses that are won is different from 0.50

7.4.1.4 - Example: Proportion of Women Students

Research question : Are more than 50% of all World Campus STAT 200 students women?

Data were collected from a representative sample of 501 World Campus STAT 200 students. In that sample, 284 students were women and 217 were not women. 

StatKey was used to construct a sampling distribution using randomization methods:

Because this randomization distribution is approximately normal, we can find the p value by computing a standardized test statistic and using the z distribution.

The assumption here is that the sampling distribution is approximately normal. From the given StatKey output, the randomization distribution is approximately normal. 

\(H_0\colon p=0.50\) \(H_a\colon p>0.50\)

2. Calculate the test statistic

\(test\;statistic=\dfrac{sample\;statistic-hypothesized\;parameter}{standard\;error}\)

The sample statistic is \(\widehat p = 284/501 = 0.567\).

The hypothesized parameter is the value from the hypotheses: \(p_0=0.50\).

The standard error on the randomization distribution above is 0.022.

\(test\;statistic=\dfrac{0.567-0.50}{0.022}=3.045\)

3. Determine the p value

We can find the p value by constructing a standard normal distribution and finding the area under the curve that is more extreme than our observed test statistic of 3.045, in the direction of the alternative hypothesis. In other words, \(P(z>3.045)\):

Our p value is 0.0011634

4. Make a decision

Our p value is less than or equal to the standard 0.05 alpha level, therefore we reject the null hypothesis.

5. State a "real world" conclusion

There is evidence that the proportion of all World Campus STAT 200 students who are women is greater than 0.50.

7.4.1.5 - Example: Mean Quiz Score

Research question:  Is the mean quiz score different from 14 in the population?

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.2: Tests in the Normal Model

• Last updated
• Save as PDF
• Page ID 10212

• Kyle Siegrist
• University of Alabama in Huntsville via Random Services

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Basic Theory

The normal model.

The normal distribution is perhaps the most important distribution in the study of mathematical statistics, in part because of the central limit theorem. As a consequence of this theorem, a measured quantity that is subject to numerous small, random errors will have, at least approximately, a normal distribution. Such variables are ubiquitous in statistical experiments, in subjects varying from the physical and biological sciences to the social sciences.

So in this section, we assume that \(\bs{X} = (X_1, X_2, \ldots, X_n)\) is a random sample from the normal distribution with mean \(\mu\) and standard deviation \(\sigma\). Our goal in this section is to to construct hypothesis tests for \(\mu\) and \(\sigma\); these are among of the most important special cases of hypothesis testing. This section parallels the section on Estimation in the Normal Model in the chapter on Set Estimation, and in particular, the duality between interval estimation and hypothesis testing will play an important role. But first we need to review some basic facts that will be critical for our analysis.

Recall that the sample mean \( M \) and sample variance \( S^2 \) are \[ M = \frac{1}{n} \sum_{i=1}^n X_i, \quad S^2 = \frac{1}{n - 1} \sum_{i=1}^n (X_i - M)^2\]

From our study of point estimation, recall that \( M \) is an unbiased and consistent estimator of \( \mu \) while \( S^2 \) is an unbiased and consistent estimator of \( \sigma^2 \). From these basic statistics we can construct the test statistics that will be used to construct our hypothesis tests. The following results were established in the section on Special Properties of the Normal Distribution.

Define \[ Z = \frac{M - \mu}{\sigma \big/ \sqrt{n}}, \quad T = \frac{M - \mu}{S \big/ \sqrt{n}}, \quad V = \frac{n - 1}{\sigma^2} S^2 \]

• \( Z \) has the standard normal distribution.
• \( T \) has the student \( t \) distribution with \( n - 1 \) degrees of freedom.
• \( V \) has the chi-square distribution with \( n - 1 \) degrees of freedom.
• \( Z \) and \( V \) are independent.

It follows that each of these random variables is a pivot variable for \( (\mu, \sigma) \) since the distributions do not depend on the parameters, but the variables themselves functionally depend on one or both parameters. The pivot variables will lead to natural test statistics that can then be used to perform the hypothesis tests of the parameters. To construct our tests, we will need quantiles of these standard distributions. The quantiles can be computed using the special distribution calculator or from most mathematical and statistical software packages. Here is the notation we will use:

Let \( p \in (0, 1) \) and \( k \in \N_+ \).

• \( z(p) \) denotes the quantile of order \( p \) for the standard normal distribution.
• \(t_k(p)\) denotes the quantile of order \( p \) for the student \( t \) distribution with \( k \) degrees of freedom.
• \( \chi^2_k(p) \) denotes the quantile of order \( p \) for the chi-square distribution with \( k \) degrees of freedom

Since the standard normal and student \( t \) distributions are symmetric about 0, it follows that \( z(1 - p) = -z(p) \) and \( t_k(1 - p) = -t_k(p) \) for \( p \in (0, 1) \) and \( k \in \N_+ \). On the other hand, the chi-square distribution is not symmetric.

Tests for the Mean with Known Standard Deviation

For our first discussion, we assume that the distribution mean \( \mu \) is unknown but the standard deviation \( \sigma \) is known. This is not always an artificial assumption. There are often situations where \( \sigma \) is stable over time, and hence is at least approximately known, while \( \mu \) changes because of different treatments . Examples are given in the computational exercises below.

For a conjectured \( \mu_0 \in \R \), define the test statistic \[ Z = \frac{M - \mu_0}{\sigma \big/ \sqrt{n}} \]

• If \( \mu = \mu_0 \) then \( Z \) has the standard normal distribution.
• If \( \mu \ne \mu_0 \) then \( Z \) has the normal distribution with mean \( \frac{\mu - \mu_0}{\sigma / \sqrt{n}} \) and variance 1.

So in case (b), \( \frac{\mu - \mu_0}{\sigma / \sqrt{n}} \) can be viewed as a non-centrality parameter . The graph of the probability density function of \( Z \) is like that of the standard normal probability density function, but shifted to the right or left by the non-centrality parameter, depending on whether \( \mu \gt \mu_0 \) or \( \mu \lt \mu_0 \).

For \( \alpha \in (0, 1) \), each of the following tests has significance level \( \alpha \):

• Reject \( H_0: \mu = \mu_0 \) versus \( H_1: \mu \ne \mu_0 \) if and only if \( Z \lt -z(1 - \alpha /2) \) or \( Z \gt z(1 - \alpha / 2) \) if and only if \( M \lt \mu_0 - z(1 - \alpha / 2) \frac{\sigma}{\sqrt{n}} \) or \( M \gt \mu_0 + z(1 - \alpha / 2) \frac{\sigma}{\sqrt{n}} \).
• Reject \( H_0: \mu \le \mu_0 \) versus \( H_1: \mu \gt \mu_0 \) if and only if \( Z \gt z(1 - \alpha) \) if and only if \( M \gt \mu_0 + z(1 - \alpha) \frac{\sigma}{\sqrt{n}} \).
• Reject \( H_0: \mu \ge \mu_0 \) versus \( H_1: \mu \lt \mu_0 \) if and only if \( Z \lt -z(1 - \alpha) \) if and only if \( M \lt \mu_0 - z(1 - \alpha) \frac{\sigma}{\sqrt{n}} \).

In part (a), \( H_0 \) is a simple hypothesis, and under \( H_0 \), \( Z \) has the standard normal distribution. So \( \alpha \) is probability of falsely rejecting \( H_0 \) by definition of the quantiles. In parts (b) and (c), \( Z \) has a non-central normal distribution under \( H_0 \) as discussed above . So if \( H_0 \) is true, the the maximum type 1 error probability \( \alpha \) occurs when \( \mu = \mu_0 \). The decision rules in terms of \( M \) are equivalent to the corresponding ones in terms of \( Z \) by simple algebra.

Part (a) is the standard two-sided test, while (b) is the right-tailed test and (c) is the left-tailed test. Note that in each case, the hypothesis test is the dual of the corresponding interval estimate constructed in the section on Estimation in the Normal Model.

For each of the tests above , we fail to reject \(H_0\) at significance level \(\alpha\) if and only if \(\mu_0\) is in the corresponding \(1 - \alpha\) confidence interval, that is

• \( M - z(1 - \alpha / 2) \frac{\sigma}{\sqrt{n}} \le \mu_0 \le M + z(1 - \alpha / 2) \frac{\sigma}{\sqrt{n}} \)
• \( \mu_0 \le M + z(1 - \alpha) \frac{\sigma}{\sqrt{n}}\)
• \( \mu_0 \ge M - z(1 - \alpha) \frac{\sigma}{\sqrt{n}}\)

This follows from the previous result . In each case, we start with the inequality that corresponds to not rejecting \( H_0 \) and solve for \( \mu_0 \).

The two-sided test in (a) corresponds to \( \alpha / 2 \) in each tail of the distribution of the test statistic \( Z \), under \( H_0 \). This set is said to be unbiased . But of course we can construct other biased tests by partitioning the confidence level \( \alpha \) between the left and right tails in a non-symmetric way.

For every \(\alpha, \, p \in (0, 1)\), the following test has significance level \(\alpha\): Reject \(H_0: \mu = \mu_0\) versus \(H_1: \mu \ne \mu_0\) if and only if \(Z \lt z(\alpha - p \alpha)\) or \(Z \ge z(1 - p \alpha)\).

• \( p = \frac{1}{2} \) gives the symmetric, unbiased test.
• \( p \downarrow 0 \) gives the left-tailed test.
• \( p \uparrow 1 \) gives the right-tailed test.

As before \( H_0 \) is a simple hypothesis, and if \( H_0 \) is true, \( Z \) has the standard normal distribution. So the probability of falsely rejecting \( H_0 \) is \( \alpha \) by definition of the quantiles. Parts (a)–(c) follow from properties of the standard normal quantile function.

The \(P\)-value of these test can be computed in terms of the standard normal distribution function \(\Phi\).

The \(P\)-values of the standard tests above are respectively

• \( 2 \left[1 - \Phi\left(\left|Z\right|\right)\right]\)
• \( 1 - \Phi(Z) \)
• \( \Phi(Z) \)

Recall that the power function of a test of a parameter is the probability of rejecting the null hypothesis, as a function of the true value of the parameter. Our next series of results will explore the power functions of the tests above .

The power function of the general two-sided test above is given by \[ Q(\mu) = \Phi \left( z(\alpha - p \alpha) - \frac{\sqrt{n}}{\sigma} (\mu - \mu_0) \right) + \Phi \left( \frac{\sqrt{n}}{\sigma} (\mu - \mu_0) - z(1 - p \alpha) \right), \quad \mu \in \R \]

• \(Q\) is decreasing on \((-\infty, m_0)\) and increasing on \((m_0, \infty)\) where \(m_0 = \mu_0 + \left[z(\alpha - p \alpha) + z(1 - p \alpha)\right] \frac{\sqrt{n}}{2 \sigma}\).
• \(Q(\mu_0) = \alpha\).
• \(Q(\mu) \to 1\) as \(\mu \uparrow \infty\) and \(Q(\mu) \to 1\) as \(\mu \downarrow -\infty\).
• If \(p = \frac{1}{2}\) then \(Q\) is symmetric about \(\mu_0\) (and \( m_0 = \mu_0 \)).
• As \(p\) increases, \(Q(\mu)\) increases if \(\mu \gt \mu_0\) and decreases if \(\mu \lt \mu_0\).

So by varying \( p \), we can make the test more powerful for some values of \( \mu \), but only at the expense of making the test less powerful for other values of \( \mu \).

The power function of the left-tailed test above is given by

• \(Q\) is increasing on \(\R\).
• \(Q(\mu) \to 1\) as \(\mu \uparrow \infty\) and \(Q(\mu) \to 0\) as \(\mu \downarrow -\infty\).

The power function of the right-tailed test above , is given by \[ Q(\mu) = \Phi \left( z(\alpha) - \frac{\sqrt{n}}{\sigma}(\mu - \mu_0) \right), \quad \mu \in \R \]

• \(Q\) is decreasing on \(\R\).
• \(Q(\mu) \to 0\) as \(\mu \uparrow \infty\) and \(Q(\mu) \to 1\) as \(\mu \downarrow -\infty\).

For any of the three tests in above , increasing the sample size \(n\) or decreasing the standard deviation \(\sigma\) results in a uniformly more powerful test.

In the mean test experiment, select the normal test statistic and select the normal sampling distribution with standard deviation \(\sigma = 2\), significance level \(\alpha = 0.1\), sample size \(n = 20\), and \(\mu_0 = 0\). Run the experiment 1000 times for several values of the true distribution mean \(\mu\). For each value of \(\mu\), note the relative frequency of the event that the null hypothesis is rejected. Sketch the empirical power function.

In the mean estimate experiment, select the normal pivot variable and select the normal distribution with \(\mu = 0\) and standard deviation \(\sigma = 2\), confidence level \(1 - \alpha = 0.90\), and sample size \(n = 10\). For each of the three types of confidence intervals, run the experiment 20 times. State the corresponding hypotheses and significance level, and for each run, give the set of \(\mu_0\) for which the null hypothesis would be rejected.

In many cases, the first step is to design the experiment so that the significance level is \(\alpha\) and so that the test has a given power \(\beta\) for a given alternative \(\mu_1\).

For either of the one-sided tests in above , the sample size \(n\) needed for a test with significance level \(\alpha\) and power \(\beta\) for the alternative \(\mu_1\) is \[ n = \left( \frac{\sigma \left[z(\beta) - z(\alpha)\right]}{\mu_1 - \mu_0} \right)^2 \]

This follows from setting the power function equal to \(\beta\) and solving for \(n\)

For the unbiased, two-sided test, the sample size \(n\) needed for a test with significance level \(\alpha\) and power \(\beta\) for the alternative \(\mu_1\) is approximately \[ n = \left( \frac{\sigma \left[z(\beta) - z(\alpha / 2)\right]}{\mu_1 - \mu_0} \right)^2 \]

In the power function for the two-sided test given above , we can neglect the first term if \(\mu_1 \lt \mu_0\) and neglect the second term if \(\mu_1 \gt \mu_0\).

Tests of the Mean with Unknown Standard Deviation

For our next discussion, we construct tests of \(\mu\) without requiring the assumption that \(\sigma\) is known. And in applications of course, \( \sigma \) is usually unknown.

For a conjectured \( \mu_0 \in \R \), define the test statistic \[ T = \frac{M - \mu_0}{S \big/ \sqrt{n}} \]

• If \( \mu = \mu_0 \), the statistic \( T \) has the student \( t \) distribution with \( n - 1 \) degrees of freedom.
• If \( \mu \ne \mu_0 \) then \( T \) has a non-central \( t \) distribution with \( n - 1 \) degrees of freedom and non-centrality parameter \( \frac{\mu - \mu_0}{\sigma / \sqrt{n}} \).

In case (b), the graph of the probability density function of \( T \) is much (but not exactly) the same as that of the ordinary \( t \) distribution with \( n - 1 \) degrees of freedom, but shifted to the right or left by the non-centrality parameter, depending on whether \( \mu \gt \mu_0 \) or \( \mu \lt \mu_0 \).

• Reject \( H_0: \mu = \mu_0 \) versus \( H_1: \mu \ne \mu_0 \) if and only if \( T \lt -t_{n-1}(1 - \alpha /2) \) or \( T \gt t_{n-1}(1 - \alpha / 2) \) if and only if \( M \lt \mu_0 - t_{n-1}(1 - \alpha / 2) \frac{S}{\sqrt{n}} \) or \( T \gt \mu_0 + t_{n-1}(1 - \alpha / 2) \frac{S}{\sqrt{n}} \).
• Reject \( H_0: \mu \le \mu_0 \) versus \( H_1: \mu \gt \mu_0 \) if and only if \( T \gt t_{n-1}(1 - \alpha) \) if and only if \( M \gt \mu_0 + t_{n-1}(1 - \alpha) \frac{S}{\sqrt{n}} \).
• Reject \( H_0: \mu \ge \mu_0 \) versus \( H_1: \mu \lt \mu_0 \) if and only if \( T \lt -t_{n-1}(1 - \alpha) \) if and only if \( M \lt \mu_0 - t_{n-1}(1 - \alpha) \frac{S}{\sqrt{n}} \).

In part (a), \( T \) has the chi-square distribution with \( n - 1 \) degrees of freedom under \( H_0 \). So if \( H_0 \) is true, the probability of falsely rejecting \( H_0 \) is \( \alpha \) by definition of the quantiles. In parts (b) and (c), \( T \) has a non-central \( t \) distribution with \( n - 1 \) degrees of freedom under \( H_0 \), as discussed above . Hence if \( H_0 \) is true, the maximum type 1 error probability \( \alpha \) occurs when \( \mu = \mu_0 \). The decision rules in terms of \( M \) are equivalent to the corresponding ones in terms of \( T \) by simple algebra.

For each of the tests above , we fail to reject \(H_0\) at significance level \(\alpha\) if and only if \(\mu_0\) is in the corresponding \(1 - \alpha\) confidence interval.

• \( M - t_{n-1}(1 - \alpha / 2) \frac{S}{\sqrt{n}} \le \mu_0 \le M + t_{n-1}(1 - \alpha / 2) \frac{S}{\sqrt{n}} \)
• \( \mu_0 \le M + t_{n-1}(1 - \alpha) \frac{S}{\sqrt{n}}\)
• \( \mu_0 \ge M - t_{n-1}(1 - \alpha) \frac{S}{\sqrt{n}}\)

This follows from the previous result . In each case, we start with the inequality that corresponds to not rejecting \( H_0 \) and then solve for \( \mu_0 \).

The two-sided test in (a) corresponds to \( \alpha / 2 \) in each tail of the distribution of the test statistic \( T \), under \( H_0 \). This set is said to be unbiased . But of course we can construct other biased tests by partitioning the confidence level \( \alpha \) between the left and right tails in a non-symmetric way.

For every \(\alpha, \, p \in (0, 1)\), the following test has significance level \(\alpha\): Reject \(H_0: \mu = \mu_0\) versus \(H_1: \mu \ne \mu_0\) if and only if \(T \lt t_{n-1}(\alpha - p \alpha)\) or \(T \ge t_{n-1}(1 - p \alpha)\) if and only if \( M \lt \mu_0 + t_{n-1}(\alpha - p \alpha) \frac{S}{\sqrt{n}} \) or \( M \gt \mu_0 + t_{n-1}(1 - p \alpha) \frac{S}{\sqrt{n}} \).

Once again, \( H_0 \) is a simple hypothesis, and under \( H_0 \) the test statistic \( T \) has the student \( t \) distribution with \( n - 1 \) degrees of freedom. So if \( H_0 \) is true, the probability of falsely rejecting \( H_0 \) is \( \alpha \) by definition of the quantiles. Parts (a)–(c) follow from properties of the quantile function.

The \(P\)-value of these test can be computed in terms of the distribution function \(\Phi_{n-1}\) of the \(t\)-distribution with \(n - 1\) degrees of freedom.

• \( 2 \left[1 - \Phi_{n-1}\left(\left|T\right|\right)\right]\)
• \( 1 - \Phi_{n-1}(T) \)
• \( \Phi_{n-1}(T) \)

In the mean test experiment, select the student test statistic and select the normal sampling distribution with standard deviation \(\sigma = 2\), significance level \(\alpha = 0.1\), sample size \(n = 20\), and \(\mu_0 = 1\). Run the experiment 1000 times for several values of the true distribution mean \(\mu\). For each value of \(\mu\), note the relative frequency of the event that the null hypothesis is rejected. Sketch the empirical power function.

In the mean estimate experiment, select the student pivot variable and select the normal sampling distribution with mean 0 and standard deviation 2. Select confidence level 0.90 and sample size 10. For each of the three types of intervals, run the experiment 20 times. State the corresponding hypotheses and significance level, and for each run, give the set of \(\mu_0\) for which the null hypothesis would be rejected.

The power function for the \( t \) tests above can be computed explicitly in terms of the non-central \(t\) distribution function. Qualitatively, the graphs of the power functions are similar to the case when \(\sigma\) is known, given above two-sided , left-tailed , and right-tailed cases.

If an upper bound \(\sigma_0\) on the standard deviation \(\sigma\) is known, then conservative estimates on the sample size needed for a given confidence level and a given margin of error can be obtained using the methods for the normal pivot variable, in the two-sided and one-sided cases.

Tests of the Standard Deviation

For our next discussion, we will construct hypothesis tests for the distribution standard deviation \( \sigma \). So our assumption is that \( \sigma \) is unknown, and of course almost always, \( \mu \) would be unknown as well.

For a conjectured value \( \sigma_0 \in (0, \infty)\), define the test statistic \[ V = \frac{n - 1}{\sigma_0^2} S^2 \]

• If \( \sigma = \sigma_0 \), then \( V \) has the chi-square distribution with \( n - 1 \) degrees of freedom.
• If \( \sigma \ne \sigma_0 \) then \( V \) has the gamma distribution with shape parameter \( (n - 1) / 2 \) and scale parameter \( 2 \sigma^2 \big/ \sigma_0^2 \).

Recall that the ordinary chi-square distribution with \( n - 1 \) degrees of freedom is the gamma distribution with shape parameter \( (n - 1) / 2 \) and scale parameter \( \frac{1}{2} \). So in case (b), the ordinary chi-square distribution is scaled by \( \sigma^2 \big/ \sigma_0^2 \). In particular, the scale factor is greater than 1 if \( \sigma \gt \sigma_0 \) and less than 1 if \( \sigma \lt \sigma_0 \).

For every \(\alpha \in (0, 1)\), the following test has significance level \(\alpha\):

• Reject \(H_0: \sigma = \sigma_0\) versus \(H_1: \sigma \ne \sigma_0\) if and only if \(V \lt \chi_{n-1}^2(\alpha / 2)\) or \(V \gt \chi_{n-1}^2(1 - \alpha / 2)\) if and only if \( S^2 \lt \chi_{n-1}^2(\alpha / 2) \frac{\sigma_0^2}{n - 1} \) or \( S^2 \gt \chi_{n-1}^2(1 - \alpha / 2) \frac{\sigma_0^2}{n - 1} \)
• Reject \(H_0: \sigma \ge \sigma_0\) versus \(H_1: \sigma \lt \sigma_0\) if and only if \(V \lt \chi_{n-1}^2(\alpha)\) if and only if \( S^2 \lt \chi_{n-1}^2(\alpha) \frac{\sigma_0^2}{n - 1} \)
• Reject \(H_0: \sigma \le \sigma_0\) versus \(H_1: \sigma \gt \sigma_0\) if and only if \(V \gt \chi_{n-1}^2(1 - \alpha)\) if and only if \( S^2 \gt \chi_{n-1}^2(1 - \alpha) \frac{\sigma_0^2}{n - 1} \)

The logic is largely the same as with our other hypothesis test. In part (a), \( H_0 \) is a simple hypothesis, and under \( H_0 \), the test statistic \( V \) has the chi-square distribution with \( n - 1 \) degrees of freedom. So if \( H_0 \) is true, the probability of falsely rejecting \( H_0 \) is \( \alpha \) by definition of the quantiles. In parts (b) and (c), \( V \) has the more general gamma distribution under \( H_0 \), as discussed above . If \( H_0 \) is true, the maximum type 1 error probability is \( \alpha \) and occurs when \( \sigma = \sigma_0 \).

Part (a) is the unbiased, two-sided test that corresponds to \( \alpha / 2 \) in each tail of the chi-square distribution of the test statistic \( V \), under \( H_0 \). Part (b) is the left-tailed test and part (c) is the right-tailed test. Once again, we have a duality between the hypothesis tests and the interval estimates constructed in the section on Estimation in the Normal Model.

For each of the tests in above , we fail to reject \(H_0\) at significance level \(\alpha\) if and only if \(\sigma_0^2\) is in the corresponding \(1 - \alpha\) confidence interval. That is

• \( \frac{n - 1}{\chi_{n-1}^2(1 - \alpha / 2)} S^2 \le \sigma_0^2 \le \frac{n - 1}{\chi_{n-1}^2(\alpha / 2)} S^2 \)
• \( \sigma_0^2 \le \frac{n - 1}{\chi_{n-1}^2(\alpha)} S^2 \)
• \( \sigma_0^2 \ge \frac{n - 1}{\chi_{n-1}^2(1 - \alpha)} S^2 \)

This follows from the previous result . In each case, we start with the inequality that corresponds to not rejecting \( H_0 \) and then solve for \( \sigma_0^2 \).

As before, we can construct more general two-sided tests by partitioning the significance level \( \alpha \) between the left and right tails of the chi-square distribution in an arbitrary way.

For every \(\alpha, \, p \in (0, 1)\), the following test has significance level \(\alpha\): Reject \(H_0: \sigma = \sigma_0\) versus \(H_1: \sigma \ne \sigma_0\) if and only if \(V \le \chi_{n-1}^2(\alpha - p \alpha)\) or \(V \ge \chi_{n-1}^2(1 - p \alpha)\) if and only if \( S^2 \lt \chi_{n-1}^2(\alpha - p \alpha) \frac{\sigma_0^2}{n - 1} \) or \( S^2 \gt \chi_{n-1}^2(1 - p \alpha) \frac{\sigma_0^2}{n - 1} \).

• \( p = \frac{1}{2} \) gives the equal-tail test.
• \( p \downarrow 0 \) gives the left-tail test.
• \( p \uparrow 1 \) gives the right-tail test.

As before, \( H_0 \) is a simple hypothesis, and under \( H_0 \) the test statistic \( V \) has the chi-square distribution with \( n - 1 \) degrees of freedom. So if \( H_0 \) is true, the probability of falsely rejecting \( H_0 \) is \( \alpha \) by definition of the quantiles. Parts (a)–(c) follow from properties of the quantile function.

Recall again that the power function of a test of a parameter is the probability of rejecting the null hypothesis, as a function of the true value of the parameter. The power functions of the tests for \( \sigma \) can be expressed in terms of the distribution function \( G_{n-1} \) of the chi-square distribution with \( n - 1 \) degrees of freedom.

The power function of the general two-sided test above is given by the following formula, and satisfies the given properties: \[ Q(\sigma) = 1 - G_{n-1} \left( \frac{\sigma_0^2}{\sigma^2} \chi_{n-1}^2(1 - p \, \alpha) \right) + G_{n-1} \left(\frac{\sigma_0^2}{\sigma^2} \chi_{n-1}^2(\alpha - p \, \alpha) \right)\]

• \(Q\) is decreasing on \((-\infty, \sigma_0)\) and increasing on \((\sigma_0, \infty)\).
• \(Q(\sigma_0) = \alpha\).
• \(Q(\sigma) \to 1\) as \(\sigma \uparrow \infty\) and \(Q(\sigma) \to 1\) as \(\sigma \downarrow 0\).

The power function of the left-tailed test in above is given by the following formula, and satisfies the given properties: \[ Q(\sigma) = 1 - G_{n-1} \left( \frac{\sigma_0^2}{\sigma^2} \chi_{n-1}^2(1 - \alpha) \right) \]

• \(Q\) is increasing on \((0, \infty)\).
• \(Q(\sigma) \to 1\) as \(\sigma \uparrow \infty\) and \(Q(\sigma) \to 0\) as \(\sigma \downarrow 0\).

The power function for the right-tailed test above is given by the following formula, and satisfies the given properties: \[ Q(\sigma) = G_{n-1} \left( \frac{\sigma_0^2}{\sigma^2} \chi_{n-1}^2(\alpha) \right) \]

• \(Q\) is decreasing on \((0, \infty)\).
• \(Q(\sigma_0) =\alpha\).
• \(Q(\sigma) \to 0\) as \(\sigma \uparrow \infty)\) and \(Q(\sigma) \to 0\) as \(\sigma \uparrow \infty\) and as \(\sigma \downarrow 0\).

In the variance test experiment, select the normal distribution with mean 0, and select significance level 0.1, sample size 10, and test standard deviation 1.0. For various values of the true standard deviation, run the simulation 1000 times. Record the relative frequency of rejecting the null hypothesis and plot the empirical power curve.

• Two-sided test
• Left-tailed test
• Right-tailed test

In the variance estimate experiment, select the normal distribution with mean 0 and standard deviation 2, and select confidence level 0.90 and sample size 10. Run the experiment 20 times. State the corresponding hypotheses and significance level, and for each run, give the set of test standard deviations for which the null hypothesis would be rejected.

• Two-sided confidence interval
• Confidence lower bound
• Confidence upper bound

The primary assumption that we made is that the underlying sampling distribution is normal. Of course, in real statistical problems, we are unlikely to know much about the sampling distribution, let alone whether or not it is normal. Suppose in fact that the underlying distribution is not normal. When the sample size \(n\) is relatively large, the distribution of the sample mean will still be approximately normal by the central limit theorem, and thus our tests of the mean \(\mu\) should still be approximately valid. On the other hand, tests of the variance \(\sigma^2\) are less robust to deviations form the assumption of normality. The following exercises explore these ideas.

In the mean test experiment, select the gamma distribution with shape parameter 1 and scale parameter 1. For the three different tests and for various significance levels, sample sizes, and values of \(\mu_0\), run the experiment 1000 times. For each configuration, note the relative frequency of rejecting \(H_0\). When \(H_0\) is true, compare the relative frequency with the significance level.

In the mean test experiment, select the uniform distribution on \([0, 4]\). For the three different tests and for various significance levels, sample sizes, and values of \(\mu_0\), run the experiment 1000 times. For each configuration, note the relative frequency of rejecting \(H_0\). When \(H_0\) is true, compare the relative frequency with the significance level.

How large \(n\) needs to be for the testing procedure to work well depends, of course, on the underlying distribution; the more this distribution deviates from normality, the larger \(n\) must be. Fortunately, convergence to normality in the central limit theorem is rapid and hence, as you observed in the exercises, we can get away with relatively small sample sizes (30 or more) in most cases.

In the variance test experiment, select the gamma distribution with shape parameter 1 and scale parameter 1. For the three different tests and for various significance levels, sample sizes, and values of \(\sigma_0\), run the experiment 1000 times. For each configuration, note the relative frequency of rejecting \(H_0\). When \(H_0\) is true, compare the relative frequency with the significance level.

In the variance test experiment, select the uniform distribution on \([0, 4]\). For the three different tests and for various significance levels, sample sizes, and values of \(\mu_0\), run the experiment 1000 times. For each configuration, note the relative frequency of rejecting \(H_0\). When \(H_0\) is true, compare the relative frequency with the significance level.

Computational Exercises

The length of a certain machined part is supposed to be 10 centimeters. In fact, due to imperfections in the manufacturing process, the actual length is a random variable. The standard deviation is due to inherent factors in the process, which remain fairly stable over time. From historical data, the standard deviation is known with a high degree of accuracy to be 0.3. The mean, on the other hand, may be set by adjusting various parameters in the process and hence may change to an unknown value fairly frequently. We are interested in testing \(H_0: \mu = 10\) versus \(H_1: \mu \ne 10\).

• Suppose that a sample of 100 parts has mean 10.1. Perform the test at the 0.1 level of significance.
• Compute the \(P\)-value for the data in (a).
• Compute the power of the test in (a) at \(\mu = 10.05\).
• Compute the approximate sample size needed for significance level 0.1 and power 0.8 when \(\mu = 10.05\).
• Test statistic 3.33, critical values \(\pm 1.645\). Reject \(H_0\).
• \(P = 0.0010\)
• The power of the test at 10.05 is approximately 0.0509.
• Sample size 223

A bag of potato chips of a certain brand has an advertised weight of 250 grams. Actually, the weight (in grams) is a random variable. Suppose that a sample of 75 bags has mean 248 and standard deviation 5. At the 0.05 significance level, perform the following tests:

• \(H_0: \mu \ge 250\) versus \(H_1: \mu \lt 250\)
• \(H_0: \sigma \ge 7\) versus \(H_1: \sigma \lt 7\)
• Test statistic \(-3.464\), critical value \(-1.665\). Reject \(H_0\).
• \(P \lt 0.0001\) so reject \(H_0\).

At a telemarketing firm, the length of a telephone solicitation (in seconds) is a random variable. A sample of 50 calls has mean 310 and standard deviation 25. At the 0.1 level of significance, can we conclude that

• \(\mu \gt 300\)?
• \(\sigma \gt 20\)?
• Test statistic 2.828, critical value 1.2988. Reject \(H_0\).
• \(P = 0.0071\) so reject \(H_0\).

At a certain farm the weight of a peach (in ounces) at harvest time is a random variable. A sample of 100 peaches has mean 8.2 and standard deviation 1.0. At the 0.01 level of significance, can we conclude that

• \(\mu \gt 8\)?
• \(\sigma \lt 1.5\)?
• Test statistic 2.0, critical value 2.363. Fail to reject \(H_0\).

The hourly wage for a certain type of construction work is a random variable with standard deviation 1.25. For sample of 25 workers, the mean wage was $6.75. At the 0.01 level of significance, can we conclude that \(\mu \lt 7.00\)?

Test statistic \(-1\), critical value \(-2.328\). Fail to reject \(H_0\).

Data Analysis Exercises

Using Michelson's data, test to see if the velocity of light is greater than 730 (+299000) km/sec, at the 0.005 significance level.

Test statistic 15.49, critical value 2.6270. Reject \(H_0\).

Using Cavendish's data, test to see if the density of the earth is less than 5.5 times the density of water, at the 0.05 significance level .

Test statistic \(-1.269\), critical value \(-1.7017\). Fail to reject \(H_0\).

Using Short's data, test to see if the parallax of the sun differs from 9 seconds of a degree, at the 0.1 significance level.

Test statistic \(-3.730\), critical value \(\pm 1.6749\). Reject \(H_0\).

Using Fisher's iris data, perform the following tests, at the 0.1 level:

• The mean petal length of Setosa irises differs from 15 mm.
• The mean petal length of Verginica irises is greater than 52 mm.
• The mean petal length of Versicolor irises is less than 44 mm.
• Test statistic \(-1.563\), critical values \(\pm 1.672\). Fail to reject \(H_0\).
• Test statistic 4.556, critical value 1.2988. Reject \(H_0\).
• Test statistic \(-1.028\), critical value \(-1.2988\). Fail to Reject \(H_0\).

• The Open University
• Guest user / Sign out
• Study with The Open University

My OpenLearn Profile

Personalise your OpenLearn profile, save your favourite content and get recognition for your learning

About this free course

Become an ou student, download this course, share this free course.

Start this free course now. Just create an account and sign in. Enrol and complete the course for a free statement of participation or digital badge if available.

4.1 The normal distribution

Here, you will look at the concept of normal distribution and the bell-shaped curve. The peak point (the top of the bell) represents the most probable occurrences, while other possible occurrences are distributed symmetrically around the peak point, creating a downward-sloping curve on either side of the peak point.

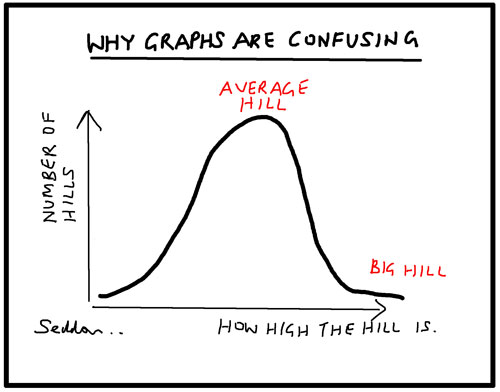
The cartoon shows a bell-shaped curve. The x-axis is titled ‘How high the hill is’ and the y-axis is titled ‘Number of hills’. The top of the bell-shaped curve is labelled ‘Average hill’, but on the lower right tail of the bell-shaped curve is labelled ‘Big hill’.

In order to test hypotheses, you need to calculate the test statistic and compare it with the value in the bell curve. This will be done by using the concept of ‘normal distribution’.

A normal distribution is a probability distribution that is symmetric about the mean, indicating that data near the mean are more likely to occur than data far from it. In graph form, a normal distribution appears as a bell curve. The values in the x-axis of the normal distribution graph represent the z-scores. The test statistic that you wish to use to test the set of hypotheses is the z-score . A z-score is used to measure how far the observation (sample mean) is from the 0 value of the bell curve (population mean). In statistics, this distance is measured by standard deviation. Therefore, when the z-score is equal to 2, the observation is 2 standard deviations away from the value 0 in the normal distribution curve.

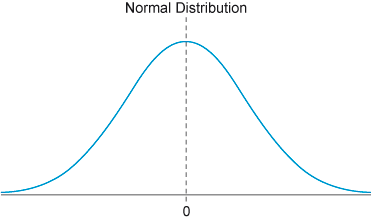
A symmetrical graph reminiscent of a bell. The top of the bell-shaped curve appears where the x-axis is at 0. This is labelled as Normal distribution.

Video Crash Courses

Junior Math

Math Essentials

Tutor-on-Demand

Encyclopedia

Digital Tools

How to Do Hypothesis Testing with Normal Distribution

Hypothesis tests compare a result against something you already believe is true. Let X 1 , X 2 , … ⁡ , X n be n independent random variables with equal expected value   μ and standard deviation  σ . Let X be the mean of these n random variables, so

The stochastic variable  X has an expected value  μ and a standard deviation  σ n . You want to perform a hypothesis test on this expected value. You have a null hypothesis  H 0 : μ = μ 0 and three possible alternative hypotheses: H a : μ < μ 0 , H a : μ > μ 0 or H a : μ ≠ μ 0 . The first two alternative hypotheses belong to what you call a one-sided test, while the latter is two-sided.

In hypothesis testing, you calculate using the alternative hypothesis in order to say something about the null hypothesis.

Hypothesis Testing (Normal Distribution)

Note! For two-sided testing, multiply the p -value by 2 before checking against the critical region.

As the production manager at the new soft drink factory, you are worried that the machines don’t fill the bottles to their proper capacity. Each bottle should be filled with 0 . 5 L soda, but random samples show that 48 soda bottles have an average of 0 . 4 8 L , with an empirical standard deviation of 0 . 1 . You are wondering if you need to recalibrate the machines so that they become more precise.

This is a classic case of hypothesis testing by normal distribution. You now follow the instructions above and select 1 0 % level of significance, since it is only a quantity of soda and not a case of life and death.

The alternative hypothesis in this case is that the bottles do not contain 0 . 5 L and that the machines are not precise enough. This thus becomes a two-sided hypothesis test and you must therefore remember to multiply the p -value by 2 before deciding whether the p -value is in the critical region. This is because the normal distribution is symmetric, so P ( X ≥ k ) = P ( X ≤ − k ) . Thus it is just as likely to observe an equally extremely high value as an equally extreme low:

so H 0 must be kept, and the machines are deemed to be fine as is.

Had the p -value been less than the level of significance, that would have meant that the calibration represented by the alternative hypothesis would be significantly better for the business.

Teach yourself statistics

How to Test for Normality: Three Simple Tests

Many statistical techniques (regression, ANOVA, t-tests, etc.) rely on the assumption that data is normally distributed. For these techniques, it is good practice to examine the data to confirm that the assumption of normality is tenable.

With that in mind, here are three simple ways to test interval-scale data or ratio-scale data for normality.

• Check descriptive statistics.
• Generate a histogram.
• Conduct a chi-square test.

Each option is easy to implement with Excel, as long as you have Excel's Analysis ToolPak.

The Analysis ToolPak

To conduct the tests for normality described below, you need a free Microsoft add-in called the Analysis ToolPak, which may or may not be already installed on your copy of Excel.

To determine whether you have the Analysis ToolPak, click the Data tab in the main Excel menu. If you see Data Analysis in the Analysis section, you're good. You have the ToolPak.

If you don't have the ToolPak, you need to get it. Go to: How to Install the Data Analysis ToolPak in Excel .

Descriptive Statistics

Perhaps, the easiest way to test for normality is to examine several common descriptive statistics. Here's what to look for:

• Central tendency. The mean and the median are summary measures used to describe central tendency - the most "typical" value in a set of values. With a normal distribution, the mean is equal to the median.
• Skewness. Skewness is a measure of the asymmetry of a probability distribution. If observations are equally distributed around the mean, the skewness value is zero; otherwise, the skewness value is positive or negative. As a rule of thumb, skewness between -2 and +2 is consistent with a normal distribution.
• Kurtosis. Kurtosis is a measure of whether observations cluster around the mean of the distribution or in the tails of the distribution. The normal distribution has a kurtosis value of zero. As a rule of thumb, kurtosis between -2 and +2 is consistent with a normal distribution.

Together, these descriptive measures provide a useful basis for judging whether a data set satisfies the assumption of normality.

To see how to compute descriptive statistics in Excel, consider the following data set:

Begin by entering data in a column or row of an Excel spreadsheet:

Next, from the navigation menu in Excel, click Data / Data analysis . That displays the Data Analysis dialog box. From the Data Analysis dialog box, select Descriptive Statistics and click the OK button:

Then, in the Descriptive Statistics dialog box, enter the input range, and click the Summary Statistics check box. The dialog box, with entries, should look like this:

And finally, to display summary statistics, click the OK button on the Descriptive Statistics dialog box. Among other outputs, you should see the following:

The mean is nearly equal to the median. And both skewness and kurtosis are between -2 and +2.

Conclusion: These descriptive statistics are consistent with a normal distribution.

Another easy way to test for normality is to plot data in a histogram , and see if the histogram reveals the bell-shaped pattern characteristic of a normal distribution. With Excel, this is a a four-step process:

• Enter data. This means entering data values in an Excel spreadsheet. The column, row, or range of cells that holds data is the input range .
• Define bins. In Excel, bins are category ranges. To define a bin, you enter the upper range of each bin in a column, row, or range of cells. The block of cells that holds upper-range entries is called the bin range .
• Plot the data in a histogram. In Excel, access the histogram function through: Data / Data analysis / Histogram .
• In the Histogram dialog box, enter the input range and the bin range ; and check the Chart Output box. Then, click OK.

If the resulting histogram looks like a bell-shaped curve, your work is done. The data set is normal or nearly normal. If the curve is not bell-shaped, the data may not be normal.

To see how to plot data for normality with a histogram in Excel, we'll use the same data set (shown below) that we used in Example 1.

Begin by entering data to define an input range and a bin range. Here is what data entry looks like in an Excel spreadsheet:

Next, from the navigation menu in Excel, click Data / Data analysis . That displays the Data Analysis dialog box. From the Data Analysis dialog box, select Histogram and click the OK button:

Then, in the Histogram dialog box, enter the input range, enter the bin range, and click the Chart Output check box. The dialog box, with entries, should look like this:

And finally, to display the histogram, click the OK button on the Histogram dialog box. Here is what you should see:

The plot is fairly bell-shaped - an almost-symmetric pattern with one peak in the middle. Given this result, it would be safe to assume that the data were drawn from a normal distribution. On the other hand, if the plot were not bell-shaped, you might suspect the data were not from a normal distribution.

Chi-Square Test

The chi-square test for normality is another good option for determining whether a set of data was sampled from a normal distribution.

Note: All chi-square tests assume that the data under investigation was sampled randomly.

Hypothesis Testing

The chi-square test for normality is an actual hypothesis test , where we examine observed data to choose between two statistical hypotheses:

• Null hypothesis: Data is sampled from a normal distribution.
• Alternative hypothesis: Data is not sampled from a normal distribution.

Like many other techniques for testing hypotheses, the chi-square test for normality involves computing a test-statistic and finding the P-value for the test statistic, given degrees of freedom and significance level . If the P-value is bigger than the significance level, we accept the null hypothesis; if it is smaller, we reject the null hypothesis.

How to Conduct the Chi-Square Test

The steps required to conduct a chi-square test of normality are listed below:

• Specify the significance level.
• Find the mean, standard deviation, sample size for the sample.
• Define non-overlapping bins.
• Count observations in each bin, based on actual dependent variable scores.
• Find the cumulative probability for each bin endpoint.
• Find the probability that an observation would land in each bin, assuming a normal distribution.
• Find the expected number of observations in each bin, assuming a normal distribution.
• Compute a chi-square statistic.
• Find the degrees of freedom, based on the number of bins.
• Find the P-value for the chi-square statistic, based on degrees of freedom.
• Accept or reject the null hypothesis, based on P-value and significance level.

So you will understand how to accomplish each step, let's work through an example, one step at a time.

To demonstrate how to conduct a chi-square test for normality in Excel, we'll use the same data set (shown below) that we've used for the previous two examples. Here it is again:

Now, using this data, let's check for normality.

Specify Significance Level

The significance level is the probability of rejecting the null hypothesis when it is true. Researchers often choose 0.05 or 0.01 for a significance level. For the purpose of this exercise, let's choose 0.05.

Find the Mean, Standard Deviation, and Sample Size

To compute a chi-square test statistic, we need to know the mean, standared deviation, and sample size. Excel can provide this information. Here's how:

Define Bins

To conduct a chi-square analysis, we need to define bins, based on dependent variable scores. Each bin is defined by a non-overlapping range of values.

For the chi-square test to be valid, each bin should hold at least five observations. With that in mind, we'll define four bins for this example, as shown below:

Bin 1 will hold dependent variable scores that are less than 4; Bin 2, scores between 4 and 5; Bin 3, scores between 5.1 and 6; and and Bin 4, scores greater than 6.

Note: The number of bins is an arbitrary decision made by the experimenter, as long as the experimenter chooses at least four bins and at least five observations per bin. With fewer than four bins, there are not enough degrees of freedom for the analysis. For this example, we chose to define only four bins. Given the small sample, if we used more bins, at least one bin would have fewer than five observations per bin.

Count Observed Data Points in Each Bin

The next step is to count the observed data points in each bin. The figure below shows sample observations allocated to bins, with a frequency count for each bin in the final row.

Note: We have five observed data points in each bin - the minimum required for a valid chi-square test of normality.

Find Cumulative Probability

A cumulative probability refers to the probability that a random variable is less than or equal to a specific value. In Excel, the NORMDIST function computes cumulative probabilities from a normal distribution.

Assuming our data follows a normal distribution, we can use the NORMDIST function to find cumulative probabilities for the upper endpoints in each bin. Here is the formula we use:

P j = NORMDIST (MAX j , X , s, TRUE)

where P j is the cumulative probability for the upper endpoint in Bin j , MAX j is the upper endpoint for Bin j , X is the mean of the data set, and s is the standard deviation of the data set.

When we execute the formula in Excel, we get the following results:

P 1 = NORMDIST (4, 5.1, 2.0, TRUE) = 0.29

P 2 = NORMDIST (5, 5.1, 2.0, TRUE) = 0.48

P 3 = NORMDIST (6, 5.1, 2.0, TRUE) = 0.67

P 4 = NORMDIST (999999999, 5.1, 2.0, TRUE) = 1.00

Note: For Bin 4, the upper endpoint is positive infinity (∞), a quantity that is too large to be represented in an Excel function. To estimate cumulative probability for Bin 4 (P 4 ) with excel, you can use a very large number (e.g., 999999999) in place of positive infinity (as shown above). Or you can recognize that the probability that any random variable is less than or equal to positive infinity is 1.00.

Find Bin Probability

Given the cumulative probabilities shown above, it is possible to find the probability that a randomly selected observation would fall in each bin, using the following formulas:

P( Bin = 1 ) = P 1 = 0.29

P( Bin = 2 ) = P 2 - P 1 = 0.48 - 0.29 = 0.19

P( Bin = 3 ) = P 3 - P 2 = 0.67 - 0.48 = 0.19

P( Bin = 4 ) = P 4 - P 3 = 1.000 - 0.67 = 0.33

Find Expected Number of Observations

Assuming a normal distribution, the expected number of observations in each bin can be found by using the following formula:

Exp j = P( Bin = j ) * n

where Exp j is the expected number of observations in Bin j , P( Bin = j ) is the probability that a randomly selected observation would fall in Bin j , and n is the sample size

Applying the above formula to each bin, we get the following:

Exp 1 = P( Bin = 1 ) * 20 = 0.29 * 20 = 5.8

Exp 2 = P( Bin = 2 ) * 20 = 0.19 * 20 = 3.8

Exp 3 = P( Bin = 3 ) * 20 = 0.19 * 20 = 3.8

Exp 3 = P( Bin = 4 ) * 20 = 0.33 * 20 = 6.6

Compute Chi-Square Statistic

Finally, we can compute the chi-square statistic ( χ 2 ), using the following formula:

χ 2 = Σ [ ( Obs j - Exp j ) 2 / Exp j ]

where Obs j is the observed number of observations in Bin j , and Exp j is the expected number of observations in Bin j .

Find Degrees of Freedom

Assuming a normal distribution, the degrees of freedom (df) for a chi-square test of normality equals the number of bins (n b ) minus the number of estimated parameters (n p ) minus one. We used four bins, so n b equals four. And to conduct this analysis, we estimated two parameters (the mean and the standard deviation), so n p equals two. Therefore,

df = n b - n p - 1 = 4 - 2 - 1 = 1

Find P-Value

The P-value is the probability of seeing a chi-square test statistic that is more extreme (bigger) than the observed chi-square statistic. For this problem, we found that the observed chi-square statistic was 1.26. Therefore, we want to know the probability of seeing a chi-square test statistic bigger than 1.26, given one degree of freedom.

Use Stat Trek's Chi-Square Calculator to find that probability. Enter the degrees of freedom (1) and the observed chi-square statistic (1.26) into the calculator; then, click the Calculate button.

From the calculator, we see that P( X 2 > 1.26 ) equals 0.26.

Test Null Hypothesis

When the P-Value is bigger than the significance level, we cannot reject the null hypothesis. Here, the P-Value (0.26) is bigger than the significance level (0.05), so we cannot reject the null hypothesis that the data tested follows a normal distribution.

9.3 Distribution Needed for Hypothesis Testing

Earlier in the course, we discussed sampling distributions. Particular distributions are associated with hypothesis testing. Perform tests of a population mean using a normal distribution or a Student's t -distribution . (Remember, use a Student's t -distribution when the population standard deviation is unknown and the distribution of the sample mean is approximately normal.) We perform tests of a population proportion using a normal distribution (usually n is large).

Assumptions

When you perform a hypothesis test of a single population mean μ using a Student's t -distribution (often called a t -test), there are fundamental assumptions that need to be met in order for the test to work properly. Your data should be a simple random sample that comes from a population that is approximately normally distributed . You use the sample standard deviation to approximate the population standard deviation. Note that if the sample size is sufficiently large, a t -test will work even if the population is not approximately normally distributed.

When you perform a hypothesis test of a single population mean μ using a normal distribution (often called a z -test), you take a simple random sample from the population. The population you are testing is normally distributed or your sample size is sufficiently large. You know the value of the population standard deviation which, in reality, is rarely known.

When you perform a hypothesis test of a single population proportion p , you take a simple random sample from the population. You must meet the conditions for a binomial distribution , which are the following: there are a certain number n of independent trials, the outcomes of any trial are success or failure, and each trial has the same probability of a success p . The shape of the binomial distribution needs to be similar to the shape of the normal distribution. To ensure this, the quantities np and nq must both be greater than five ( np > 5 and nq > 5). Then the binomial distribution of a sample (estimated) proportion can be approximated by the normal distribution with μ = p and σ = p q n σ = p q n . Remember that q = 1 – p .

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/statistics/pages/1-introduction

• Authors: Barbara Illowsky, Susan Dean
• Publisher/website: OpenStax
• Book title: Statistics
• Publication date: Mar 27, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/statistics/pages/1-introduction
• Section URL: https://openstax.org/books/statistics/pages/9-3-distribution-needed-for-hypothesis-testing

© Jan 23, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Module 9: Hypothesis Testing With One Sample

Distribution needed for hypothesis testing, learning outcomes.

• Conduct and interpret hypothesis tests for a single population mean, population standard deviation known
• Conduct and interpret hypothesis tests for a single population mean, population standard deviation unknown

Earlier in the course, we discussed sampling distributions.  Particular distributions are associated with hypothesis testing. Perform tests of a population mean using a normal distribution or a Student’s t- distribution . (Remember, use a Student’s t -distribution when the population standard deviation is unknown and the distribution of the sample mean is approximately normal.) We perform tests of a population proportion using a normal distribution (usually n is large or the sample size is large).

If you are testing a  single population mean , the distribution for the test is for means :

[latex]\displaystyle\overline{{X}}\text{~}{N}{\left(\mu_{{X}}\text{ , }\frac{{\sigma_{{X}}}}{\sqrt{{n}}}\right)}{\quad\text{or}\quad}{t}_{{{d}{f}}}[/latex]

The population parameter is [latex]\mu[/latex]. The estimated value (point estimate) for [latex]\mu[/latex] is [latex]\displaystyle\overline{{x}}[/latex], the sample mean.

If you are testing a  single population proportion , the distribution for the test is for proportions or percentages:

[latex]\displaystyle{P}^{\prime}\text{~}{N}{\left({p}\text{ , }\sqrt{{\frac{{{p}{q}}}{{n}}}}\right)}[/latex]

The population parameter is [latex]p[/latex]. The estimated value (point estimate) for [latex]p[/latex] is p′ . [latex]\displaystyle{p}\prime=\frac{{x}}{{n}}[/latex] where [latex]x[/latex] is the number of successes and [latex]n[/latex] is the sample size.

Assumptions

When you perform a  hypothesis test of a single population mean μ using a Student’s t -distribution (often called a t-test), there are fundamental assumptions that need to be met in order for the test to work properly. Your data should be a simple random sample that comes from a population that is approximately normally distributed . You use the sample standard deviation to approximate the population standard deviation. (Note that if the sample size is sufficiently large, a t-test will work even if the population is not approximately normally distributed).

When you perform a  hypothesis test of a single population mean μ using a normal distribution (often called a z -test), you take a simple random sample from the population. The population you are testing is normally distributed or your sample size is sufficiently large. You know the value of the population standard deviation which, in reality, is rarely known.

When you perform a  hypothesis test of a single population proportion p , you take a simple random sample from the population. You must meet the conditions for a binomial distribution which are as follows: there are a certain number n of independent trials, the outcomes of any trial are success or failure, and each trial has the same probability of a success p . The shape of the binomial distribution needs to be similar to the shape of the normal distribution. To ensure this, the quantities np  and nq must both be greater than five ( np > 5 and nq > 5). Then the binomial distribution of a sample (estimated) proportion can be approximated by the normal distribution with μ = p and [latex]\displaystyle\sigma=\sqrt{{\frac{{{p}{q}}}{{n}}}}[/latex] . Remember that q = 1 – p .

Concept Review

In order for a hypothesis test’s results to be generalized to a population, certain requirements must be satisfied.

When testing for a single population mean:

• A Student’s t -test should be used if the data come from a simple, random sample and the population is approximately normally distributed, or the sample size is large, with an unknown standard deviation.
• The normal test will work if the data come from a simple, random sample and the population is approximately normally distributed, or the sample size is large, with a known standard deviation.

When testing a single population proportion use a normal test for a single population proportion if the data comes from a simple, random sample, fill the requirements for a binomial distribution, and the mean number of success and the mean number of failures satisfy the conditions:  np > 5 and nq > n where n is the sample size, p is the probability of a success, and q is the probability of a failure.

Formula Review

If there is no given preconceived  α , then use α = 0.05.

Types of Hypothesis Tests

• Single population mean, known population variance (or standard deviation): Normal test .
• Single population mean, unknown population variance (or standard deviation): Student’s t -test .
• Single population proportion: Normal test .
• For a single population mean , we may use a normal distribution with the following mean and standard deviation. Means: [latex]\displaystyle\mu=\mu_{{\overline{{x}}}}{\quad\text{and}\quad}\sigma_{{\overline{{x}}}}=\frac{{\sigma_{{x}}}}{\sqrt{{n}}}[/latex]
• A single population proportion , we may use a normal distribution with the following mean and standard deviation. Proportions: [latex]\displaystyle\mu={p}{\quad\text{and}\quad}\sigma=\sqrt{{\frac{{{p}{q}}}{{n}}}}[/latex].
• Distribution Needed for Hypothesis Testing. Provided by : OpenStax. Located at : . License : CC BY: Attribution
• Introductory Statistics . Authored by : Barbara Illowski, Susan Dean. Provided by : Open Stax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]

Hypothesis Testing with the Normal Distribution

Contents Toggle Main Menu 1 Introduction 2 Test for Population Mean 3 Worked Example 3.1 Video Example 4 Approximation to the Binomial Distribution 5 Worked Example 6 Comparing Two Means 7 Workbooks 8 See Also

Introduction

When constructing a confidence interval with the standard normal distribution, these are the most important values that will be needed.

Distribution of Sample Means

where $\mu$ is the true mean and $\mu_0$ is the current accepted population mean. Draw samples of size $n$ from the population. When $n$ is large enough and the null hypothesis is true the sample means often follow a normal distribution with mean $\mu_0$ and standard deviation $\frac{\sigma}{\sqrt{n}}$. This is called the distribution of sample means and can be denoted by $\bar{X} \sim \mathrm{N}\left(\mu_0, \frac{\sigma}{\sqrt{n}}\right)$. This follows from the central limit theorem .

The $z$-score will this time be obtained with the formula \[Z = \dfrac{\bar{X} - \mu_0}{\frac{\sigma}{\sqrt{n}}}.\]

So if $\mu = \mu_0, X \sim \mathrm{N}\left(\mu_0, \frac{\sigma}{\sqrt{n}}\right)$ and $ Z \sim \mathrm{N}(0,1)$.

The alternative hypothesis will then take one of the following forms: depending on what we are testing.

Worked Example

An automobile company is looking for fuel additives that might increase gas mileage. Without additives, their cars are known to average $25$ mpg (miles per gallons) with a standard deviation of $2.4$ mpg on a road trip from London to Edinburgh. The company now asks whether a particular new additive increases this value. In a study, thirty cars are sent on a road trip from London to Edinburgh. Suppose it turns out that the thirty cars averaged $\overline{x}=25.5$ mpg with the additive. Can we conclude from this result that the additive is effective?

We are asked to show if the new additive increases the mean miles per gallon. The current mean $\mu = 25$ so the null hypothesis will be that nothing changes. The alternative hypothesis will be that $\mu > 25$ because this is what we have been asked to test.

\begin{align} &H_0:\mu=25. \\ &H_1:\mu>25. \end{align}

Now we need to calculate the test statistic. We start with the assumption the normal distribution is still valid. This is because the null hypothesis states there is no change in $\mu$. Thus, as the value $\sigma=2.4$ mpg is known, we perform a hypothesis test with the standard normal distribution. So the test statistic will be a $z$ score. We compute the $z$ score using the formula \[z=\frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt{n} } }.\] So \begin{align} z&=\frac{\overline{x}-25}{\frac{2.4}{\sqrt{30} } }\\ &=1.14 \end{align}

We are using a $5$% significance level and a (right-sided) one-tailed test, so $\alpha=0.05$ so from the tables we obtain $z_{1-\alpha} = 1.645$ is our test statistic.

As $1.14<1.645$, the test statistic is not in the critical region so we cannot reject $H_0$. Thus, the observed sample mean $\overline{x}=25.5$ is consistent with the hypothesis $H_0:\mu=25$ on a $5$% significance level.

Video Example

In this video, Dr Lee Fawcett explains how to conduct a hypothesis test for the mean of a single distribution whose variance is known, using a one-sample z-test.

Approximation to the Binomial Distribution

A supermarket has come under scrutiny after a number of complaints that its carrier bags fall apart when the load they carry is $5$kg. Out of a random sample of $200$ bags, $185$ do not tear when carrying a load of $5$kg. Can the supermarket claim at a $5$% significance level that more that $90$% of the bags will not fall apart?

Let $X$ represent the number of carrier bags which can hold a load of $5$kg. Then $X \sim \mathrm{Bin}(200,p)$ and \begin{align}H_0&: p = 0.9 \\ H_1&: p > 0.9 \end{align}

We need to calculate the mean $\mu$ and variance $\sigma ^2$.

\[\mu = np = 200 \times 0.9 = 180\text{.}\] \[\sigma ^2= np(1-p) = 18\text{.}\]

Using the normal approximation to the binomial distribution we obtain $Y \sim \mathrm{N}(180, 18)$.

\[\mathrm{P}[X \geq 185] = \mathrm{P}\left[Z \geq \dfrac{184.5 - 180}{4.2426} \right] = \mathrm{P}\left[Z \geq 1.0607\right] \text{.}\]

Because we are using a one-tailed test at a $5$% significance level, we obtain the critical value $Z=1.645$. Now $1.0607 < 1.645$ so we cannot accept the alternative hypothesis. It is not true that over $90$% of the supermarket's carrier bags are capable of withstanding a load of $5$kg.

Comparing Two Means

When we test hypotheses with two means, we will look at the difference $\mu_1 - \mu_2$. The null hypothesis will be of the form

where $a$ is a constant. Often $a=0$ is used to test if the two means are the same. Given two continuous random variables $X_1$ and $X_2$ with means $\mu_1$ and $\mu_2$ and variances $\frac{\sigma_1^2}{n_1}$ and $\frac{\sigma_2^2}{n_2}$ respectively \[\mathrm{E} [\bar{X_1} - \bar{X_2} ] = \mathrm{E} [\bar{X_1}] - \mathrm{E} [\bar{X_2}] = \mu_1 - \mu_2\] and \[\mathrm{Var}[\bar{X_1} - \bar{X_2}] = \mathrm{Var}[\bar{X_1}] - \mathrm{Var}[\bar{X_2}]=\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}\text{.}\] Note this last result, the difference of the variances is calculated by summing the variances.

We then obtain the $z$-score using the formula \[Z = \frac{(\bar{X_1}-\bar{X_2})-(\mu_1 - \mu_2)}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}\text{.}\]

These workbooks produced by HELM are good revision aids, containing key points for revision and many worked examples.

• Tests concerning a single sample
• Tests concerning two samples

Selecting a Hypothesis Test

Statistics Made Easy

How to Test for Normality in Python (4 Methods)

Many statistical tests make the assumption that datasets are normally distributed.

There are four common ways to check this assumption in Python:

1. (Visual Method) Create a histogram.

• If the histogram is roughly “bell-shaped”, then the data is assumed to be normally distributed.

2. (Visual Method) Create a Q-Q plot.

• If the points in the plot roughly fall along a straight diagonal line, then the data is assumed to be normally distributed.

3. (Formal Statistical Test) Perform a Shapiro-Wilk Test.

• If the p-value of the test is greater than α = .05, then the data is assumed to be normally distributed.

4. (Formal Statistical Test) Perform a Kolmogorov-Smirnov Test.

The following examples show how to use each of these methods in practice.

Method 1: Create a Histogram

The following code shows how to create a histogram for a dataset that follows a log-normal distribution :

By simply looking at this histogram, we can tell the dataset does not exhibit a “bell-shape” and is not normally distributed.

Method 2: Create a Q-Q plot

The following code shows how to create a Q-Q plot for a dataset that follows a log-normal distribution:

If the points on the plot fall roughly along a straight diagonal line, then we typically assume a dataset is normally distributed.

However, the points on this plot clearly don’t fall along the red line, so we would not assume that this dataset is normally distributed.

This should make sense considering we generated the data using a log-normal distribution function.

Method 3: Perform a Shapiro-Wilk Test

The following code shows how to perform a Shapiro-Wilk for a dataset that follows a log-normal distribution:

From the output we can see that the test statistic is  0.857 and the corresponding p-value is  3.88e-29  (extremely close to zero).

Since the p-value is less than .05, we reject the null hypothesis of the Shapiro-Wilk test.

This means we have sufficient evidence to say that the sample data does not come from a normal distribution.

Method 4: Perform a Kolmogorov-Smirnov Test

The following code shows how to perform a Kolmogorov-Smirnov test for a dataset that follows a log-normal distribution:

From the output we can see that the test statistic is  0.841 and the corresponding p-value is 0.0 .

Since the p-value is less than .05, we reject the null hypothesis of the Kolmogorov-Smirnov test.

How to Handle Non-Normal Data

If a given dataset is not normally distributed, we can often perform one of the following transformations to make it more normally distributed:

1. Log Transformation:  Transform the values from x to log(x) .

2. Square Root Transformation:  Transform the values from x to √ x .

3. Cube Root Transformation:  Transform the values from x to x 1/3 .

By performing these transformations, the dataset typically becomes more normally distributed.

Read this tutorial to see how to perform these transformations in Python.

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

scipy.stats.normaltest #

Test whether a sample differs from a normal distribution.

This function tests the null hypothesis that a sample comes from a normal distribution. It is based on D’Agostino and Pearson’s [1] , [2] test that combines skew and kurtosis to produce an omnibus test of normality.

The array containing the sample to be tested.

If an int, the axis of the input along which to compute the statistic. The statistic of each axis-slice (e.g. row) of the input will appear in a corresponding element of the output. If None , the input will be raveled before computing the statistic.

Defines how to handle input NaNs.

propagate : if a NaN is present in the axis slice (e.g. row) along which the statistic is computed, the corresponding entry of the output will be NaN.

omit : NaNs will be omitted when performing the calculation. If insufficient data remains in the axis slice along which the statistic is computed, the corresponding entry of the output will be NaN.

raise : if a NaN is present, a ValueError will be raised.

If this is set to True, the axes which are reduced are left in the result as dimensions with size one. With this option, the result will broadcast correctly against the input array.

s^2 + k^2 , where s is the z-score returned by skewtest and k is the z-score returned by kurtosistest .

A 2-sided chi squared probability for the hypothesis test.

Beginning in SciPy 1.9, np.matrix inputs (not recommended for new code) are converted to np.ndarray before the calculation is performed. In this case, the output will be a scalar or np.ndarray of appropriate shape rather than a 2D np.matrix . Similarly, while masked elements of masked arrays are ignored, the output will be a scalar or np.ndarray rather than a masked array with mask=False .

D’Agostino, R. B. (1971), “An omnibus test of normality for moderate and large sample size”, Biometrika, 58, 341-348

D’Agostino, R. and Pearson, E. S. (1973), “Tests for departure from normality”, Biometrika, 60, 613-622

Shapiro, S. S., & Wilk, M. B. (1965). An analysis of variance test for normality (complete samples). Biometrika, 52(3/4), 591-611.

B. Phipson and G. K. Smyth. “Permutation P-values Should Never Be Zero: Calculating Exact P-values When Permutations Are Randomly Drawn.” Statistical Applications in Genetics and Molecular Biology 9.1 (2010).

Panagiotakos, D. B. (2008). The value of p-value in biomedical research. The open cardiovascular medicine journal, 2, 97.

Suppose we wish to infer from measurements whether the weights of adult human males in a medical study are not normally distributed [3] . The weights (lbs) are recorded in the array x below.

The normality test of [1] and [2] begins by computing a statistic based on the sample skewness and kurtosis.

(The test warns that our sample has too few observations to perform the test. We’ll return to this at the end of the example.) Because the normal distribution has zero skewness and zero (“excess” or “Fisher”) kurtosis, the value of this statistic tends to be low for samples drawn from a normal distribution.

The test is performed by comparing the observed value of the statistic against the null distribution: the distribution of statistic values derived under the null hypothesis that the weights were drawn from a normal distribution. For this normality test, the null distribution for very large samples is the chi-squared distribution with two degrees of freedom.

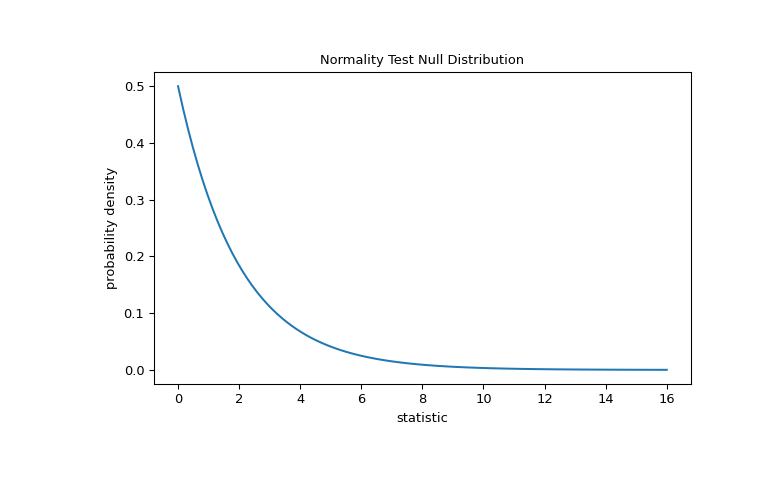
The comparison is quantified by the p-value: the proportion of values in the null distribution greater than or equal to the observed value of the statistic.

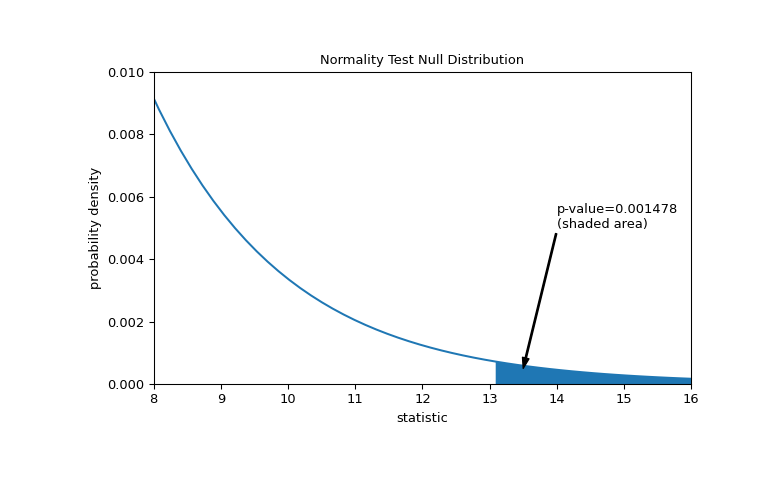
If the p-value is “small” - that is, if there is a low probability of sampling data from a normally distributed population that produces such an extreme value of the statistic - this may be taken as evidence against the null hypothesis in favor of the alternative: the weights were not drawn from a normal distribution. Note that:

The inverse is not true; that is, the test is not used to provide evidence for the null hypothesis.

The threshold for values that will be considered “small” is a choice that should be made before the data is analyzed [4] with consideration of the risks of both false positives (incorrectly rejecting the null hypothesis) and false negatives (failure to reject a false null hypothesis).

Note that the chi-squared distribution provides an asymptotic approximation of the null distribution; it is only accurate for samples with many observations. This is the reason we received a warning at the beginning of the example; our sample is quite small. In this case, scipy.stats.monte_carlo_test may provide a more accurate, albeit stochastic, approximation of the exact p-value.

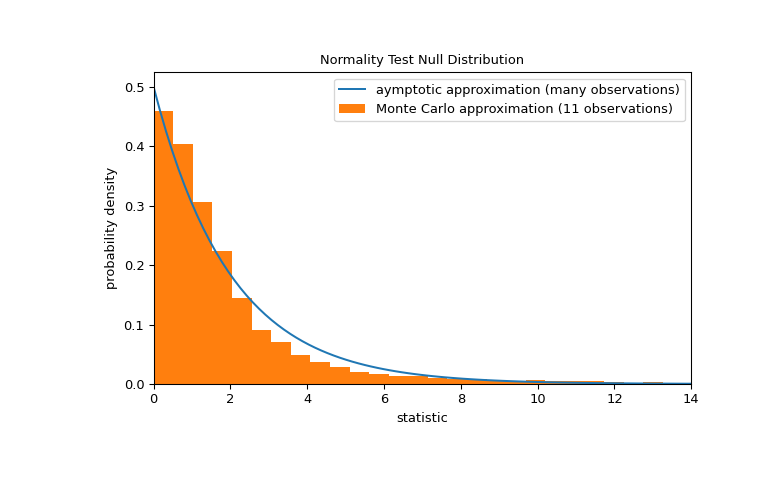
Furthermore, despite their stochastic nature, p-values computed in this way can be used to exactly control the rate of false rejections of the null hypothesis [5] .