the assignment problem can be solved by

Assignment Problem: Meaning, Methods and Variations | Operations Research

After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations.

Meaning of Assignment Problem:

An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total cost or maximize total profit of allocation.

The problem of assignment arises because available resources such as men, machines etc. have varying degrees of efficiency for performing different activities, therefore, cost, profit or loss of performing the different activities is different.

Thus, the problem is “How should the assignments be made so as to optimize the given objective”. Some of the problem where the assignment technique may be useful are assignment of workers to machines, salesman to different sales areas.

Definition of Assignment Problem:

ADVERTISEMENTS:

Suppose there are n jobs to be performed and n persons are available for doing these jobs. Assume that each person can do each job at a term, though with varying degree of efficiency, let c ij be the cost if the i-th person is assigned to the j-th job. The problem is to find an assignment (which job should be assigned to which person one on-one basis) So that the total cost of performing all jobs is minimum, problem of this kind are known as assignment problem.

The assignment problem can be stated in the form of n x n cost matrix C real members as given in the following table:

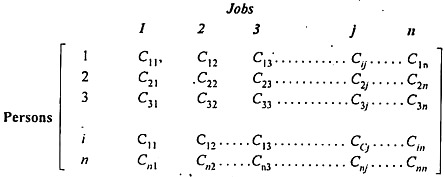
The present assignment is optimal because each row and column contain precisely one encircled zero.

Where 1 to II, 2 to IV, 3 to I, 4 to V, and 5 to III are the best assignments.

Hence, z = 15 + 14 + 21 + 20 + 16 = 86 hours is the optimal time.

Practice Question on Hungarian Method

Use the Hungarian method to solve the following assignment problem shown in table. The matrix entries represent the time it takes for each job to be processed by each machine in hours.

\(\begin{array}{l}\begin{bmatrix}J/M & I & II & III & IV & V \\1 & 9 & 22 & 58 & 11 & 19 \\2 & 43 & 78 & 72 & 50 & 63 \\3 & 41 & 28 & 91 & 37 & 45 \\4 & 74 & 42 & 27 & 49 & 39 \\5 & 36 & 11 & 57 & 22 & 25 \\\end{bmatrix}\end{array} \)

Stay tuned to BYJU’S – The Learning App and download the app to explore all Maths-related topics.

Frequently Asked Questions on Hungarian Method

What is hungarian method.

The Hungarian method is defined as a combinatorial optimization technique that solves the assignment problems in polynomial time and foreshadowed subsequent primal–dual approaches.

What are the steps involved in Hungarian method?

The following is a quick overview of the Hungarian method: Step 1: Subtract the row minima. Step 2: Subtract the column minimums. Step 3: Use a limited number of lines to cover all zeros. Step 4: Add some more zeros to the equation.

What is the purpose of the Hungarian method?

When workers are assigned to certain activities based on cost, the Hungarian method is beneficial for identifying minimum costs.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

www.springer.com The European Mathematical Society

• StatProb Collection
• Recent changes
• Current events
• Random page
• Project talk
• Request account
• What links here
• Related changes
• Special pages
• Printable version
• Permanent link
• Page information
• View source

Assignment problem

The problem of optimally assigning $ m $ individuals to $ m $ jobs. It can be formulated as a linear programming problem that is a special case of the transport problem :

maximize $ \sum _ {i,j } c _ {ij } x _ {ij } $

$$ \sum _ { j } x _ {ij } = a _ {i} , i = 1 \dots m $$

(origins or supply),

$$ \sum _ { i } x _ {ij } = b _ {j} , j = 1 \dots n $$

(destinations or demand), where $ x _ {ij } \geq 0 $ and $ \sum a _ {i} = \sum b _ {j} $, which is called the balance condition. The assignment problem arises when $ m = n $ and all $ a _ {i} $ and $ b _ {j} $ are $ 1 $.

If all $ a _ {i} $ and $ b _ {j} $ in the transposed problem are integers, then there is an optimal solution for which all $ x _ {ij } $ are integers (Dantzig's theorem on integral solutions of the transport problem).

In the assignment problem, for such a solution $ x _ {ij } $ is either zero or one; $ x _ {ij } = 1 $ means that person $ i $ is assigned to job $ j $; the weight $ c _ {ij } $ is the utility of person $ i $ assigned to job $ j $.

The special structure of the transport problem and the assignment problem makes it possible to use algorithms that are more efficient than the simplex method . Some of these use the Hungarian method (see, e.g., [a5] , [a1] , Chapt. 7), which is based on the König–Egervary theorem (see König theorem ), the method of potentials (see [a1] , [a2] ), the out-of-kilter algorithm (see, e.g., [a3] ) or the transportation simplex method.

In turn, the transportation problem is a special case of the network optimization problem.

A totally different assignment problem is the pole assignment problem in control theory.

• This page was last edited on 5 April 2020, at 18:48.
• Privacy policy
• About Encyclopedia of Mathematics
• Disclaimers
• Impressum-Legal

Procedure, Example Solved Problem | Operations Research - Solution of assignment problems (Hungarian Method) | 12th Business Maths and Statistics : Chapter 10 : Operations Research

Chapter: 12th business maths and statistics : chapter 10 : operations research.

Solution of assignment problems (Hungarian Method)

First check whether the number of rows is equal to the numbers of columns, if it is so, the assignment problem is said to be balanced.

Step :1 Choose the least element in each row and subtract it from all the elements of that row.

Step :2 Choose the least element in each column and subtract it from all the elements of that column. Step 2 has to be performed from the table obtained in step 1.

Step:3 Check whether there is atleast one zero in each row and each column and make an assignment as follows.

Step :4 If each row and each column contains exactly one assignment, then the solution is optimal.

Example 10.7

Solve the following assignment problem. Cell values represent cost of assigning job A, B, C and D to the machines I, II, III and IV.

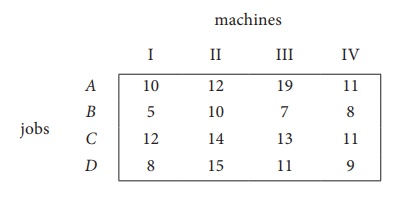
Here the number of rows and columns are equal.

∴ The given assignment problem is balanced. Now let us find the solution.

Step 1: Select a smallest element in each row and subtract this from all the elements in its row.

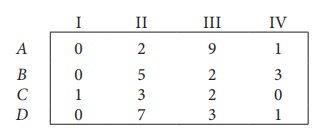
Look for atleast one zero in each row and each column.Otherwise go to step 2.

Step 2: Select the smallest element in each column and subtract this from all the elements in its column.

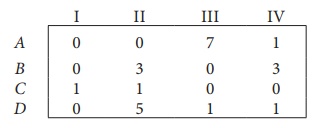
Since each row and column contains atleast one zero, assignments can be made.

Step 3 (Assignment):

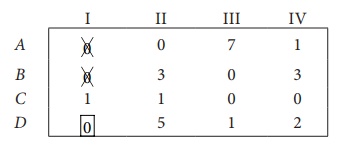
Thus all the four assignments have been made. The optimal assignment schedule and total cost is

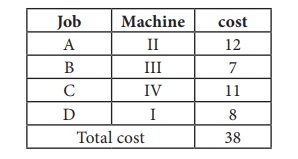
The optimal assignment (minimum) cost

Example 10.8

Consider the problem of assigning five jobs to five persons. The assignment costs are given as follows. Determine the optimum assignment schedule.

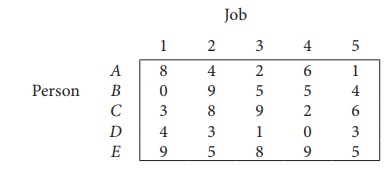
∴ The given assignment problem is balanced.

Now let us find the solution.

The cost matrix of the given assignment problem is

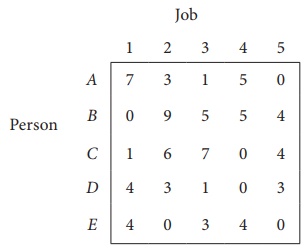
Column 3 contains no zero. Go to Step 2.

Thus all the five assignments have been made. The Optimal assignment schedule and total cost is

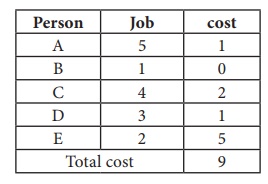
The optimal assignment (minimum) cost = ` 9

Example 10.9

Solve the following assignment problem.

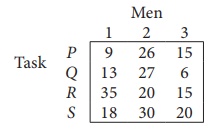
Since the number of columns is less than the number of rows, given assignment problem is unbalanced one. To balance it , introduce a dummy column with all the entries zero. The revised assignment problem is

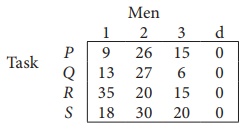
Here only 3 tasks can be assigned to 3 men.

Step 1: is not necessary, since each row contains zero entry. Go to Step 2.

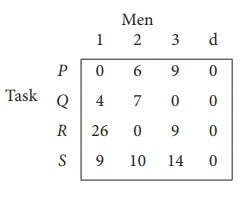
Step 3 (Assignment) :

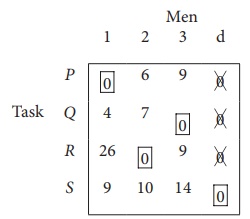
Since each row and each columncontains exactly one assignment,all the three men have been assigned a task. But task S is not assigned to any Man. The optimal assignment schedule and total cost is

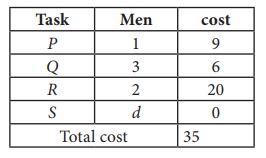
The optimal assignment (minimum) cost = ₹ 35

Related Topics

Privacy Policy , Terms and Conditions , DMCA Policy and Compliant

Copyright © 2018-2024 BrainKart.com; All Rights Reserved. Developed by Therithal info, Chennai.

Nash Balanced Assignment Problem

• Conference paper
• First Online: 21 November 2022
• Cite this conference paper

• Minh Hieu Nguyen 11 ,
• Mourad Baiou 11 &
• Viet Hung Nguyen 11  

Part of the book series: Lecture Notes in Computer Science ((LNCS,volume 13526))

Included in the following conference series:

• International Symposium on Combinatorial Optimization

358 Accesses

2 Citations

In this paper, we consider a variant of the classic Assignment Problem (AP), called the Balanced Assignment Problem (BAP) [ 2 ]. The BAP seeks to find an assignment solution which has the smallest value of max-min distance : the difference between the maximum assignment cost and the minimum one. However, by minimizing only the max-min distance, the total cost of the BAP solution is neglected and it may lead to an inefficient solution in terms of total cost. Hence, we propose a fair way based on Nash equilibrium [ 1 , 3 , 4 ] to inject the total cost into the objective function of the BAP for finding assignment solutions having a better trade-off between the two objectives: the first aims at minimizing the total cost and the second aims at minimizing the max-min distance. For this purpose, we introduce the concept of Nash Fairness (NF) solutions based on the definition of proportional-fair scheduling adapted in the context of the AP: a transfer of utilities between the total cost and the max-min distance is considered to be fair if the percentage increase in the total cost is smaller than the percentage decrease in the max-min distance and vice versa.

We first show the existence of a NF solution for the AP which is exactly the optimal solution minimizing the product of the total cost and the max-min distance. However, finding such a solution may be difficult as it requires to minimize a concave function. The main result of this paper is to show that finding all NF solutions can be done in polynomial time. For that, we propose a Newton-based iterative algorithm converging to NF solutions in polynomial time. It consists in optimizing a sequence of linear combinations of the two objective based on Weighted Sum Method [ 5 ]. Computational results on various instances of the AP are presented and commented.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

The fair owa one-to-one assignment problem: np-hardness and polynomial time special cases.

An Efficient Primal-Dual Algorithm for Fair Combinatorial Optimization Problems

Restricted Max-Min Allocation: Integrality Gap and Approximation Algorithm

Bertsimas, D., Farias, V.F., Trichakis, N.: The price of fairness. Oper. Res. January–February 59 (1), 17–31 (2011)

MathSciNet   MATH   Google Scholar  

Martello, S., Pulleyblank, W.R., Toth, P., De Werra, D.: Balanced optimization problems. Oper. Res. Lett. 3 (5), 275–278 (1984)

Article   MathSciNet   MATH   Google Scholar  

Kelly, F.P., Maullo, A.K., Tan, D.K.H.: Rate control for communication networks: shadow prices, proportional fairness and stability. J. Oper. Res. Soc. 49 (3), 237–252 (1997). https://doi.org/10.1057/palgrave.jors.2600523

Article   Google Scholar  

Ogryczak, W., Luss, H., Pioro, M., Nace, D., Tomaszewski, A.: Fair optimization and networks: a survey. J. Appl. Math. 2014 , 1–26 (2014)

Marler, R.T., Arora, J.S.: The weighted sum method for multi-objective optimization: new insights. Struct. Multi. Optim. 41 (6), 853–862 (2010)

Heller, I., Tompkins, C.B.: An extension of a theorem of Dantzig’s. Ann. Math. Stud. (38), 247–254 (1956)

Google Scholar  

Kuhn, H.W.: The Hungarian method for assignment problem. Naval Res. Logist. Q. 2 (1–2), 83–97 (1955)

Martello, S.: Most and least uniform spanning trees. Discrete Appl. Math. 15 (2), 181–197 (1986)

Beasley, J.E.: Linear programming on Clay supercomputer. J. Oper. Res. Soc. 41 , 133–139 (1990)

Nguyen, M.H, Baiou, M., Nguyen, V.H., Vo, T.Q.T.: Nash fairness solutions for balanced TSP. In: International Network Optimization Conference (INOC2022) (2022)

Download references

Author information

Authors and affiliations.

INP Clermont Auvergne, Univ Clermont Auvergne, Mines Saint-Etienne, CNRS, UMR 6158 LIMOS, 1 Rue de la Chebarde, Aubiere Cedex, France

Minh Hieu Nguyen, Mourad Baiou & Viet Hung Nguyen

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Viet Hung Nguyen .

Editor information

Editors and affiliations.

ESSEC Business School of Paris, Cergy Pontoise Cedex, France

Ivana Ljubić

IBM TJ Watson Research Center, Yorktown Heights, NY, USA

Francisco Barahona

Georgia Institute of Technology, Atlanta, GA, USA

Santanu S. Dey

Université Paris-Dauphine, Paris, France

A. Ridha Mahjoub

Proposition 1 . There may be more than one NF solution for the AP.

Let us illustrate this by an instance of the AP having the following cost matrix

By verifying all feasible assignment solutions in this instance, we obtain easily three assignment solutions \((1-1, 2-2, 3-3), (1-2, 2-3, 3-1)\) , \((1-3, 2-2, 3-1)\) and \((1-3, 2-1, 3-2)\) corresponding to 4 NF solutions (280, 36), (320, 32), (340, 30) and (364, 28). Note that \(i-j\) where \(1 \le i,j \le 3\) represents the assignment between worker i and job j in the solution of this instance.     \(\square \)

We recall below the proofs of some recent results that we have published in [ 10 ]. They are needed to prove the new results presented in this paper.

Theorem 2 [ 10 ] . \((P^{*},Q^{*}) = {{\,\mathrm{arg\,min}\,}}_{(P,Q) \in \mathcal {S}} PQ\) is a NF solution.

Obviously, there always exists a solution \((P^{*},Q^{*}) \in \mathcal {S}\) such that

Now \(\forall (P',Q') \in \mathcal {S}\) we have \(P'Q' \ge P^{*}Q^{*}\) . Then

The first inequality holds by the Cauchy-Schwarz inequality.

Hence, \((P^{*},Q^{*})\) is a NF solution.     \(\square \)

Theorem 3 [ 10 ] . \((P^{*},Q^{*}) \in \mathcal {S}\) is a NF solution if and only if \((P^{*},Q^{*})\) is an optimal solution of \(\mathcal {P(\alpha ^{*})}\) where \(\alpha ^{*} = \frac{Q^{*}}{P^{*}}\) .

Firstly, let \((P^{*},Q^{*})\) be a NF solution and \(\alpha ^{*} = \frac{Q^{*}}{P^{*}}\) . We will show that \((P^{*},Q^{*})\) is an optimal solution of \(\mathcal {P(\alpha ^{*})}\) .

Since \((P^{*},Q^{*})\) is a NF solution, we have

Since \(\alpha ^{*} = \frac{Q^{*}}{P^{*}}\) , we have \(\alpha ^{*}P^{*}+Q^{*} = 2Q^{*}\) .

Dividing two sides of ( 6 ) by \(P^{*} > 0\) we obtain

So we deduce from ( 7 )

Hence, \((P^{*},Q^{*})\) is an optimal solution of \(\mathcal {P}(\alpha ^{*})\) .

Now suppose \(\alpha ^{*} = \frac{Q^{*}}{P^{*}}\) and \((P^{*},Q^{*})\) is an optimal solution of \(\mathcal {P}(\alpha ^{*})\) , we show that \((P^{*},Q^{*})\) is a NF solution.

If \((P^{*},Q^{*})\) is not a NF solution, there exists a solution \((P',Q') \in \mathcal {S}\) such that

We have then

which contradicts the optimality of \((P^{*},Q^{*})\) .     \(\square \)

Lemma 3 [ 10 ] . Let \(\alpha , \alpha ' \in \mathbb {R}_+\) and \((P_{\alpha }, Q_{\alpha })\) , \((P_{\alpha '}, Q_{\alpha '})\) be the optimal solutions of \(\mathcal {P(\alpha )}\) and \(\mathcal {P(\alpha ')}\) respectively, if \(\alpha \le \alpha '\) then \(P_{\alpha } \ge P_{\alpha '}\) and \(Q_{\alpha } \le Q_{\alpha '}\) .

The optimality of \((P_{\alpha }, Q_{\alpha })\) and \((P_{\alpha '}, Q_{\alpha '})\) gives

By adding both sides of ( 8a ) and ( 8b ), we obtain \((\alpha - \alpha ') (P_{\alpha } - P_{\alpha '}) \le 0\) . Since \(\alpha \le \alpha '\) , it follows that \(P_{\alpha } \ge P_{\alpha '}\) .

On the other hand, inequality ( 8a ) implies \(Q_{\alpha '} - Q_{\alpha } \ge \alpha (P_{\alpha } - P_{\alpha '}) \ge 0\) that leads to \(Q_{\alpha } \le Q_{\alpha '}\) .     \(\square \)

Lemma 4 [ 10 ] . During the execution of Procedure Find ( \(\alpha _{0})\) in Algorithm 1 , \(\alpha _{i} \in [0,1], \, \forall i \ge 1\) . Moreover, if \(T_{0} \ge 0\) then the sequence \(\{\alpha _i\}\) is non-increasing and \(T_{i} \ge 0, \, \forall i \ge 0\) . Otherwise, if \(T_{0} \le 0\) then the sequence \(\{\alpha _i\}\) is non-decreasing and \(T_{i} \le 0, \, \forall i \ge 0\) .

Since \(P \ge Q \ge 0, \, \forall (P, Q) \in \mathcal {S}\) , it follows that \(\alpha _{i+1} = \frac{Q_i}{P_i} \in [0,1], \, \forall i \ge 0\) .

We first consider \(T_{0} \ge 0\) . We proof \(\alpha _i \ge \alpha _{i+1}, \, \forall i \ge 0\) by induction on i . For \(i = 0\) , we have \(T_{0} = \alpha _{0} P_{0} - Q_{0} = P_{0}(\alpha _{0}-\alpha _{1}) \ge 0\) , it follows that \(\alpha _{0} \ge \alpha _{1}\) . Suppose that our hypothesis is true until \(i = k \ge 0\) , we will prove that it is also true with \(i = k+1\) .

Indeed, we have

The inductive hypothesis gives \(\alpha _k \ge \alpha _{k+1}\) that implies \(P_{k+1} \ge P_k > 0\) and \(Q_{k} \ge Q_{k+1} \ge 0\) according to Lemma 3 . It leads to \(Q_{k}P_{k+1} - P_{k}Q_{k+1} \ge 0\) and then \(\alpha _{k+1} - \alpha _{k+2} \ge 0\) .

Hence, we have \(\alpha _{i} \ge \alpha _{i+1}, \, \forall i \ge 0\) .

Consequently, \(T_{i} = \alpha _{i}P_{i} - Q_{i} = P_{i}(\alpha _{i}-\alpha _{i+1}) \ge 0, \, \forall i \ge 0\) .

Similarly, if \(T_{0} \le 0\) we obtain that the sequence \(\{\alpha _i\}\) is non-decreasing and \(T_{i} \le 0, \, \forall i \ge 0\) . That concludes the proof.     \(\square \)

Lemma 5 [ 10 ] . From each \(\alpha _{0} \in [0,1]\) , Procedure Find \((\alpha _{0})\) converges to a coefficient \(\alpha _{k} \in \mathcal {C}_{0}\) satisfying \(\alpha _{k}\) is the unique element \(\in \mathcal {C}_{0}\) between \(\alpha _{0}\) and \(\alpha _{k}\) .

As a consequence of Lemma 4 , Procedure \(\textit{Find}(\alpha _{0})\) converges to a coefficient \(\alpha _{k} \in [0,1], \forall \alpha _{0} \in [0,1]\) .

By the stopping criteria of Procedure Find \((\alpha _{0})\) , when \(T_{k} = \alpha _{k} P_{k} - Q_{k} = 0\) we obtain \(\alpha _{k} \in C_{0}\) and \((P_{k},Q_{k})\) is a NF solution. (Theorem 3 )

If \(T_{0} = 0\) then obviously \(\alpha _{k} = \alpha _{0}\) . We consider \(T_{0} > 0\) and the sequence \(\{\alpha _i\}\) is now non-negative, non-increasing. We will show that \([\alpha _{k},\alpha _{0}] \cap \mathcal {C}_{0} = \alpha _{k}\) .

Suppose that we have \(\alpha \in (\alpha _{k},\alpha _{0}]\) and \(\alpha \in \mathcal {C}_{0}\) corresponding to a NF solution ( P ,  Q ). Then there exists \(1 \le i \le k\) such that \(\alpha \in (\alpha _{i}, \alpha _{i-1}]\) . Since \(\alpha \le \alpha _{i-1}\) , \(P \ge P_{i-1}\) and \(Q \le Q_{i-1}\) due to Lemma 3 . Thus, we get

By the definitions of \(\alpha \) and \(\alpha _{i}\) , inequality ( 9 ) is equivalent to \(\alpha \le \alpha _{i}\) which leads to a contradiction.

By repeating the same argument for \(T_{0} < 0\) , we also have a contradiction.     \(\square \)

Rights and permissions

Reprints and permissions

Copyright information

© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG

About this paper

Cite this paper.

Nguyen, M.H., Baiou, M., Nguyen, V.H. (2022). Nash Balanced Assignment Problem. In: Ljubić, I., Barahona, F., Dey, S.S., Mahjoub, A.R. (eds) Combinatorial Optimization. ISCO 2022. Lecture Notes in Computer Science, vol 13526. Springer, Cham. https://doi.org/10.1007/978-3-031-18530-4_13

Download citation

DOI : https://doi.org/10.1007/978-3-031-18530-4_13

Published : 21 November 2022

Publisher Name : Springer, Cham

Print ISBN : 978-3-031-18529-8

Online ISBN : 978-3-031-18530-4

eBook Packages : Computer Science Computer Science (R0)

Share this paper

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

• Branch and Bound Tutorial
• Backtracking Vs Branch-N-Bound
• 0/1 Knapsack
• 8 Puzzle Problem
• Job Assignment Problem
• N-Queen Problem
• Travelling Salesman Problem
• Branch and Bound Algorithm
• Introduction to Branch and Bound - Data Structures and Algorithms Tutorial
• 0/1 Knapsack using Branch and Bound
• Implementation of 0/1 Knapsack using Branch and Bound
• 8 puzzle Problem using Branch And Bound

Job Assignment Problem using Branch And Bound

• N Queen Problem using Branch And Bound
• Traveling Salesman Problem using Branch And Bound

Let there be N workers and N jobs. Any worker can be assigned to perform any job, incurring some cost that may vary depending on the work-job assignment. It is required to perform all jobs by assigning exactly one worker to each job and exactly one job to each agent in such a way that the total cost of the assignment is minimized.

Let us explore all approaches for this problem.

Solution 1: Brute Force  

We generate n! possible job assignments and for each such assignment, we compute its total cost and return the less expensive assignment. Since the solution is a permutation of the n jobs, its complexity is O(n!).

Solution 2: Hungarian Algorithm  

The optimal assignment can be found using the Hungarian algorithm. The Hungarian algorithm has worst case run-time complexity of O(n^3).

Solution 3: DFS/BFS on state space tree  

A state space tree is a N-ary tree with property that any path from root to leaf node holds one of many solutions to given problem. We can perform depth-first search on state space tree and but successive moves can take us away from the goal rather than bringing closer. The search of state space tree follows leftmost path from the root regardless of initial state. An answer node may never be found in this approach. We can also perform a Breadth-first search on state space tree. But no matter what the initial state is, the algorithm attempts the same sequence of moves like DFS.

Solution 4: Finding Optimal Solution using Branch and Bound  

The selection rule for the next node in BFS and DFS is “blind”. i.e. the selection rule does not give any preference to a node that has a very good chance of getting the search to an answer node quickly. The search for an optimal solution can often be speeded by using an “intelligent” ranking function, also called an approximate cost function to avoid searching in sub-trees that do not contain an optimal solution. It is similar to BFS-like search but with one major optimization. Instead of following FIFO order, we choose a live node with least cost. We may not get optimal solution by following node with least promising cost, but it will provide very good chance of getting the search to an answer node quickly.

There are two approaches to calculate the cost function:  

• For each worker, we choose job with minimum cost from list of unassigned jobs (take minimum entry from each row).
• For each job, we choose a worker with lowest cost for that job from list of unassigned workers (take minimum entry from each column).

In this article, the first approach is followed.

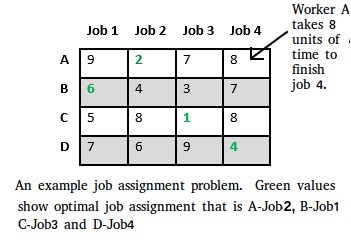
Let’s take below example and try to calculate promising cost when Job 2 is assigned to worker A. 

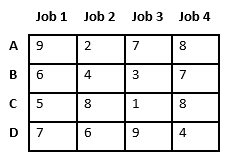
Since Job 2 is assigned to worker A (marked in green), cost becomes 2 and Job 2 and worker A becomes unavailable (marked in red). 

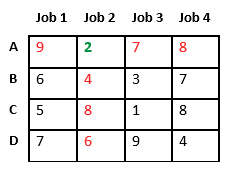
Now we assign job 3 to worker B as it has minimum cost from list of unassigned jobs. Cost becomes 2 + 3 = 5 and Job 3 and worker B also becomes unavailable. 

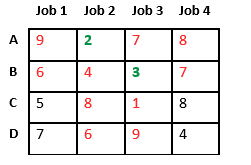
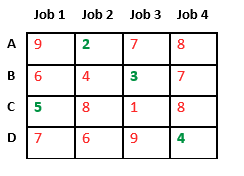
Finally, job 1 gets assigned to worker C as it has minimum cost among unassigned jobs and job 4 gets assigned to worker D as it is only Job left. Total cost becomes 2 + 3 + 5 + 4 = 14. 

Below diagram shows complete search space diagram showing optimal solution path in green. 

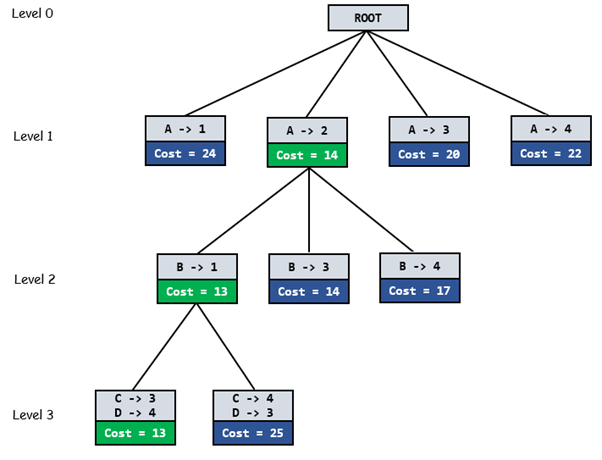
Complete Algorithm:  

Below is the implementation of the above approach:

Time Complexity: O(M*N). This is because the algorithm uses a double for loop to iterate through the M x N matrix.  Auxiliary Space: O(M+N). This is because it uses two arrays of size M and N to track the applicants and jobs.

Please Login to comment...

Similar reads.

• Branch and Bound

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

OPERATIONS RESEARCH

Lesson 9. solution of assignment problem.

Current course

Assignment Problem: Linear Programming

The assignment problem is a special type of transportation problem , where the objective is to minimize the cost or time of completing a number of jobs by a number of persons.

In other words, when the problem involves the allocation of n different facilities to n different tasks, it is often termed as an assignment problem.

The model's primary usefulness is for planning. The assignment problem also encompasses an important sub-class of so-called shortest- (or longest-) route models. The assignment model is useful in solving problems such as, assignment of machines to jobs, assignment of salesmen to sales territories, travelling salesman problem, etc.

It may be noted that with n facilities and n jobs, there are n! possible assignments. One way of finding an optimal assignment is to write all the n! possible arrangements, evaluate their total cost, and select the assignment with minimum cost. But, due to heavy computational burden this method is not suitable. This chapter concentrates on an efficient method for solving assignment problems that was developed by a Hungarian mathematician D.Konig.

"A mathematician is a device for turning coffee into theorems." -Paul Erdos

Formulation of an assignment problem

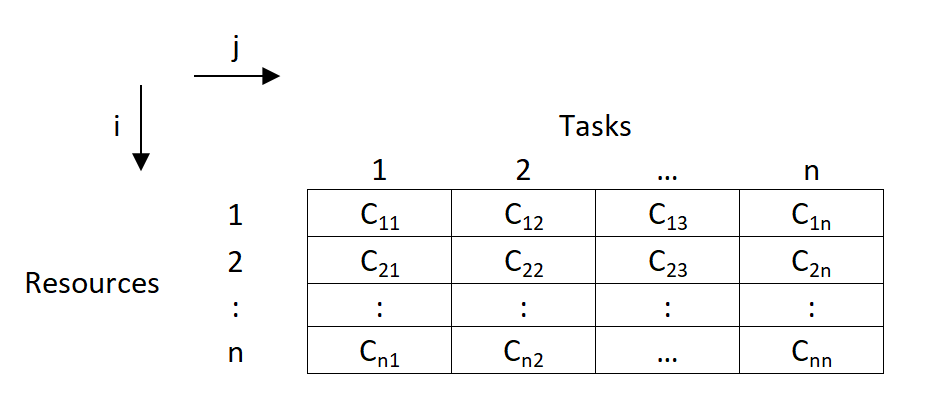
Suppose a company has n persons of different capacities available for performing each different job in the concern, and there are the same number of jobs of different types. One person can be given one and only one job. The objective of this assignment problem is to assign n persons to n jobs, so as to minimize the total assignment cost. The cost matrix for this problem is given below:

The structure of an assignment problem is identical to that of a transportation problem.

To formulate the assignment problem in mathematical programming terms , we define the activity variables as

for i = 1, 2, ..., n and j = 1, 2, ..., n

In the above table, c ij is the cost of performing jth job by ith worker.

Generalized Form of an Assignment Problem

The optimization model is

Minimize c 11 x 11 + c 12 x 12 + ------- + c nn x nn

subject to x i1 + x i2 +..........+ x in = 1          i = 1, 2,......., n x 1j + x 2j +..........+ x nj = 1          j = 1, 2,......., n

x ij = 0 or 1

In Σ Sigma notation

x ij = 0 or 1 for all i and j

An assignment problem can be solved by transportation methods, but due to high degree of degeneracy the usual computational techniques of a transportation problem become very inefficient. Therefore, a special method is available for solving such type of problems in a more efficient way.

Assumptions in Assignment Problem

• Number of jobs is equal to the number of machines or persons.
• Each man or machine is assigned only one job.
• Each man or machine is independently capable of handling any job to be done.
• Assigning criteria is clearly specified (minimizing cost or maximizing profit).

Share this article with your friends

Operations Research Simplified Back Next

Goal programming Linear programming Simplex Method Transportation Problem

Unbalanced Assignment Problem: Definition, Formulation, and Solution Methods

Table of Contents

Are you familiar with the assignment problem in Operations Research (OR)? This problem deals with assigning tasks to workers in a way that minimizes the total cost or time needed to complete the tasks. But what if the number of tasks and workers is not equal? In this case, we face the Unbalanced Assignment Problem (UAP). This blog will help you understand what the UAP is, how to formulate it, and how to solve it.

What is the Unbalanced Assignment Problem?

The Unbalanced Assignment Problem is an extension of the Assignment Problem in OR, where the number of tasks and workers is not equal. In the UAP, some tasks may remain unassigned, while some workers may not be assigned any task. The objective is still to minimize the total cost or time required to complete the assigned tasks, but the UAP has additional constraints that make it more complex than the traditional assignment problem.

Formulation of the Unbalanced Assignment Problem

To formulate the UAP, we start with a matrix that represents the cost or time required to assign each task to each worker. If the matrix is square, we can use the Hungarian algorithm to solve the problem. But when the matrix is not square, we need to add dummy tasks or workers to balance the matrix. These dummy tasks or workers have zero costs and are used to make the matrix square.

Once we have a square matrix, we can apply the Hungarian algorithm to find the optimal assignment. However, we need to be careful in interpreting the results, as the assignment may include dummy tasks or workers that are not actually assigned to anything.

Solutions for the Unbalanced Assignment Problem

Besides the Hungarian algorithm, there are other methods to solve the UAP, such as the transportation algorithm and the auction algorithm. The transportation algorithm is based on transforming the UAP into a transportation problem, which can be solved with the transportation simplex method. The auction algorithm is an iterative method that simulates a bidding process between the tasks and workers to find the optimal assignment.

In summary, the Unbalanced Assignment Problem is a variant of the traditional Assignment Problem in OR that deals with assigning tasks to workers when the number of tasks and workers is not equal. To solve the UAP, we need to balance the matrix by adding dummy tasks or workers and then apply algorithms such as the Hungarian algorithm, the transportation algorithm, or the auction algorithm. Understanding the UAP can help businesses and organizations optimize their resource allocation and improve their operational efficiency.

How useful was this post?

Click on a star to rate it!

Average rating 1.5 / 5. Vote count: 2

No votes so far! Be the first to rate this post.

We are sorry that this post was not useful for you! 😔

Let us improve this post!

Tell us how we can improve this post?

Operations Research

1 Operations Research-An Overview

• History of O.R.
• Approach, Techniques and Tools
• Phases and Processes of O.R. Study
• Typical Applications of O.R
• Limitations of Operations Research
• Models in Operations Research
• O.R. in real world

2 Linear Programming: Formulation and Graphical Method

• General formulation of Linear Programming Problem
• Optimisation Models
• Basics of Graphic Method
• Important steps to draw graph
• Multiple, Unbounded Solution and Infeasible Problems
• Solving Linear Programming Graphically Using Computer
• Application of Linear Programming in Business and Industry

3 Linear Programming-Simplex Method

• Principle of Simplex Method
• Computational aspect of Simplex Method
• Simplex Method with several Decision Variables
• Two Phase and M-method
• Multiple Solution, Unbounded Solution and Infeasible Problem
• Sensitivity Analysis
• Dual Linear Programming Problem

4 Transportation Problem

• Basic Feasible Solution of a Transportation Problem
• Modified Distribution Method
• Stepping Stone Method
• Unbalanced Transportation Problem
• Degenerate Transportation Problem
• Transhipment Problem
• Maximisation in a Transportation Problem

5 Assignment Problem

• Solution of the Assignment Problem
• Unbalanced Assignment Problem
• Problem with some Infeasible Assignments
• Maximisation in an Assignment Problem
• Crew Assignment Problem

6 Application of Excel Solver to Solve LPP

• Building Excel model for solving LP: An Illustrative Example

7 Goal Programming

• Concepts of goal programming
• Goal programming model formulation
• Graphical method of goal programming
• The simplex method of goal programming
• Using Excel Solver to Solve Goal Programming Models
• Application areas of goal programming

8 Integer Programming

• Some Integer Programming Formulation Techniques
• Binary Representation of General Integer Variables
• Unimodularity
• Cutting Plane Method
• Branch and Bound Method
• Solver Solution

9 Dynamic Programming

• Dynamic Programming Methodology: An Example
• Definitions and Notations
• Dynamic Programming Applications

10 Non-Linear Programming

• Solution of a Non-linear Programming Problem
• Convex and Concave Functions
• Kuhn-Tucker Conditions for Constrained Optimisation
• Quadratic Programming
• Separable Programming
• NLP Models with Solver

11 Introduction to game theory and its Applications

• Important terms in Game Theory
• Saddle points
• Mixed strategies: Games without saddle points
• 2 x n games
• Exploiting an opponent’s mistakes

12 Monte Carlo Simulation

• Reasons for using simulation
• Monte Carlo simulation
• Limitations of simulation
• Steps in the simulation process
• Some practical applications of simulation
• Two typical examples of hand-computed simulation
• Computer simulation

13 Queueing Models

• Characteristics of a queueing model
• Notations and Symbols
• Statistical methods in queueing
• The M/M/I System
• The M/M/C System
• The M/Ek/I System
• Decision problems in queueing

Assignment Model | Linear Programming Problem (LPP) | Introduction

What is assignment model.

→ Assignment model is a special application of Linear Programming Problem (LPP) , in which the main objective is to assign the work or task to a group of individuals such that;

i) There is only one assignment.

ii) All the assignments should be done in such a way that the overall cost is minimized (or profit is maximized, incase of maximization).

→ In assignment problem, the cost of performing each task by each individual is known. → It is desired to find out the best assignments, such that overall cost of assigning the work is minimized.

For example:

Suppose there are 'n' tasks, which are required to be performed using 'n' resources.

The cost of performing each task by each resource is also known (shown in cells of matrix)

• In the above asignment problem, we have to provide assignments such that there is one to one assignments and the overall cost is minimized.

How Assignment Problem is related to LPP? OR Write mathematical formulation of Assignment Model.

→ Assignment Model is a special application of Linear Programming (LP).

→ The mathematical formulation for Assignment Model is given below:

→ Let, C i j \text {C}_{ij} C ij ​ denotes the cost of resources 'i' to the task 'j' ; such that

→ Now assignment problems are of the Minimization type. So, our objective function is to minimize the overall cost.

→ Subjected to constraint;

(i) For all j t h j^{th} j t h task, only one i t h i^{th} i t h resource is possible:

(ii) For all i t h i^{th} i t h resource, there is only one j t h j^{th} j t h task possible;

(iii) x i j x_{ij} x ij ​ is '0' or '1'.

Types of Assignment Problem:

(i) balanced assignment problem.

• It consist of a suqare matrix (n x n).
• Number of rows = Number of columns

(ii) Unbalanced Assignment Problem

• It consist of a Non-square matrix.
• Number of rows ≠ \not=  = Number of columns

Methods to solve Assignment Model:

(i) integer programming method:.

In assignment problem, either allocation is done to the cell or not.

So this can be formulated using 0 or 1 integer.

While using this method, we will have n x n decision varables, and n+n equalities.

So even for 4 x 4 matrix problem, it will have 16 decision variables and 8 equalities.

So this method becomes very lengthy and difficult to solve.

(ii) Transportation Methods:

As assignment problem is a special case of transportation problem, it can also be solved using transportation methods.

In transportation methods ( NWCM , LCM & VAM), the total number of allocations will be (m+n-1) and the solution is known as non-degenerated. (For eg: for 3 x 3 matrix, there will be 3+3-1 = 5 allocations)

But, here in assignment problems, the matrix is a square matrix (m=n).

So total allocations should be (n+n-1), i.e. for 3 x 3 matrix, it should be (3+3-1) = 5

But, we know that in 3 x 3 assignment problem, maximum possible possible assignments are 3 only.

So, if are we will use transportation methods, then the solution will be degenerated as it does not satisfy the condition of (m+n-1) allocations.

So, the method becomes lengthy and time consuming.

(iii) Enumeration Method:

It is a simple trail and error type method.

Consider a 3 x 3 assignment problem. Here the assignments are done randomly and the total cost is found out.

For 3 x 3 matrix, the total possible trails are 3! So total 3! = 3 x 2 x 1 = 6 trails are possible.

The assignments which gives minimum cost is selected as optimal solution.

But, such trail and error becomes very difficult and lengthy.

If there are more number of rows and columns, ( For eg: For 6 x 6 matrix, there will be 6! trails. So 6! = 6 x 5 x 4 x 3 x 2 x 1 = 720 trails possible) then such methods can't be applied for solving assignments problems.

(iv) Hungarian Method:

It was developed by two mathematicians of Hungary. So, it is known as Hungarian Method.

It is also know as Reduced matrix method or Flood's technique.

There are two main conditions for applying Hungarian Method:

(1) Square Matrix (n x n). (2) Problem should be of minimization type.

Suggested Notes:

Modified Distribution Method (MODI) | Transportation Problem | Transportation Model

Stepping Stone | Transportation Problem | Transportation Model

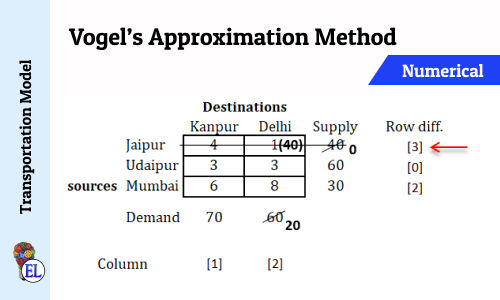
Vogel’s Approximation Method (VAM) | Method to Solve Transportation Problem | Transportation Model

Transportation Model - Introduction

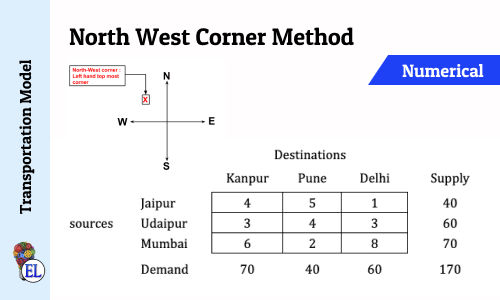
North West Corner Method | Method to Solve Transportation Problem | Transportation Model

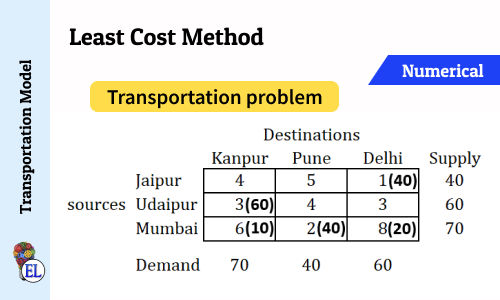
Least Cost Method | Method to Solve Transportation Problem | Transportation Model

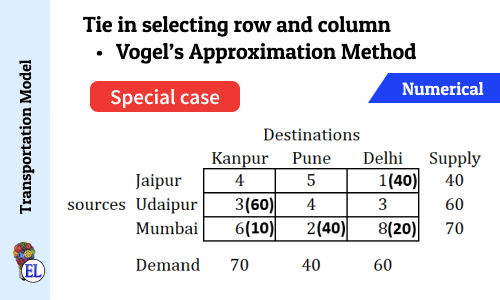
Tie in selecting row and column (Vogel's Approximation Method - VAM) | Numerical | Solving Transportation Problem | Transportation Model

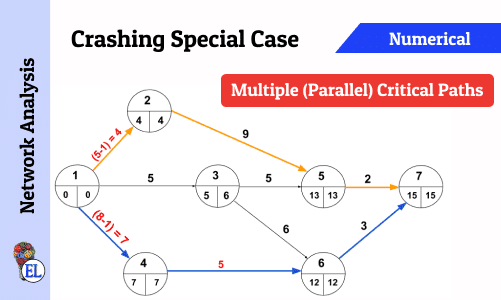
Crashing Special Case - Multiple (Parallel) Critical Paths

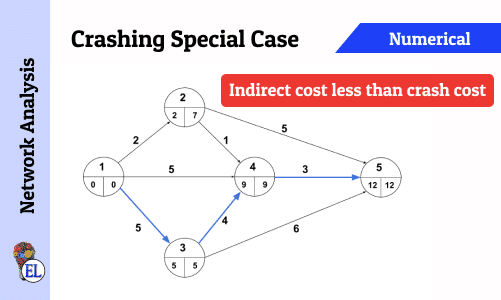
Crashing Special Case - Indirect cost less than Crash Cost

Basics of Program Evaluation and Review Technique (PERT)

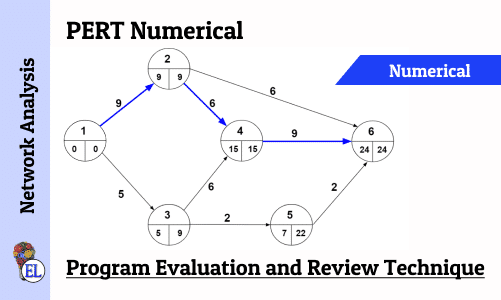
Numerical on PERT (Program Evaluation and Review Technique)

Network Analysis - Dealing with Network Construction Basics

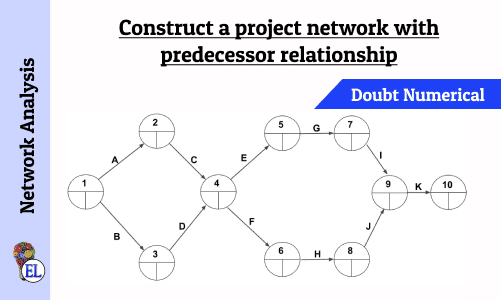
Construct a project network with predecessor relationship | Operation Research | Numerical

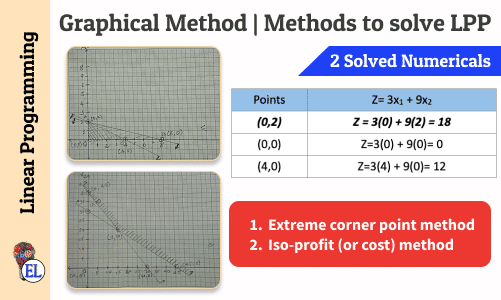
Graphical Method | Methods to solve LPP | Linear Programming

Basics of Linear Programming

Linear Programming Problem (LPP) Formulation with Numericals

All comments that you add will await moderation. We'll publish all comments that are topic related, and adhere to our Code of Conduct .

Want to tell us something privately? Contact Us

Post comment

Education Lessons

Stay in touch, [notes] operation research, [notes] dynamics of machinery, [notes] maths, [notes] science, [notes] computer aided design.

Follow Polygon online:

• Follow Polygon on Facebook
• Follow Polygon on Youtube
• Follow Polygon on Instagram

Site search

• Dragon’s Dogma 2
• Ghost of Tsushima
• Zelda: Tears of the Kingdom
• Baldur’s Gate 3
• GTA 5 cheats
• PlayStation
• Dungeons & Dragons
• Magic: The Gathering
• Board Games
• All Tabletop
• All Entertainment
• What to Watch
• What to Play
• Buyer’s Guides
• Really Bad Chess
• All Puzzles

Filed under:

• Entertainment

The 3-body problem is real, and it’s really unsolvable

Oh god don’t make me explain math

Share this story

• Share this on Facebook
• Share this on Reddit
• Share All sharing options

Share All sharing options for: The 3-body problem is real, and it’s really unsolvable

Everybody seems to be talking about 3 Body Problem , the new Netflix series based on Cixin Liu’s Remembrance of Earth’s Past book trilogy . Fewer people are talking about the two series’ namesake: The unsolvable physics problem of the same name.

This makes sense, because it’s confusing . In physics, the three-body problem attempts to find a way to predict the movements of three objects whose gravity interacts with each of the others — like three stars that are close together in space. Sounds simple enough, right? Yet I myself recently pulled up the Wikipedia article on the three-body problem and closed the tab in the same manner that a person might stagger away from a bright light. Apparently the Earth, sun, and moon are a three-body system? Are you telling me we don’t know how the moon moves ? Scientists have published multiple solutions for the three-body problem? Are you telling me Cixin Liu’s books are out of date?

All I’d wanted to know was why the problem was considered unsolvable, and now memories of my one semester of high school physics were swimming before my eyes like so many glowing doom numbers. However, despite my pains, I have readied several ways that we non-physicists can be confident that the three-body problem is, in fact, unsolvable.

Reason 1: This is a special definition of ‘unsolvable’

The three-body problem is extra confusing, because scientists are seemingly constantly finding new solutions to the three-body problem! They just don’t mean a one-solution-for-all solution. Such a formula does exist for a two-body system, and apparently Isaac Newton figured it out in 1687 . But systems with more than two bodies are, according to physicists, too chaotic (i.e., not in the sense of a child’s messy bedroom, but in the sense of “chaos theory”) to be corralled by a single solution.

When physicists say they have a new solution to the three-body problem, they mean that they’ve found a specific solution for three-body systems that have certain theoretical parameters. Don’t ask me to explain those parameters, because they’re all things like “the three masses are collinear at each instant” or “a zero angular momentum solution with three equal masses moving around a figure-eight shape.” But basically: By narrowing the focus of the problem to certain arrangements of three-body systems, physicists have been able to derive formulas that predict the movements of some of them, like in our solar system. The mass of the Earth and the sun create a “ restricted three-body problem ,” where a less-big body (in this case, the moon) moves under the influence of two massive ones (the Earth and the sun).

What physicists mean when they say the three-body problem has no solution is simply that there isn’t a one-formula-fits-all solution to every way that the gravity of three objects might cause those objects to move — which is exactly what Three-Body Problem bases its whole premise on.

Reason 2: 3 Body Problem picked an unsolved three-body system on purpose

Henri Poincaré’s research into a general solution to the three-body problem formed the basis of what would become known as chaos theory (you might know it from its co-starring role in Jurassic Park ). And 3 Body Problem itself isn’t about any old three-body system. It’s specifically about an extremely chaotic three-body system, the exact kind of arrangement of bodies that Poincaré was focused on when he showed that the problem is “unsolvable.”

[ Ed. note: The rest of this section includes some spoilers for 3 Body Problem .]

In both Liu’s books and Netflix’s 3 Body Problem , humanity faces an invasion by aliens (called Trisolarans in the English translation of the books, and San-Ti in the TV series) whose home solar system features three suns in a chaotic three-body relationship. It is a world where, unlike ours, the heavens are fundamentally unpredictable. Periods of icy cold give way to searing heat that give way to swings in gravity that turn into temporary reprieves that can never be trusted. The unpredictable nature of the San-Ti environment is the source of every detail of their physicality, their philosophy, and their desire to claim Earth for their own.

In other words, 3 Body Problem ’s three-body problem is unsolvable because Liu wanted to write a story with an unsolvable three-body system, so he chose one of the three-body systems for which we have not discovered a solution, and might never.

Reason 3: Scientists are still working on the three-body problem

Perhaps the best reason I can give you to believe that the three-body problem is real, and is really unsolvable, is that some scientists published a whole set of new solutions for specific three-body systems very recently .

If physicists are still working on the three-body problem, we can safely assume that it has not been solved. Scientists, after all, are the real experts. And I am definitely not.

The next level of puzzles.

Take a break from your day by playing a puzzle or two! We’ve got SpellTower, Typeshift, crosswords, and more.

Sign up for the newsletter Patch Notes

A weekly roundup of the best things from Polygon

Just one more thing!

Please check your email to find a confirmation email, and follow the steps to confirm your humanity.

Oops. Something went wrong. Please enter a valid email and try again.

Loading comments...

How to finish ‘Zero Hour’ and get Outbreak Perfected in Destiny 2

Abbott Elementary’s season 3 finale, Jeopardy! Masters, and more

Ben Schwartz and other comedy greats join Make Some Noise season 3

Why is it Summer Game Fest and not Summer Games Fest (plural)?

Where to pre-order the Ursula’s Return expansion for Disney Lorcana

The top 5 times a remastered Phantom Menace trailer made me incorrectly go ‘Star Wars is so back’

Featured Topics

Featured series.

A series of random questions answered by Harvard experts.

Explore the Gazette

Read the latest.

‘I haven’t really had a proper weekend in a long time’

Party like it’s 2020

Study of Psychedelics in Society and Culture announces funding recipients

‘you can solve anything’.

Priyanka Pillai wants to take on big problems — and has learned how good design can help

Christina Pazzanese

Harvard Staff Writer

Niles Singer/Harvard Staff Photographer

Part of the Commencement 2024 series

A collection of stories covering Harvard University’s 373rd Commencement.

Growing up in India, Priyanka Pillai witnessed the immense and varied struggles many impoverished people faced in their daily lives, such as getting prenatal care and protecting children from labor exploitation.

As an undergraduate in Bangalore studying industrial design, she wondered whether good design could help ease at least parts of these and other challenges. She came to Harvard Graduate School of Design two years ago and got her answer, discovering she could take on big problems “that you don’t even realize … could be tackled with design.”

Pillai wanted to do something to help address the refugee crisis in Uganda for her independent design engineering project. Those projects span two semesters and call for students seeking a master’s in design engineering (a joint GSD and John A. Paulson School of Engineering and Applied Sciences program) to identify complex, real-world problems and develop solution prototypes.

“For the first time, I truly felt like I was doing work that was very in touch with what GSD wants people to do, which is working with communities.”

Conducting fieldwork in Uganda, Pillai saw the difficulties that South Sudanese refugees were having reuniting with their families. The plight of those fleeing the ongoing civil war in the northeast African nation has become one of the largest refugee crises in the world, with more than half a million living in Uganda alone, mostly in camps.

More than 60 percent are children separated from parents who are looking for them, Pillai said, and need multiple layers of support. While non-governmental organizations (NGOs) are providing some assistance, much more help is needed.

“One thing that really stood out was agency. There’s currently a lack of agency when it comes to finding their family members on their own,” said Pillai, who graduates later this month. Many refugees use informal, ad hoc methods such as phone calls, WhatsApp, and photo sharing to try to find relatives.

“The second part, which is extremely critical, is that we need to move from a Western-centric way of finding a family member,” such as cataloguing names, ages, and date of separation done by NGOs, because it doesn’t capture vernacularor local geography, vital details that may speed up reunification, she said, noting that learning more about how to design for “the Indian context” and the Global South more generally was a key reason she came to Harvard.

“A lot of cultural nuances were missing in connection to the data to find missing family members,” she said. “And that’s the kind of solution that we’re moving toward.”

Given the ubiquity of cellphones there, Pillai and classmate Julius Stein designed and built an online platform for refugees to enter information about themselves using text, photos, and audio. The platform generates a series of questions that can lead to possible matches while minimizing the risk of exploitation by malign actors.

“For the first time, I truly felt like I was doing work that was very in touch with what GSD wants people to do, which is working with communities,” she said. “It was just a life-changing experience.”

Earlier this month, one startup Pillai is involved in, Alba, won an Ingenuity Award as part of the Harvard President’s Innovation Challenge. The team designed a special wipe so the visually impaired can better detect when their menstrual period has begun without relying on outside assistance.

In 2023, Pillai was part of a student project that won gold in the Spark International Design awards. The design team created Felt, a haptic armband that turns sound and visual clues into movement. The device assists people who are deaf blind to independently catch emotional nuances or subtexts in conversations, which often get lost in Braille or other translations.

During her time in the program, Pillai also jumped at the opportunity to take courses at the Harvard Kennedy School, Harvard Law School, and Harvard Graduate School of Education to learn more about things such as accessibility, ethical design, and negotiation.

“I knew that I was limiting myself because I didn’t know all these different things,” she said.

When not focused on her own studies, Pillai has been a teaching fellow for a design studio at GSD and at SEAS for a course led by her IDEP adviser, Krzysztof Gajos, Gordon McKay Professor of Computer Science.

“I love teaching,” she said. “It’s one of my favorite experiences.”

Reflecting on her time at GSD, Pillai has been deeply inspired by the faculty and her fellow students. This group from many different backgrounds with different interests and perspectives, working in many different disciplines, has been like a “dream” design studio where she’s been able to share and borrow ideas and practices from others and see how other fields look at things such as collaboration, sustainability and accessibility. It has been intellectually liberating to experience such fearlessness, she said, after years of feeling so “constrained” in her prior practice, which had been “rooted in ‘realistic goals.’”

“People tackling very huge issues that you don’t even realize 1) is a problem that could be tackled with design, and 2), they’re almost your age and they’re doing it somehow. That was very important to see,” she said.

“People really think that you can solve anything.”

Share this article

Also in this series:.

Longtime supporter of grads Kathy Hanley caps 13-year quest with a Commencement of her own

Class of ’24 gets a do-over on high school prom that pandemic took away

‘I was frustrated, infuriated, because women are just as capable’

Experiences in Uganda and U.S. fuel Ananda Birungi’s passion for empowering others, especially women and girls

You might like

Three major events, including Psychedelics Bootcamp 2024, to be hosted over summer

Epic science inside a cubic millimeter of brain

Researchers publish largest-ever dataset of neural connections

Finding right mix on campus speech policies

Legal, political scholars discuss balancing personal safety, constitutional rights, academic freedom amid roiling protests, cultural shifts

Good genes are nice, but joy is better

Harvard study, almost 80 years old, has proved that embracing community helps us live longer, and be happier

Facility for Rare Isotope Beams

At michigan state university, international research team uses wavefunction matching to solve quantum many-body problems, new approach makes calculations with realistic interactions possible.

FRIB researchers are part of an international research team solving challenging computational problems in quantum physics using a new method called wavefunction matching. The new approach has applications to fields such as nuclear physics, where it is enabling theoretical calculations of atomic nuclei that were previously not possible. The details are published in Nature (“Wavefunction matching for solving quantum many-body problems”) .

Ab initio methods and their computational challenges

An ab initio method describes a complex system by starting from a description of its elementary components and their interactions. For the case of nuclear physics, the elementary components are protons and neutrons. Some key questions that ab initio calculations can help address are the binding energies and properties of atomic nuclei not yet observed and linking nuclear structure to the underlying interactions among protons and neutrons.

Yet, some ab initio methods struggle to produce reliable calculations for systems with complex interactions. One such method is quantum Monte Carlo simulations. In quantum Monte Carlo simulations, quantities are computed using random or stochastic processes. While quantum Monte Carlo simulations can be efficient and powerful, they have a significant weakness: the sign problem. The sign problem develops when positive and negative weight contributions cancel each other out. This cancellation results in inaccurate final predictions. It is often the case that quantum Monte Carlo simulations can be performed for an approximate or simplified interaction, but the corresponding simulations for realistic interactions produce severe sign problems and are therefore not possible.

Using ‘plastic surgery’ to make calculations possible

The new wavefunction-matching approach is designed to solve such computational problems. The research team—from Gaziantep Islam Science and Technology University in Turkey; University of Bonn, Ruhr University Bochum, and Forschungszentrum Jülich in Germany; Institute for Basic Science in South Korea; South China Normal University, Sun Yat-Sen University, and Graduate School of China Academy of Engineering Physics in China; Tbilisi State University in Georgia; CEA Paris-Saclay and Université Paris-Saclay in France; and Mississippi State University and the Facility for Rare Isotope Beams (FRIB) at Michigan State University (MSU)—includes  Dean Lee , professor of physics at FRIB and in MSU’s Department of Physics and Astronomy and head of the Theoretical Nuclear Science department at FRIB, and  Yuan-Zhuo Ma , postdoctoral research associate at FRIB.

“We are often faced with the situation that we can perform calculations using a simple approximate interaction, but realistic high-fidelity interactions cause severe computational problems,” said Lee. “Wavefunction matching solves this problem by doing plastic surgery. It removes the short-distance part of the high-fidelity interaction, and replaces it with the short-distance part of an easily computable interaction.”

This transformation is done in a way that preserves all of the important properties of the original realistic interaction. Since the new wavefunctions look similar to that of the easily computable interaction, researchers can now perform calculations using the easily computable interaction and apply a standard procedure for handling small corrections called perturbation theory.  A team effort

The research team applied this new method to lattice quantum Monte Carlo simulations for light nuclei, medium-mass nuclei, neutron matter, and nuclear matter. Using precise ab initio calculations, the results closely matched real-world data on nuclear properties such as size, structure, and binding energies. Calculations that were once impossible due to the sign problem can now be performed using wavefunction matching.

“It is a fantastic project and an excellent opportunity to work with the brightest nuclear scientist s in FRIB and around the globe,” said Ma. “As a theorist , I'm also very excited about programming and conducting research on the world's most powerful exascale supercomputers, such as Frontier , which allows us to implement wavefunction matching to explore the mysteries of nuclear physics.”

While the research team focused solely on quantum Monte Carlo simulations, wavefunction matching should be useful for many different ab initio approaches, including both classical and  quantum computing calculations. The researchers at FRIB worked with collaborators at institutions in China, France, Germany, South Korea, Turkey, and United States.

“The work is the culmination of effort over many years to handle the computational problems associated with realistic high-fidelity nuclear interactions,” said Lee. “It is very satisfying to see that the computational problems are cleanly resolved with this new approach. We are grateful to all of the collaboration members who contributed to this project, in particular, the lead author, Serdar Elhatisari.”

This material is based upon work supported by the U.S. Department of Energy, the U.S. National Science Foundation, the German Research Foundation, the National Natural Science Foundation of China, the Chinese Academy of Sciences President’s International Fellowship Initiative, Volkswagen Stiftung, the European Research Council, the Scientific and Technological Research Council of Turkey, the National Natural Science Foundation of China, the National Security Academic Fund, the Rare Isotope Science Project of the Institute for Basic Science, the National Research Foundation of Korea, the Institute for Basic Science, and the Espace de Structure et de réactions Nucléaires Théorique.

Michigan State University operates the Facility for Rare Isotope Beams (FRIB) as a user facility for the U.S. Department of Energy Office of Science (DOE-SC), supporting the mission of the DOE-SC Office of Nuclear Physics. Hosting what is designed to be the most powerful heavy-ion accelerator, FRIB enables scientists to make discoveries about the properties of rare isotopes in order to better understand the physics of nuclei, nuclear astrophysics, fundamental interactions, and applications for society, including in medicine, homeland security, and industry.

The U.S. Department of Energy Office of Science is the single largest supporter of basic research in the physical sciences in the United States and is working to address some of today’s most pressing challenges. For more information, visit energy.gov/science.